Sprawdź się
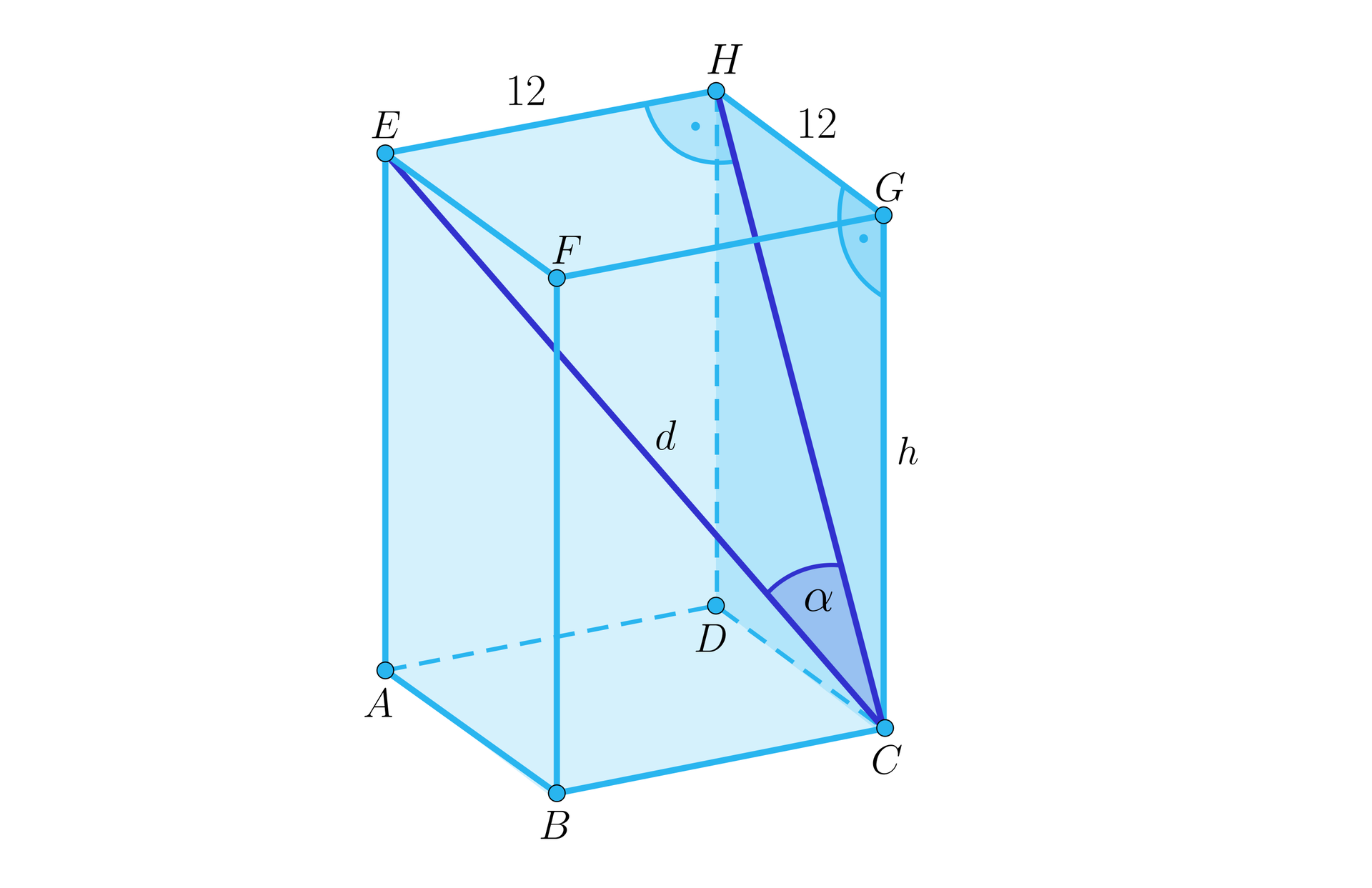
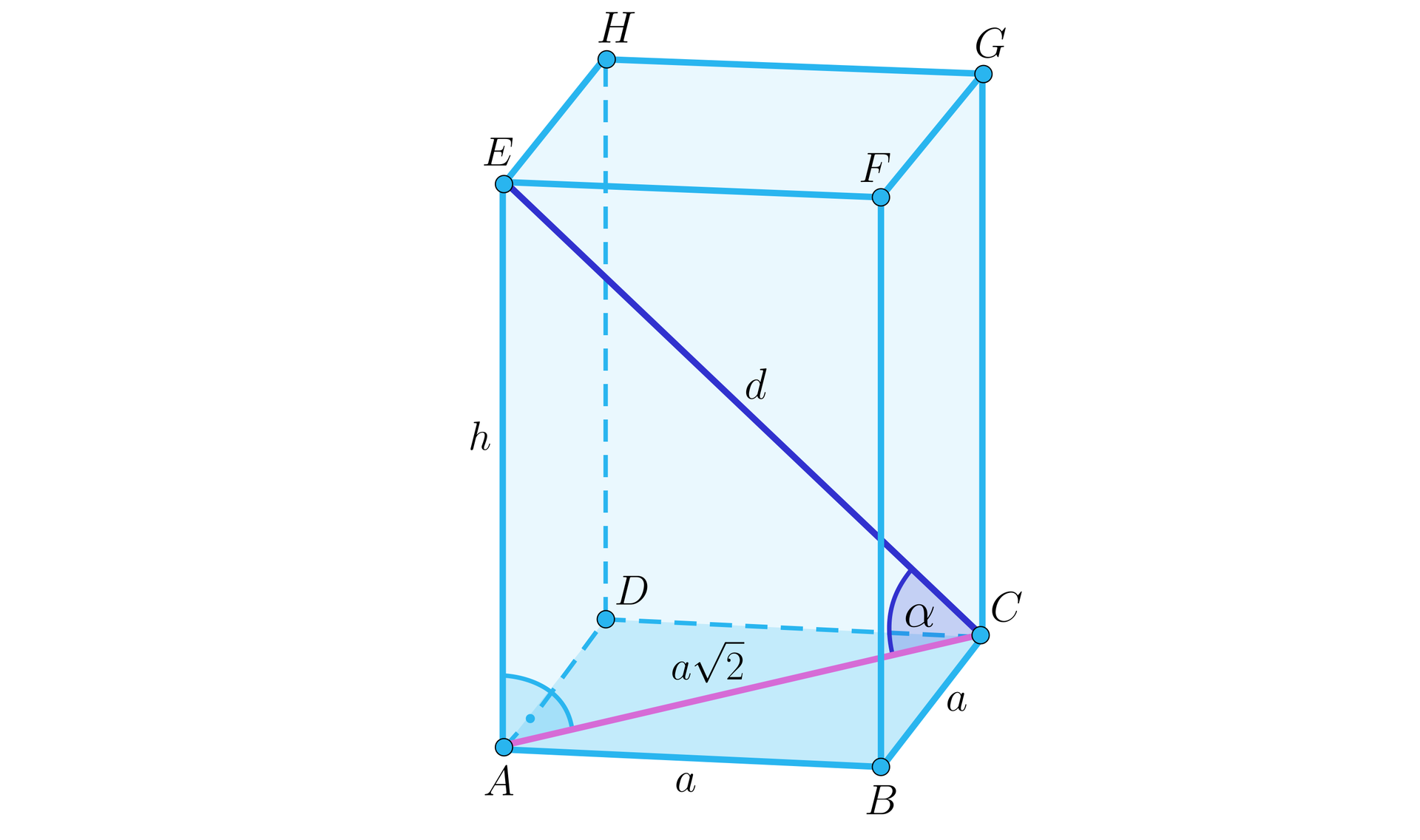
Kąt nachylenia przekątnej graniastosłupa prawidłowego czworokątnego do płaszczyzny ściany bocznej to kąt pomiędzy 1. przekątną graniastosłupa a przekątną podstawy, 2. przekątną graniastosłupa a przekątną ściany bocznej.
Uzupełnij tekst.
przekątną ściany bocznej a krawędzią boczną, przekątną graniastosłupa a przekątną ściany bocznej, przekątną graniastosłupa a przekątną podstawy, przekątną graniastosłupa a krawędzią podstawy
Kąt nachylenia przekątnej graniastosłupa prawidłowego czworokątnego do płaszczyzny podstawy to kąt pomiędzy .....................................................................................................................
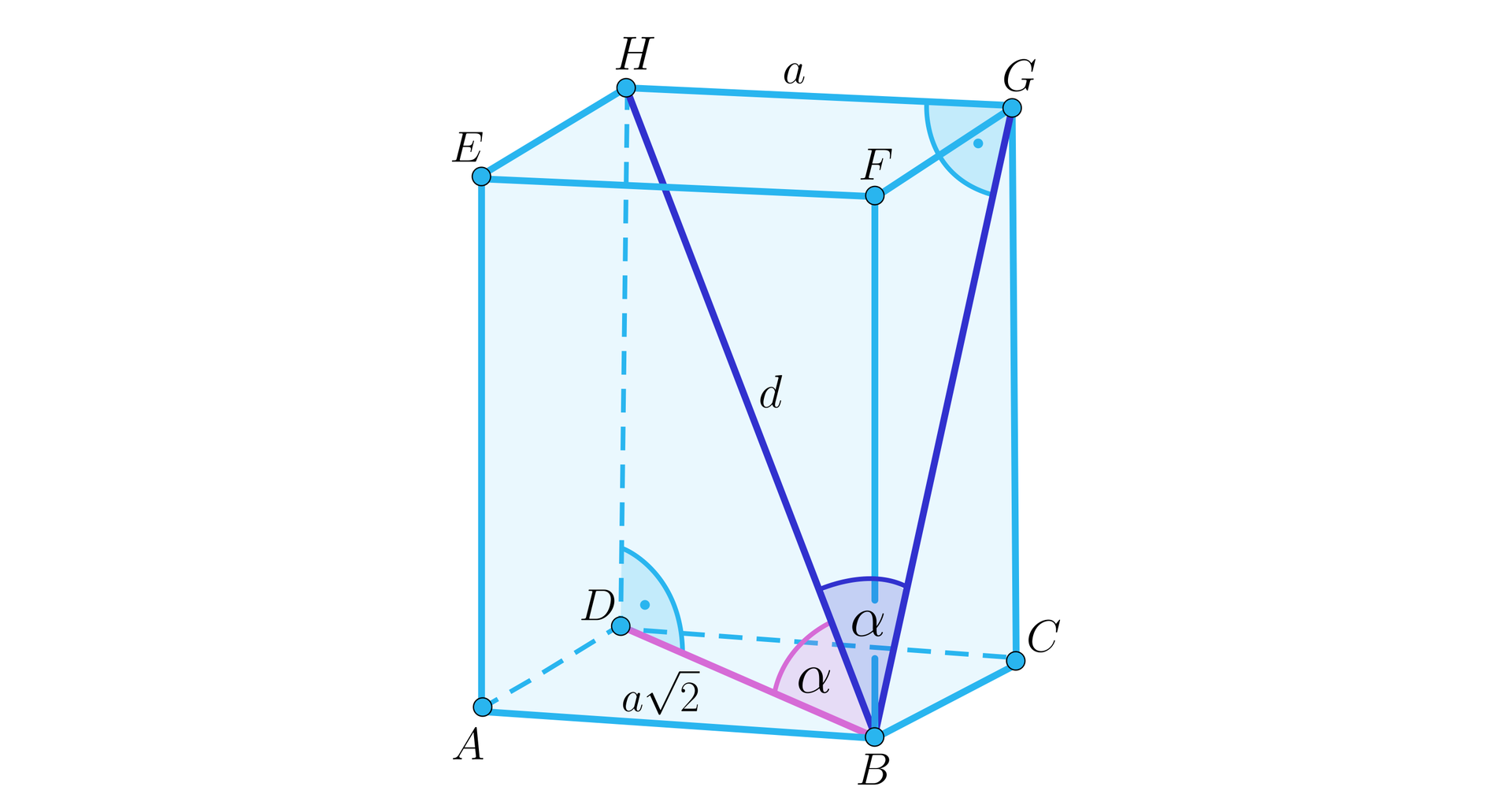
Kąt nachylenia przekątnej graniastosłupa prawidłowego czworokątnego do płaszczyzny ściany bocznej to kąt pomiędzy .....................................................................................................................
W graniastosłupie prawidłowym czworokątnym krawędź boczna jest trzy razy dłuższa od krawędzi podstawy. Cosinus kąta między przekątną ściany tego graniastosłupa a płaszczyzną podstawy wynosi:
W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość , a kąt nachylenia przekątnej do płaszczyzny podstawy jest równy . Suma długości wszystkich krawędzi tego graniastosłupa jest równa:
Długość krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa . Przekątna tego graniastosłupa jest nachylona do płaszczyzny ściany bocznej pod kątem, którego cosinus jest równy . Oblicz długość krawędzi bocznej tego graniastosłupa.
Dany jest graniastosłup prawidłowy czworokątny o długości krawędzi bocznej . Suma pola kwadratu w podstawie oraz pola prostokąta będącego ścianą boczną wynosi . Czy kąt nachylenia przekątnej tego graniastosłupa do płaszczyzny podstawy jest większy niż ? Odpowiedź uzasadnij.
Wyznacz sinus kąta nachylenia prostej do płaszczyzny podstawy w sześcianie, którego rysunek widzisz poniżej, wiedząc, że punkt jest środkiem krawędzi .
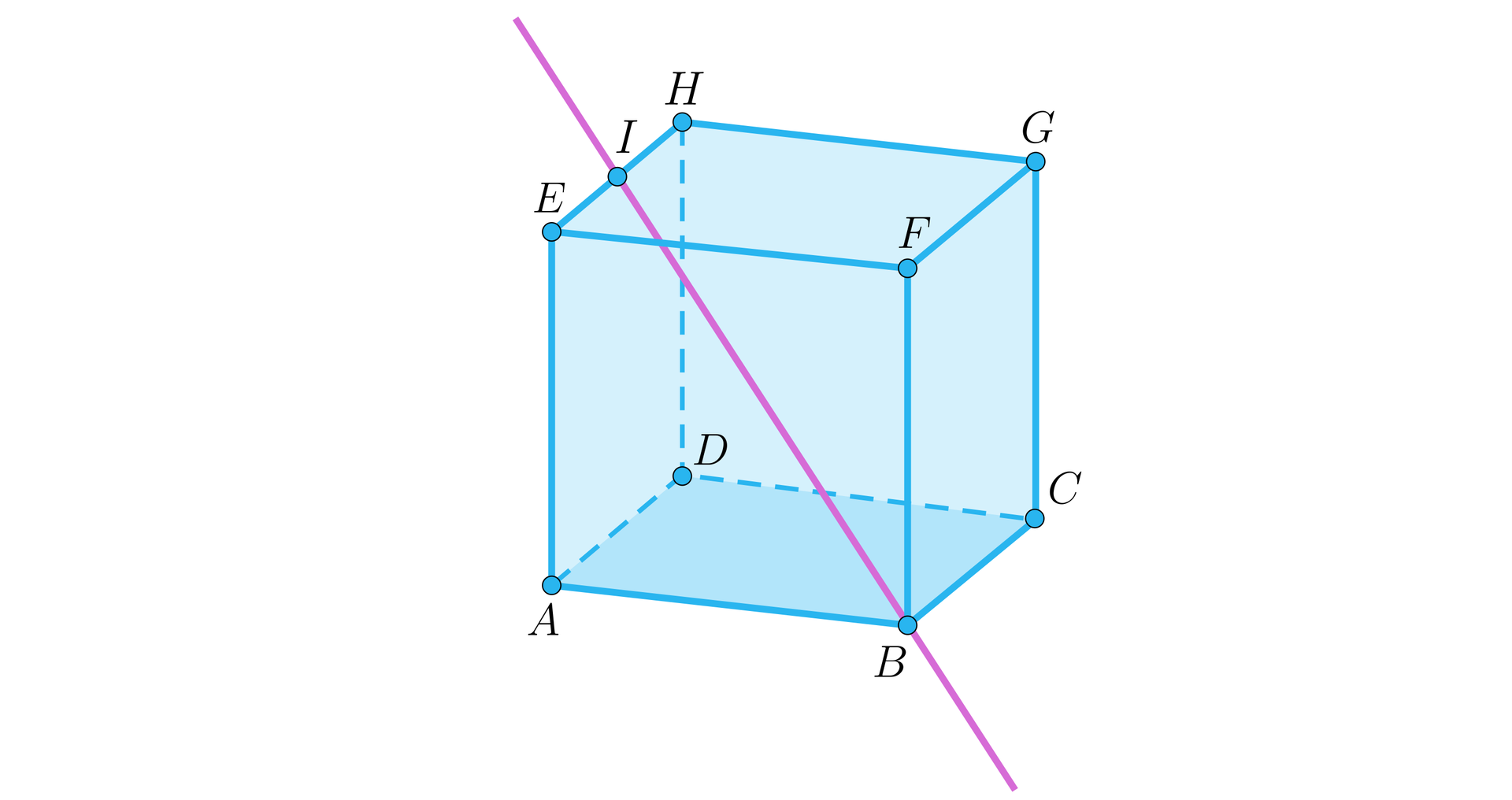
W graniastosłupie prawidłowym czworokątnym kąt nachylenia przekątnej graniastosłupa do płaszczyzny podstawy ma taką samą miarę jak kąt nachylenia przekątnej graniastosłupa do płaszczyzny ściany bocznej. Wyznacz tangens i przybliżoną miarę tego kąta.