Proporcjonalność odwrotna
W rozdziale o funkcjach omówione zostały zależności wprost proporcjonalne. Teraz zajmiemy się wielkościami odwrotnie proporcjonalnymi.
Szkoła przeznaczyła kwotę na wydruk ulotek promocyjnych. Ceny proponowane za usługę wydruku tej samej ulotki w różnych drukarniach zebrano w tabeli.
cena wydruku ulotki (p) [zł] | ||||||||
liczba ulotek () [szt] |
Za każdym razem koszt wydruku wszystkich ulotek jest taki sam: .
Zauważmy, że im wyższa cena jednostkowa wydruku, tym mniej ulotek możemy wydrukować za podaną kwotę.
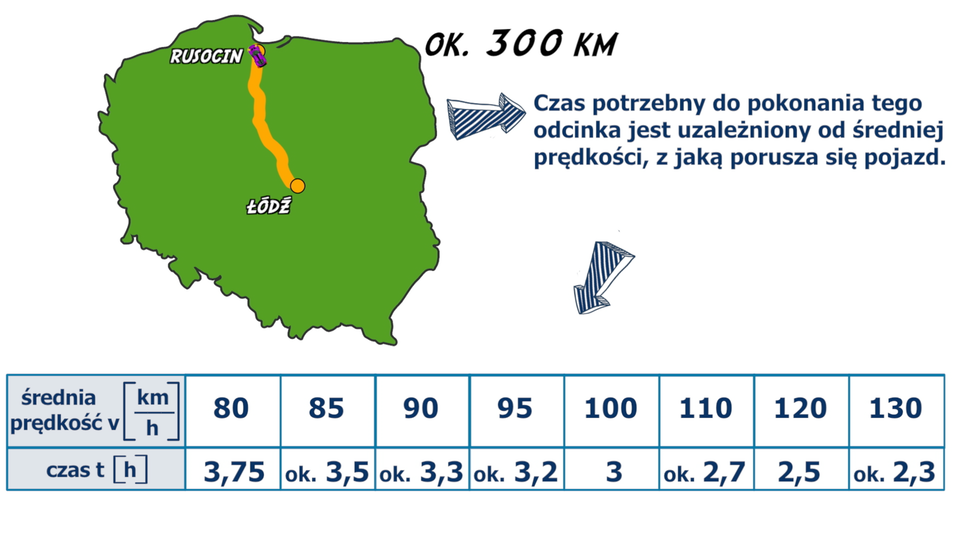
Długość oddanej do użytku (do roku) autostrady od węzła Łódź Północ (woj. łódzkie) do węzła Rusocin (woj. pomorskie) to ok. . Czas potrzebny na przejazd tego odcinka jest uzależniony od średniej prędkości, z jaką porusza się pojazd. Zależności między tymi wielkościami przedstawia tabela.
średnia prędkość | ||||||||
czas przejazdu | ok. | ok. | ok. | ok. | ok. |
Zauważmy, że jeśli zwiększa się średnia prędkość samochodu , to czas przejazdu jest coraz krótszy.
Film dostępny na portalu epodreczniki.pl
Animacja prezentuje samochód poruszający się po drodze zaznaczonej na mapie Polski. Długość oddanej do użytku (do 2015 roku) autostrady A1 od węzła Łódź Północ (woj. łódzkie) do węzła Rusocin (woj. pomorskie) to ok. 300 km. Czas przejazdu tego odcinka jest uzależniony od średniej prędkości v, z jaką porusza się pojazd. v =80 kilometrów na godzinę, to czas przejazdu t = 3,75 godziny, v =85 kilometrów na godzinę, to czas przejazdu t około 3,5 godziny, v =90 kilometrów na godzinę, to czas przejazdu t około 3,3 godziny, v =95 kilometrów na godzinę, to czas przejazdu t około 3,2 godziny, v =100 kilometrów na godzinę, to czas przejazdu t = 3 godziny, v =110 kilometrów na godzinę, to czas przejazdu t około 2,7 godziny, v =120 kilometrów na godzinę, to czas przejazdu t =2,5 godziny, v =130 kilometrów na godzinę, to czas przejazdu t około 2,3 godziny. Zauważmy, że jeśli zwiększa się średnia prędkość samochodu ( v), to czas przejazdu ( t) jest coraz krótszy.
Rozpatrzmy wszystkie prostokąty o bokach , których pole jest równe .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DcN2NwaMD
Pola prostokątów są równe . Iloczyn jest stały, a zwiększenie długości jednego z boków powoduje proporcjonalne zmniejszenie długości drugiego boku.
Wielkości przedstawione w powyższych przykładach charakteryzują się tym, że wzrost jednej z nich powoduje takie zmniejszenie drugiej, że iloczyn tych wielkości pozostaje stały. O takich wielkościach będziemy mówić, że są odwrotnie proporcjonalne.
Mówimy, że dwie dodatnie wielkości i są odwrotnie proporcjonalne wtedy i tylko wtedy, gdy ich iloczyn jest stały i różny od zera.
Funkcja opisująca zależność między dodatnimi wielkościami odwrotnie proporcjonalnymi i nazywana jest proporcjonalnością odwrotną, a iloczyn nazywany jest współczynnikiem proporcjonalności odwrotnej.
Z faktu, że liczby i są dodatnie, wynika, że współczynnik także jest dodatni.
Zależność między wielkościami odwrotnie proporcjonalnymi i możemy zapisać również w postaci .