Przeczytaj

Na początek omówimy własności równoległoboku.

Na rysunku przedstawiony jest równoległobokrównoległobokrównoległobok $A B C D$ z zaznaczonymi przekątnymi i kątami. Oznaczenia z tego rysunku wykorzystamy do opisu własności.

Zastosujemy oznaczenie $d_{1}$ na przekątną $A C$ oraz $d_{2}$ na przekątną $B D$ . Ponadto, niech $h_{a}$ oznacza wysokość równoległoboku opuszczoną na bok $a$ i niech $h_{b}$ oznacza wysokość równoległoboku opuszczoną na bok $b$ .

R1MoU4CoR3svu

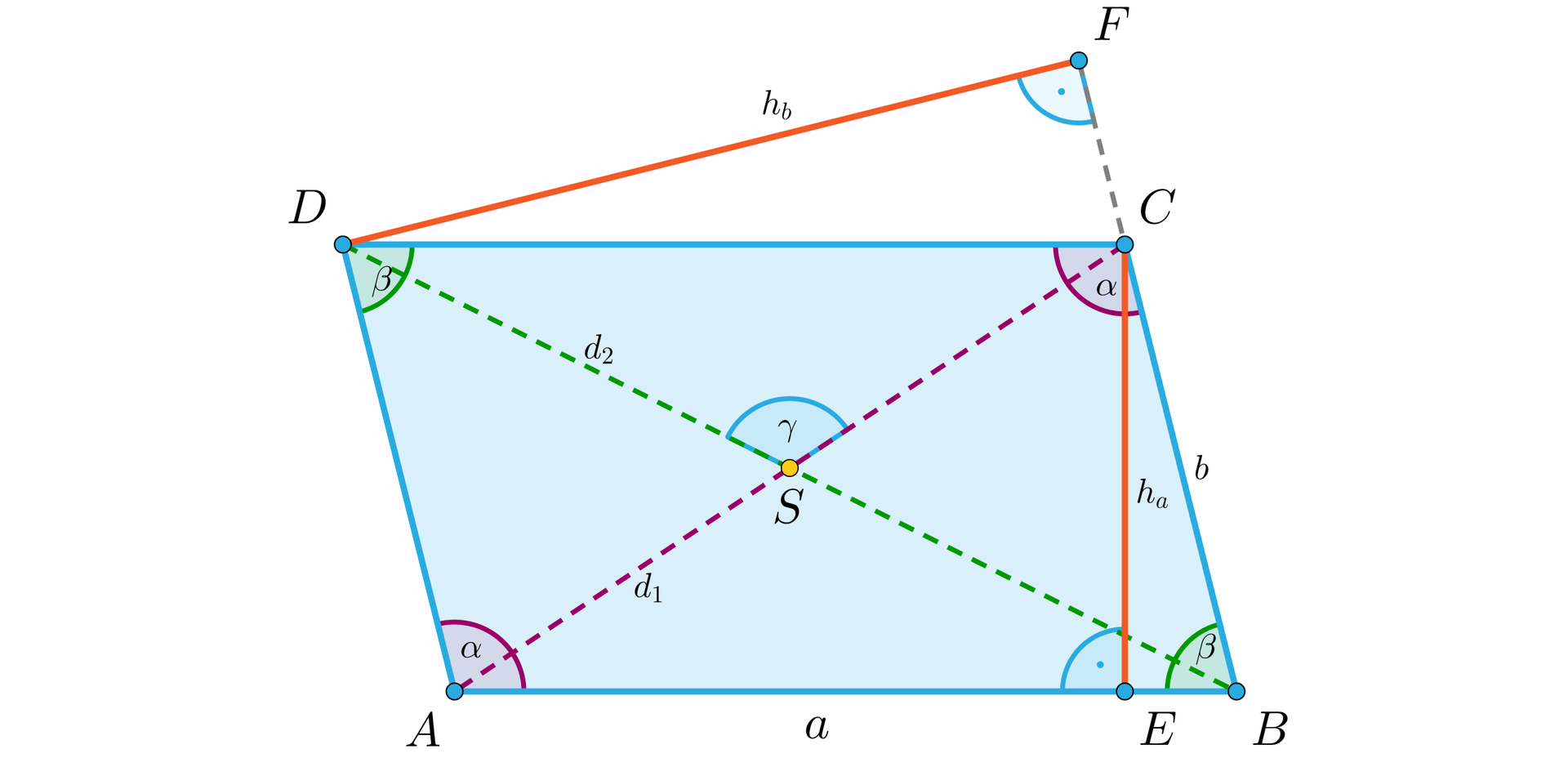
Własności równoległoboku

Równoległobok ma dwie pary boków równoległych: $D C ∥ A B$ , $B C ∥ A D$ .

Boki równoległe mają równe długości: $|D C| = |A B| = a$ , $|A D| = |B C| = b$ .

Kąty przeciwległe mają równe miary: $∢ B A D = ∢ B C D = α$ , $∢ A B C = ∢ A D C = β$ .

Suma kątów sąsiednich jest równa $180 °$ : $α + β = 180^{\circ}$ .

Przekątne przecinają się w połowie: $|A S| = |S C| = \frac{|A C|}{2} = \frac{d_{1}}{2}$ , $|B S| = |S D| = \frac{|B D|}{2} = \frac{d_{2}}{2}$ .

Własności kątów pod jakimi przecinają się przekątne: $∢ C S D = ∢ A S B = γ$ , $∢ A S D = ∢ B S C = 180^{\circ} - γ$ .

Z własności funkcji sinussinus wnioskujemy: $\sin γ = \sin (180 ° - γ)$ oraz $\sin α = \sin β$ .

Załóżmy, że potrafimy wyliczyć pole trójkąta. Pokażemy jak wtedy wyznaczyć pole równoległoboku.

Każda przekątna dzieli równoległobok $A B C D$ na dwa przystające trójkąty na mocy cechy $b - k - b$ : $A B C$ przystaje do $C D A$ oraz $B A D$ do $B C D$ .

Stąd pole równoległoboku jest dwa razy większe niż pole jednego z tych trójkątów.

Z powyższych rozważań wyciągniemy wniosek, że dwa trójkąty, które mają boki $a$ i $b$ , gdzie w pierwszym trójkacie kąt między bokami wynosi $α$ , w drugim $β$ spełniają zależność $α = 180 ° - β$ mają równe pola.

Rzeczywiście, pole trójkąta $A B C$ jest równe połowie pola równoległoboku, podobnie pole trójkąta $B C D$ jest równe połowie pola równoległoboku.

Trójkąt $A B C$ ma boki $a$ , $b$ i kąt między tymi bokami równy $β$ , natomiast trójkąt $B C D$ ma również boki $a$ , $b$ a kąt między tymi bokami równy $α$ . Z własności $4$ , $α + β = 180 °$ .

pole równoległoboku 1

Twierdzenie: pole równoległoboku 1

Pole równoległoboku jest równe

P = a \cdot h_{a}

gdzie $a$ jest dowolnym bokiem równoległoboku, a $h_{a}$ jest wysokością spuszczoną na ten bok.

Dowód

Niech $E^{'}$ będzie punktem przecięcia prostej poprowadzonej z wierzchołka $D$ równoległej do wysokości z prostą zawierająca bok $A B$ . Wtedy czworokąt $D C E E^{'}$ jest prostokątem o polu równym $|D C| \cdot |C E| = a \cdot h_{a}$ .

RFzvgGWTSzarS

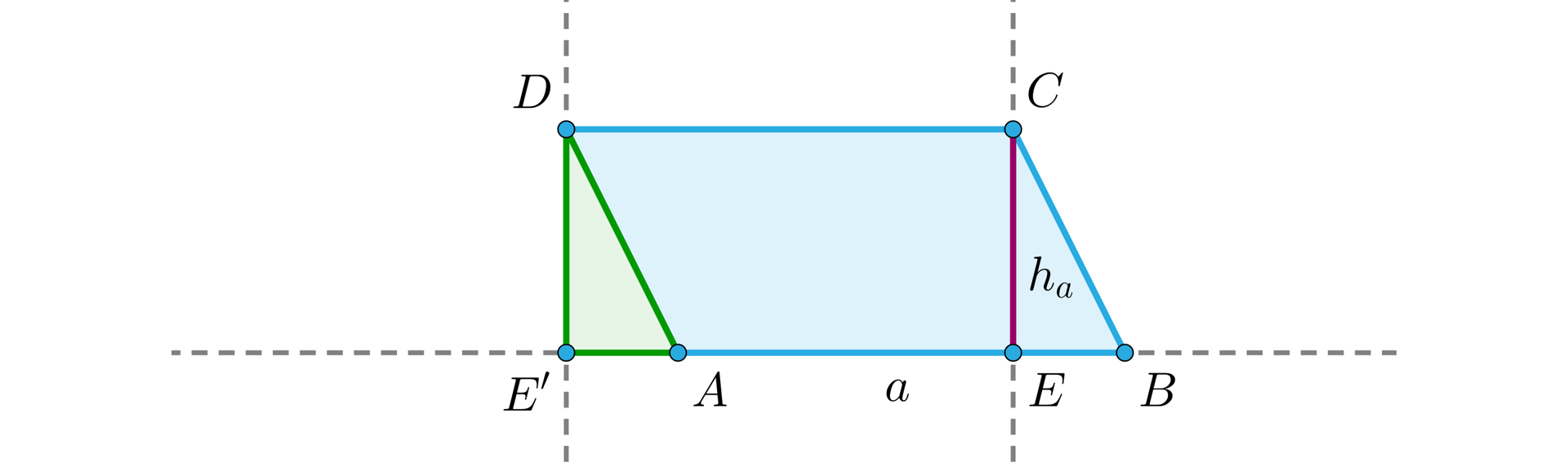
Trójkąty $B C E$ i $A D E^{'}$ są przystające na mocy cechy przystawania $b - k - b$ .

Stąd pole równoległoboku $P = P_{A E C D} + P_{B C E} = P_{A E C D} + P_{A D E^{'}} = a \cdot h_{a}$ .

Przykład 1

Jedna z wysokości w równoległoboku o polu $10$ ma długość $2$ , druga z wysokości ma długość $4$ . Wyznaczymy długości boków.

Rozwiązanie

$a \cdot h_{a} = a \cdot 2 = 10$ , więc $a = 5$

$b \cdot h_{b} = b \cdot 4 = 10$ , więc $b = 2, 5$

Zatem równoległobok ma boki długości $5$ i $2, 5$ .

W dowodzie twierdzenia sprowadziliśmy zadanie policzenia pola równoległoboku do wyznaczenia pola prostokąta. Pokażemy jeden ze sposobów sprowadzenia zadania policzenia pola równoległoboku do wyznaczenia pola trójkąta.

Przykład 2

Niech $A B C D$ będzie równoległobokiem. Na prostej $B C$ zaznaczamy punkt $B^{'}$ taki, że $|B C| = |C B^{'}|$ . Wykażemy, że pole równoległoboku $A B C D$ jest równe polu trójkąta $A B B^{'}$ .

R14aoGkHhpV79

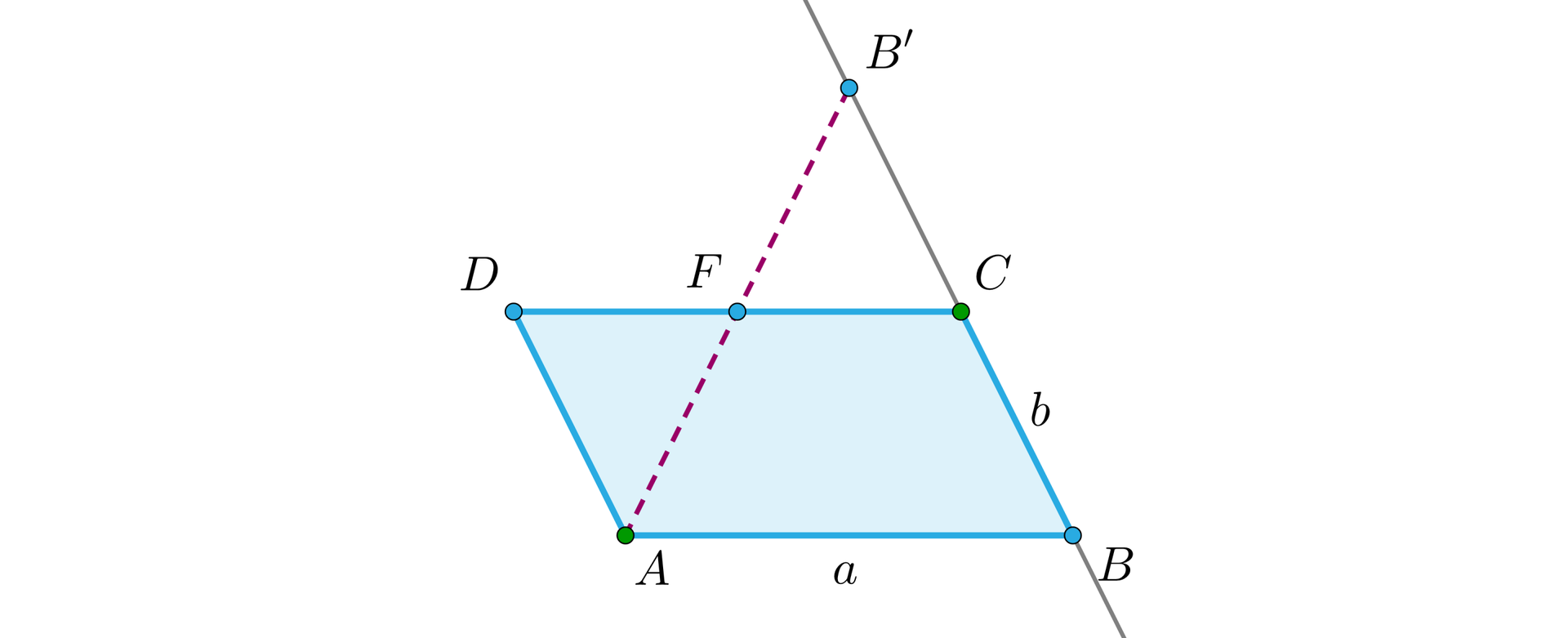
Rozwiązanie

Prowadzimy odcinek $B^{'} A$ . Niech punkt $F$ będzie punktem przecięcia odcinka $A B^{'}$ z bokiem $D C$ .

Wtedy, z twierdzenia Talesa wynika, że $|C F| = \frac{|A B|}{2}$ oraz z twierdzenia odwrotnego do twierdzenia Talesa mamy, że trójkąty $C F B^{'}$ i $D F A$ są przystające.

Stąd wynika, że pole równoległoboku $A B C D$ jest równe polu trójkąta $A B B^{'}$ .

pole równoległoboku 2

Twierdzenie: pole równoległoboku 2

Pole równoległoboku o bokach $a$ , $b$ i kącie $α$ między tymi bokami jest równe

P = a b \sin α

Dowód

Pole równoległoboku $A B C D$ jest równe $P = 2 P_{B A D} = 2 \cdot \frac{a b \sin α}{2} = a b \sin α$ .

Prostokąt jest równoległobokiem, więc jego pole jest równe $P = a b \sin α = a b \sin 90^{\circ} = a b$ .

Przykład 3

Kąt między dwoma bokami równoległoboku o długościach $5 cm$ i $6 cm$ ma miarę równą $30 °$ . Wyznaczymy pole tego równoległoboku.

Rozwiązanie

Obliczymy pole tego równoległoboku podstawiając bezpośrednio do wzoru:

$P = 5 \cdot 6 \cdot \sin 30 ° = 30 \cdot \frac{1}{2} = 15$

pole równoległoboku 3

Twierdzenie: pole równoległoboku 3

Pole równoległoboku o przekątnych $d_{1}$ , $d_{2}$ i kącie $γ$ między przekątnymi jest równe

P = \frac{d_{1} \cdot d_{2}}{2} \sin γ

Dowód

Ry1pqN3Qe9Pav

Pole równoległoboku $A B C D$ jest równe:

$P = P_{A S B} + P_{C S D} + P_{A S D} + P_{C S B} = 2 P_{A S B} + 2 P_{A S D} =$

$= 2 \cdot \frac{\frac{d_{1}}{2} \cdot \frac{d_{2}}{2}}{2} \sin γ + 2 \frac{\frac{d_{1}}{2} \cdot \frac{d_{2}}{2}}{2} \sin (180 ° - γ) = \frac{d_{1} \cdot d_{2}}{4} (\sin γ + \sin (180 ° - γ)) =$

$= \frac{d_{1} \cdot d_{2}}{4} \cdot 2 \cdot \sin γ = \frac{d_{1} \cdot d_{2}}{2} \sin γ$

Przykład 4

Przekątne równoległoboku mają długości $14$ i $18$ , a kąt rozwarty między przekątnymi jest $5$ razy większy niż kąt ostry. Wyznaczymy pole tego równoległoboku.

Rozwiązanie

Niech $α$ będzie miarą kąta ostrego. Wtedy $α + 5 α = 180 °$ , więc $α = \frac{180 °}{6} = 30 °$ .

Zatem $P = \frac{14 \cdot 18}{2} \cdot \sin 30^{\circ} = \frac{14 \cdot 18}{2 \cdot 2} = 63$ .

Zanim podamy kolejny wzór na pole równoległoboku przypomnimy, że dwa niezerowe wektory $[a_{x}, a_{y}]$ , $[b_{x}, b_{y}]$ zaczepione we wspólnym początku wyznaczają równoległobok oraz że niezależnie od punktu zaczepienia, równoległoboki rozpięte na danych wektorach są przystające. Stąd wynika, że do obliczenia pola równoległoboku można zaczepić wektory w początku układu współrzędnych.

pole równoległoboku 4

Twierdzenie: pole równoległoboku 4

Pole P równoległoboku wyznaczonego przez dwa niezerowe wektory $[a_{x}, a_{y}]$ , $[b_{x}, b_{y}]$ zaczepione we wspólnym początku jest równe

P = |a_{x} b_{y} - a_{y} b_{x}|

Zamiast dowodu popatrzmy na rysunek:

Na rysunku przedstawiony jest równoległobok $A B D C$ rozpięty na wektorach $A C = [a_{x}, a_{y}]$ , i $A B = [b_{x}, b_{y}]$ .

RZBpizqR8YMeV

Wtedy pole równoległoboku jest równe polu prostokątaprostokątprostokąta $A E F G$ pomniejszonego o pole prostokąta $F H D I$ , co widać na rysunku.

$P_{A E F G} = |A G| \cdot |A E| = a_{x} \cdot b_{y}$ , $P_{F H D I} = |F I| \cdot |F H| = a_{y} \cdot b_{x}$

Zatem pole równoległoboku jest równe $P = a_{x} b_{y} - a_{y} b_{x}$ .

Może się też zdarzyć, że $a_{x} b_{y} - a_{y} b_{x}$ będzie liczbą ujemną i wtedy $P = |a_{x} b_{y} - a_{y} b_{x}|$ .

Przykład 5

Na wcześniejszym rysunku wektor $A C$ ma współrzędne $[2, 3]$ , a wektor $A B$ ma współrzędne $[7, 2]$ . Obliczymy, ile wynosi pole równoległoboku rozpiętego na tych wektorach.

Rozwiązanie

Pole równoległoboku rozpiętego na tych wektorach wynosi $P = 3 \cdot 7 - 2 \cdot 2 = 17$ .

Zastosowania

Przykład 6

Pokażemy, jak wyznaczyć pole trapezu znając pole równoległoboku.

Na rysunku mamy trapez $A B C D$ o podstawach $a$ i $b$ oraz wysokości $h$ , dla którego przedstawimy dwie metody obliczenia pola.

R1Dc6whiMN6Tu

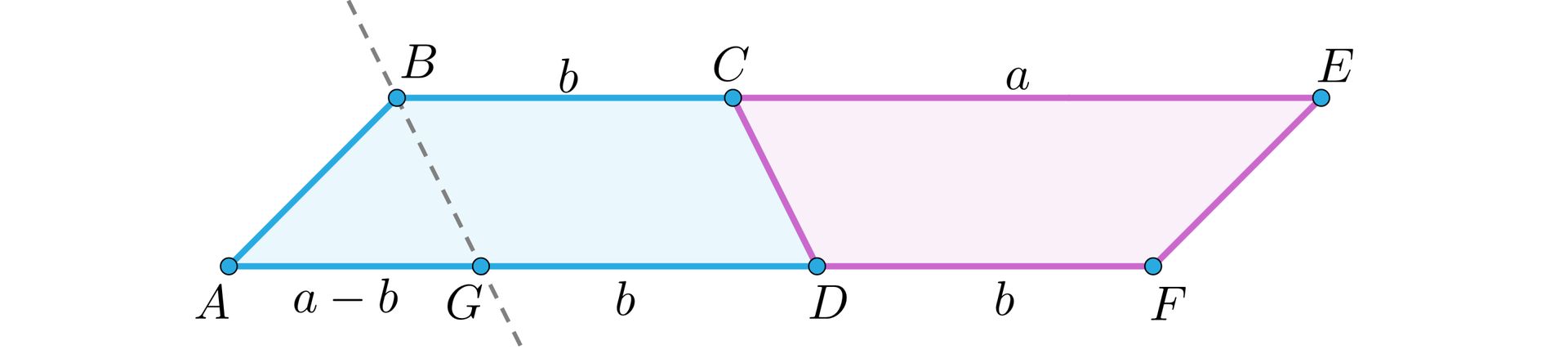
Rozwiązanie

Metoda pierwsza polega na dorysowaniu do trapezu drugiego przystającego do niego trapezu (różowy). Wtedy powstaje równoległobok o tej samej wysokości co wysokość trapezu i o boku równym $a + b$ . Pole trapezu jest dwa razy mniejsze od pola tego równoległoboku, czyli pole trapezu wynosi:

P = \frac{1}{2} (a + b) \cdot h

W metodzie drugiej prowadzimy z dowolnego wierzchołka przy krótszej podstawie prostą równoległą do drugiego ramienia. Prosta ta dzieli trapez na równoległobok o wysokości $h$ i boku $b$ oraz trójkąt o wysokości $h$ i podstawie $a - b$ . Wtedy pole trapezu wynosi:

P = \frac{1}{2} (a - b) \cdot h + b \cdot h = h (\frac{a}{2} - \frac{b}{2} + b) = h (\frac{a}{2} + \frac{b}{2}) = \frac{1}{2} (a + b) \cdot h

Przykład 7

Znane jest twierdzenie, że w dowolnym czworokącie wypukłym czworokąt, którego wierzchołkami są środki jego boków jest równoległobokiem. Pokażemy, że pole tego równoległoboku jest połową pola $P$ tego czworokąta.

Rozwiązanie

Na rysunku widać czworokąt $A B C D$ i czworokąt $E F G H$ , który łączy środki boków.

RxXymPJKkUz0N

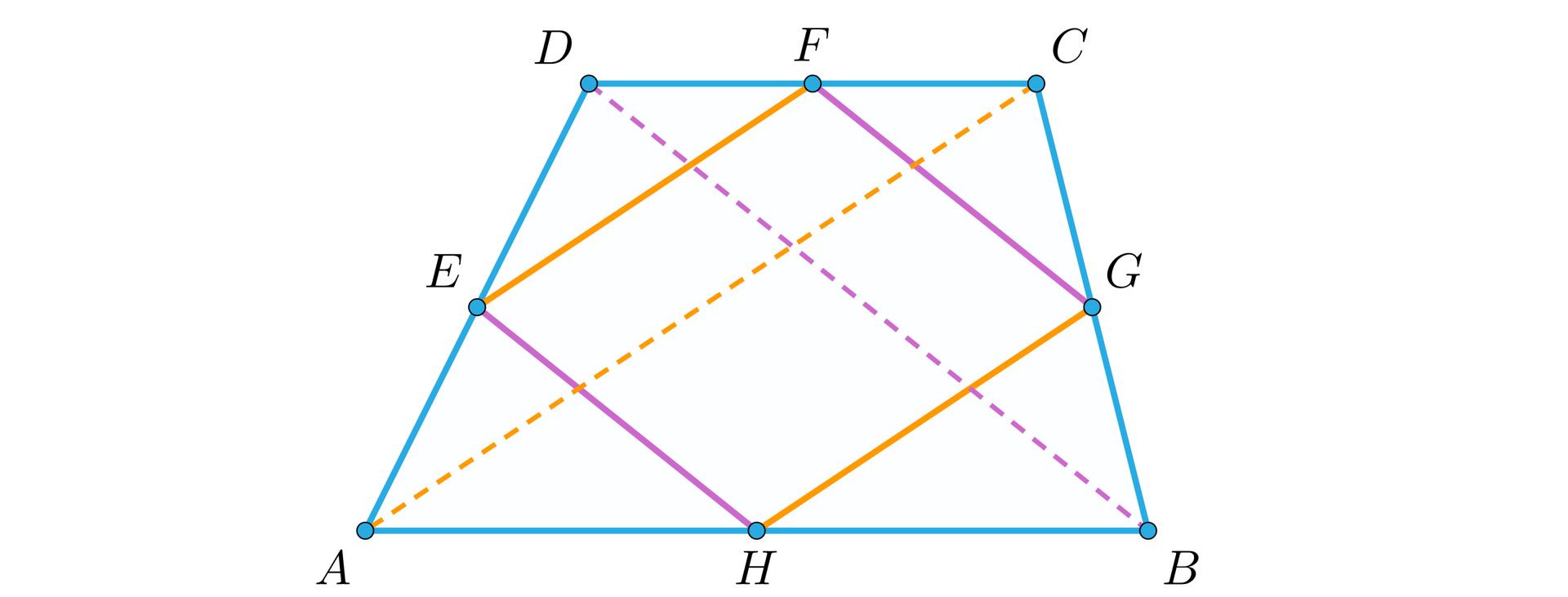
Z własności linii środkowej w trójkątach $B C D$ i $B A D$ wynika, że boki $F G$ i $E H$ są równoległe do przekątnej $B D$ i mają długość równą połowie długości tej przekątnej.

Stąd też wynika, że $P_{H A E} = \frac{1}{4} P_{B A D}$ i $P_{G C F} = \frac{1}{4} P_{B C D}$ .

Analogiczne rozważania prowadzą do wniosku, że $P_{E D F} = \frac{1}{4} P_{A D C}$ i $P_{H B G} = \frac{1}{4} P_{A B C}$

Teraz zauważamy, że pole równoległoboku wynosi $P_{E F G H} = P - (P_{H A E} + P_{G C F} + P_{E D F} + P_{H B G})$

Z drugiej strony wiemy, że $P = P_{B A D} + P_{B C D} = P_{A D C} + P_{A B C}$ , więc:

$2 P = P_{B A D} + P_{B C D} + P_{A D C} + P_{A B C} = 4 P_{H A E} + 4 P_{G C F} + 4 P_{E D F} + 4 P_{H B G}$

Stąd $P_{H A E} + P_{G C F} + P_{E D F} + P_{H B G} = \frac{P}{2}$

Ostatecznie, $P_{E F G H} = P - \frac{P}{2} = \frac{P}{2}$

Zatem pole równoległoboku $E F G H$ jest połową pola czworokąta $A B C D$ .

Słownik

równoległobok

czworokąt, który ma dwie pary boków równoległych

prostokąt

czworokąt, który ma wszystkie kąty proste

sinus kąta w trójkącie prostokątnym

stosunek długości przyprostokątnej leżącej naprzeciw kąta i długości przeciwprostokątnej

Wprowadzenie

Symulacja interaktywna

Własności równoległoboku

Zastosowania

Słownik