O innych okręgach wpisanych w czworokąt

Rozważmy czworokąt wypukły $ABCD$ i poprowadźmy jego przekątną $BD$. Rozważmy okręgi wpisane odpowiednio w trójkąt $ABD$ i w trójkąt $BCD$, jak na rysunku.

R1QEOVvocPKiq

Ilustracja przedstawia czworokąt ABCD który podzielono przekątną DB na dwa trójkąty ABD i BCD. W oba trójkąty wpisano okręgi , jeden w trójkącie ABD styka się z przekątną DB w punkcie P a drugi w trójkącie BCD styka się z przekątną w punkcie Q.

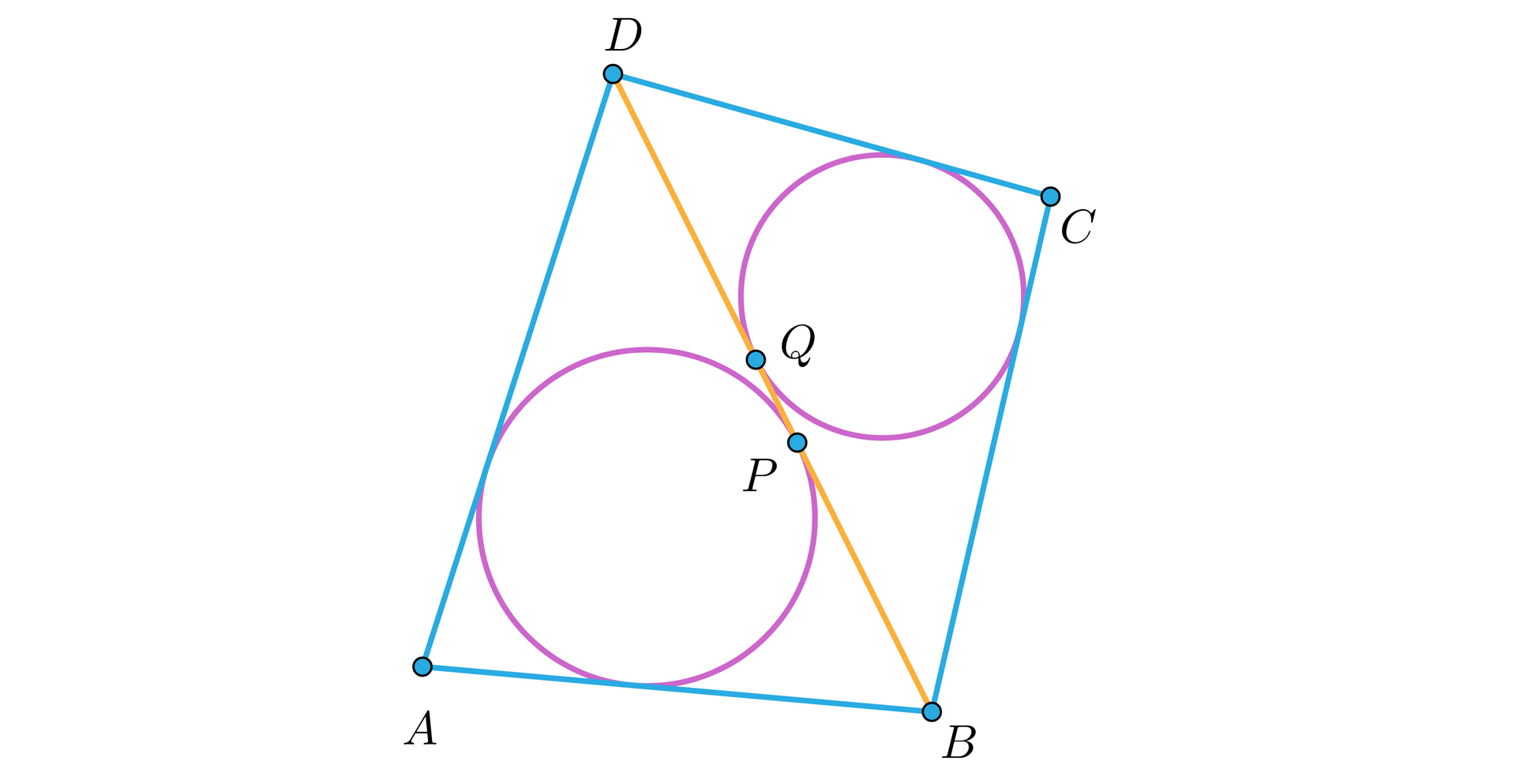
Okręgi te są styczne do przekątnej $BD$ odpowiednio w punktach $P$ i $Q$.

Prawdziwe jest wówczas następujące twierdzenie.

O okręgach wpisanych w czworokąt

Twierdzenie: O okręgach wpisanych w czworokąt

Rozważmy czworokąt wypukły $ABCD$. Niech $P$ będzie punktem, w którym okrąg wpisany w trójkąt $ABD$ jest styczny do przekątnej $BD$. Niech $Q$ będzie punktem, w którym okrąg wpisany w trójkąt $BCD$ jest styczny do przekątnej $BD$. Jeśli punkty $P$ i $Q$ się pokrywają, to w czworokąt $ABCD$ można wpisać okrąg.

Dowód

Niech punkty $E$, $F$, $G$, $H$ będą punktami, w których odpowiednie okręgi są styczne do boków czworokąta, jak na rysunku.

R1Gn0wFNhxbWN

Ilustracja przedstawia czworokąt ABCD który podzielono przekątną DB na dwa trójkąty ABD i BCD. W oba trójkąty wpisano okręgi , jeden w trójkącie ABD styka się z nim w punktach H i E oraz przekątną DB w punkcie P  a drugi w trójkącie BCD styka się z nim w punkach G i F oraz przekątną w punkcie Q. Punkt P pokrywa się z punktem Q.

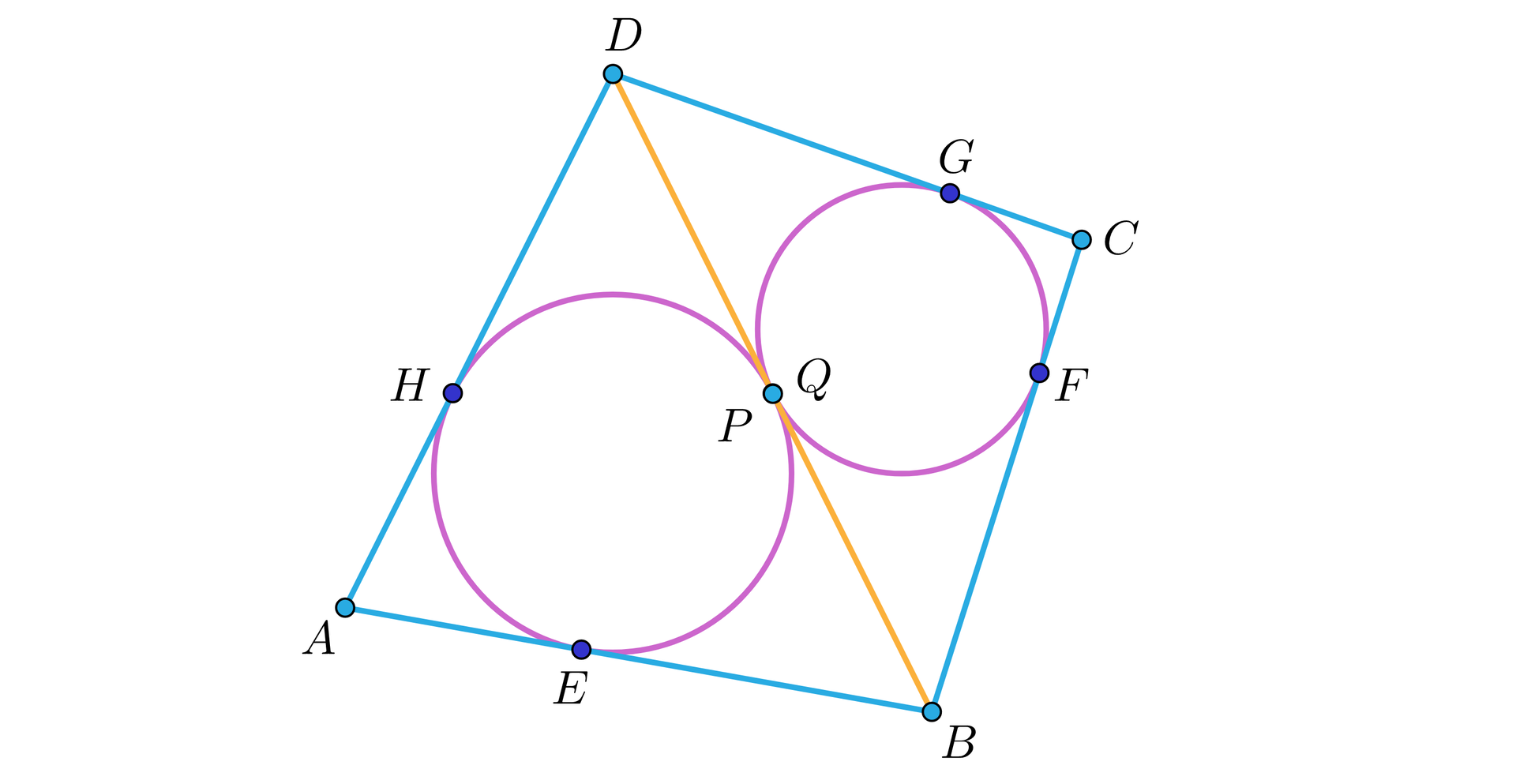
Zauważmy, że korzystając z zasadniczego twierdzenia planimetrii mamy, że

$\left|AB\right|+\left|CD\right|=\left|AE\right|+\left|EB\right|+\left|CG\right|+\left|GD\right|=$

$=\left|AH\right|+\left|BP\right|+\left|CF\right|+\left|DQ\right|=$

$=\left|AH\right|+\left|BF\right|+\left|CF\right|+\left|DH\right|=\left|AD\right|+\left|BC\right|$

Na mocy warunku koniecznego i wystarczającego na to, by w czworokąt dało się wpisać okrąg, otrzymujemy, że w czworokąt $ABCD$ można wpisać okrąg. Co kończy dowód.

Warto nadmienić, że prawdziwe jest także twierdzenie odwrotne, co oznacza, że otrzymaliśmy kolejne kryterium pozwalające rozstrzygnąć, czy w dany czworokąt można wpisać okrąg.

O polu trapezu równoramiennego, w który można wpisać okrąg

Wrócimy teraz do przywołanego na wstępie twierdzenia, które wyraża pole czworokąta poprzez pierwiastek kwadratowy z iloczynu jego boków. Pominiemy w tym miejscu dowód w przypadku ogólnym, ale pokażemy w łatwy sposób, że wzór ten jest prawdziwy dla trapezów równoramiennych opisanych na okręgu.

Rozważmy zatem trapeztrapeztrapez równoramienny $ABCD$, w który można wpisać okrąg i przyjmijmy oznaczenia, jak na rysunku.

R1ILLqN11kvg8

Ilustracja przedstawia trapez równoramienny ABCD w który wpisano okrąg. Dłuższa podstawa trapezu ma długość a , krótsza długość b a boki mają długość c. Wysokość trapezu została opuszczona z punktu C do punktu F dzielącego podstawę AB na odcinki AF i FB . Odcinek FB ma długość $\frac{a-b}{2}$.

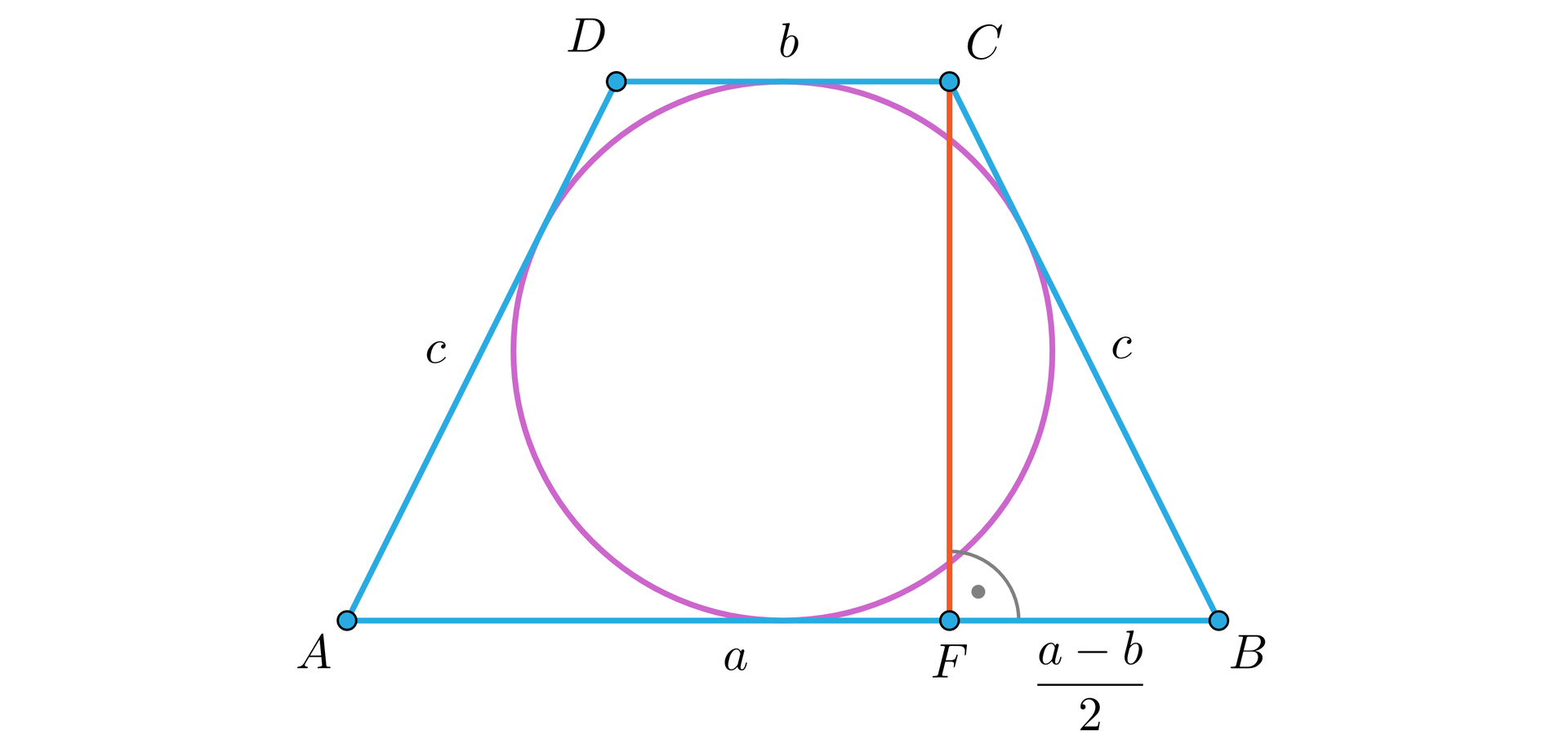
Pole tego trapezutrapeztrapezu jest równe $P=\frac{a+b}{2}·\left|CF\right|$. Ponieważ długość odcinka $FB$, wyznaczonego przez spodek wysokości poprowadzonej z wierzchołka $C$, można opisać jako $\frac{a-b}{2}$, więc $h=\left|CF\right|=\sqrt{c^2-{\left(\frac{a-b}{2}\right)}^2}$. Z twierdzenia o czworokącie opisanym na okręgu wynika, że $2c=a+b$, czyli $c=\frac{a+b}{2}$. Zatem wysokość możemy wyrazić, jako:

$h=\sqrt{{\left(\frac{a+b}{2}\right)}^2-{\left(\frac{a-b}{2}\right)}^2}=\sqrt{\frac{a^2+2ab+b^2-\left(a^2-2ab+b^2\right)}{4}}=\sqrt{\frac{2ab+2ab}{4}}=\sqrt{ab}$.

Wtedy pole trapezu jest równe $P=\frac{a+b}{2}·h=\frac{2c}{2}·\sqrt{ab}=c\sqrt{ab}=\sqrt{c^{2}ab}$, czyli jest równe pierwiastkowi kwadratowemu z iloczynu długości wszystkich boków (z których dwa mają tę samą długość równą $c$).

Przykład 1

Rozważmy trapez równoramienny opisany na okręgu, w którym różnica długości podstaw jest równa $10$, a ramiona mają długość $13$. Wyznaczymy długości podstaw trapezu oraz promień okręgu wpisanego w ten trapeztrapeztrapez.

Rozwiązanie:

RAjEhAqmnlZKY

Ilustracja przedstawia trapez równoramienny ABCD w który wpisano okrąg. Dłuższa podstawa trapezu ma długość a , krótsza długość b a boki mają długość c. Jedna wysokość trapezu została opuszczona z punktu C do punktu F a druga wysokość trapezu została opuszczona z punktu D do punktu E dzielącego podstawę AB na odcinki AE , EF i FB . Odcinki AE i FB mają długość $\frac{a-b}{2}$.

Przyjmijmy oznaczenia, jak na rysunku. Wtedy $a-b=10$ oraz $\frac{a-b}{2}=5$.

Ale z twierdzenia o czworokącie opisanym na okręgu wynika, że $a+b=2·13=26$.

Możemy więc zapisać układ równań $\left\{\begin{array}{l}a-b=10\\ a+b=26\end{array}\right.$.

Korzystając z metody przeciwnych współczynników, mamy, że $2a=36$, czyli $a=18$. Stąd $b=8$.

Oczywiście wysokość trapezu, a w konsekwencji promień okręgu wpisanego, jako połowę tej wysokości, można obliczyć korzystając z twierdzenia Pitagorasa. My jednak skorzystamy z twierdzenia, które udowodniliśmy powyżej oraz z własności, na mocy której pole każdego wielokąta opisanego na okręgu jest równe iloczynowi połowy obwodu przez promień okręgu wpisanego w ten wielokąt.

Ponieważ $P_{ABCD}=\sqrt{13·13·18·8}=156$ oraz $P_{ABCD}=\frac{13+13+18+8}{2}·r=26·r$, więc $r=\frac{156}{26}=6$.

Słownik