Przeczytaj

Objętość prostopadłościanu

Pojęcie objętości jest związane z życiem codziennym. Jeżeli mówimy o objętości, to obliczamy pojemność naczynia, ilość powietrza znajdującego się w pomieszczeniu, czy ilość wody w akwarium.

ObjętośćobjętośćObjętość prostopadłościanu obliczamy ze wzoru:

V = a \cdot b \cdot c

gdzie:
$V$ – objętość,
$a$ , $b$ , $c$ – długości krawędzi (wymiary prostopadłościanu).

R1OK0tNx2acBQ

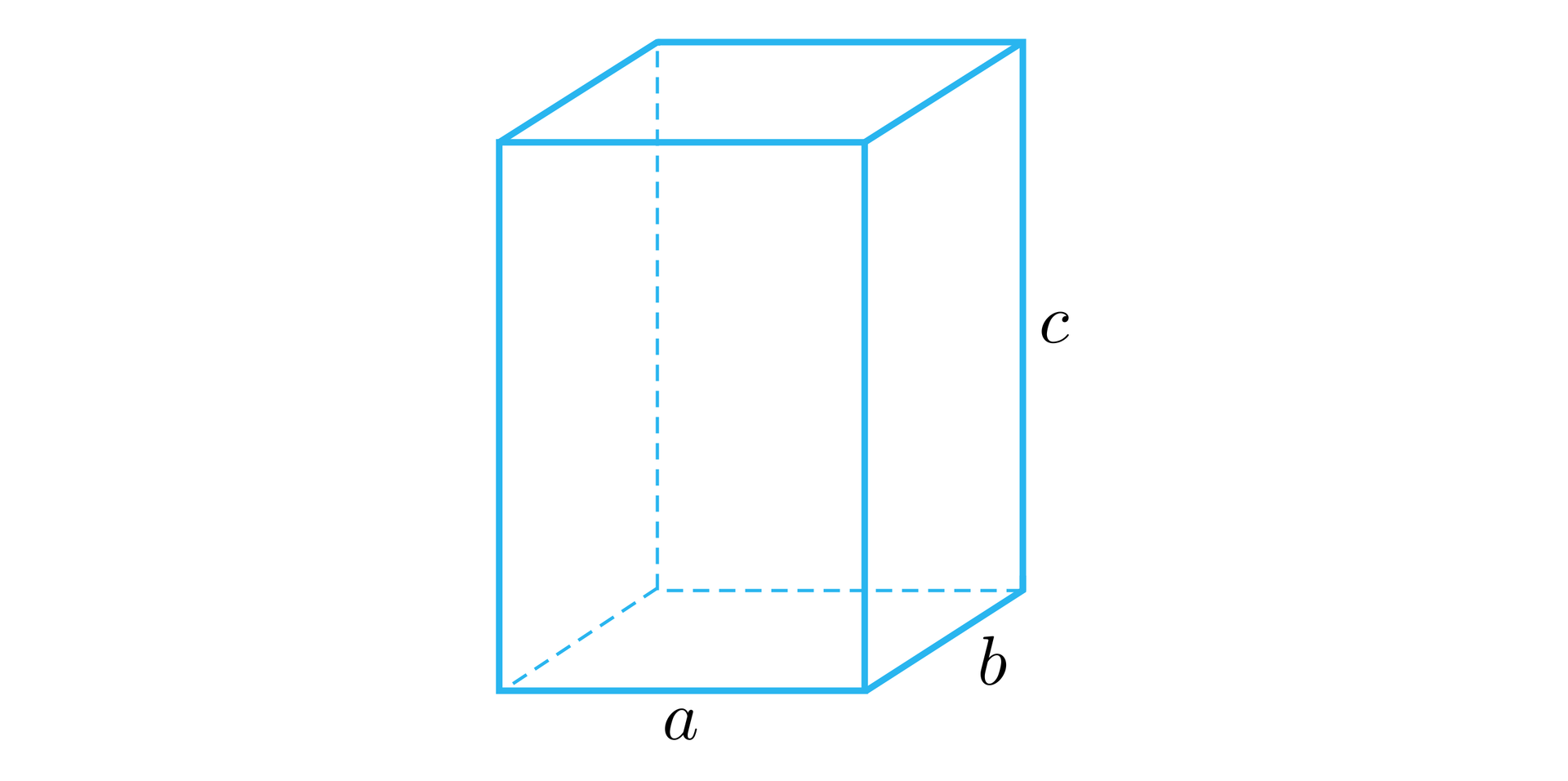
Ilustracja przedstawia prostopadłościan o krawędziach podstawy a i b oraz wysokości c.

Zauważmy, że wielkość $a \cdot b$ jest równa polu podstawy prostopadłościanu, zatem objętość prostopadłościanuprostopadłościanprostopadłościanu możemy obliczyć ze wzoru

V = P_{p} \cdot c

Wobec tego do obliczenia objętości prostopadłościanu wystarczy pomnożyć jego wymiary: długość, szerokość i wysokość. Ważne, aby wszystkie wymiary były podane w jednakowej jednostce.

Przykład 1

Obliczymy objętość prostopadłościanu o krawędziach: $a = 10 cm$ , $b = 15 cm$ i $c = 5 cm$ .

Rozwiązanie:

Objętość podanej bryły wyliczamy według poznanego już wzoru:

$V = a \cdot b \cdot c$

$V = 10 cm \cdot 15 cm \cdot 5 cm$

$V = 750 {cm}^{3}$ .

Objętość prostopadłościanu o wymiarach $10$ , $15$ oraz $5 cm$ wynosi $750$ centymetrów sześciennych.

Objętość podawana jest w jednostkach sześciennych. Dla ułatwienia zapisu czasami jednostkę będziemy pomijać.

Przykład 2

Obliczymy długość trzeciej krawędzi prostopadłościanu, jeżeli objętość prostopadłościanu jest równa $280 m^{3}$ , a dwie z jego krawędzi mają długość $5 m$ oraz $7 m$ .

Rozwiązanie:

Długość trzeciej krawędzi obliczymy, przekształcając wzór na objętość prostopadłościanu:

$V = a \cdot b \cdot c$

$c = \frac{V}{a \cdot b}$

$c = \frac{280 m^{3}}{5 m \cdot 7 m}$

$c = 8 m$ .

Długość trzeciej krawędzi prostopadłościanu wynosi $8$ metrów. Poprzez przekształcenia wzoru na objętość prostopadłościanu możemy obliczyć długość dowolnej krawędzi prostopadłościanu.

Do obliczania objętości prostopadłościanu wykorzystuje się wartości funkcji trygonometrycznych.

Przykład 3

Dany jest prostopadłościan, w którym jedna z krawędzi podstawy ma długość $6$ . Kąty między krawędziami podstawy a przekątnymi ścian bocznych mają miary odpowiednio $α = 30 °$ i $β = 60 °$ , tak jak na poniższym rysunku. Obliczymy objętość tego prostopadłościanu.

R12qB3FyrmtHM

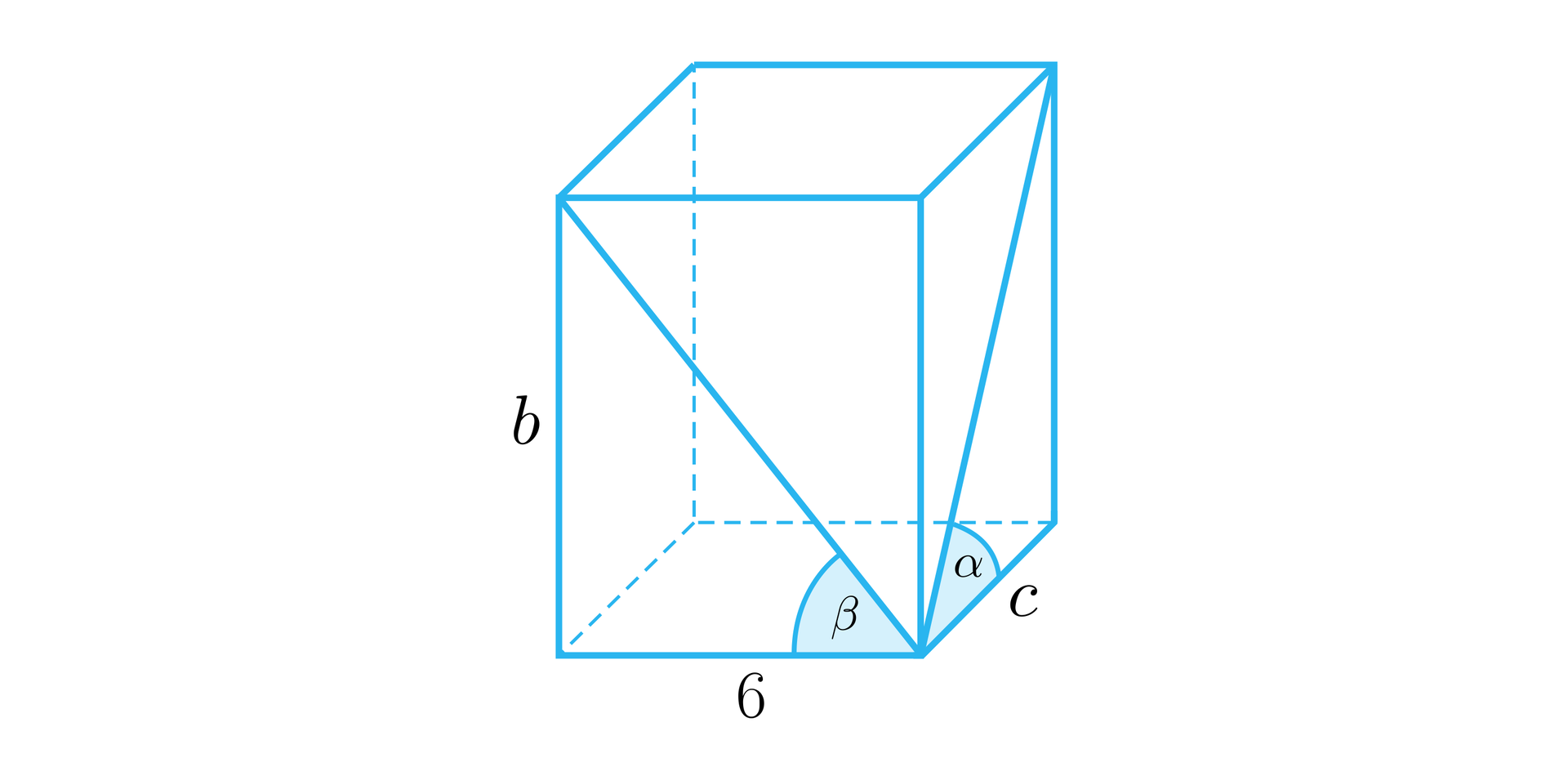
Ilustracja przestawia prostopadłościan, którego krawędzie podstawy mają długości odpowiednio: 6 oraz c, a ściana boczna ma wysokość b. Tylne krawędzie prostopadłościanu narysowano linią przerywaną. Nachylenie przekątnej ściany do krawędzi o długości 6 oznaczono kątem beta, a nachylenie przekątnej ściany bocznej do krawędzi c oznaczono jako alfa.

Rozwiązanie:

Aby rozwiązać zadanie, niezbędna jest umiejętność posługiwania się wzorami trygonometrycznymi oraz własnościami trójkątów. Obliczmy długość krawędzi $b$ . Wykorzystamy do tego wartość funkcji cotangens:

$ctg β = \frac{\sqrt{3}}{3}$

$ctg β = \frac{a}{b}$

$\frac{\sqrt{3}}{3} = \frac{6}{b}$

$b \sqrt{3} = 18$ , czyli $b = 6 \sqrt{3}$

Do obliczenia długość trzeciej krawędzi wykorzystamy funkcję tangens:

$tg α = \frac{\sqrt{3}}{3}$

$tg α = \frac{b}{c}$

$\frac{\sqrt{3}}{3} = \frac{6 \sqrt{3}}{c}$

$c \sqrt{3} = 18 \sqrt{3}$ , czyli $c = 18$

Wobec tego obliczamy objętość prostopadłościanu:

$V = 6 \cdot 6 \sqrt{3} \cdot 18 = 648 \sqrt{3}$

Zauważmy, że do wyznaczenia długości pozostałych krawędzi prostopadłościanu wystarczyła jedynie długość jednej z krawędzi i kąty między krawędziami podstawy i przekątnymi ścian bocznych. Nie zawsze znamy bowiem dokładne długości krawędzi, a zmierzenie odpowiednich kątów może być łatwiejszym zadaniem.

Przykład 4

Przekątna podstawy prostopadłościanu jest o $2$ krótsza od krawędzi bocznej i o $4$ krótsza od przekątnej prostopadłościanu. Wyznaczymy objętość tego prostopadłościanu, jeżeli długości krawędzi podstawy prostopadłościanu różnią się o $3$ .

Rozwiązanie:

Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na rysunku.

R9zQHp9y7TFGy

Ilustracja przedstawia prostopadłościan o krawędziach podstawy a+3 i a oraz wysokości x+2. Przekątna graniastosłupa ma długość x+4, a przekątna podstawy ma długość x.

Ponieważ przekątna podstawy prostopadłościanu, krawędź boczna i przekątna prostopadłościanu tworzą trójkąt prostokatny, zatem do wyznaczenia wartości $x$ rozwiązujemy równanie:

$x^{2} + {(x + 2)}^{2} = {(x + 4)}^{2}$

$x^{2} + x^{2} + 4 x + 4 = x^{2} + 8 x + 16$

$x^{2} - 4 x - 12 = 0$

$x_{1} = \frac{4 - 8}{2} = - 2$ oraz $x_{2} = \frac{4 + 8}{2} = 6$ .

Zatem przekątna podstawy prostopadłościanu ma długość $6$ .

Do wyznaczenia wartości $a$ rozwiązujemy równanie, korzystając z twierdzenia Pitagorasa:

${(a + 3)}^{2} + a^{2} = 6^{2}$

$2 a^{2} + 6 a - 27 = 0$

$a_{1} = \frac{- 6 - 6 \sqrt{7}}{4} < 0$

$a_{2} = \frac{- 6 + 6 \sqrt{7}}{4} = \frac{- 3 + 3 \sqrt{7}}{2} > 0$

Krawędź prostopadłościanu mają długości:

$a = \frac{- 3 + 3 \sqrt{7}}{2}$

$a + 3 = \frac{- 3 + 3 \sqrt{7}}{2} + 3 = \frac{3 + 3 \sqrt{7}}{2}$

$x + 2 = 6 + 2 = 8$

Wobec tego objętość prostopadłościanu jest równa:

$V = \frac{3 + 3 \sqrt{7}}{2} \cdot \frac{- 3 + 3 \sqrt{7}}{2} \cdot 8 = 108$

Przykład 5

Przekątna $d$ prostopadłościanu jest nachylona do największej ściany bocznej pod kątem $α$ . Krawędzie prostopadłościanu wychodzące z tego samego wierzchołka tworzą ciąg arytmetyczny o różnicy $1$ . Wyznaczymy objętość tego prostopadłościanu.

Rozwiązanie:

Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.

RjqLcaMmjJ48K

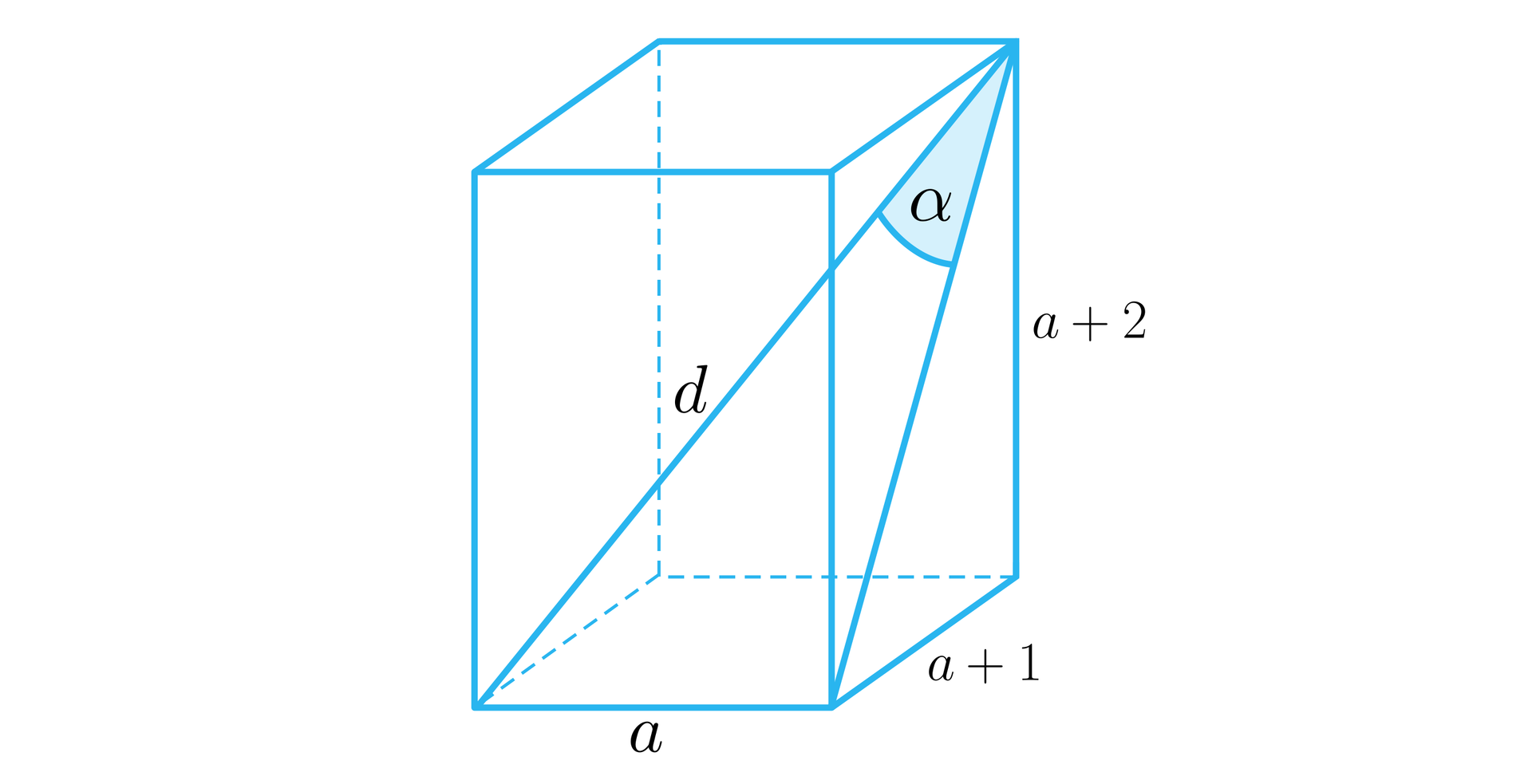
Ilustracja przedstawia prostopadłościan o krawędziach podstawy a i a+1 oraz wysokości a+2. Przekątna graniastosłupa ma długość d, a kąt pomiędzy przekątną graniastosłupa a przekątną ściany bocznej wynosi alfa.

Korzystając z funkcji trygonometrycznej sinus mamy:

$\sin α = \frac{a}{d}$ , więc $a = d \sin α$

Wobec tego

$a + 1 = d \sin α + 1$

$a + 2 = d \sin α + 2$

Objętość prostopadłościanu jest równa:

$V = d \sin α \cdot (d \sin α + 1) \cdot (d \sin α + 2) = d^{3} \sin^{3} α + 3 d^{2} \sin^{2} α + 2 d \sin α$

Przykład 6

Przekątna prostopadłościanu ma długość $26$ i tworzy z płaszczyzną podstawy kąt $α$ taki, że $tg α = \frac{5}{12}$ . Obliczymy objętość tego prostopadłościanu, jeżeli krawędzie podstawy pozostają w stosunku $1 : 3$ .

Rozwiązanie:

Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na poniższym rysunku.

RxlUb3D6p5TY9

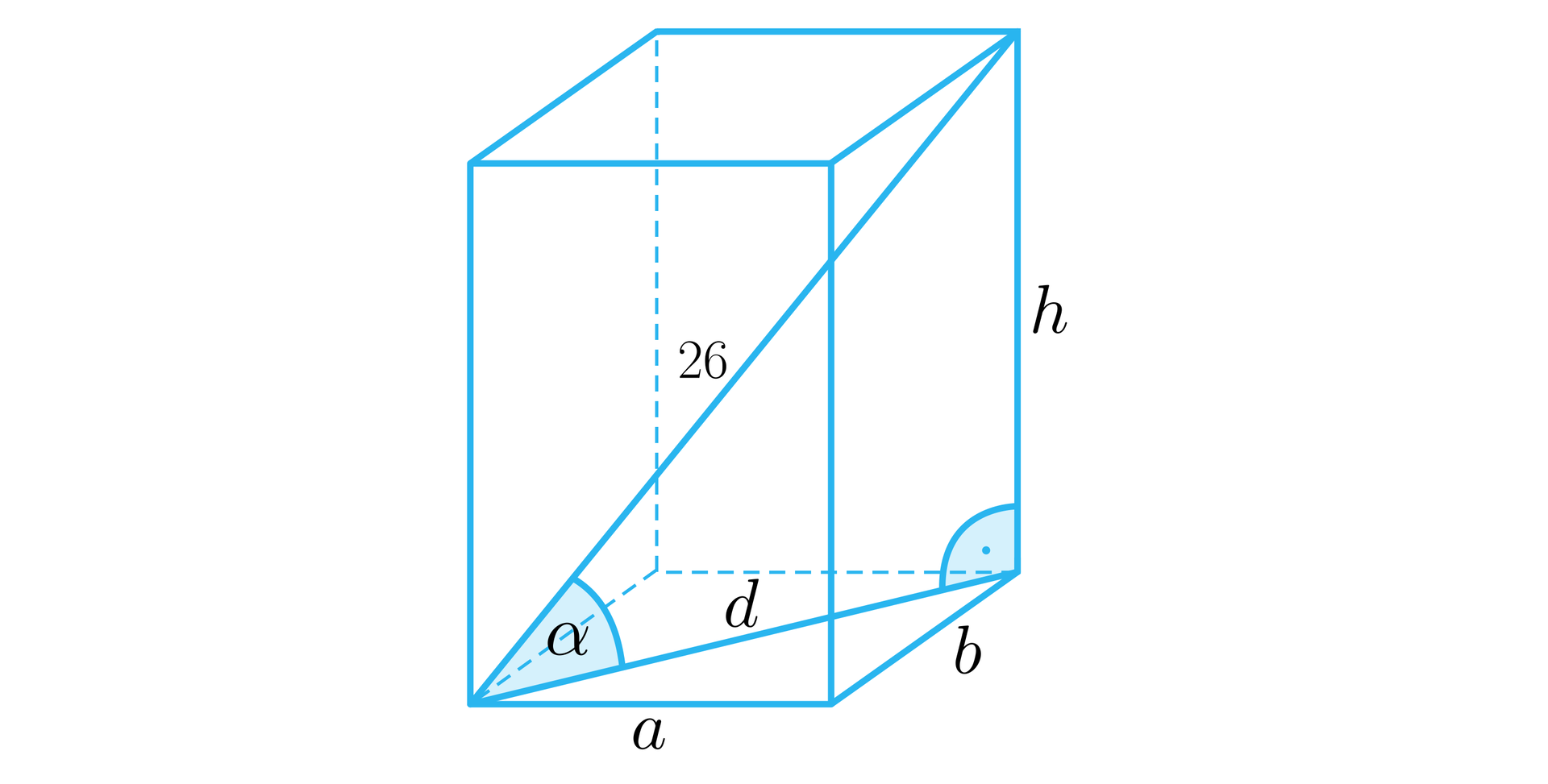
Ilustracja przedstawia prostopadłościan o krawędziach podstawy a i b oraz wysokości h. przekątna podstawy ma długość d, a przekątna graniastosłupa ma długość 26 jednostek. Kąt pomiędzy przekątnymi ma miarę alfa

Ponieważ $tg α = \frac{5}{12}$ , zatem

$\frac{h}{d} = \frac{5}{12}$

$h = \frac{5}{12} \cdot d$ .

Korzystając z twierdzenia Pitagorasa mamy zależność:

$d^{2} + h^{2} = 26^{2}$

$d^{2} + {(\frac{5}{12} \cdot d)}^{2} = 26^{2}$

$d^{2} + \frac{25}{144} d^{2} = 676$

$\frac{169}{144} d^{2} = 676$

$d = 26 \cdot \frac{12}{13} = 24$

$h = \frac{5}{12} \cdot 24 = 10$

Ponieważ krawędzie podstawy pozostają w stosunku $1 : 3$ , zatem załóżmy, że $a = 3 b$ .

Korzystając z twierdzenia Pitagorasa obliczamy długości krawędzi podstawy prostopadłościanu:

$a^{2} + b^{2} = d^{2}$

${(3 b)}^{2} + b^{2} = 24^{2}$

$10 b^{2} = 576$

$b^{2} = \frac{576}{10}$

$b = \frac{24}{\sqrt{10}} = \frac{24 \sqrt{10}}{10} = \frac{12 \sqrt{10}}{5}$

$a = 3 \cdot \frac{12 \sqrt{10}}{5} = \frac{36 \sqrt{10}}{5}$

Wobec tego objętość prostopadłościanu jest równa:

$V = a \cdot b \cdot h$

$V = \frac{36 \sqrt{10}}{5} \cdot \frac{12 \sqrt{10}}{5} \cdot 10 = 1728$

Przykład 7

Wyznaczymy objętość prostopadłościanu z rysunku, gdy dane są długości przekątnych jego ścian bocznych, czyli odcinki $y, z, t$ .

Rozwiązanie:

Narysujmy prostopadłościan i wprowadźmy oznaczenia, jak na rysunku.

R8uxJ8ddqUtAL

Ilustracja przedstawia prostopadłościan o krawędziach podstawy a i b oraz wysokości c. Przekątna podstawy ma długość t, przekątne ściany bocznej mają długości y oraz z. przekątna prostopadłościanu ma długość x.

Wiadomo, że objętość prostopadłościanu obliczamy ze wzoru:

$V = a \cdot b \cdot c$

Prostopadłościan o podanych długościach przekątnych ścian bocznych istnieje, gdy zachodzą następujące warunki:

$y^{2} + t^{2} > z^{2}$

$z^{2} + t^{2} > y^{2}$

$y^{2} + z^{2} > t^{2}$

Korzystając z twierdzenia Pitagorasa otrzymujemy, że:

$a^{2} + b^{2} = t^{2}$

$b^{2} + c^{2} = y^{2}$

$a^{2} + c^{2} = z^{2}$

Korzystając z tych równości otrzymujemy długości krawędzi prostopadłościanu.

Zatem:

$a = \sqrt{\frac{t^{2} + z^{2} - y^{2}}{2}}$

$b = \sqrt{\frac{t^{2} + y^{2} - z^{2}}{2}}$

$c = \sqrt{\frac{y^{2} + z^{2} - t^{2}}{2}}$

Zatem objętość prostopadłościanu z rysunku wyraża się wzorem:

$V = a \cdot b \cdot c = \sqrt{\frac{t^{2} + z^{2} - y^{2}}{2} \cdot \frac{t^{2} + y^{2} - z^{2}}{2} \cdot \frac{y^{2} + z^{2} - t^{2}}{2}} =$

$= \sqrt{\frac{(t^{2} + z^{2} - y^{2}) \cdot (t^{2} + y^{2} - z^{2}) \cdot (y^{2} + z^{2} - t^{2})}{8}}$

Słownik

prostopadłościan

równoległościan, którego dwie dowolne ściany mające wspólną krawędź są prostopadłe

objętość

miara przestrzeni, którą zajmuje bryła w przestrzeni trójwymiarowej

Wprowadzenie

Schemat interaktywny

Objętość prostopadłościanu

Słownik