Przeczytaj

Proporcjonalnością odwrotną nazywamy zależność między wielkościami $x$ i $y$ postaci

y = \frac{a}{x}

gdzie:
$x \neq 0$ i $a \neq 0$ . Liczbę $a$ nazywamy współczynnikiem proporcjonalności odwrotnej.

Wykresem proporcjonalności odwrotnej jest krzywa zwana hiperbolą. Położenie hiperboli w układzie współrzędnych uzależnione jest od znaku współczynnika proporcjonalności $a$ :

R1KaxnYKBtkIB

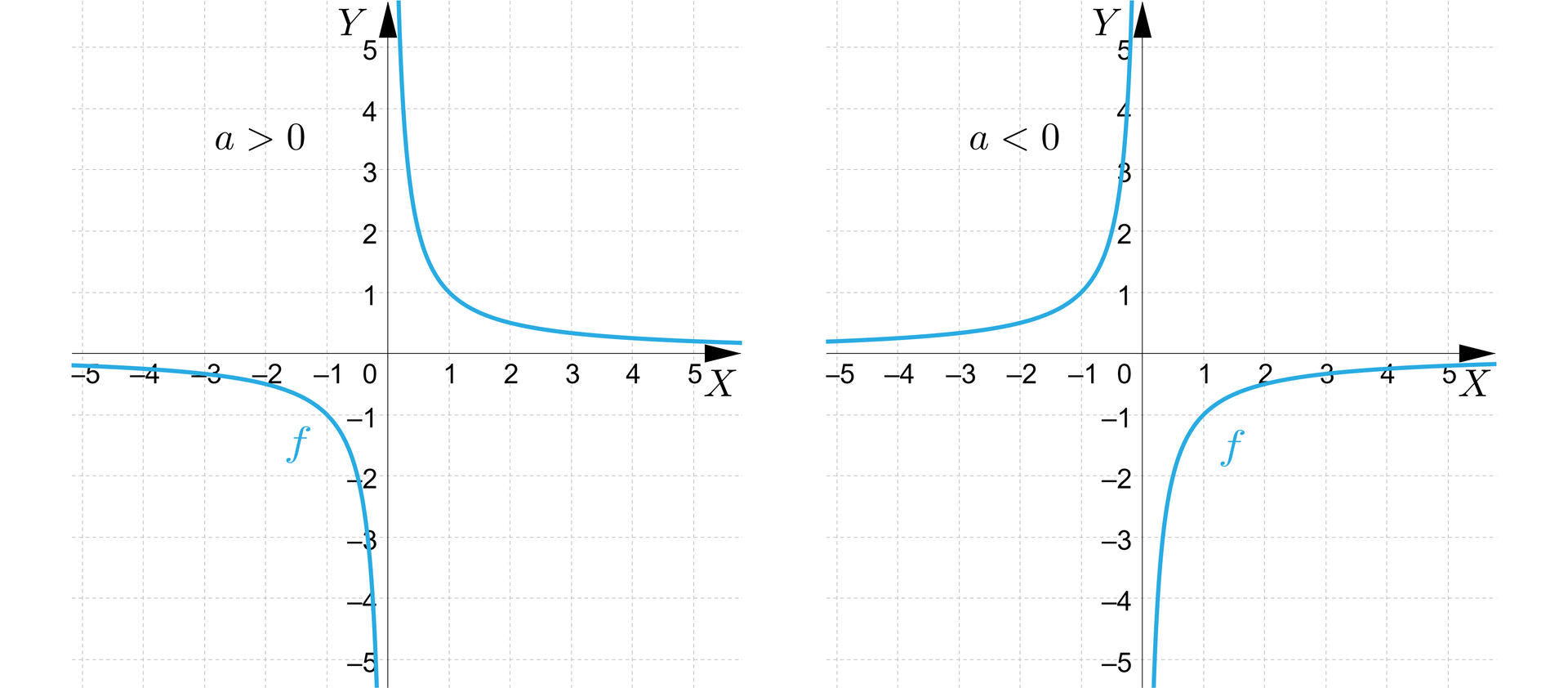
Ilustracja przedstawia dwa wykresy funkcji homograficznych. Ilustracja pierwsza przedstawia poziomą oś X od minus pięciu do pięciu i pionową oś Y od minus pięciu do pięciu. Na rysunku zaznaczono wykres malejącej funkcji homograficznej przechodzącej przez punkty nawias minus jeden średnik minus jeden koniec nawiasu oraz nawias jeden średnik jeden koniec nawiasu. Ilustracja druga przedstawia poziomą oś X od minus pięciu do pięciu i pionową oś Y od minus pięciu do pięciu. Na rysunku zaznaczono wykres rosnącej funkcji homograficznej przechodzącej przez punkty nawias minus jeden średnik jeden koniec nawiasu oraz nawias jeden średnik minus jeden koniec nawiasu.

Jak pokazują wykresy, proporcjonalność odwrotna jest funkcją, która nie posiada miejsc zerowych; jej dziedziną, a także zbiorem wartości, jest zbiór $ℝ ∖ \{0\}$ .

Dla $a > 0$ proporcjonalność odwrotna jest funkcją malejącą, natomiast dla $a < 0$ funkcją rosnącą.

Jeżeli hiperbolę przesuniemy wzdłuż osi $X$ o $p$ jednostek ( $p > 0$ w prawo, $p < 0$ w lewo), otrzymamy funkcję o wzorze:

f (x) = \frac{a}{x - p}

Jeżeli hiperbolę przesuniemy wzdłuż osi $Y$ o $q$ jednostek ( $q > 0$ w górę, $q < 0$ w dół), otrzymamy funkcję o wzorze:

f (x) = \frac{a}{x} + q

Po przesunięciu wykresu funkcji $y = \frac{a}{x}$ wzdłuż osi $X$ lub/i $Y$ otrzymamy funkcję homograficzną, której postać kanoniczna wyraża się wzorem:

f (x) = \frac{a}{x - p} + q

Proste o równaniach $x = p$ oraz $y = q$ są wówczas asymptotamiasymptota krzywejasymptotami wykresu funkcji homograficznej.

Inną postacią funkcji homograficznej jest:

f (x) = \frac{a x + b}{c x + d}

Przykład 1

Rozwiążemy algebraicznie równanie: $\frac{6}{x} - 1 = \frac{2}{x - 1}$ oraz przedstawimy jego ilustrację graficzną.

Rozwiązanie:

$\frac{6}{x} - 1 = \frac{2}{x - 1}$

Określimy dziedzinę równania: $D = ℝ ∖ \{0, 1\}$ .

Pomnożymy obustronnie dane równanie przez iloczyn $x (x - 1)$ .

Otrzymamy wówczas równanie równoważne: $6 (x - 1) - x (x - 1) = 2 x$

$6 x - 6 - x^{2} + x - 2 x = 0$

$- x^{2} + 5 x - 6 = 0$

$∆ = 25 - 4 \cdot 6 = 25 - 24 = 1$

$x_{1} = \frac{- 5 - 1}{- 2} = 3$ oraz $x_{2} = \frac{- 5 + 1}{- 2} = 2$ .

Sprawdzamy, czy uzyskane rozwiązania należą do dziedziny równania, tj. do zbioru $ℝ ∖ \{0, 1\}$ .

Odpowiedź:

Równanie ma dwa rozwiązania: $x_{1} = 3$ oraz $x_{2} = 2$ .

Ilustracja graficzna równania sprowadza się do pokazania punktów wspólnych wykresów funkcji, znajdujących się po obu stronach równania, tj. $f (x) = \frac{6}{x} - 1$ oraz $g (x) = \frac{2}{x - 1}$ .

Sporządzimy zatem wykresy tych funkcji.

RQfXjBgmVeSlw

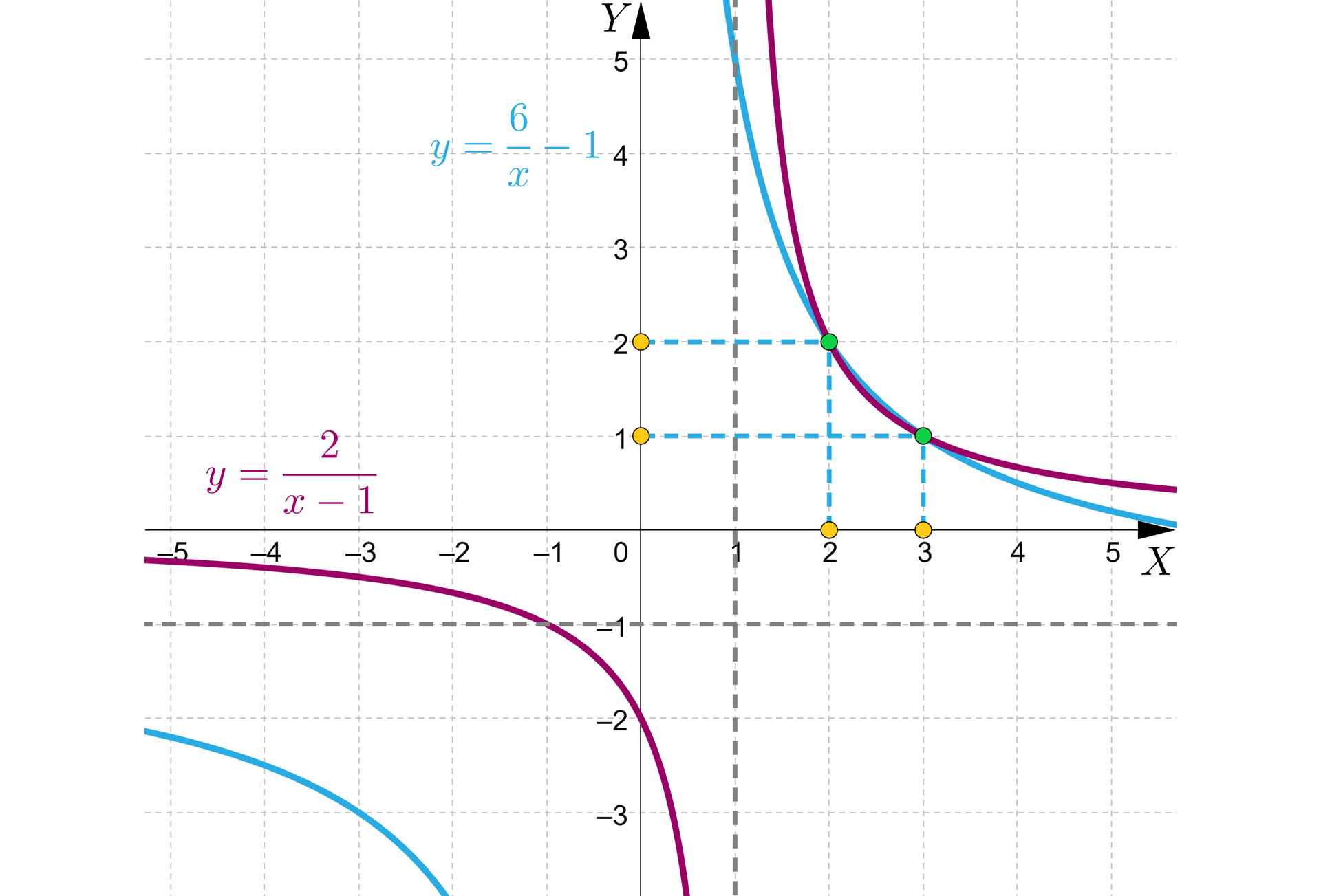
Ilustracja przedstawia poziomą oś X od minus pięciu do pięciu i pionową oś Y od minus pięciu do pięciu. Na rysunku zaznaczono wykresy dwóch malejących funkcji homograficznych. Pierwsza z nich o równaniu y równa się sześć przez x odjąć jeden, ma asymptoty o równaniu x równa się zero i y równa się minus jeden. Wykres przechodzi przez punkty nawias minus trzy średnik minus trzy koniec nawiasu, nawias dwa średnik dwa koniec nawiasu, nawias trzy średnik jeden koniec nawiasu. Druga funkcja o równaniu y równa się dwa przez w mianowniku x odjąć jeden, ma dwie asymptoty pierwsza x równa się jeden oraz druga y równa się zero. Wykres przechodzi przez punkty nawias minus jeden średnik minus jeden koniec nawiasu i przecina wykres pierwszej funkcji w punktach nawias dwa średnik dwa koniec nawiasu, nawias trzy średnik jeden koniec nawiasu.

Wykresy funkcji mają dwa punkty wspólne: odcięteodciętaodcięte tych punktów to rozwiązania równania, a rzędne są równe wartościom obu funkcji dla $x = 2$ oraz $x = 3$ :

$f (2) = g (2) = 2$ ,

$f (3) = g (3) = 1$ .

Zatem wykresy przecinają się w punktach o współrzędnych $(2, 2)$ oraz $(3, 1)$ .

Ważne!

Zwróć uwagę na to, że ilustracja graficzna nie zawsze jest czytelna i nie powinna służyć jako jedyne rozwiązanie zadania, a tylko jako sprawdzenie poprawności obliczeń.

Przykład 2

Wyznaczymy współrzędne punktów $A$ i $B$ przecięcia wykresów funkcji $f (x) = \frac{4}{x + 3}$ oraz $g (x) = x^{2}$ , a następnie wyznaczymy taki punkt $C$ należący do wykresu funkcji f, który wraz z punktami $A$ i $B$ tworzy trójkąt równoramienny o podstawie $A B$ .

Rozwiązanie:

Rozwiążemy równanie: $\frac{4}{x + 3} = x^{2}$ , gdzie $x \neq - 3$ .

Po wykonaniu przekształceń równoważnych otrzymujemy równanie wielomianowe stopnia trzeciego:

$4 = x^{2} (x + 3)$

$x^{3} + 3 x^{2} - 4 = 0$ .

Aby rozwiązać to równanie, posłużymy się twierdzeniem o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych. Nietrudno zauważyć, że jednym z rozwiązań równania jest $x = 1$ . Możemy zatem podzielić wielomian $(x^{3} + 3 x^{2} - 4)$ przez dwumian $(x - 1)$ w celu zapisania go w postaci iloczynowej:

$(x^{3} + 3 x^{2} - 4) : (x - 1) = x^{2} + 4 x + 4$

$x^{3} + 3 x^{2} - 4 = (x^{2} + 4 x + 4) (x - 1)$

Zauważmy także, że trójmian w pierwszym nawiasie jest rozwinięciem kwadratu sumy, więc otrzymujemy następującą postać iloczynową równania:

${(x + 2)}^{2} (x - 1) = 0$ .

Rozwiązaniami równania są zatem liczby: $x_{1} = - 2$ oraz $x_{2} = 1$ .

Są to jednocześnie odcięte punktów przecięcia wykresów funkcji $f$ oraz $g$ .

Ustalimy teraz rzędnerzędnarzędne tych punktów: $f (- 2) = g (- 2) = 4$ oraz $f (1) = g (1) = 1$ .

Szukane punkty mają współrzędne: $A = (- 2, 4)$ oraz $B = (1, 1)$ .

Rozwiążemy graficznie równanie $\frac{4}{x + 3} = x^{2}$ , celem ustalenia położenia punktów $A$ i $B$ .

Wykresem funkcji $f (x) = \frac{4}{x + 3}$ jest hiperbolahiperbolahiperbola, której asymptotą pionową jest prosta $x = - 3$ i która powstaje przez przesunięcie wykresu proporcjonalności odwrotnej $y = \frac{4}{x}$ o $3$ jednostki w lewo. Wykresem zaś funkcji $g (x) = x^{2}$ jest parabola o wierzchołku w początku układu współrzędnych i ramionach skierowanych ku górze. Obie krzywe przechodzą przez punkty $A$ i $B$ .

R13yXtjQD0FXn

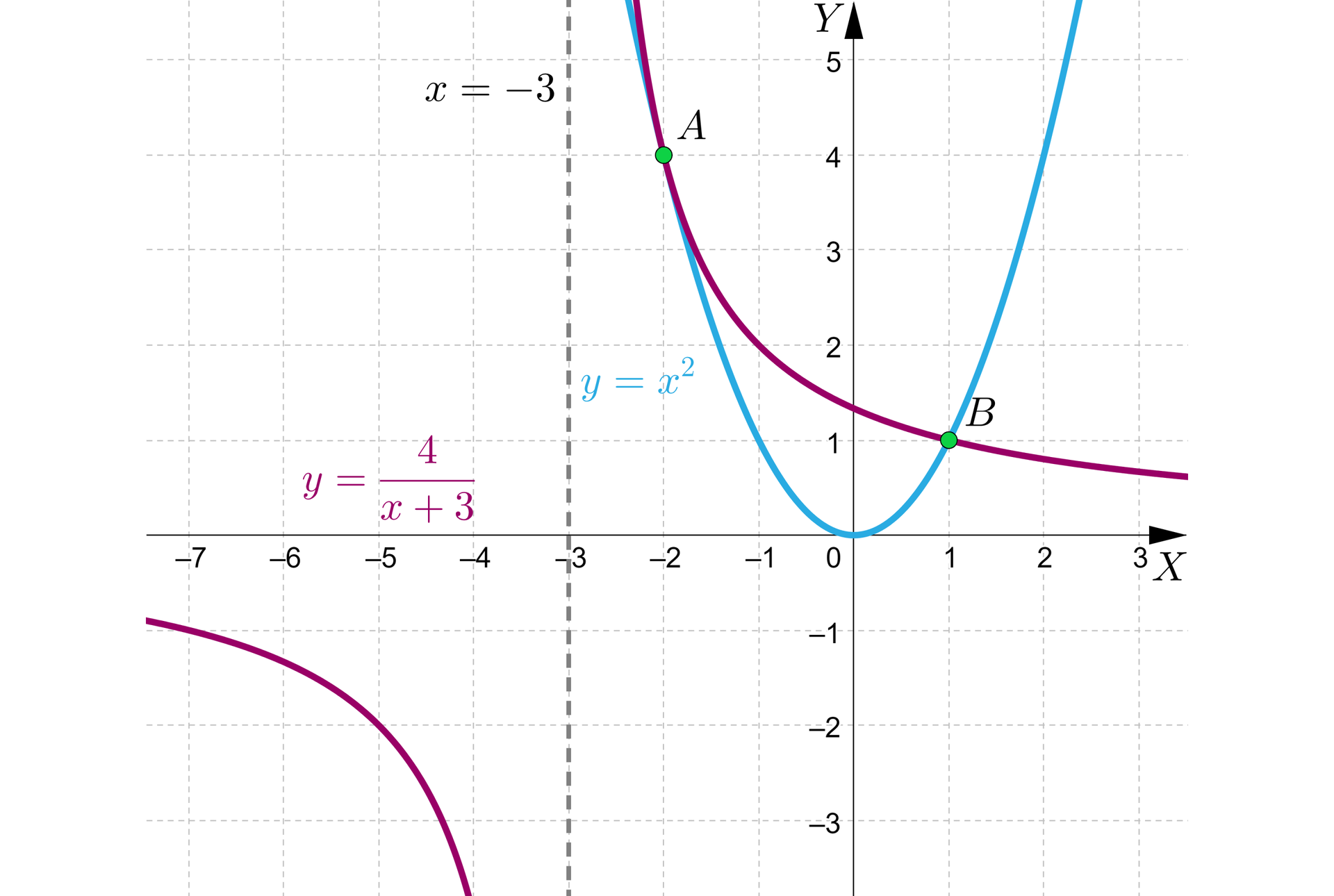
Ilustracja przedstawia poziomą oś X od minus siedmiu do trzech i pionową oś Y od minus trzech do pięciu. Na rysunku zaznaczono wykres funkcji kwadratowej o równaniu y równa się x kwadrat oraz malejącej funkcji homograficznej o równaniu y równa się cztery przez w mianowniku x dodać trzy. Wierzchołek paraboli znajduje się w punkcie nawias zero średnik zero koniec nawiasu a jej ramiona są skierowane w górę. Wykres funkcji homograficznej posiada asymptotę pionową o równaniu x równa się minus trzy i przechodzi przez punkty nawias minus pięć średnik minus dwa koniec nawiasu, nawias minus jeden średnik dwa koniec nawiasu oraz przecina parabolę w punkcie A o współrzędnych nawias minus dwa średnik cztery koniec nawiasu i punkcie B o współrzędnych nawias jeden średnik jeden koniec nawiasu.

Poszukamy punktu $C$ położonego na wykresie funkcji $f$ takiego, że $|A C| = |B C|$ .

Punkt $C$ ma współrzędne $(x, \frac{4}{x + 3})$ . Wyznaczymy długości odcinków $A C$ oraz $B C$ , korzystając ze wzoru na długość odcinka:

$A = (- 2, 4)$ , $B = (1, 1)$ , $C = (x, \frac{4}{x + 3})$

$|A C| = \sqrt{{(x + 2)}^{2} + {(\frac{4}{x + 3} - 4)}^{2}}$

$|B C| = \sqrt{{(x - 1)}^{2} + {(\frac{4}{x + 3} - 1)}^{2}}$

$|A C| = |B C|$

Stąd $\sqrt{{(x + 2)}^{2} + {(\frac{4}{x + 3} - 4)}^{2}} = \sqrt{{(x - 1)}^{2} + {(\frac{4}{x + 3} - 1)}^{2}}$

oraz ${(x + 2)}^{2} + {(\frac{4}{x + 3} - 4)}^{2} = {(x - 1)}^{2} + {(\frac{4}{x + 3} - 1)}^{2}$ .

Po zastosowaniu wzorów skróconego mnożenia, redukcji i uporządkowaniu wyrazów, otrzymujemy:

$18 + 6 x - \frac{24}{x + 3} = 0$ .

Następnie po pomnożeniu obu stron równania przez $(x + 3)$ i ponownym uporządkowaniu dostajemy:

$x^{2} + 6 x + 5 = 0$ .

Równanie to ma dwa rozwiązania: $x_{1} = - 5$ oraz $x_{2} = - 1$ .

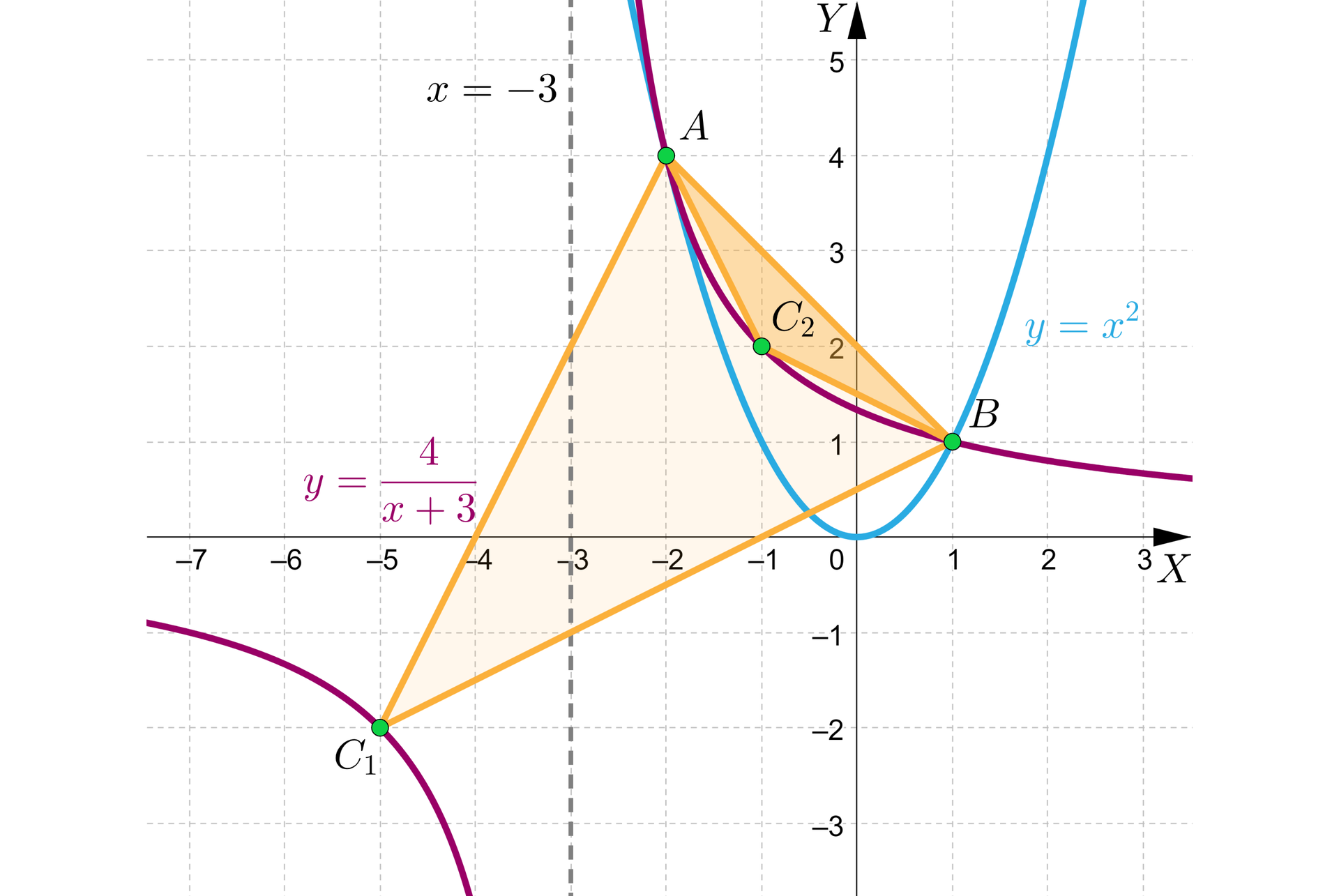
Zatem istnieją dwa takie punkty $C_{1} = (- 5, - 2)$ oraz $C_{2} = (- 1, 2)$ , będące wraz z punktami $A$ i $B$ wierzchołkami trójkąta równoramiennego, co ilustruje poniższa grafika.

R1JPdlwbvuHkI

Przykład 3

Uczniowie klasy $III a$ wynajęli autokar wycieczkowy, płacąc kwotę $3600 zł$ . Tuż przed wycieczką aż sześcioro uczniów tej klasy musiało pozostać w kwarantannie domowej, co podwyższyło koszt wynajęcia autokaru o $20 zł$ dla każdego uczestnika. Obliczymy, ilu uczniów miało pierwotnie uczestniczyć w wycieczce.

Rozwiązanie:

Oznaczmy przez $x$ liczbę uczniów, którzy mieli uczestniczyć w wycieczce, a przez $y$ koszt wynajęcia autokaru przypadający na jednego uczestnika. Zatem $x \cdot y = 3600$ złotych.

Ponieważ jednak ostatecznie w wycieczce uczestniczyło $(x - 6)$ uczniów, a koszt jednostkowy wzrósł do kwoty $(y + 20) zł$ , więc $(x - 6) (y + 20) = 3600$ .

Rozwiążemy zatem układ dwóch równań z dwiema niewiadomymi, przyjmując założenia, że $x > 6$ oraz $y > 0$ .

$\{\begin{cases} x \cdot y = 3600 \\ (x - 6) (y + 20) = 3600 \end{cases}$

$\{\begin{cases} x \cdot y = 3600 \\ x y + 20 x - 6 y - 120 = 3600 \end{cases}$

$\{\begin{cases} x \cdot y = 3600 \\ 3600 + 20 x - 6 y - 120 = 3600 \end{cases}$

$\{\begin{cases} x \cdot y = 3600 \\ 20 x - 6 y - 120 = 0 \end{cases}$

$\{\begin{cases} x \cdot y = 3600 \\ 20 x - 120 = 6 y | : 6 \end{cases}$

$\{\begin{cases} x \cdot y = 3600 \\ y = \frac{10}{3} x - 20 \end{cases}$

$\{\begin{cases} x (\frac{10}{3} x - 20) = 3600 \\ y = \frac{10}{3} x - 20 \end{cases}$

$\{\begin{cases} \frac{10}{3} x^{2} - 20 x = 3600 | : 10 \\ y = \frac{10}{3} x - 20 \end{cases}$

$\{\begin{cases} \frac{1}{3} x^{2} - 2 x = 360 | \cdot 3 \\ y = \frac{10}{3} x - 20 \end{cases}$

$\{\begin{cases} x^{2} - 6 x = 1080 \\ y = \frac{10}{3} x - 20 \end{cases}$

$\{\begin{cases} x^{2} - 6 x - 1080 = 0 \\ y = \frac{10}{3} x - 20 \end{cases}$

$∆ = 36 + 4 \cdot 1080 = 4356$

$\sqrt{∆} = 66$

$x_{1} = - 30$ , $x_{2} = 36$

Pierwsze z rozwiązań nie odpowiada warunkom zadania $(x > 6)$ , zatem rozwiązaniem jest $x = 36$ .

Warto sprawdzić otrzymany rezultat, tzn. ustalić, że wobec uczestnictwa w wycieczce $36$ osób, każdy zapłaciłby za wynajem autokaru $3600 : 36 = 100$ złotych.

W sytuacji rezygnacji $6$ uczestników kwota wynajmu musiałaby obciążyć $30$ osób, które zapłaciłyby po $3600 : 30 = 120$ złotych, a więc koszt jednostkowy wzrósłby o $20 zł$ , co jest zgodne z treścią zadania.

Odpowiedź:

Pierwotnie w wycieczce miało uczestniczyć $36$ uczniów.

Przykład 4

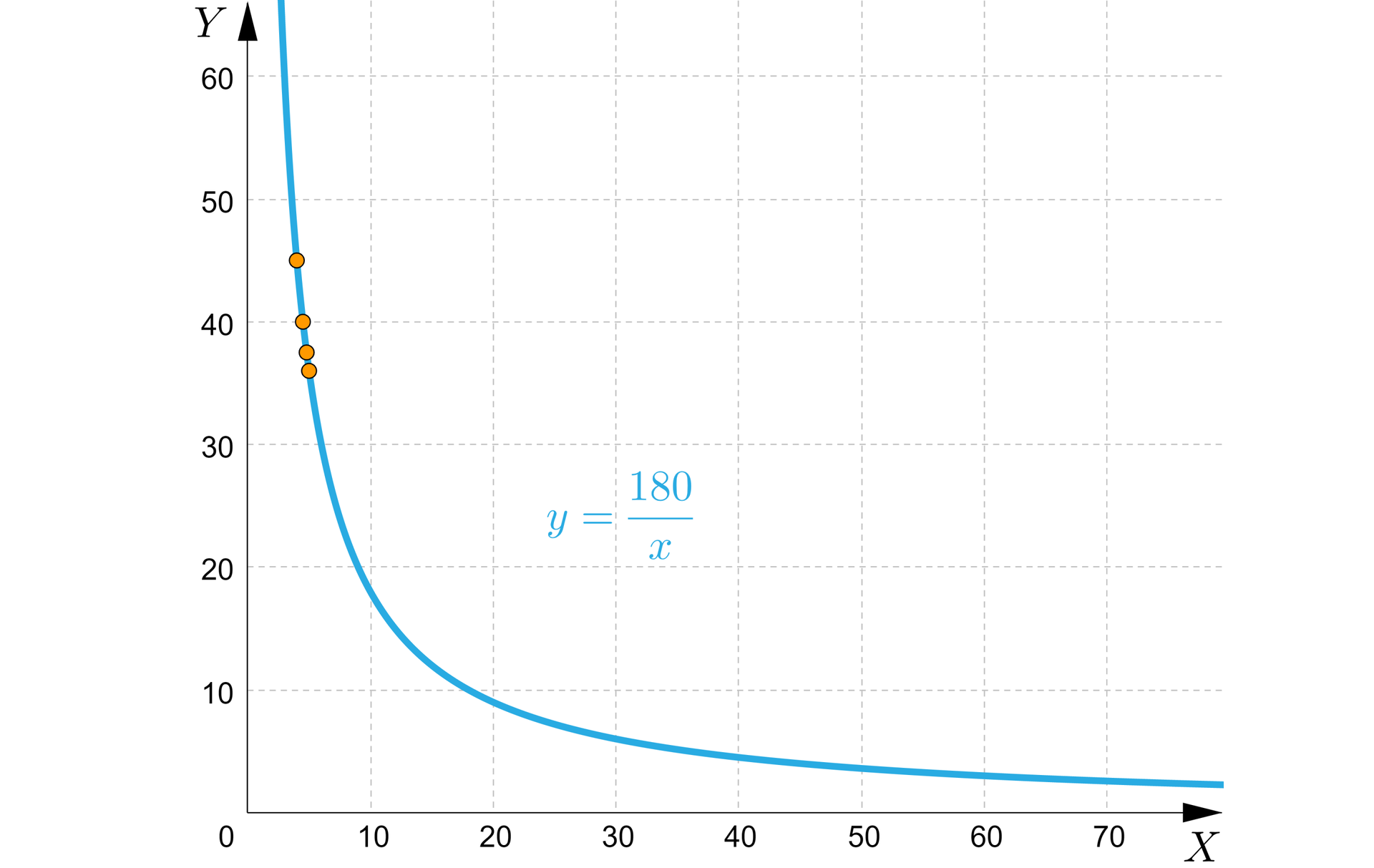
Tata Anki kupuje paliwo zawsze za tę samą kwotę pieniędzy. W lutym cena paliwa wynosiła $4 zł$ za litr i tata Anki zatankował $45$ litrów paliwa, jednak miesiąc później (w marcu) cena wzrosła o $12, 5 %$ , a w kolejnym miesiącu (kwietniu) tata Anki kupił o $2, 5$ litra paliwa mniej niż w marcu. W maju natomiast, po kolejnych podwyżkach cen paliw, zatankował o $1, 5$ litra paliwa mniej niż w poprzednim miesiącu.

a) Zapiszemy wzór funkcji wyrażającej zależność między ceną jednego litra paliwa a ilością zatankowanych litrów, przy stałej kwocie przeznaczonej na ten zakup.

b) Obliczymy cenę paliwa w marcu, kwietniu i maju oraz liczbę litrów paliwa, które zatankował tata Anki w tych miesiącach.

c) Sporządzimy wykres tej zależności.

Rozwiązanie:

a) Oznaczmy przez $x$ cenę $1$ litra paliwa, a przez $y$ liczbę litrów, którą można kupić za ustaloną kwotę pieniędzy.

Obliczymy teraz, jaką kwotę pieniędzy przeznacza każdorazowo tata Anki na zakup paliwa:

$4 \cdot 45 = 180$ .

Zatem wzór szukanej zależności to

$y = \frac{180}{x}$ , gdzie $x > 0$ .

b) Obliczymy cenę paliwa w marcu:

$4 zł \cdot 1, 125 = 4, 50 zł$

oraz liczbę litrów paliwa, które zakupił tata Anki za stałą kwotę $180 zł$ :

$180 : 4, 50 = 40$ .

Dalsze obliczenia przedstawimy w tabeli:

	luty	marzec	kwiecień	maj
Cena paliwa $[zł]$	$4$	$4, 50$	$180 : 37, 5 = 4, 80$	$180 : 36 = 5$
Ilość $[l]$	$45$	$40$	$37, 5$	$36$

RldaRA25XNxBU

Ilustracja przedstawia poziomą oś X od zera do siedemdziesięciu i pionową oś Y od zera do sześćdziesięciu. Na rysunku zaznaczono także wykres malejącej funkcji homograficznej o równaniu y równa się sto osiemdziesiąt przez x. Wykres funkcji przechodzi przez punkty nawias cztery przecinek pół średnik czterdzieści koniec nawiasu oraz nawias pięć średnik trzydzieści sześć koniec nawiasu.

Słownik

hiperbola

krzywa będąca zbiorem takich punktów, dla których wartość bezwzględna różnicy odległości tych punktów od dwóch ustalonych punktów, nazywanych ogniskami hiperboli, jest stała

asymptota krzywej

prosta jest asymptotą danej krzywej, jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej, odległość tego punktu od prostej dąży do zera; asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji

odcięta

pierwsza współrzędna punktu w kartezjańskim układzie współrzędnych (zwanym też prostokątnym układem współrzędnych), również inna nazwa osi $X$

rzędna

druga współrzędna punktu w kartezjańskim układzie współrzędnych (zwanym też prostokątnym układem współrzędnych), oznaczana jest przeważnie symbolem $y$ , równiez inna nazwa osi $Y$

Wprowadzenie

Prezentacja multimedialna

Słownik