Przeczytaj

Przypomnijmy najpierw twierdzenie Pitagorasa, dokładnie wskazując jego założenia i tezę.

Pitagorasa

Twierdzenie: Pitagorasa

Jeżeli trójkąt jest prostokątny, to suma kwadratów długości jego przyprostokątnych jest równa kwadratowi długości jego przeciwprostokątnej.

Przy oznaczeniach jak na rysunku

R1K75WiowMLd1

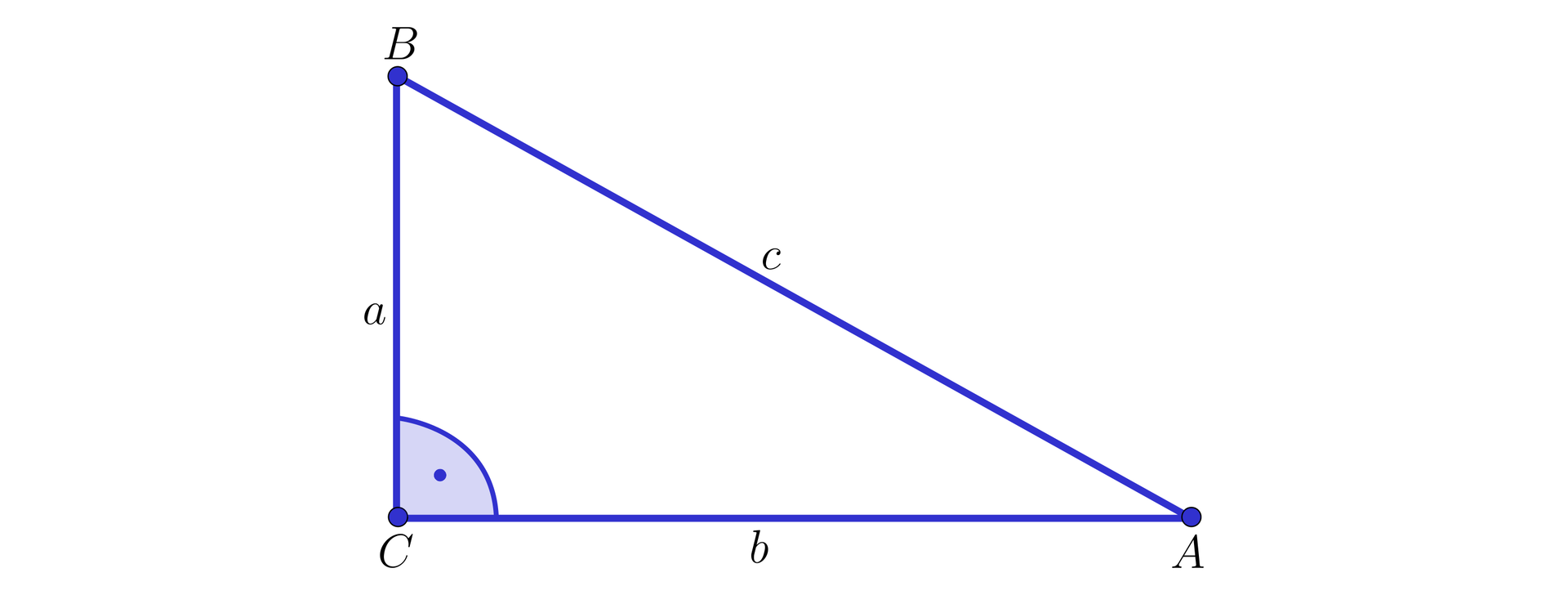
Ilustracja przedstawia trójkąt prostokątny A B C. Trójkąt leży na poziomej przyprostokątnej A C o długość b. Jego druga przyprostokątna B C ma długość a, natomiast jego przeciwprostokątna A B ma długość c.

tezę twierdzenia możemy zapisać w postaci:

a^{2} + b^{2} = c^{2}

Zwróć uwagę, że twierdzenie Pitagorasa stosujemy wtedy, gdy wiemy, ze trójkąt jest prostokątny. Jest to założenie tego twierdzenia. Równość $a^{2} + b^{2} = c^{2}$ , jaka wtedy zachodzi, to teza twierdzenia. Nie możemy zatem stosować tego twierdzenia w sytuacji, gdy znamy długości boków trójkąta, a chcemy rozstrzygnąć, czy ten trójkąt jest prostokątny. Okazuje się, że prawdziwa jest też implikacja odwrotna, a więc mamy twierdzenie odwrotne do twierdzenia Pitagorasa.

odwrotne do twierdzenia Pitagorasa

Twierdzenie: odwrotne do twierdzenia Pitagorasa

Jeżeli suma kwadratów długości którychś dwóch boków trójkąta jest równa kwadratowi długości trzeciego boku tego trójkąta, to ten trójkąt jest prostokątny.

Jeśli więc oznaczymy długości boków trójkąta przez $a$ , $b$ i $c$ , przy czym $a \leq b \leq c$ , to twierdzenie to możemy sformułować następująco:

Jeżeli $a^{2} + b^{2} = c^{2}$ , to trójkąt jest prostokątny.

Twierdzenie to dostarcza nam kryterium, pozwalające rozstrzygać, czy trójkąt jest prostokątny, czy też nie jest.

Przykład 1

Rozstrzygniemy, czy trójkąt o bokach długości $145$ , $143$ i $24$ jest prostokątny.

Rozwiązanie

Wystarczy sprawdzić, czy $24^{2} + 143^{2}$ jest równe $145^{2}$ . Obliczmy zatem $24^{2} + 143^{2} = 576 + 20449 = 21025$ oraz $145^{2} = 21025$ , zatem $24^{2} + 143^{2} = 145^{2}$ . Z twierdzenie odwrotnego do twierdzenia Pitagorasa wnioskujemy więc, że ten trójkąt jest prostokątny.

Przykład 2

Rozstrzygniemy, czy trójkąt o bokach długości $147$ , $145$ i $24$ jest prostokątny, ostrokątny czy rozwartokątny.

Rozwiązanie

Podobnie jak w poprzednim przykładzie sprawdzamy, czy $24^{2} + 145^{2}$ jest równe $147^{2}$ . To, że równość $24^{2} + 145^{2} = 147^{2}$ nie jest prawdziwa możemy stwierdzić bez obliczania wartości lewej i prawej strony. Wystarczy na przykład zauważyć, że cyfrą jedności liczby $24^{2}$ jest $6$ , cyfrą jedności liczby $145^{2}$ jest $5$ , więc cyfrą jedności liczby $24^{2} + 145^{2}$ jest $1$ . Natomiast cyfrą jedności liczby $147^{2}$ jest $9$ . Wobec tego trójkąt nie jest prostokątny.

Z przyprowadzonego rozumowania nie możemy jednak wywnioskować, czy jest on ostrokątnytrójkąt ostrokątnyostrokątny, czy rozwartokątny. Rozstrzygniemy to, wykorzystując twierdzenie cosinusów. Oznaczmy przez $α$ kąt tego trójkąta leżący naprzeciw najdłuższego boku tego trójkąta, a więc boku o długości $147$ i zastosujmy twierdzenie cosinusów dla tego kąta. Otrzymujemy równość

$147^{2} = 24^{2} + 145^{2} - 2 \cdot 24 \cdot 145 \cdot \cos α$

Stąd obliczmy

$\cos α = \frac{24^{2} + 145^{2} - 147^{2}}{2 \cdot 24 \cdot 145} = \frac{576 + 21025 - 21609}{6960} = \frac{- 8}{6960} = - \frac{1}{870}$

Wartość cosinusa, jaką otrzymaliśmy jest ujemna, a to oznacza, że $α$ jest kątem rozwartym.

Stąd wnioskujemy, że trójkąt jest rozwartokątnytrójkąt rozwartokątnyrozwartokątny.

Analizując Przykład 2 bez trudu zauważysz, że w gruncie rzeczy nie interesowała nas dokładna wartość $\cos α$ , ale tylko to, czy jest to liczba ujemna, czy dodatnia.

Jeśli więc $a$ , $b$ , $c$ oznaczają długości boków trójkąta, natomiast $α$ , $β$ , $γ$ – kąty tego trójkąta leżące – odpowiednio – naprzeciw boków tych długościach, to z twierdzenia cosinusów otrzymujemy:

a^{2} = b^{2} + c^{2} - 2 b c \cos α

b^{2} = a^{2} + c^{2} - 2 a c \cos β

c^{2} = a^{2} + b^{2} - 2 a b \cos γ

Stąd:

\cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c}

\cos β = \frac{a^{2} + c^{2} - b^{2}}{2 a c}

\cos γ = \frac{a^{2} + b^{2} - c^{2}}{2 a b}

Każdy z mianowników ułamków stojących po prawych stronach tych równości jest dodatni, więc o znaku każdego z ułamków decyduje znak licznika tego ułamka.

Zatem, jeśli wszystkie liczby

$b^{2} + c^{2} - a^{2}$ , $a^{2} + c^{2} - b^{2}$ , $a^{2} + b^{2} - c^{2}$ są dodatnie, co jest równoważne temu, że prawdziwe są wszystkie trzy nierówności

$b^{2} + c^{2} > a^{2}$ , $a^{2} + c^{2} > b^{2}$ , $a^{2} + b^{2} > c^{2}$ , to cosinusy wszystkich trzech kątów trójkąta są dodatnie, co oznacza, że wszystkie trzy kąty trójkąta są ostre, a to oznacza, że trójkąt jest ostrokątny.

Jeśli jedna z liczb

$b^{2} + c^{2} - a^{2}$ , $a^{2} + c^{2} - b^{2}$ , $a^{2} + b^{2} - c^{2}$ jest równa zero, co jest równoważne temu, że prawdziwa jest jedna z równości

$b^{2} + c^{2} = a^{2}$ , $a^{2} + c^{2} = b^{2}$ , $a^{2} + b^{2} = c^{2}$ , to oznacza, że jeden z cosinusów kąta trójkąta jest równy zero, a więc jeden z kątów trójkąta jest prosty, a to oznacza, że trójkąt jest prostokątnytrójkąt prostokątnyprostokątny.

Nawiasem mówiąc, mamy wtedy do czynienia z sytuacją, o której mówi twierdzenie odwrotne do twierdzenia Pitagorasa.

Jeśli natomiast jedna z liczb

$b^{2} + c^{2} - a^{2}$ , $a^{2} + c^{2} - b^{2}$ , $a^{2} + b^{2} - c^{2}$ jest ujemna, co jest równoważne temu, że prawdziwa jest jedna z nierówności

$b^{2} + c^{2} < a^{2}$ , $a^{2} + c^{2} < b^{2}$ , $a^{2} + b^{2} < c^{2}$ , to oznacza, że jeden z cosinusów kąta trójkąta jest ujemny, a więc jeden z kątów trójkąta jest rozwarty, a to oznacza, że trójkąt jest rozwartokątny.

Udowodniliśmy w ten sposób następujące twierdzenie rozstrzygające, kiedy trójkąt o danych bokach jest ostrokątnytrójkąt ostrokątnyostrokątny, kiedy jest prostokątny, a kiedy jest rozwartokątny. Możemy powiedzieć, że jest to uogólnienie twierdzenia Pitagorasa i twierdzenia do niego odwrotnego.

uogólnione twierdzenia Pitagorasa i twierdzenia do niego odwrotnego

Twierdzenie: uogólnione twierdzenia Pitagorasa i twierdzenia do niego odwrotnego

Jeżeli $a$ , $b$ , $c$ oznaczają długości boków trójkąta, to trójkąt ten jest:

ostrokątny wtedy i tylko wtedy, gdy $b^{2} + c^{2} > a^{2}$ i $a^{2} + c^{2} > b^{2}$ i $a^{2} + b^{2} > c^{2}$ ,

prostokątny wtedy i tylko wtedy, gdy $b^{2} + c^{2} = a^{2}$ lub $a^{2} + c^{2} = b^{2}$ lub $a^{2} + b^{2} = c^{2}$ ,

rozwartokątny wtedy i tylko wtedy, gdy $b^{2} + c^{2} < a^{2}$ lub $a^{2} + c^{2} < b^{2}$ lub $a^{2} + b^{2} < c^{2}$ .

Jeśli jesteśmy w stanie ustalić, który z boków trójkąta jest najdłuższy (wtedy kąt leżący naprzeciw tego boku jest największy), to wystarczy sprawdzić jak ma się suma kwadratów długości dwóch krótszych boków do kwadratu długości najdłuższego. To znaczy:

Jeżeli $a$ , $b$ , $c$ oznaczają długości boków trójkąta oraz $a \leq b \leq c$ , to trójkąt ten jest:

ostrokątny wtedy i tylko wtedy, gdy $a^{2} + b^{2} > c^{2}$ ,

prostokątnytrójkąt prostokątnyprostokątny wtedy i tylko wtedy, gdy $a^{2} + b^{2} = c^{2}$ ,

rozwartokątny wtedy i tylko wtedy, gdy $a^{2} + b^{2} < c^{2}$ .

Słownik

trójkąt ostrokątny

trójkąt, którego wszystkie kąty wewnętrzne są ostre

trójkąt prostokątny

trójkąt, którego jeden z kątów wewnętrznych jest prosty (dwa pozostałe są ostre)

trójkąt rozwartokątny

trójkąt, którego jeden z kątów wewnętrznych jest rozwarty (dwa pozostałe są ostre)

Wprowadzenie

Symulacja interaktywna

Słownik