Niech $\mathrm{\Omega }$ będzie skończonym zbiorem wszystkich możliwych zdarzeń elementarnych jednakowo prawdopodobnych.

Prawdopodobieństwem zajścia zdarzenia $A\subset \mathrm{\Omega }$ nazywamy liczbę

Rzucamy dziesięć razy monetą. Obliczymy prawdopodobieństwoklasyczna definicja prawdopodobieństwaprawdopodobieństwo tego, że co najmniej raz wypadła reszka.

W jednokrotnym rzucie monetą mamy dwa zdarzenia elementarne: orzeł, reszka. Zatem w dziesięciokrotnym rzucie monetą mamy $2^{10}$ zdarzeń elementarnych.

$\left|\mathrm{\Omega }\right|=2^{10}$

Oznaczmy:

$A$ – zdarzenie polegające na wyrzuceniu co najmniej jednej reszki (możemy też powiedzieć – przynajmniej jednej reszki lub nie mniej niż jednej reszki) w dziesięciokrotnym rzucie monetą. Wypisywanie i zliczanie zdarzeń sprzyjających zdarzeniu $A$ zajęłoby zbyt wiele czasu. Łatwo też wtedy o pomyłkę.

Rozpatrzymy więc zdarzenie przeciwne – ani razu nie wypadła reszka, czyli za każdym razem wypadł orzeł.

$\left|A\text{'}\right|=1$

Obliczamy prawdopodobieństwo zdarzenia przeciwnego.

$P\left(A\text{'}\right)=\frac{1}{2^{10}}$

Zatem

$P\left(A\right)=1-\frac{1}{2^{10}}=\frac{1024-1}{1024}=\frac{1023}{1024}$

Odpowiedź:

Prawdopodobieństwo tego, że w dziesięciokrotnym rzucie monetą co najmniej raz wypadła reszka jest równe $\frac{1023}{1024}$.

Prawdopodobieństwo, że Marek wygra konkurs matematyczny jest równe $\frac{3}{5}$, a prawdopodobieństwo, że nie wygra konkursu geograficznego jest równe $\frac{5}{8}$. Prawdopodobieństwo, że Marek wygra co najmniej jeden konkurs jest równe $\frac{5}{7}$. Obliczymy prawdopodobieństwo, że Marek wygra oba konkursy.

Oznaczmy:

$M$ – zdarzenie polegające na tym, że Marek wygra konkurs matematyczny,

$G$ – zdarzenie polegające na tym, że Marek wygra konkurs geograficzny.

Wtedy:

$P\left(M\right)=\frac{3}{5}$

$P\left(G\right)=1-\frac{5}{8}=\frac{3}{8}$

$P\left(M\cup G\right)=\frac{5}{7}$

Korzystamy ze wzoru na prawdopodobieństwo sumy.

$P\left(M\cup G\right)=P\left(M\right)+P\left(G\right)-P\left(M\cap G\right)$

Mamy obliczyć $P\left(M\cap G\right)$.

Wstawiamy do wzoru odpowiednie liczby i przekształcamy otrzymane wyrażenie.

$\frac{5}{7}=\frac{3}{5}+\frac{3}{8}-P\left(M\cap G\right)$

$P\left(M\cap G\right)=\frac{24+15}{40}-\frac{5}{7}$

$P\left(M\cap G\right)=\frac{39·7-200}{280}$

$P\left(M\cap G\right)=\frac{39·7-200}{280}=\frac{73}{280}$

Odpowiedź:

Prawdopodobieństwo tego że Marek wygra oba konkursy jest równe $\frac{73}{280}$.

W bombonierce znajdują się dwie czekoladki kawowe i trzy miodowe. Wyjmujemy z bombonierki w sposób losowy najpierw jedną, a następnie drugą czekoladkę. Obliczymy prawdopodobieństwo tego, że dokładnie jedna z czekoladek będzie kawowa.

Oznaczmy:

$K$ – wyjęta czekoladka jest kawowa,

$M$ – wyjęta czekoladka jest miodowa,

$A$ – zdarzenie polegające na wyjęciu dokładnie jednej czekoladki kawowej.

Przebieg rozpatrywanego doświadczenia zilustrujemy za pomocą drzewa.

R1boMiSV0ZN7c

Drzewko przedstawia możliwości losowań. W pierwszym poziomie mamy pudełko z pięcioma czekoladkami: dwiema kawowymi i trzema miodowymi. W drugim poziomie mamy pierwszy etap losowania: 0,4 to prawdopodobieństwo wylosowania kawowej czekoladki, a 0,6 miodowej. Trzeci poziom ilustruje drugi etap losowania. Pierwsza możliwość: po wylosowaniu kawowej czekoladki wylosowano kawową czekoladkę, prawdopodobieństwo tego zdarzenia wynosi 0,25; druga możliwość: po wylosowaniu kawowej czekoladki wylosowano miodową czekoladkę, prawdopodobieństwo tego zdarzenia wynosi 0,75; trzecia możliwość: po wylosowaniu miodowej czekoladki wylosowano kawową czekoladkę, prawdopodobieństwo tego zdarzenia wynosi 0,5; czwarta możliwość: po wylosowaniu miodowej czekoladki wylosowano miodową czekoladkę, prawdopodobieństwo tego zdarzenia wynosi 0,5;

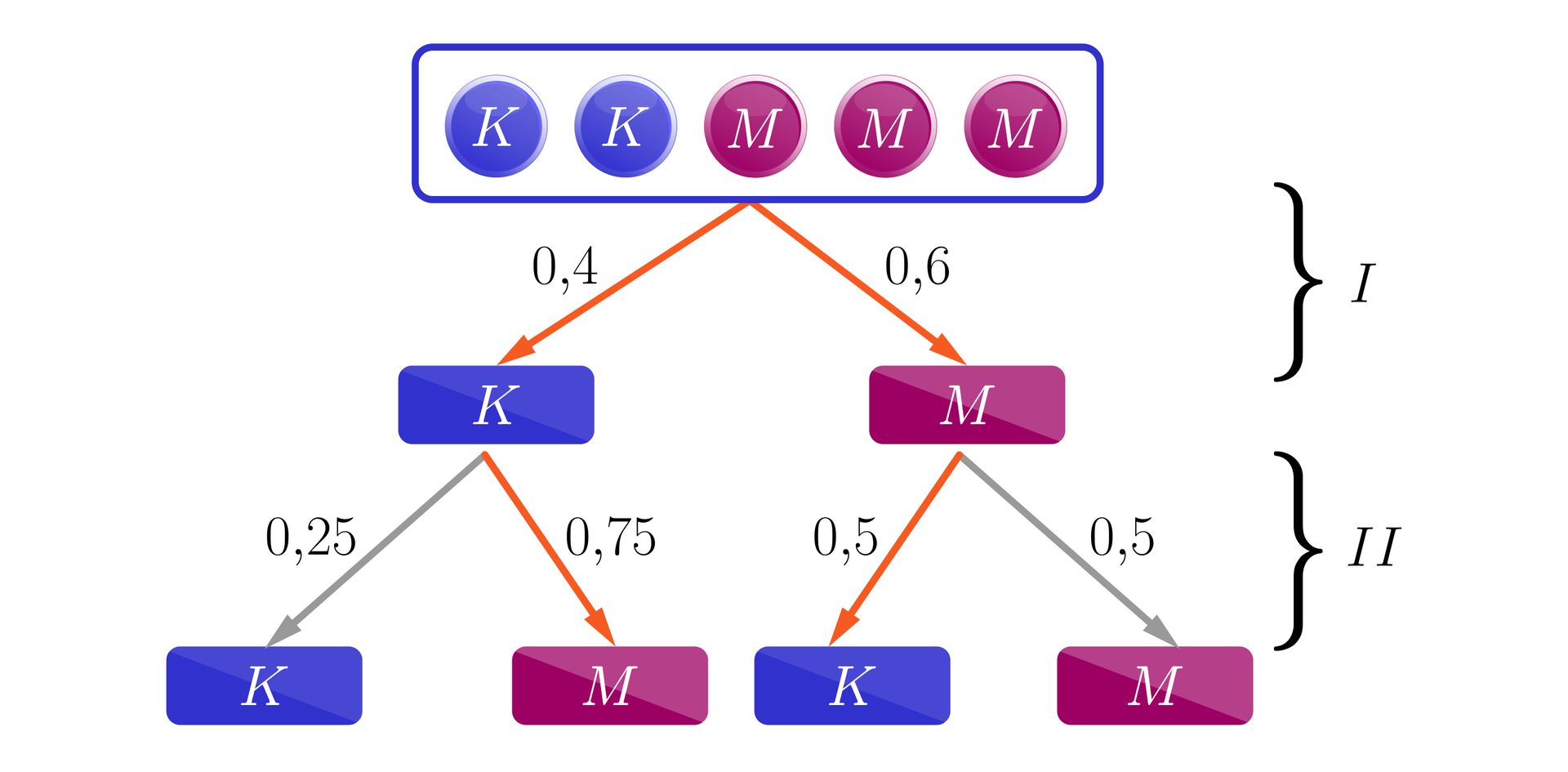
Prawdopodobieństwa zdarzenia $A$ obliczamy, mnożąc prawdopodobieństwa zapisane przy zaznaczonych na czerwono krawędziach i dodając otrzymane liczby.

$P\left(A\right)=0,4·0,75+0,6·0,5=0,3+0,3=0,6$

Odpowiedź:

Prawdopodobieństwo wyjęcia  dokładnie jednej czekoladki kawowej jest równe $0,6$.

Rzucamy dwiema kostkami do gry. Obliczymy prawdopodobieństwo zdarzenia: suma liczb oczek, jakie wypadły na obu kostkach jest co najwyżej równa $5$.

Zaczynamy od wyznaczenia liczby zdarzeń elementarnych w tym doświadczeniu.

$\left|\mathrm{\Omega }\right|=6^2=36$

Jeśli suma liczb oczek na obu kostkach ma być co najwyżej równa $5$ (możemy też powiedzieć – nie większa od $5$) to może być równa $2$, $3$, $4$ lub $5$.

$A=\left\{\left(1,1\right),\left(1,2\right),\left(1,3\right),\left(1,4\right),\left(2,1\right),\left(2,2\right),\left(2,3\right),\left(3,1\right),\left(3,2\right),\left(4,1\right)\right\}$

Zatem

$\left|A\right|=10$

Korzystamy ze wzoru na prawdopodobieństwo klasyczne.

$P\left(A\right)=\frac{10}{36}=\frac{5}{18}$

Odpowiedź:

Prawdopodobieństwo, że w rzucie dwiema kostkami suma liczb wyrzuconych oczek będzie co najwyżej równa $5$, jest równe $\frac{5}{18}$.

Rakieta zaopatrzona jest w pięć silników. Prawdopodobieństwo zepsucia się każdego z nich jest równe $\frac{1}{3}$. Silniki psują się niezależnie od siebie. Obliczymy prawdopodobieństwo tego, że zepsuje się co najwyżej jeden silnik.

Zadanie rozwiążemy, korzystając ze schematu Bernoulliego:

$P\left(S_n=k\right)=\left(\begin{array}{c}n\\ k\end{array}\right)·p^k·q^{n-k}$,

gdzie $p=\frac{1}{3}$, $q=1-\frac{1}{3}=\frac{2}{3}$, $n=5$.

Chcemy obliczyć prawdopodobieństwo tego, że zepsuje się co najwyżej jeden silnik. Mamy dwie możliwości – nie zepsuje się żaden silnik, bądź zepsuje się jeden silnik.

Prawdopodobieństwo tego, że nie zepsuje się żaden silnik jest równe:

$P\left(S_5=0\right)=\left(\begin{array}{c}5\\ 0\end{array}\right)·{\left(\frac{1}{3}\right)}^0·{\left(\frac{2}{3}\right)}^5=1·1·\frac{32}{243}=\frac{32}{243}$

Prawdopodobieństwo tego, że zepsuje się jeden silnik jest równe:

$P\left(S_5=1\right)=\left(\begin{array}{c}5\\ 1\end{array}\right)·{\left(\frac{1}{3}\right)}^1·{\left(\frac{2}{3}\right)}^4=5·\frac{1}{3}·\frac{16}{81}=\frac{80}{243}$

Prawdopodobieństwo tego, że zepsuje się co najwyżej jeden silnik jest równe:

$P\left(S_5⩽1\right)=P\left(S_5=0\right)+P\left(S_5=1\right)=\frac{32}{243}+\frac{80}{243}=\frac{112}{243}$

Odpowiedź:

Szukane prawdopodobieństwo jest równe $\frac{112}{243}$.

niech $\mathrm{\Omega }$ będzie skończonym zbiorem wszystkich możliwych zdarzeń elementarnych jednakowo prawdopodobnych; prawdopodobieństwem zajścia zdarzenia $A\subset \mathrm{\Omega }$ nazywamy liczbę