Przeczytaj
Środkową trójkąta nazywamy odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
Oczywiście w każdym trójkącie są trzy środkowe, zaznaczone na rysunku kolorami.
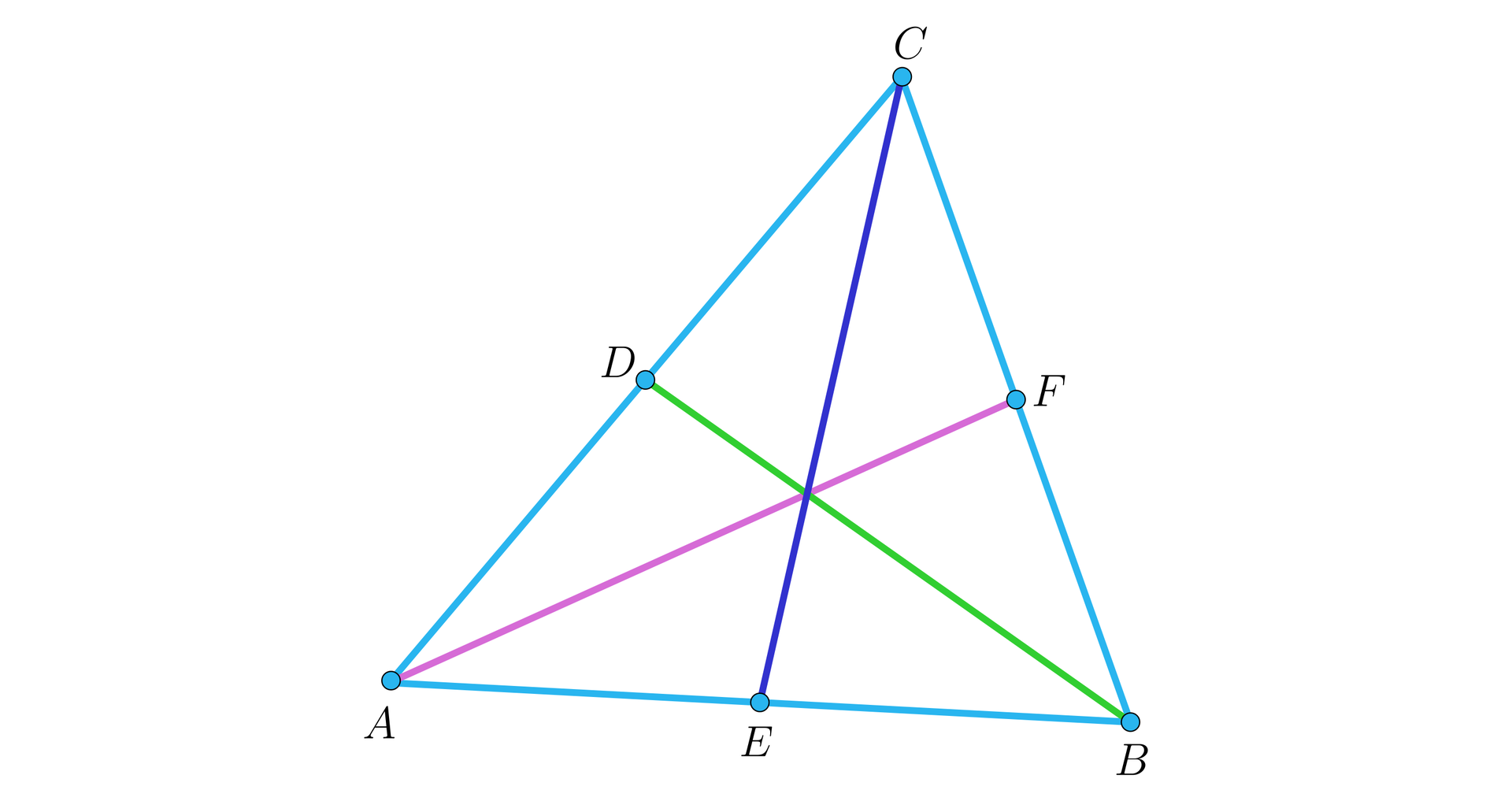
Dowolna środkowa trójkątaśrodkowa trójkąta dzieli ten trójkąt na dwa trójkąty o równych polach.
Weźmy dowolną środkową trójkąta , na przykład . Wtedy trójkąty i mają wspólną wysokość i podstawy równej długości, więc mają równe pola.
Na rysunku na przedłużeniu boku zaznaczono punkt taki, że .
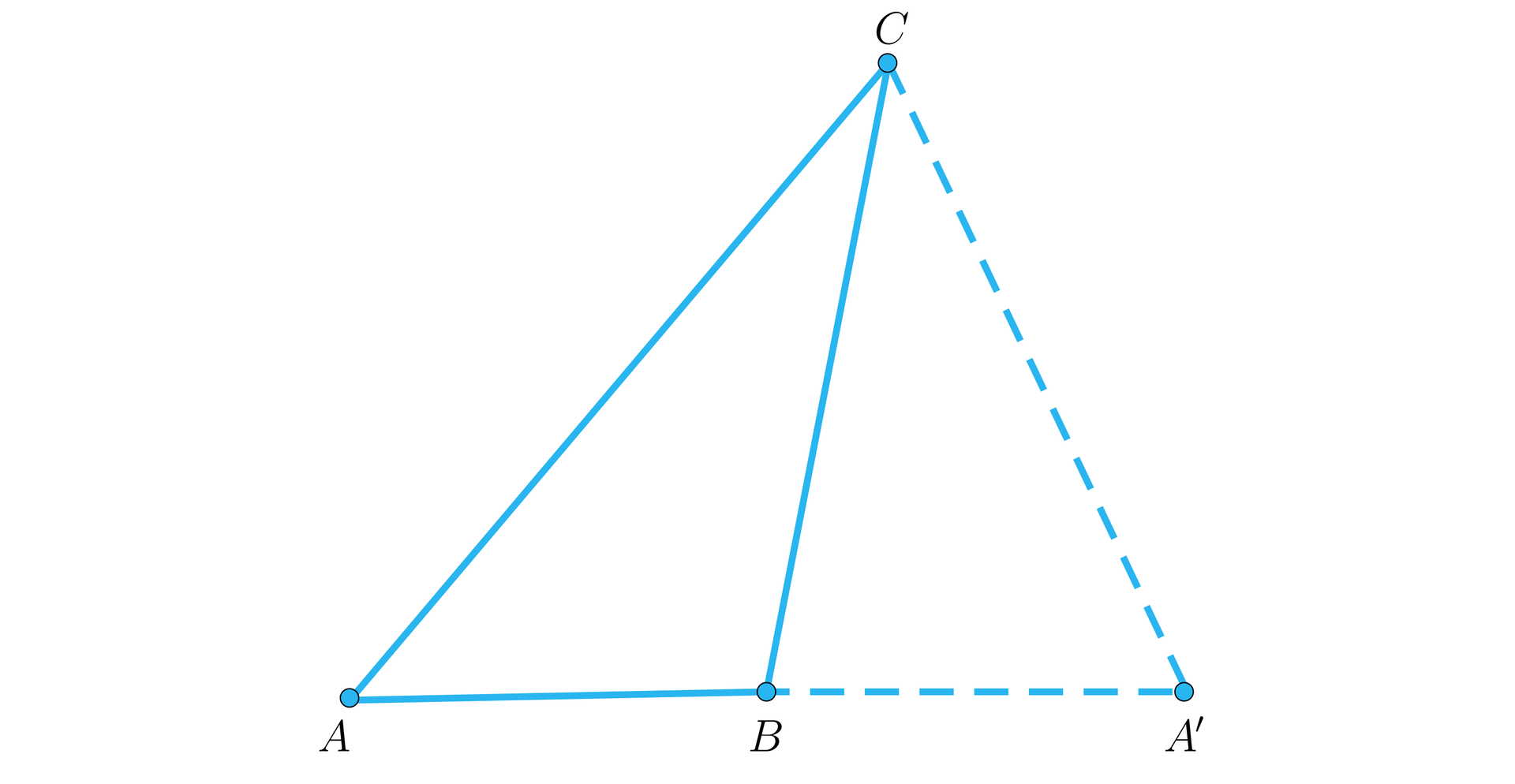
Pokażemy, że pole trójkąta jest dwa razy większe od pola trójkąta .
Rozwiązanie
Rzeczywiście, z równości wynika jest środkową trójkąta , więc . Stąd .
Pokażemy, że jeśli punkt leży na środkowej trójkąta to pola trójkątów i są równe.
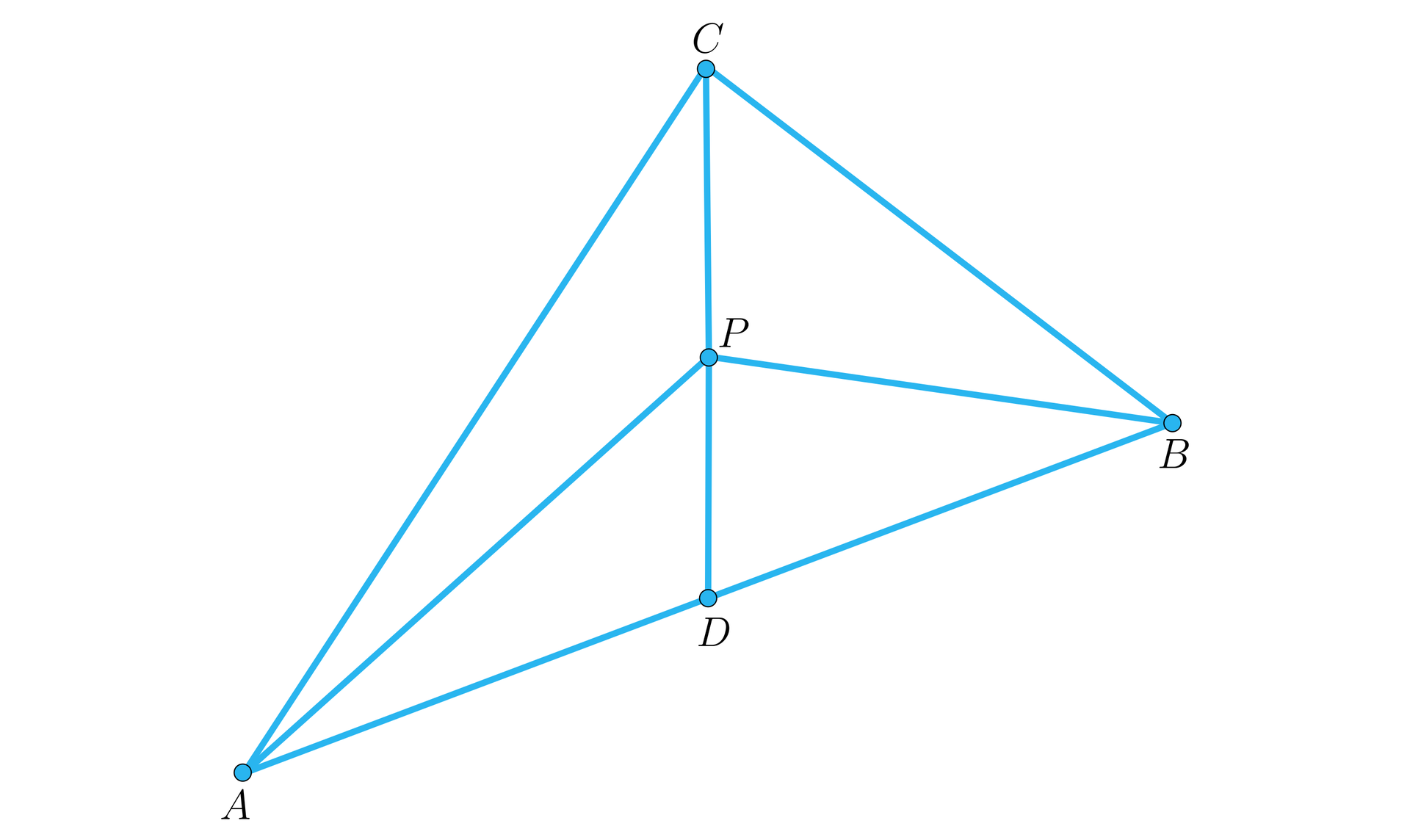
Rozwiązanie
Ponieważ odcinek jest środkową trójkąta , a punkt leży na tej środkowej, to punkt jest środkiem boku trójkąta . Stąd odcinek jest środkową trójkąta . Stąd dzieli on ten trójkąta na dwa trójkąty i o równych polach.
Zanim przejdziemy do głównego twierdzenia w tym materiale, przypomnimy własności linii środkowej w trójkącie, czyli odcinka, który łączy środki dwóch boków w trójkącie.
Linia środkowa w trójkącie jest równoległa do podstawy i długość linii środkowej jest równa połowie długości podstawy.
Twierdzenie główne
Środkowe w trójkącie przecinają się w jednym punkcie i punkt ten dzieli środkowe w stosunku licząc od wierzchołków trójkąta.
Niech będzie punktem przecięcia środkowych , i
w trójkącie .
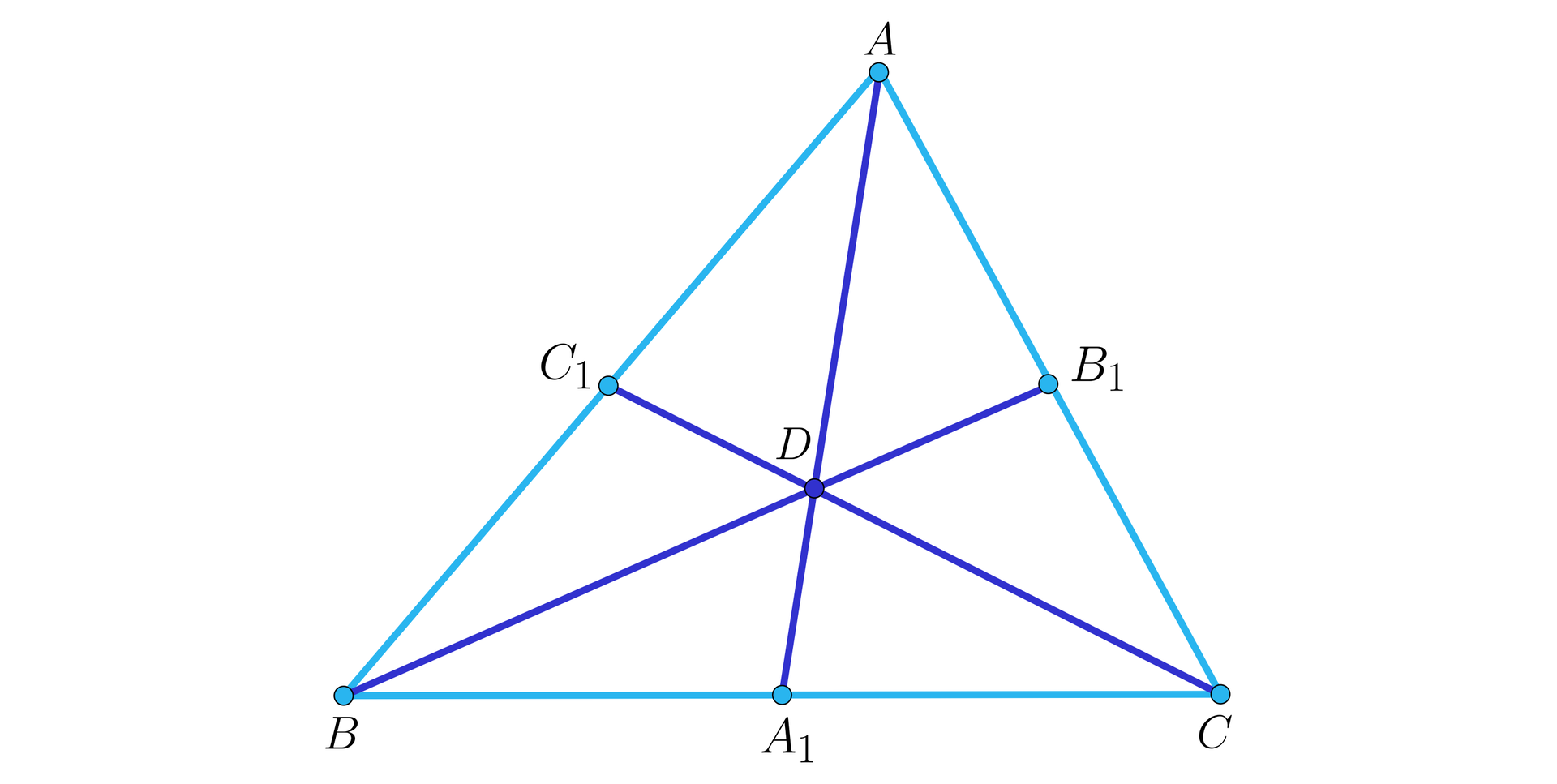
Wyznaczamy na boku punkt taki, że .
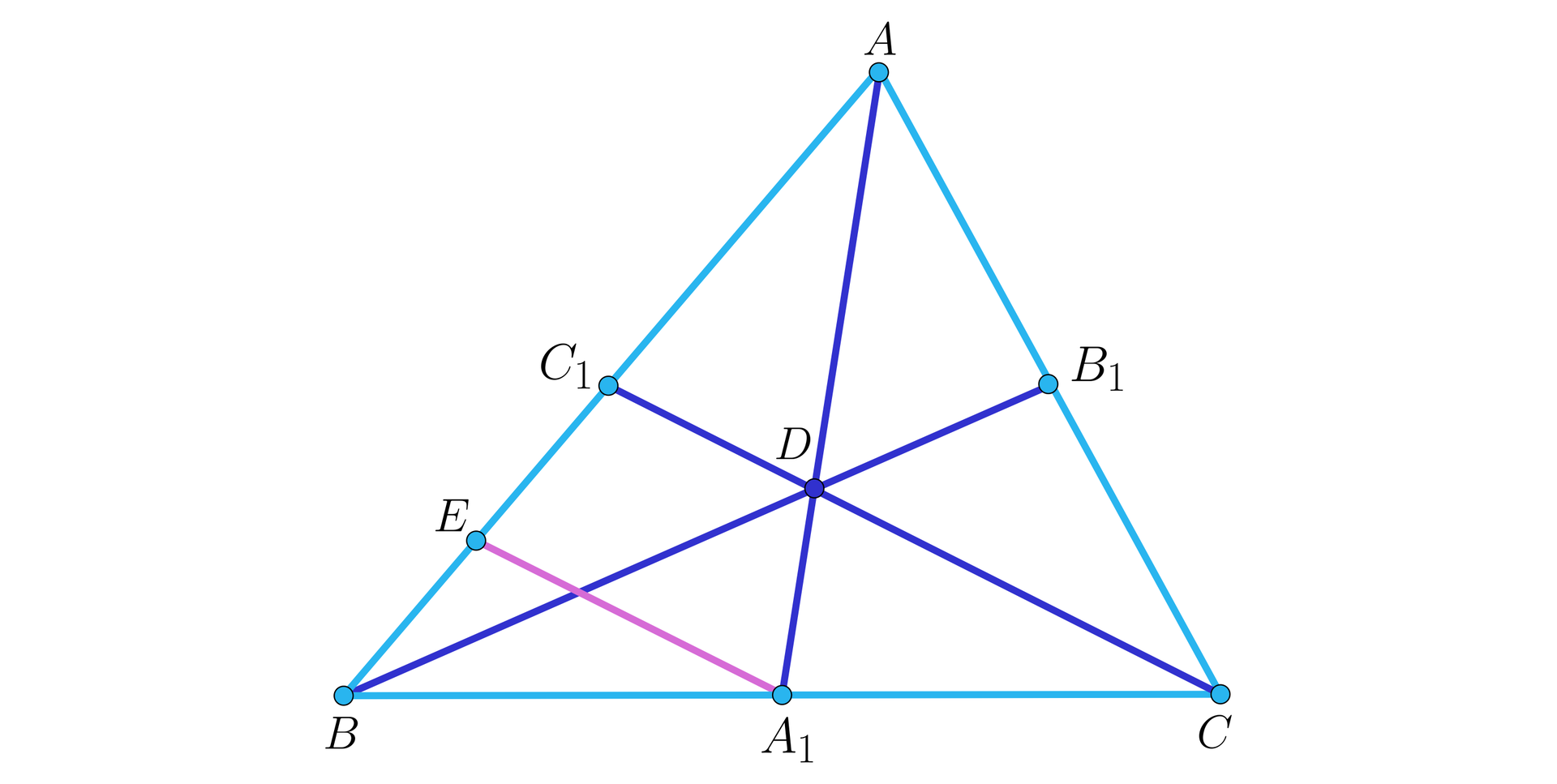
Z twierdzenia Talesa wynika, że , co oznacza, że . Stąd: .
Stostując twierdzenie Talesa do trójkąta i wykorzystując powyższą równość otrzymujemy:
.
Zatem: .
Wnioskujemy stąd, że punkt przecięcia środkowych dzieli każdą środkową w stosunku (od strony wierzchołka). To należało udowodnić.
W trójkącie środkowe i przecinają się w punkcie . Pokażemy, że trójkąt jest podobny do trójkąta w skali , a stąd stosunek pól tych trójkątów wynosi .
Rozwiązanie
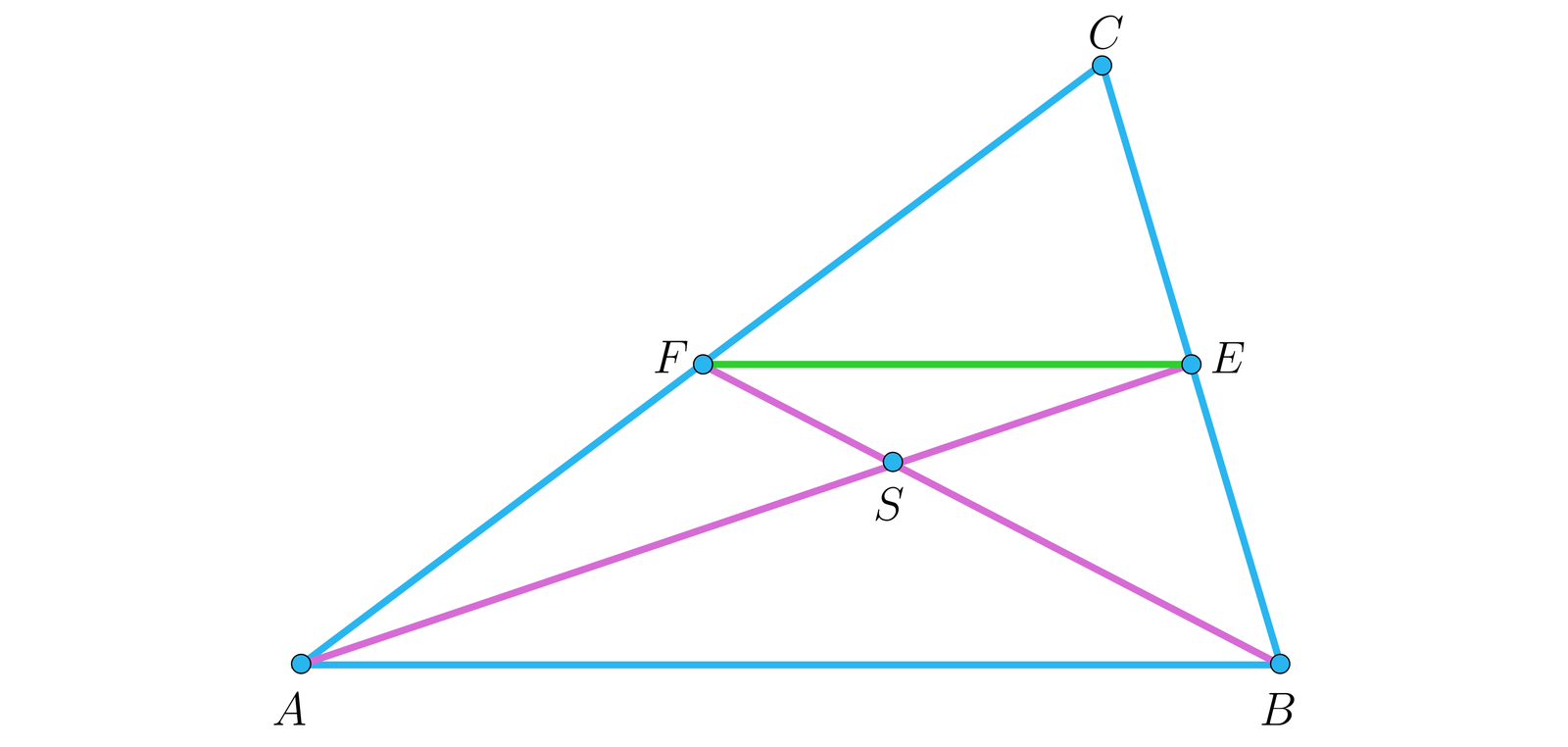
Ponieważ punkt jest punktem przecięcia środkowych w trójkącie , to: i .
Odcinek łączy środki boków i , zatem .
Stąd trójkąty i są podobne w skali . A z własności skali podobieństwa: stosunek pól tych trójkątów wynosi .
Środkowe i trójkąta są prostopadłe, , . Wyznaczymy długości boków trójkąta .
Rozwiązanie
Popatrzmy na rysunek.
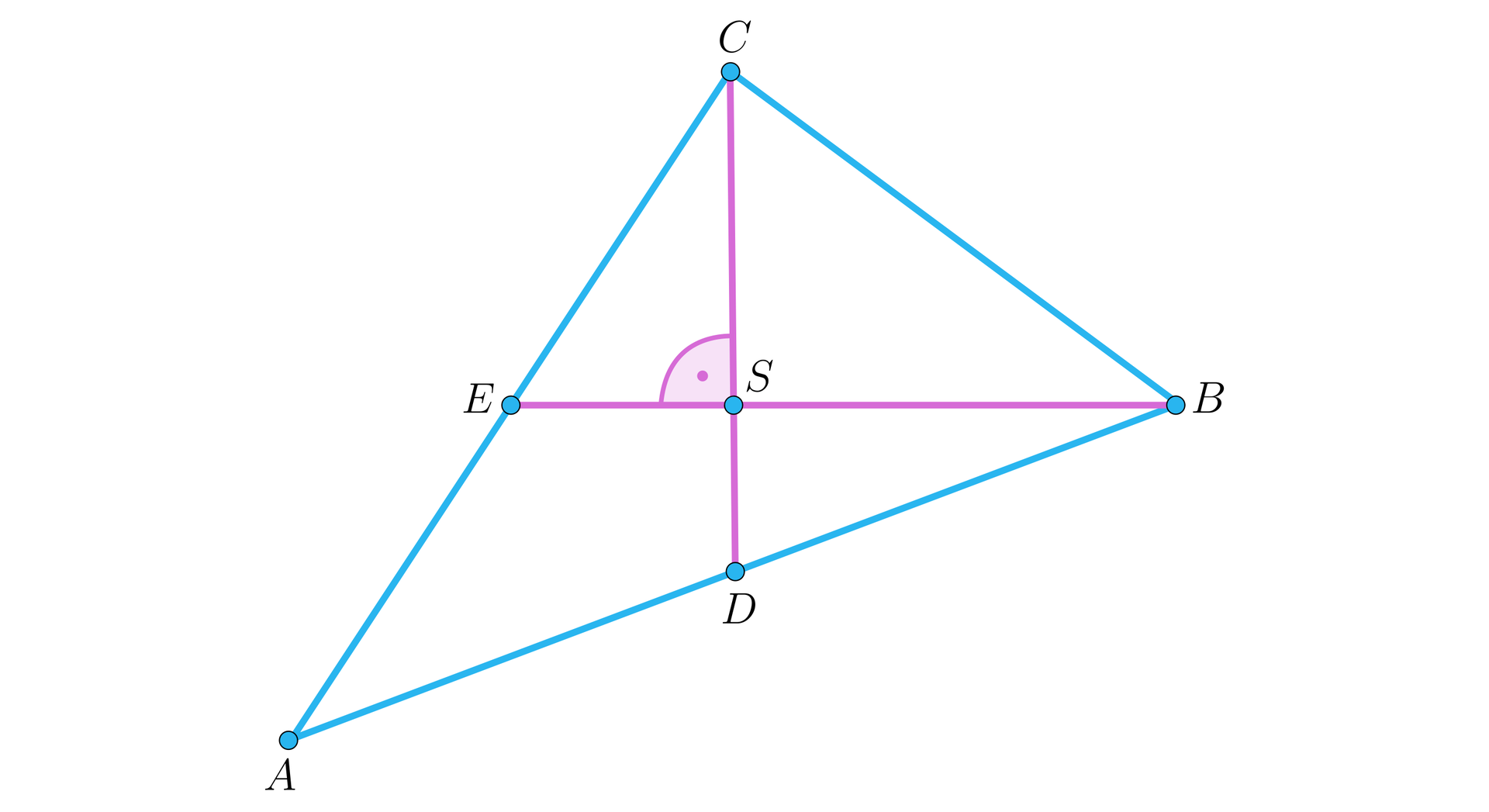
Ponieważ dzieli środkowe w stosunku , to:
Zastosujemy twierdzenie Pitagorasa do obliczenia długości odpowiednich odcinków:
, więc i stąd
, więc
, więc i stąd
Pokażemy, że środkowa poprowadzona z wierzchołka kąta prostego w trójkącie prostokątnym ma długość równą połowie długości przeciwprostokątnej.
Rozwiązanie
Wykorzystujemy fakt, że kąt oparty na średnicy okręgu jest kątem prostym. Środkowa poprowadzona z wierzchołka kąta prostego łączy punkt na okręgu ze środkiem średnicy, czyli ze środkiem okręgu. Stąd mamy, że długość środkowej jest równa długości promienia okręgu, czyli połowie średnicy.
Środek ciężkości trójkąta
Punkt przecięcia środkowych trójkąta, ze względu na analogie fizyczne, nazywany jest środkiem ciężkości (barycentrum) tego trójkąta.
Sprawdź to sam
Aby zobaczyć te analogie wykonaj sam lub w parze następujące doświadczenie.
Narysuj na kartonie dowolny trójkąt.
Wyznacz punkt przecięcia dwóch środkowych tego trójkąta. Uwaga! Dla większej dokładności skonstruuj środki dwóch boków.
Wytnij starannie narysowany trójkąt.
Spróbuj ustawić ten trójkąt na czubku ołówka lub długopisu, tak aby czubek podpierał trójkąt w punkcie przecięcia środkowych.
Jeśli wykonałeś dokładnie to zadanie, trójkąt powinien utrzymać się w poziomie.
Kolejne twierdzenie możemy zastosować w sytuacji, gdy znane są współrzędne wierzchołków trójkąta.
Jeżeli wierzchołki trójkąta mają współrzędne , , to środek ciężkości tego trójkąta ma współrzędne .
Współrzędne wierzchołków trójkąta wynoszą , , . Wyznaczymy odległość punktu ciężkościpunktu ciężkości tego trójkąta od wierzchołków , , .
Rozwiązanie
Z powyższego twierdzenia .
Odległości od wierzchołków trójkąta są długościami odcinków:
Słownik
odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku
odcinek, który łączy środki dwóch boków w trójkącie
punkt przecięcia środkowych trójkąta