Przeczytaj

Na rysunku przedstawiony jest czworokąt $A B C D$ z zaznaczonymi kątami, bokami i przekątnymi.

R1Y7vCwuzVjck

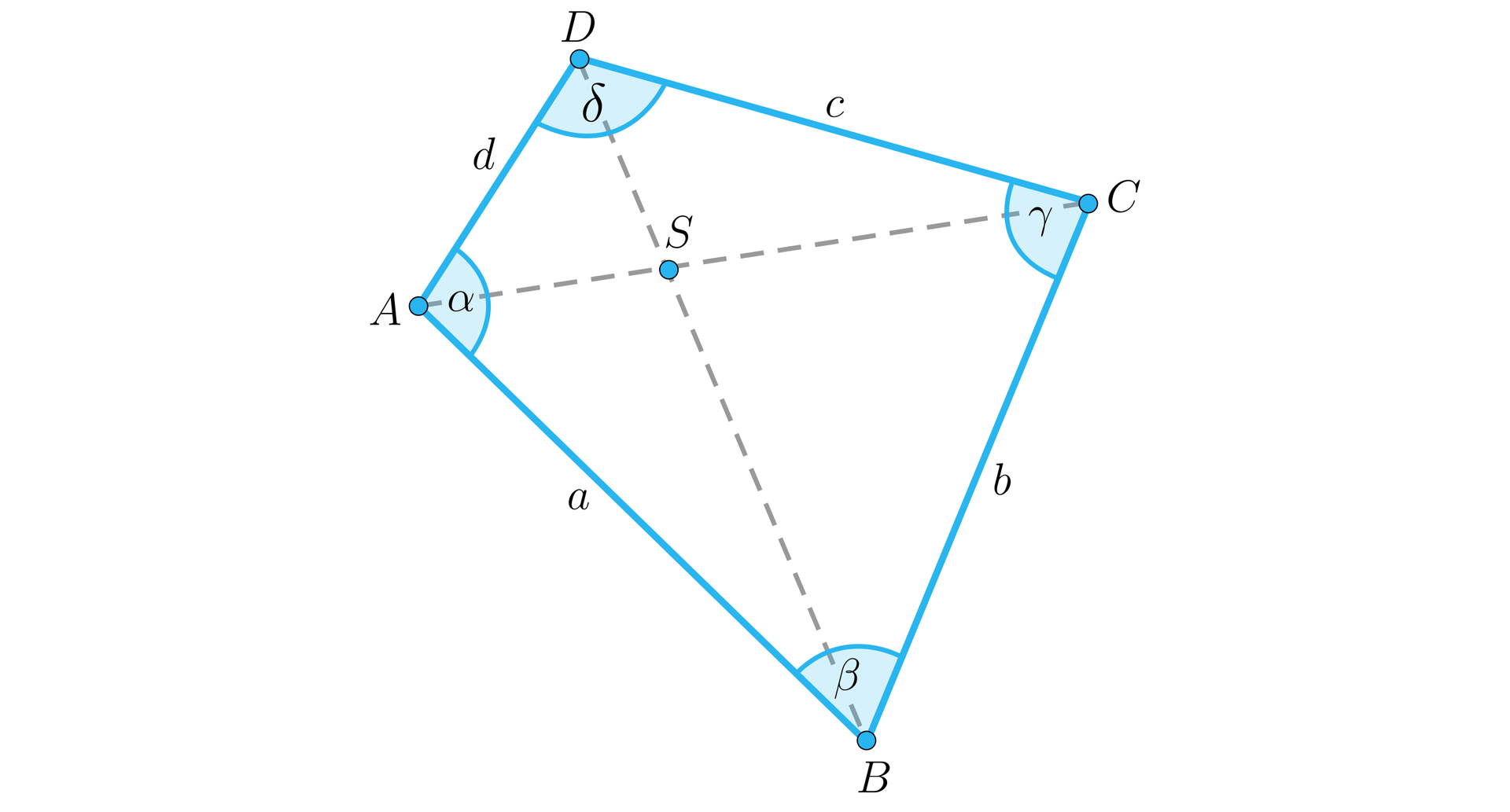
Na ilustracji przedstawiono czworokąt ABCD. Kąt przy wierzchołku A oznaczono alfa, kąt przy wierzchołku B oznaczono beta, kąt przy wierzchołku C oznaczono gamma, kąt przy wierzchołku D oznaczono delta. Linią przerywaną zaznaczono przekątne BD, oraz AC czworokąta. Przekątne przecinają się w punkcie S. Długość boku AB jest równa a, długość boku BC jest równa b, długość boku CD jest równa c, oraz długość boku AD jest równa d.

Jeśli wierzchołki leżą na jednym boku, to mówimy, że są sąsiednie, w przeciwnym przypadku – są przeciwległe.

Boki, które mają wspólny wierzchołek, nazywamy bokami sąsiednimi; w przeciwnym przypadku – przeciwległymi.

Kąty $α$ , $β$ , $γ$ , $δ$ nazywamy kątami wewnętrznymi (lub krócej: kątami) czworokąta.

Jeśli dwa kąty mają wspólne ramię (bok czworokąta), to są kątami sąsiednimi; w przeciwnym przypadku – przeciwległymi.

Kąt jest wypukłykąt wypukłyKąt jest wypukły, jeśli ma miarę mniejszą lub równą $180 °$ .

Czworokąt jest wypukły, gdy jego wszystkie cztery kąty wewnętrzne są wypukłe.

W czworokącie wypukłym przekątne przecinają się w punkcie leżącym wewnątrz czworokąta.

deltoid

Definicja: deltoid

Deltoidem nazywamy wypukły czworokąt, który ma dwie pary sąsiednich boków równych.

Na rysunku przedstawiono czworokąty z zaznaczonymi parami boków równych. Niebieskie czworokąty są deltoidami, a zielone – nie są deltoidami.

R9tTlQ9xZzU8P

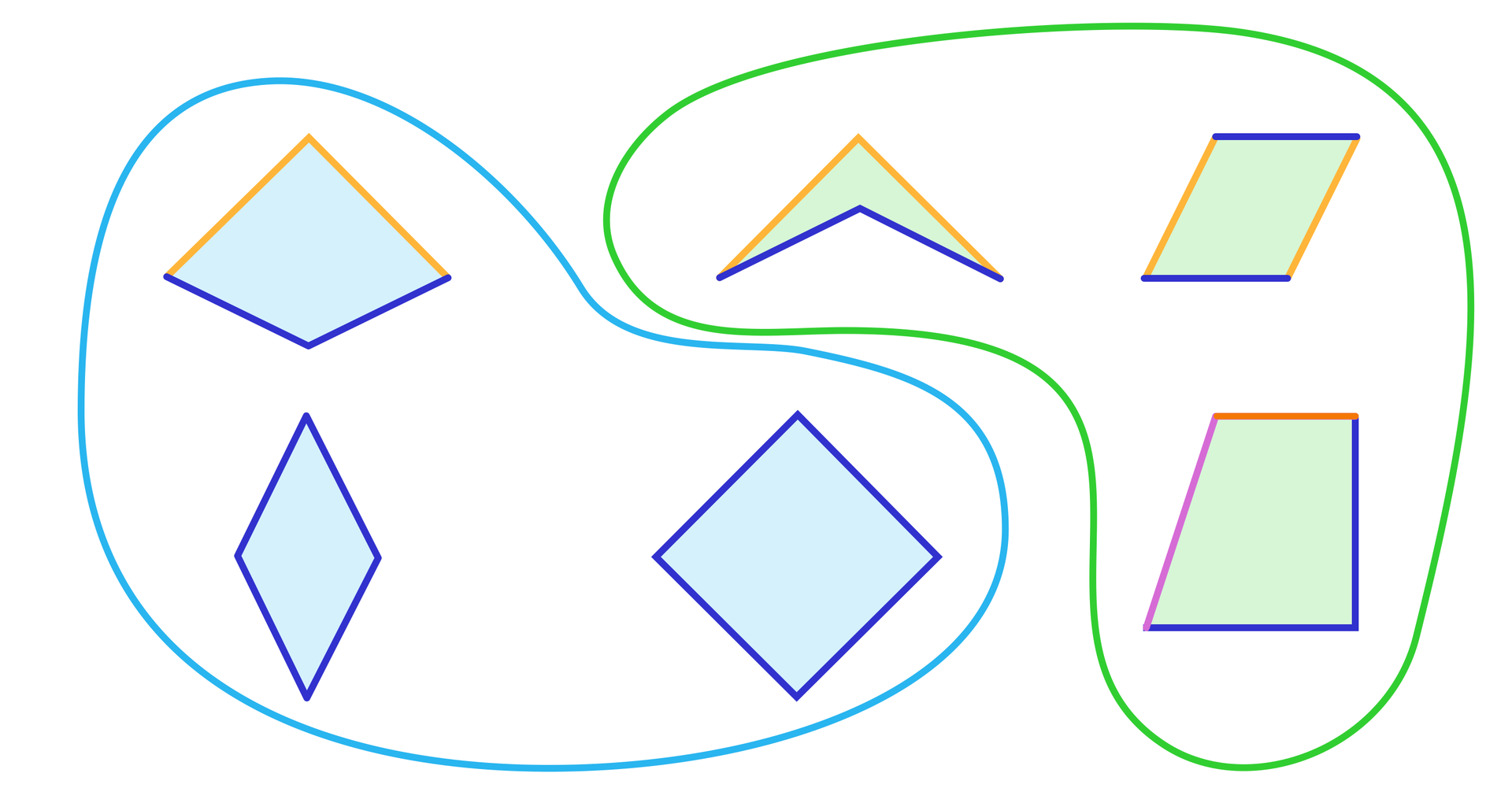
Na ilustracji przedstawiono dwa zbiory figur, które oddzielono pętlami. W pierwszej pętli znajdują się trzy czworokąty, między innymi romb i czworokąt. W pętli drugiej znajdują się również trzy czworokąty, między innymi trapez i równoległobok.

Zielony czworokąt deltoidalnyczworokąt deltoidalnyczworokąt deltoidalny ma dwie pary sąsiednich boków równych, ale nie jest wypukły.

Zielony równoległobok ma dwie pary boków równych, ale nie są to boki sąsiednie.

Zielony trapez ma jedną parę sąsiednich boków równych.

RombrombRomb jest deltoidem, bo ma wszystkie boki równe. KwadratkwadratKwadrat jest deltoidem, bo jest rombem.

Własności deltoidów

Popatrzmy na rysunek przedstawiający deltoiddeltoiddeltoid.

RRE3q5XYI2fSF

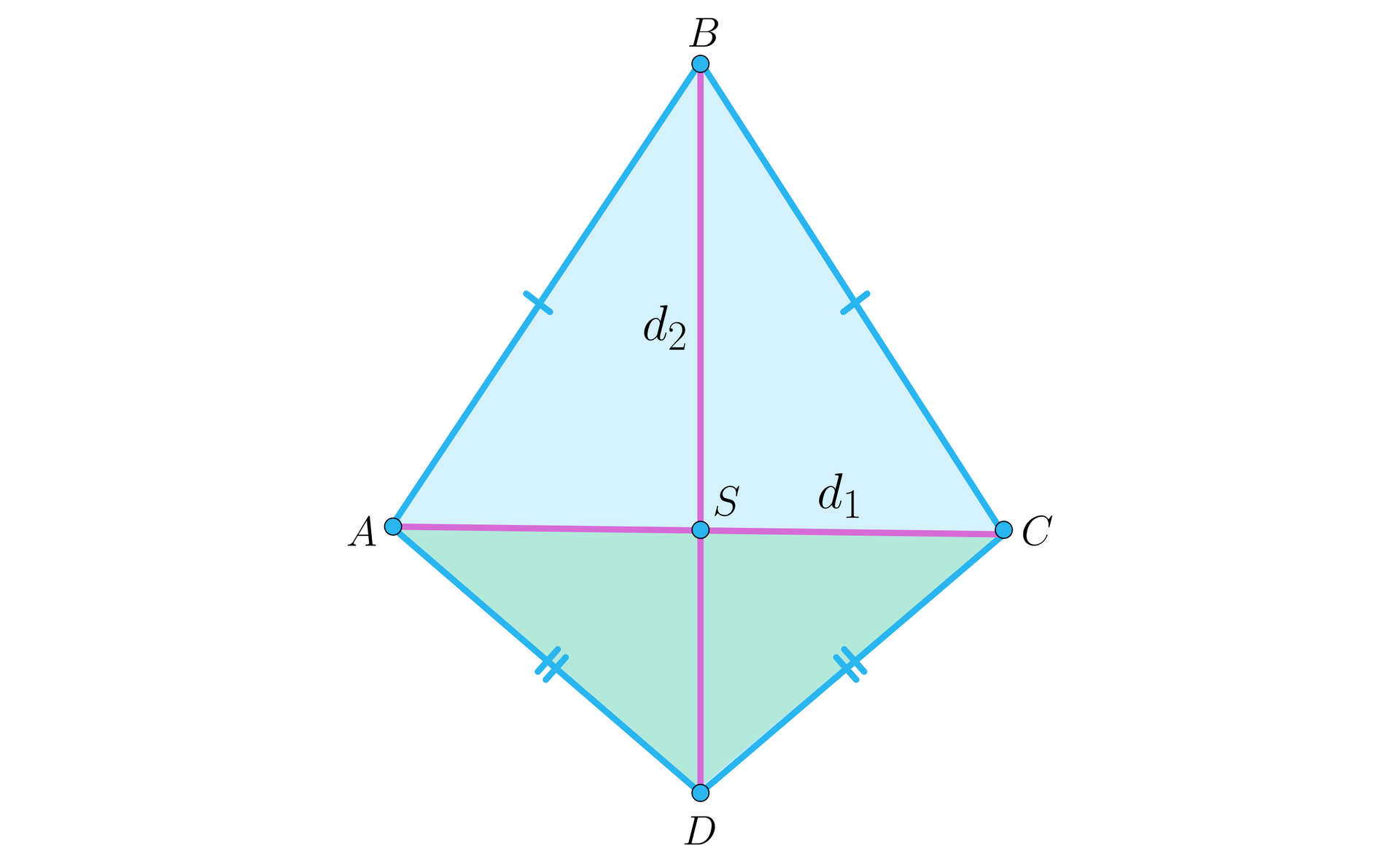
Na ilustracji przedstawiono deltoid ABCD. Długość boku AB jest równa długości boku BC, oraz długość boku AD jest równa długości boku CD. Zaznaczono przekątną d1 łączącą wierzchołki A i C, oraz przekątną d2 łączącą wierzchołki B i D. Przekątne przecinają się w punkcie S.

Ponieważ deltoid ma dwie pary sąsiednich boków równych, to każda z par tworzy ramiona trójkąta równoramiennego o podstawie, która jest przekątną $A C$ deltoidu.

Zauważmy, że wysokości w tych trójkątach leżą na symetralnej podstawy $A C$ i przekątna $B D$ deltoidu jest sumą wysokości tych trójkątów.

Dla uproszczenia zapisu przyjmijmy, że w deltoidzie:

przekątna, która dzieli deltoid na trójkąty równoramienne, oznaczana jest symbolem $d_{1}$ ,
przekątna, która jest sumą wysokości tych trójkątów równoramiennych, oznaczana jest symbolem $d_{2}$ .

Przykład 1

Pokażemy, że przekątna $d_{2}$ leży na symetralnej przekątnej $d_{1}$ oraz, że przekątne deltoidu przecinają się pod kątem prostym i przekątna $d_{2}$ dzieli przekątną $d_{1}$ na połowy.
Pokażemy, że przekątna $d_{2}$ w deltoidzie jest dwusieczną kątów leżących przy wierzchołkach, które ona łączy.

RHHCMHljYfrAx

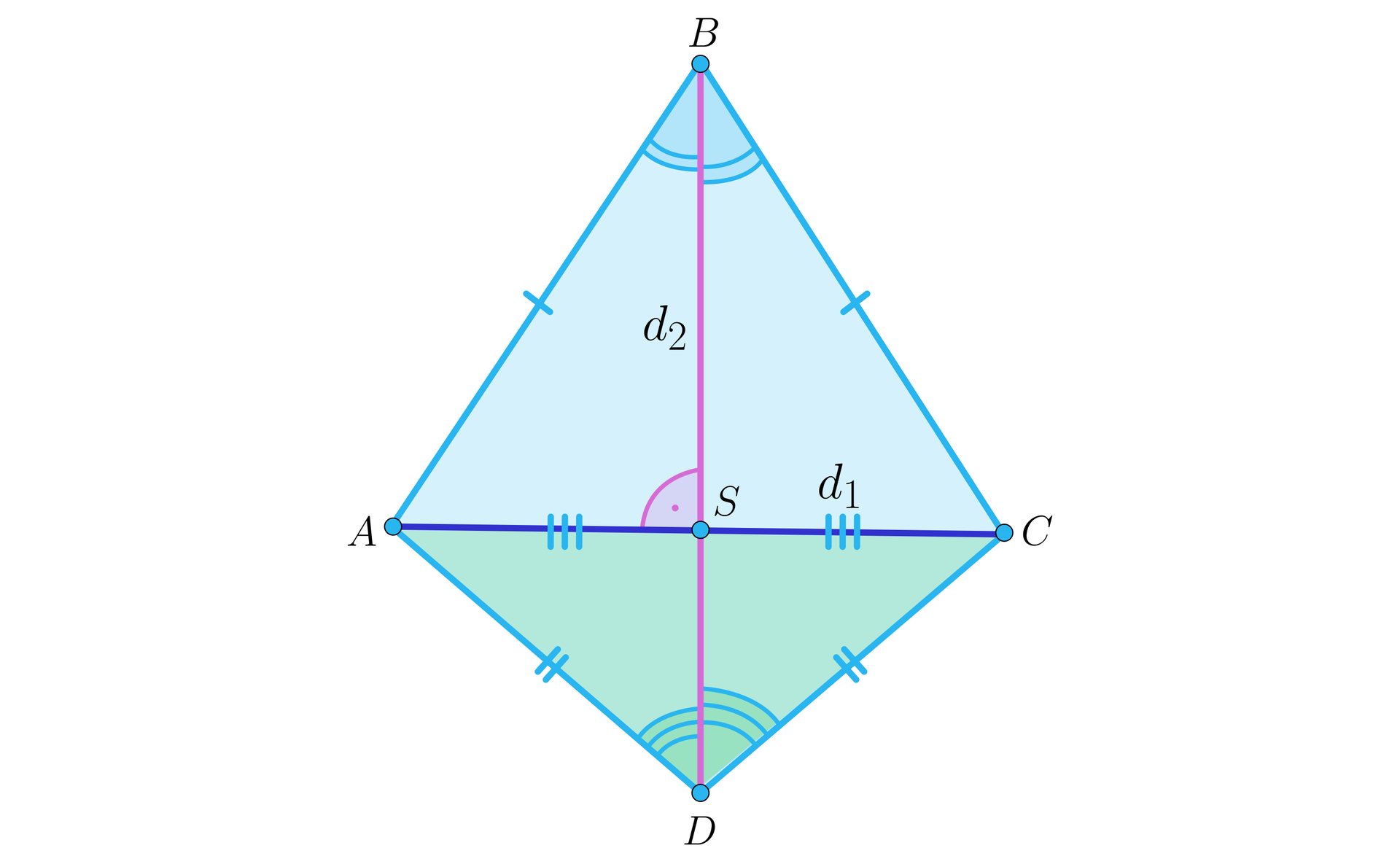
Rozwiązanie

Rzeczywiście, wystarczy zauważyć, że w trójkącie równoramiennym dwusieczna kąta leżącego naprzeciwko podstawy oraz wysokość poprowadzona do podstawy leżą na symetralnej podstawy.

Charakteryzacja deltoidu

Własność: Charakteryzacja deltoidu

Czworokąt wypukłyczworokąt wypukłyCzworokąt wypukły jest deltoidem wtedy i tylko wtedy, gdy jedna z przekątnych jest symetralną drugiej przekątnej.

Czworokąt wypukły jest deltoidem wtedy i tylko wtedy, gdy jedna z przekątnych leży na dwusiecznej kątów przy wierzchołkach, które łączy.

Czworokąt wypukły jest deltoidem wtedy i tylko wtedy, gdy jedna z przekątnych jest jego osią symetrii.

Dowód

Jeśli czworokąt jest deltoidem, to przekątna $d_{2}$ leży na symetralnej przekątnej $d_{1}$ .
W drugą stronę, odwołajmy się do własności symetralnej odcinkasymetralna odcinkasymetralnej odcinka:
Symetralna odcinka jest zbiorem punktów równoodległych od końców tego odcinka.
Załóżmy, że jedna przekątna czworokąta wypukłego $A B C D$ , na przykład $B D$ , leży na symetralnej przekątnej $A C$ . Z własności symetralnej wynika, że $|A B| = |B C|$ i $|A D| = |D C|$ , więc czworokąt $A B C D$ jest deltoidem.

Jeśli czworokąt jest deltoidem, to przekątna $d_{2}$ leży na dwusiecznej kątówdwusieczna kątadwusiecznej kątów leżących naprzeciwko przekątnej $d_{1}$ .
W drugą stronę, załóżmy, że jedna przekątna czworokąta wypukłego $A B C D$ , na przykład $B D$ , jest dwusieczną kątów przy wierzchołkach $B$ i $D$ . Wtedy z cechy przystawania trójkątów kbk wynika, że trójkąty $A B D$ i $C B D$ są przystające, więc mają równe wysokości opuszczone na wspólną podstawę $B D$ .
R1W1ifBZ4HdEq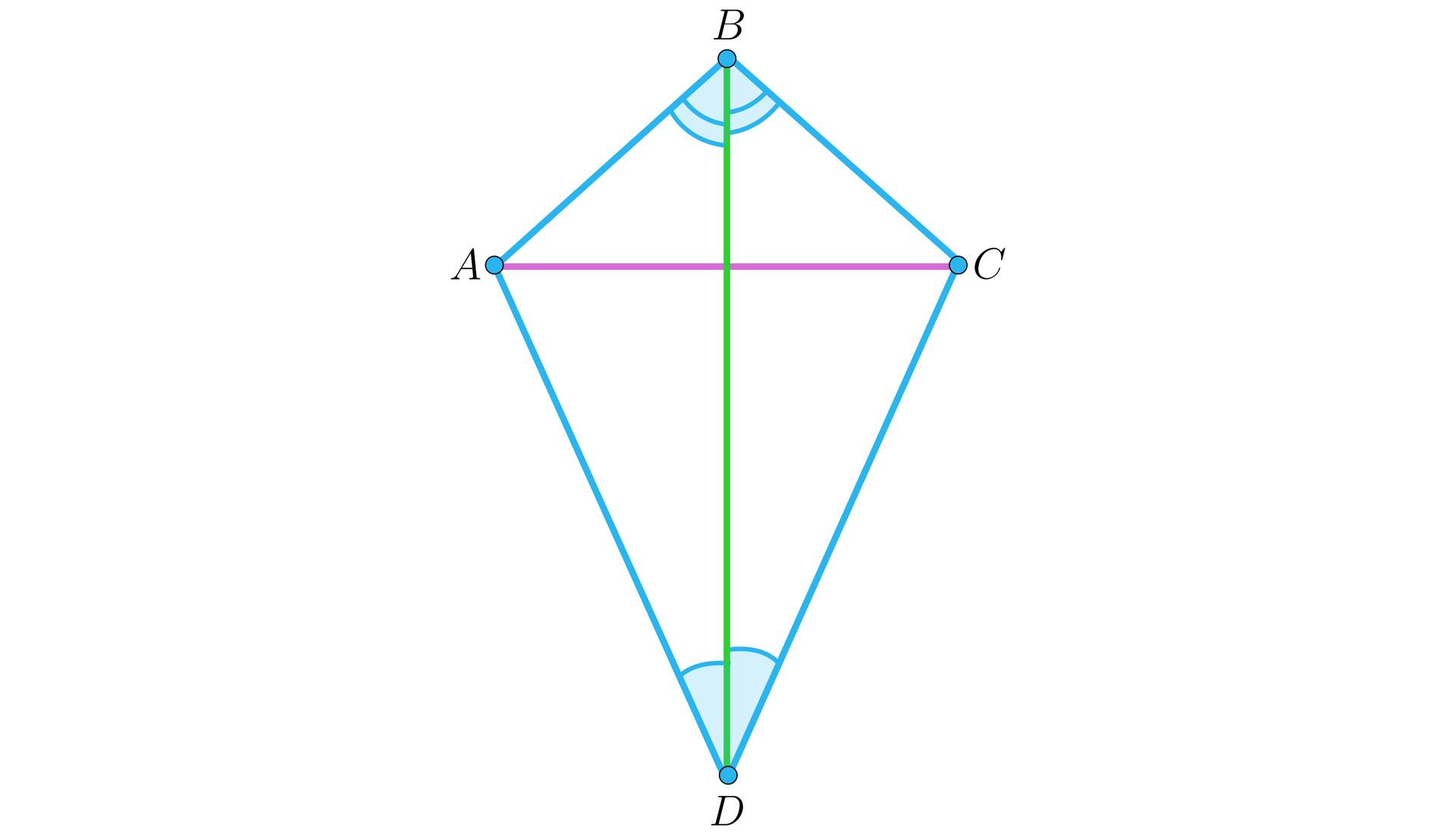

Jeśli przekątna leży na osi symetrii czworokąta, to jest dwusieczną kątów przy wierzchołkach będącymi końcami tej przekątnej, a stąd własność $3$ jest prawdziwa.

Przykład 2

Wskażemy w deltoidzie pary trójkątów przystających. Zastosujmy oznaczenia z powyższego rysunku i niech $S$ będzie punktem przecięcia przekątnych deltoidu.

RF9J8b5DqLm6h

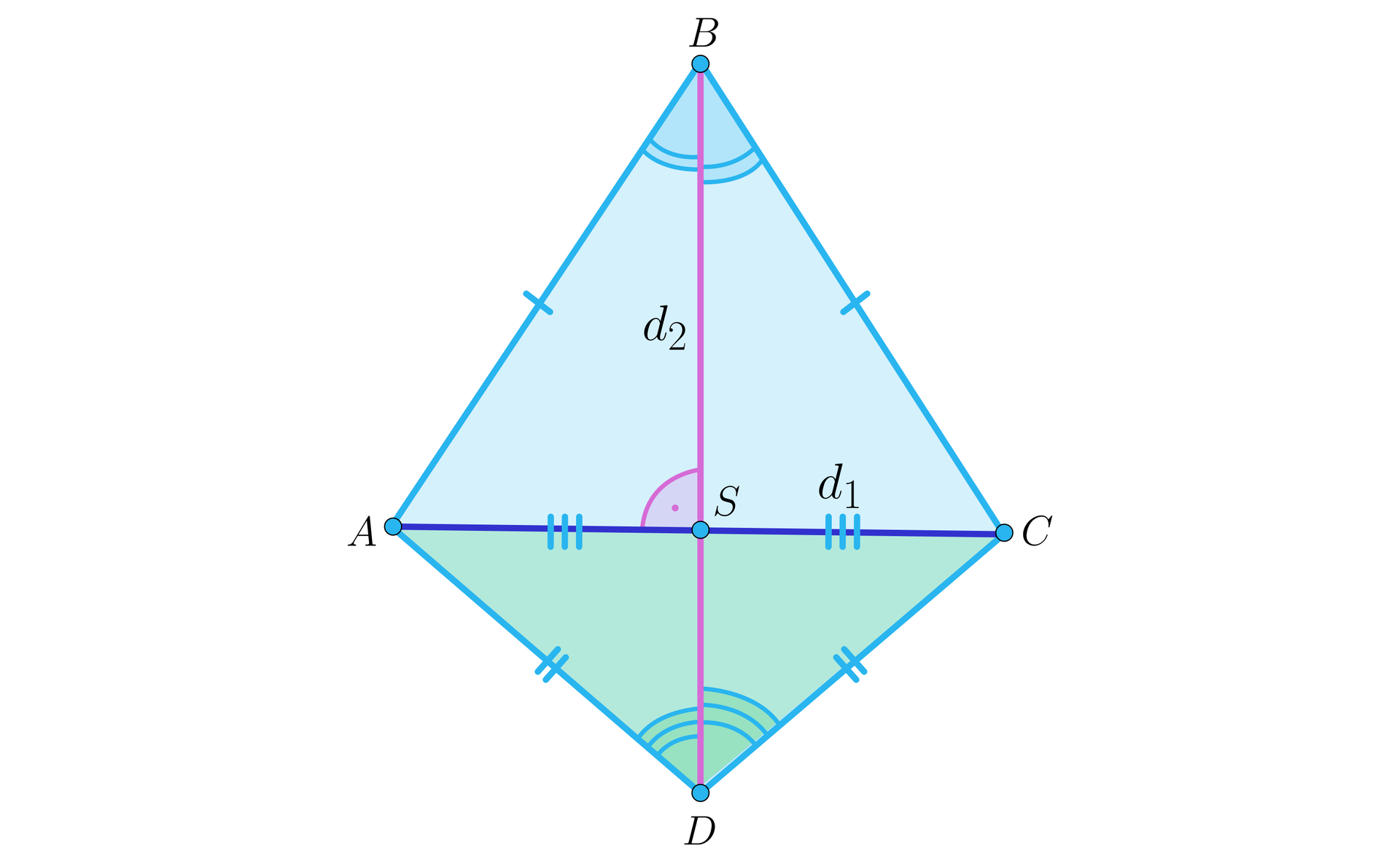
Rozwiązanie

Trójkąty $A B D$ i $C B D$ są przystające na mocy cechy kbk, bo mają wspólny bok $B D$ i równe odpowiednie kąty leżące przy tym boku. Również cecha bbb dowodzi przystawania tych trójkątów.

Trójkąty $A B S$ i $C B S$ są przystające, zarówno na mocy cechy bbb jak i cechy kbk.

Podobnie, trójkąty $A D S$ i $C D S$ są przystające na mocy obu tych cech

równość kątów w deltoidzie

Własność: równość kątów w deltoidzie

Dwa kąty przy wierzchołkach, które łączy przekątna $d_{1}$ , są równe.

Dowód

Własność ta wynika wprost z faktu, że przekątna $d_{2}$ leży na osi symetrii deltoidu.

Przykład 3

Powtórzmy fragment instrukcji budowy latawca.

Weź dwie drewniane listewki. Przytnij listewki do odpowiedniej długości. Krótsza z nich powinna mieć długość równą $\frac{3}{4}$ długości dłuższej listewki.
Wyznacz dokładny środek krótszej z listewek i zwiąż listewki ze sobą sznurkiem na kształt krzyża (pod kątem $90 °$ ). Krótsza listwa powinna znajdować się na wysokości około $\frac{2}{3}$ dłuższej listewki.
Wiązanie wzmocnij za pomocą kleju. Pamiętaj, że musi być zachowany dokładny kąt $90 °$ – inaczej latawiec nie będzie latał.

Pokażemy, że instrukcja ta wskazuje jak zbudować przekątne deltoidu, który nie jest rombem.

Wyznaczymy też obwód tego latawca przy założeniu, że $d_{2} = 96 cm$ .

Rozwiązanie

Rzeczywiście, po pierwsze, krótsza przekątna ma długość $\frac{3}{4}$ długości dłuższej. Po drugie, punkt przecięcia jest na wysokości $\frac{2}{3}$ dłuższej przekątnej i w połowie krótszej przekątnej, czyli krótsza przekątna dzieli się w połowie. Ostatecznie, przekątne przecinają się pod kątem prostym.

Obliczamy $d_{1} = \frac{3}{4} d_{2} = \frac{96 \cdot 3}{4} = 72 cm$ . Niech $S$ będzie punktem przecięcia przekątnych.

Rw5MSlcgbWLJZ

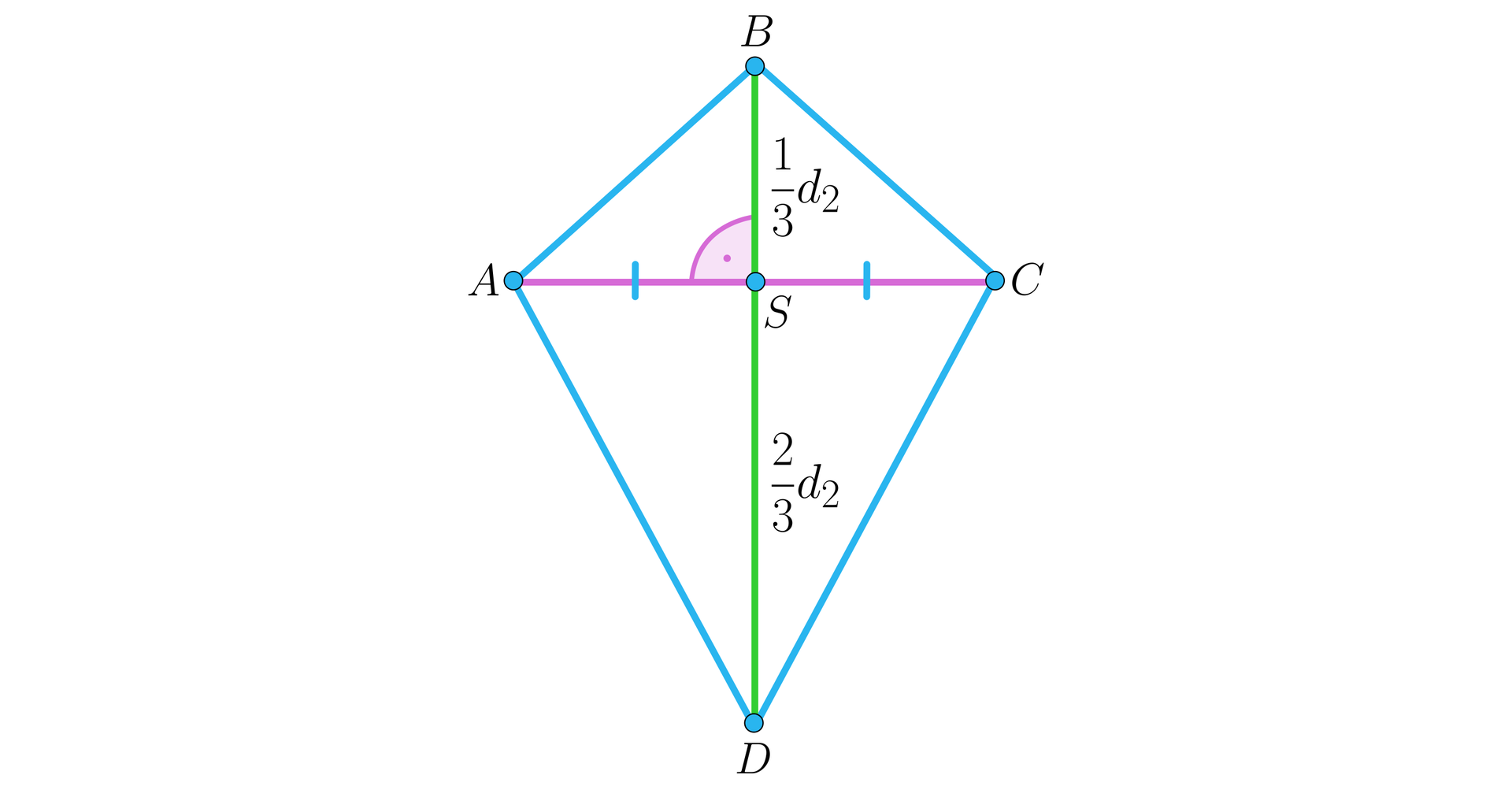
Na ilustracji przedstawiono deltoid ABCD. Zaznaczono przekątne AC i BD. Przekątna BD jest dwusieczną kątów leżących przy wierzchołkach, które ona łączy. Przekątna AC przecina przekątną BD w punkcie S i pod kątem prostym. Punkt S dzieli przekątną AC na dwie równe części, natomiast przekątną BD w stosunku jeden do trzech.

Wtedy $|B S| = \frac{96}{3} = 32 cm$ , $|S D| = \frac{96 \cdot 2}{3} = 64 cm$ ,

$|A S| = |C S| = 36 cm$ .

Aby wyznaczyć obwód tego deltoidu trzeba wyznaczyć długości boków $A B$ i $A D$ . Skorzystamy z twierdzenia Pitagorasa.

${|A B|}^{2} = 36^{2} + 32^{2} = 2320$ , $|A B| = \sqrt{2320} = 4 \sqrt{145} cm$

${|A D|}^{2} = 64^{2} + 36^{2} = 5392$ , $|A D| = \sqrt{5392} = 4 \sqrt{337} c m$

Obwód deltoidu jest równy $8 \sqrt{145} + 8 \sqrt{337}$ centymetrów.

Pole deltoidu

Aby wyznaczyć pole deltoidu skorzystamy z umiejętności obliczania pól trójkątów prostokątnych. Przy oznaczeniach z rysunku zauważamy, że deltoid jest sumą trójkątów $A B C$ i $A D C$ , więc pole deltoidu jest sumą pól tych trójkątów.

R1EzoM7keoZQD

$P_{A B C D} = P_{A B C} + P_{A D C} = \frac{|B S| \cdot |A C|}{2} + \frac{|D S| \cdot |A C|}{2} = \frac{|A C|}{2} (|B S| + |D S|) = \frac{d_{1} \cdot d_{2}}{2}$

Pokazaliśmy w ten sposób następujące twierdzenie

o polu deltoidu 1

Twierdzenie: o polu deltoidu 1

Pole deltoidu o przekątnych $d_{1}$ i $d_{2}$ jest równe $P = \frac{d_{1} \cdot d_{2}}{2}$ .

Przykład 4

Policzymy pole deltoidu wiedząc, że jego przekątne mają długości $72$ i $96$ centymetrów.

Rozwiązanie

$P = \frac{72 \cdot 96}{2} = 3456 {cm}^{2}$

Zauważmy, że deltoid jest również sumą trójkątów $A B D$ i $C B D$ , więc pole deltoidu jest sumą pól tych trójkątów. Wiemy, że te trójkąty są przystające, więc

$P_{A B C D} = P_{A B D} + P_{C B D} = 2 P_{A B D}$

R1U3ibLnL4JYo

Na ilustracji przedstawiono deltoid ABCD. Zaznaczono dłuższą przekątna d2, łączącą wierzchołek B i D. Przy wierzchołku A zaznaczono kąt alfa. Bok AB oznaczono małą literą a, natomiast bok AD oznaczono małą literą d.

Stąd wynika, że do policzenia pola deltoidu wystarczy znać pole trójkąta, którego bokiem jest przekątna $d_{2}$ . Jeśli znamy długości pozostałych boków $a = |A B|$ , $b = |A D|$ oraz kąt $α$ między tymi bokami, to otrzymujemy następujące twierdzenie:

o polu deltoidu 2

Twierdzenie: o polu deltoidu 2

Pole deltoidu jest równe $P = a b \sin α$ , gdzie $a$ , $b$ są długościami boków przy jednym z wierzchołków, które łączy przekątna $d_{1}$ a kąt $α$ jest kątem między tymi bokami.

Przykład 5

Obliczymy pole deltoidu przy założeniu, że $α = 120 °$ , $|A B| = 5$ , $|A D| = 10$

Rozwiązanie

$P = 5 \cdot 10 \cdot \sin 120 ° = \frac{50 \sqrt{3}}{2} = 25 \sqrt{3}$ .

Porównanie własności deltoidu i wklęsłego czworokąta deltoidalnego

Czworokąt, który ma dwie pary sąsiednich boków równych, ale nie jest wypukły, nazywany jest wklęsłym czworokątemczworokąt wklęsływklęsłym czworokątem deltoidalnym.

Na rysunku przedstawiony jest wklęsły czworokąt deltoidalny.

R179xppkxbBhm

Na ilustracji przedstawiono trójkąt równoramienny ABC. Na około jednej drugiej wysokości trójkąta, opuszczonej z wierzchołka B do podstawy, zaznaczono punkt D. Powstał czworokąt ABCD, zwany wklęsłym czworokątem deltoidalnym. Zaznaczono również odcinek BD.

Własności wspólne dla omawianych czworokątów to:

Jedna z przekątnych leży na symetralnej drugiej przekątnej.
Jedna z przekątnych leży na dwusiecznej kątów przy wierzchołkach, z których wychodzi.
Jedna z przekątnych leży na jego osi symetriioś symetrii figuryosi symetrii.

W poniższej tabeli zaznaczone są różnice między omawianymi czworokątami.

Deltoid	Wklęsły czworokąt deltoidalny
Przekątne przecinają się	Przekątne nie przecinają się
Jedna z przekątnych dzieli drugą w połowie pod kątem prostym	Linia zawierająca jedną z przekątnych dzieli drugą w połowie pod kątem prostym
Jest sumą trójkątów równoramiennych	Jest różnicą trójkątów równoramiennych

Słownik

kąt wypukły

kąt, który ma miarę mniejszą lub równą $180 °$

czworokąt wypukły

czworokąt, którego wszystkie cztery kąty wewnętrzne są wypukłe

czworokąt wklęsły

czworokąt, którego jeden z kątów wewnętrznych jest wklęsły

kwadrat

czworokąt, który ma wszystkie boki równe i wszystkie kąty proste

romb

czworokąt, który ma wszystkie boki równe

deltoid

czworokąt wypukły, który ma dwie pary równych boków sąsiednich

czworokąt deltoidalny

czworokąt, który ma dwie pary równych boków sąsiednich

symetralna odcinka

prosta prostopadła do danego odcinka przechodząca przez jego środek

dwusieczna kąta

prosta dzieląca ten kąt na dwa równe kąty

oś symetrii figury

prosta, względem której ta figura jest do siebie osiowo symetryczna

Wprowadzenie

Aplet

Własności deltoidów

Pole deltoidu

Porównanie własności deltoidu i wklęsłego czworokąta deltoidalnego

Słownik