Przeczytaj

Dowody dotyczące pola figur opierają się na ważnych własnościach pola.

Własności pola figury

Własność: Własności pola figury

Niech $P_{F}$ oznacza pole figury $F$ . Wówczas możemy wyróżnić trzy ważne właśności.

Figury przystające mają równe pola.
Jeżeli figura $F_{1}$ jest zawarta w figurze $F_{2}$ to $P_{F_{1}} \leq P_{F_{2}}$ .
Jeżeli $F_{1}$ , $F_{2}$ są rozłączne, to pole ich sumy jest równe sumie pól. W ogólności, pole sumy figur jest równe sumie ich pól minus pole ich części wspólnej.

Przykład 1

W trapezie równoramiennymtrapez równoramiennytrapezie równoramiennym $A B C D$ każda przekątna ma długość $12$ . Przekątne przecinają się pod kątem $120 °$ i dzielą się w stosunku $2 : 1$ . Wyznaczymy pole tego trapezutrapeztrapezu.

Rozwiązanie

W trójkącie $D S C$ dwa boki są równe: $|D S| = |C S| = \frac{d}{3} = 4$ .

R1bCacxHvQtiA

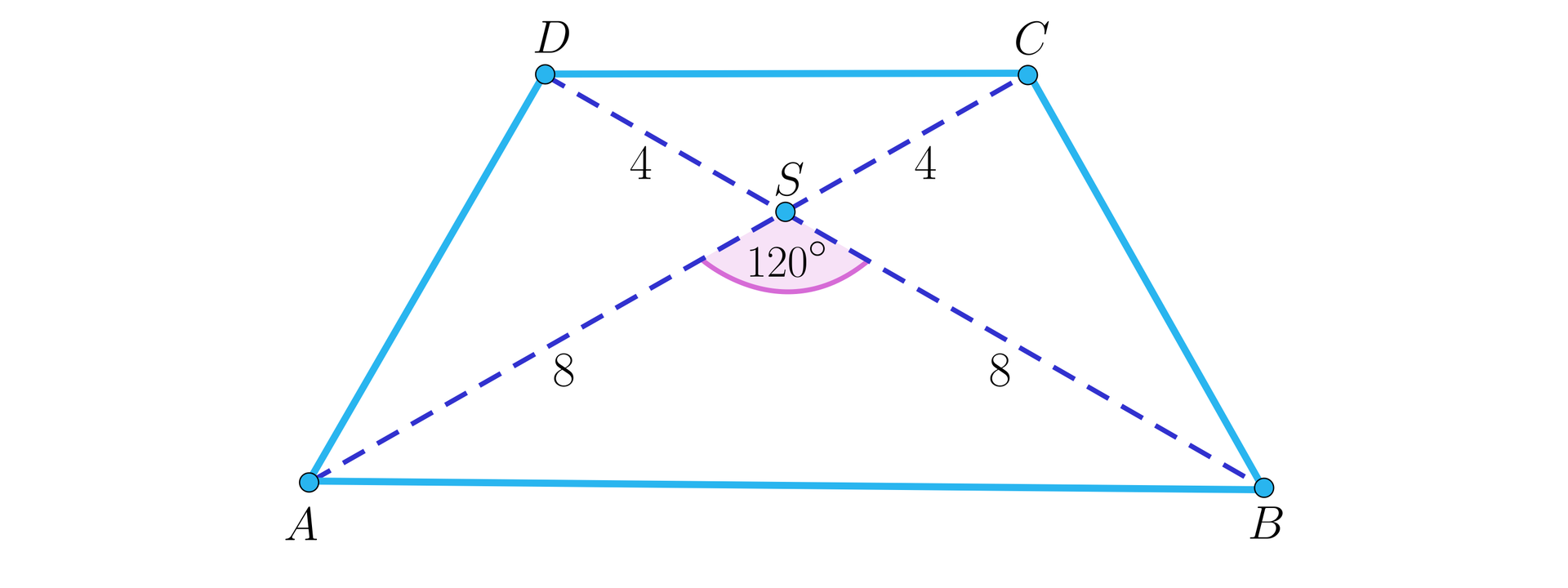
Ilustracja przedstawia trapez równoramienny ABCD. Jego przekątne przecinają się w punkcie S. Przekątne mają długość 12 i dzielą się na dwa odcinki 4 i osiem. Kąt między przekątnymi wynosi 120 stopni.

Stąd pole trójkąta $D S C$ jest równe $\frac{1}{2} \cdot 4 \cdot 4 \cdot \sin 120 ° = \frac{8 \sqrt{3}}{2} = 4 \sqrt{3}$ .

Pole trójkąta $A S B$ jest $4$ razy większe od pola trójkąta $D C S$ , bo trójkąty te są podobne w skali $2 : 1$ . Zatem pole trójkąta $A S B$ jest równe $16 \sqrt{3}$ .

Trójkąt $A S D$ ma boki długości:

$|A S| = \frac{2 d}{3} = 8$ , $|D S| = \frac{d}{3} = 4$ oraz kąt $∢ A S D = \frac{360 ° - 2 \cdot 120 °}{2} = 60 °$ .

Stąd pole trójkąta $A S D$ jest równe $\frac{1}{2} \cdot 8 \cdot 4 \cdot \sin 60 ° = \frac{16 \sqrt{3}}{2} = 8 \sqrt{3}$ .

Ostatecznie pole trapezu $A B C D$ jest równe $4 \sqrt{3} + 16 \sqrt{3} + 2 \cdot 8 \sqrt{3} = 36 \sqrt{3}$ .

o długości odcinka łączącego środki przekątnych trapezu

Twierdzenie: o długości odcinka łączącego środki przekątnych trapezu

W trapezie o podstawach długości $a$ , $b$ odległość między środkami przekątnych wyraża się wzorem $\frac{a - b}{2}$ .

Dowód

RSEe0xmDIctnU

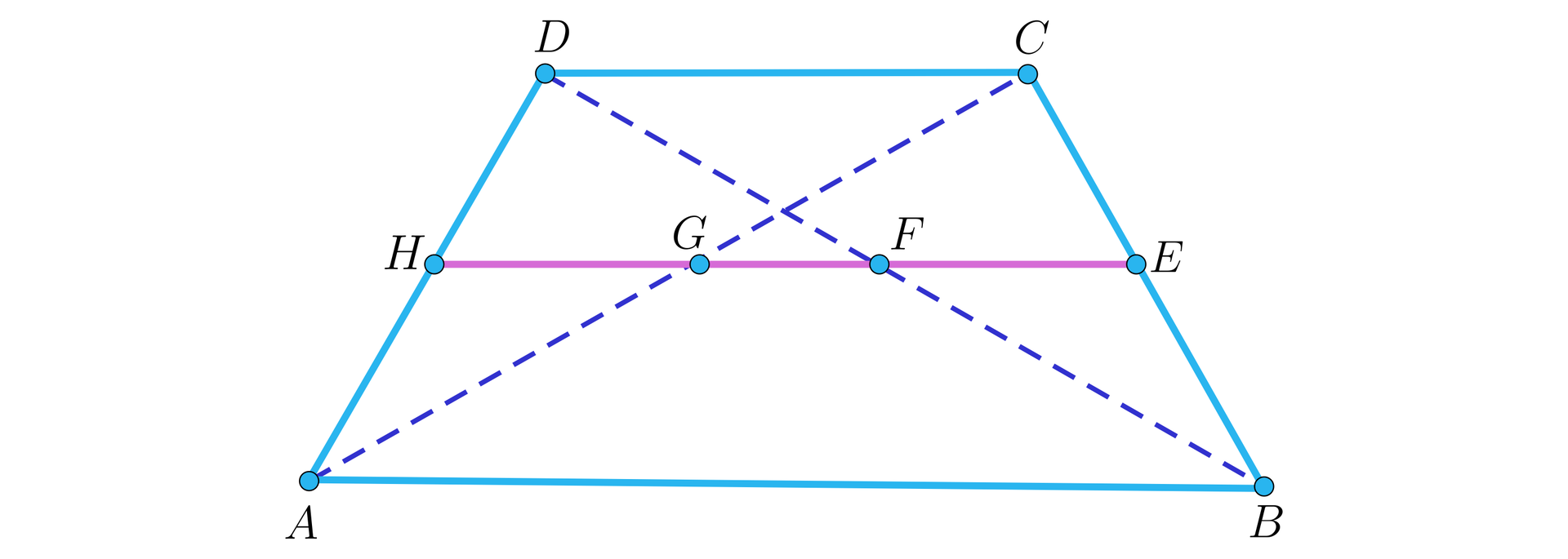
Ilustracja przedstawia trapez równoramienny ABCD. Zaznaczono przekątne AC i BD. Na środkach ramion zaznaczono punkty H i E tworzące odcinek przecinający przekątne w punkcie G i F.

Przyjmujemy oznaczenia: $|A B| = a$ oraz $|C D| = b$ . Zauważmy, że na odcinku $E H$ leżą środki przekątnych trapezu, więc jest to jego linia środkowa. Wynika stąd, że odcinek $E H$ łączy środki ramion $A D$ oraz $B C$ . Zatem $|A H| = \frac{|A D|}{2}$ , $|B E| = \frac{|B C|}{2}$ , $|A G| = \frac{|A C|}{2}$ , $|B F| = \frac{|B D|}{2}$ oraz $|G F| = |H F| - |H G|$ .

Wyróżnimy dwa trójkąty: $A B D$ oraz $A C D$ .

Zacznijmy od trójkąta $A C D$ . Zauważmy trójkąty $A G H$ i $A C D$ są podobne na mocy cechy podobieństwa $k k k$ . Więc możemy zapisać następującą zależność $\frac{|A H|}{|A D|} = \frac{|H G|}{|C D|}$ , czyli $\frac{1}{2} = \frac{|H G|}{b}$ . Wynika stąd, że $|H G| = \frac{b}{2}$ .

Podobne rozważania przeprowadzamy dla trójkąta $A B D$ . Zauważmy trójkąty $H G D$ i $A B D$ są podobne na mocy cechy podobieństwa $k k k$ . Więc możemy zapisać następującą zależność $\frac{|H D|}{|A D|} = \frac{|H F|}{|A B|}$ , czyli $\frac{1}{2} = \frac{|H F|}{a}$ . Wynika stąd, że $|H F| = \frac{a}{2}$ .

Podsumowując $|G F| = |H F| - |H G| = \frac{a}{2} - \frac{b}{2} = \frac{a - b}{2}$ .

RównoległobokrównoległobokRównoległobok jest trapezem, więc własności przekątnych w trapezie stosują się też do równoległoboku.

o polu równoległoboku

Twierdzenie: o polu równoległoboku

Ra08u0au6QHr3

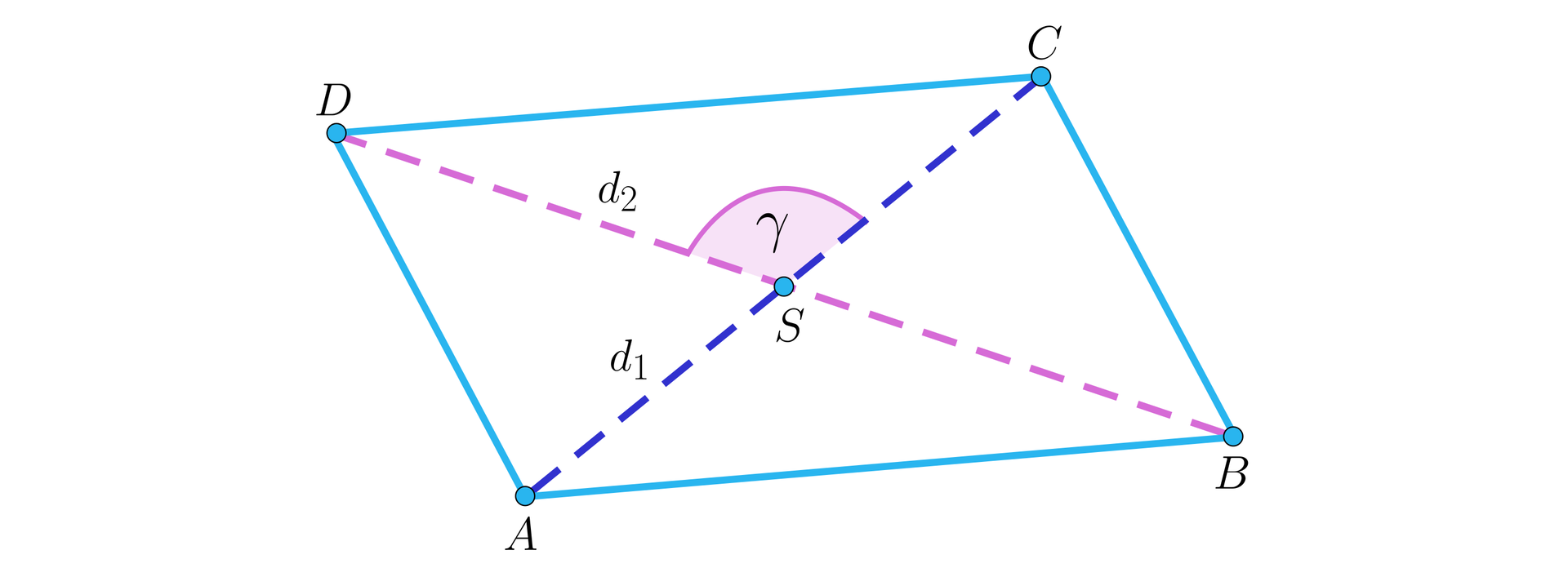
Ilustracja przedstawia równoległobok ABCD. Zaznaczono przekątne d indeks dolny 1 koniec indeksu oraz d indeks dolny 2 koniec indeksu przecinające się w punkcie S. Kąt między przekątnymi wynosi gamma.

Pole równoległoboku o przekątnych $d_{1}$ , $d_{2}$ i kącie $γ$ między przekątnymi jest równe:

P = \frac{d_{1} \cdot d_{2}}{2} \cdot \sin γ

Dowód

Pole równoległoboku $A B C D$ jest równe:

$P = P_{A S B} + P_{C S D} + P_{A S D} + P_{C S B} = 2 P_{A S B} + 2 P_{A S D} =$

$= 2 \cdot \frac{\frac{d_{1}}{2} \cdot \frac{d_{2}}{2}}{2} \sin γ + 2 \cdot \frac{\frac{d_{1}}{2} \cdot \frac{d_{2}}{2}}{2} \cdot \sin (180 ° - γ) = \frac{d_{1} \cdot d_{2}}{4} \cdot (\sin γ + \sin (180 ° - γ)) =$

$= \frac{d_{1} \cdot d_{2}}{4} \cdot 2 \cdot \sin γ = \frac{d_{1} \cdot d_{2}}{2} \cdot \sin γ$

Przykład 2

Przekątne równoległoboku mają długości $14$ i $18$ . Kąt rozwarty między przekątnymi jest $5$ razy większy niż kąt ostry między tymi przekątnymi. Wyznaczymy pole tego równoległoboku.

Rozwiązanie

Niech $α$ będzie miarą kąta ostrego. Wtedy $α + 5 α = 180 °$ , więc $α = \frac{180 °}{6} = 30 °$ .

Zatem $P = \frac{14 \cdot 18}{2} \cdot \sin 30 ° = \frac{14 \cdot 18}{2 \cdot 2} = 63$ .

Przykład 3

Pole równoległoboku o bokach długości $4$ oraz $6$ wynosi $12 \sqrt{3}$ . Wyznaczymy długości przekątnych tego równoległoboku.

Rozwiązanie

Zaczniemy od wyznaczenia miar kątów w równoległoboku. Skorzystamy ze wzoru $P = a \cdot b \cdot \sin α$ , co daje $12 \sqrt{3} = 4 \cdot 6 \cdot \sin α$ . Wynika stąd, że $\sin α = \frac{\sqrt{3}}{2}$ , więc $α = 60 °$ . Kąt rozwarty oznaczymy jako $β$ . Zatem $β = \frac{360 ° - 120 °}{2} = 120 °$ .

Korzystając z rysunku oraz twierdzenia cosinusówtwierdzenie cosinusówtwierdzenia cosinusów wyznaczymy długości przekątnych.

RNNCrbkavvpVa

Ilustracja przedstawia równoległobok ABCD. Zaznaczono kąty wewnętrzne, przy wierzchołku a kąt alfa, przy wierzchołku D kąt beta.

Zatem

${|B D|}^{2} = {|A B|}^{2} + {|A D|}^{2} - 2 \cdot |A B| \cdot |A D| \cdot \cos 60 ° = 36 + 16 - 48 \cdot \frac{1}{2} = 28$ ,

czyli $|B D| = 2 \sqrt{7}$ oraz

${|A C|}^{2} = {|A B|}^{2} + {|B C|}^{2} - 2 \cdot |A B| \cdot |B C| \cdot \cos 120 ° =$

$= 36 + 16 - 48 \cdot \cos (180 ° - 60 °) =$

$= 52 + 48 \cdot \cos 60 ° = 52 + 24 = 76$ ,

czyli $|A C| = 2 \sqrt{19}$ .

Przykład 4

Dane są dwa równoległoboki $K L M N$ i $A B C D$ , których odpowiednie przekątne są tej samej długości: $|A C| = |K M| = d_{1}$ oraz $|B D| = |L N| = d_{2}$ .

R1EuBwYSpwcCA

Ilustracja przedstawia równoległoboki KLMN i ABCD, których przekątne AC i KM są równe długości d indeks dolny 1 koniec indeksu oraz przekątne BD i LN są równe długości d indeks dolny 2 koniec indeksu. Kąt między przekątnymi w równoległoboku ABCD ma miarę gamma, a w równoległoboku KLMN ma miarę alfa.

Wyznaczymy stosunek pól tych równoległoboków.

Rozwiązanie

Skorzystamy ze wzoru wykorzystującego długości przekątnych oraz miarę kąta pomiędzy nimi w równoległoboku.

$P_{K L M N} = \frac{d_{1} \cdot d_{2}}{2} \sin α$ , $P_{A B C D} = \frac{d_{1} \cdot d_{2}}{2} \sin γ$ .

Wtedy $\frac{P_{K L M N}}{P_{A B C D}} = \frac{\sin α}{\sin γ}$ .

Przykład 5

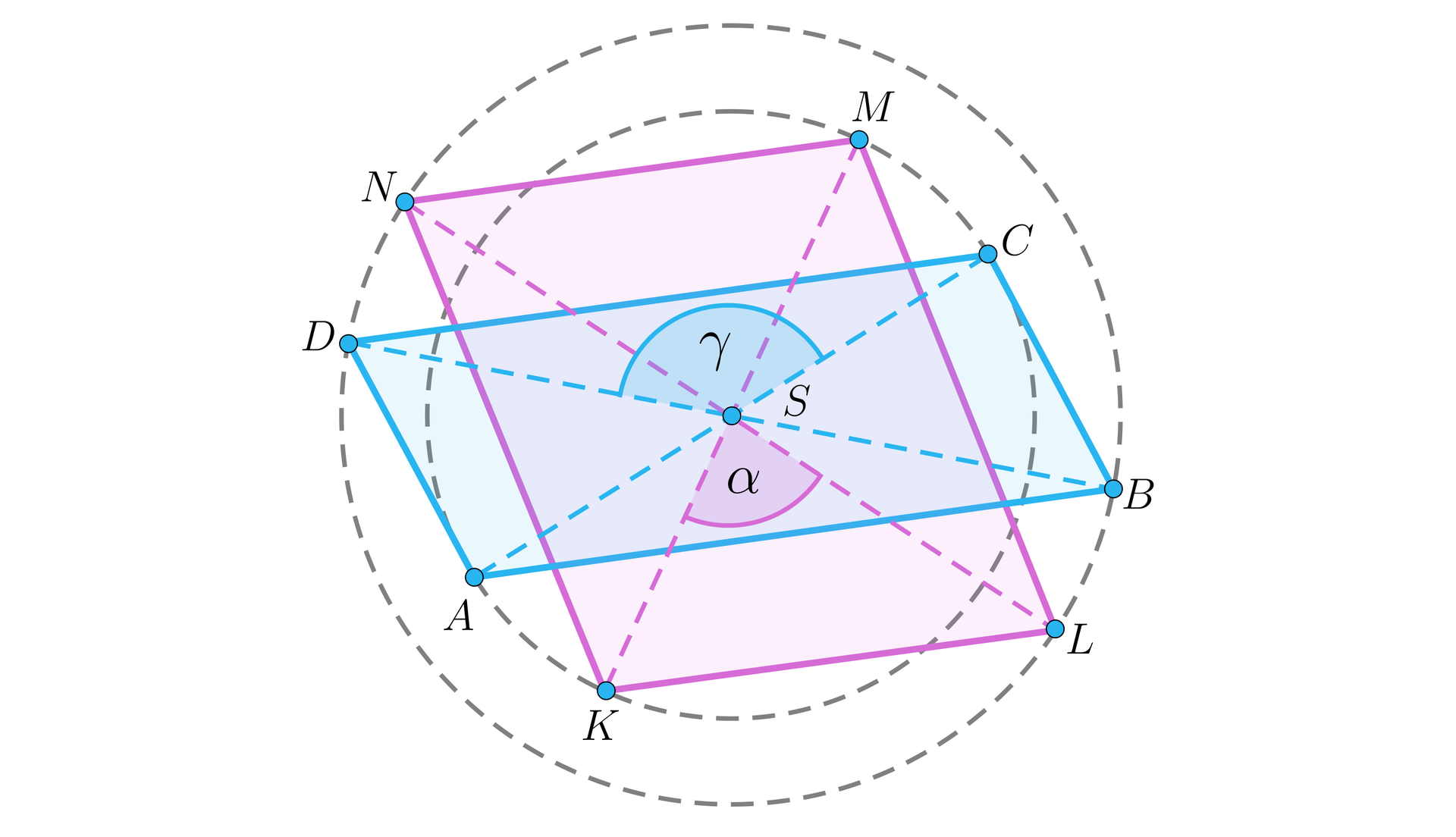
Na rysunku przedstawiony jest kwadratkwadratkwadrat oraz prostokątprostokątprostokąt, którego przekątne mają tę samą długość $d$ . Wpisujemy je w okrąg o promieniu $\frac{d}{2}$ .

R19282bCR2Qwf

Ilustracja przedstawia dwa czworokąty wpisane w okrąg. Prostokąt ABCD i kwadrat AGCH. Ich przekątne przecinają się w punkcie O będącym środkiem okręgu.

Pokażemy, że pola kwadratukwadratkwadratu $A H C G$ i prostokąta $A B C D$ są różne.

Rozwiązanie

Rzeczywiście, pole kwadratu $A H C G$ jest równe

$2 \cdot P_{C A G} = 2 \cdot \frac{\frac{d}{2} \cdot d}{2} = \frac{d^{2}}{2}$ .

Natomiast, pole prostokąta $A B C D$ jest równe $2 \cdot P_{C A D} = 2 \cdot \frac{h d}{2} = h d$ , gdzie $h$ jest wysokością trójkąta $C A D$ .

Długością wysokości $h$ jest odległość punktu $D$ od średnicy $A C$ okręgu. Z własności okręgu odległość ta jest mniejsza od promienia, czyli $h < \frac{d}{2}$ i stąd $h d < \frac{d^{2}}{2}$ .

o polu prostokąta

Twierdzenie: o polu prostokąta

Pole prostokąta o przekątnej $d$ i kącie $γ$ między przekątnymi jest równe $P = \frac{d^{2}}{2} \sin γ$ .

Dowód

Korzystamy ze wzoru na pole równoległoboku wstawiając w miejsce $d_{1}$ i $d_{2}$ wartość $d$ .

Przykład 6

Pokażemy, że pole kwadratu o przekątnej $d$ jest równe $\frac{d^{2}}{2}$ .

Rozwiązanie

W kwadracie przekątne przecinają się pod kątem prostym, więc $\sin γ = 1$ . Podstawiając tę wartość do wzoru na pole prostokąta dostajemy, że pole kwadratu jest równe $\frac{d^{2}}{2}$ .

o polu deltoidu

Twierdzenie: o polu deltoidu

Pole deltoidu o przekątnych $d_{1}$ , $d_{2}$ jest równe $P = \frac{d_{1} \cdot d_{2}}{2}$ .

Dowód

Aby wyznaczyć pole deltoidu, oznaczmy go $A B C D$ , skorzystamy z umiejętności obliczania pól trójkątów prostokątnych. Oznaczmy przez $S$ punkt przecięcia przekątnych tego deltoidu. Pole deltoidu jest sumą trójkątów $A B C$ i $A D C$ , więc pole deltoidu jest sumą pól tych trójkątów.

$P_{A B C D} = P_{A B C} + P_{A D C} = \frac{|B S| \cdot |A C|}{2} + \frac{|D S| \cdot |A C|}{2} = \frac{|A C|}{2} (|B S| + |D S|) = \frac{d_{1} \cdot d_{2}}{2}$

Zauważmy, że rombrombromb i kwadrat są deltoidami, więc do obliczenia ich pól możemy zastosować bezpośrednio twierdzenie o polu deltoidudeltoiddeltoidu.

Przykład 7

Pokażemy, że dla deltoidu o przekątnych $d_{1}$ , $d_{2}$ zachodzi nierówność $P \leq \frac{1}{4} ({d_{1}}^{2} + {d_{2}}^{2})$ , gdzie $P$ – pole deltoidu.

Rozwiązanie

Skorzystamy ze wzoru na pole deltoidu $P = \frac{d_{1} \cdot d_{2}}{2}$ . Wówczas:

$\frac{d_{1} \cdot d_{2}}{2} \leq \frac{1}{4} ({d_{1}}^{2} + {d_{2}}^{2})$ ,

$0 \leq \frac{1}{4} {d_{1}}^{2} - \frac{1}{2} d_{1} \cdot d_{2} + \frac{1}{4} {d_{2}}^{2}$ ,

$0 \leq {(\frac{1}{2} {d_{1}}^{} - \frac{1}{2} {d_{2}}^{})}^{2}$ .

Ostatnia nierówność jest spełniona zawsze, więc teza została udowodniona.

Zestawienie wzorów stosowanych do obliczania pól czworokątów z wykorzystaniem przekątnych.

Czworokąt	Wzór na pole z wykorzystaniem przekątnych
Trapez	brak
Równoległobok	$\frac{d_{1} \cdot d_{2}}{2} \sin γ$
Prostokąt	$\frac{d^{2}}{2} \sin γ$
Deltoid	$\frac{d_{1} \cdot d_{2}}{2}$
Romb	$\frac{d_{1} \cdot d_{2}}{2}$
Kwadrat	$\frac{d^{2}}{2}$

Słownik

czworokąt wypukły

czworokąt, którego wszystkie cztery kąty wewnętrzne są wypukłe

trapez

czworokąt, który ma przynajmniej jedną parę boków równoległych

trapez równoramienny

trapez, którego ramiona mają równe długości

równoległobok

czworokąt, który ma dwie pary boków równoległych

prostokąt

czworokąt, który ma wszystkie kąty proste

kwadrat

czworokąt, który ma wszystkie boki równe i wszystkie kąty proste

romb

czworokąt, który ma wszystkie boki równe

deltoid

czworokąt wypukłyczworokąt wypukłyczworokąt wypukły, który ma dwie pary równych boków sąsiednich

twierdzenie cosinusów

w dowolnym trójkącie kwadrat długości boku jest równy sumie kwadratów długości dwóch pozostałych boków tego trójkąta pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta między tymi bokami

Wprowadzenie

Symulacja interaktywna

Słownik