Punkt $E$ jest środkiem boku $BC$ równoległoboku $ABCD$. Prosta $AE$ przecina w punkcie $F$ prostą $CD$. Punkt $G$ jest takim punktem boku $CD$, że odcinek $EG$ jest prostopadły do prostej $AE$, jak na rysunku.

R1b1Qu3w7Yyyl

Na ilustracji przedstawiono równoległobok $ABCD$. Zaznaczono punkt E, stanowiący środek boku $CB$. Linią przerywaną zaznaczono prostą, na której leży bok $DC$, oraz prostą przechodzącą przez wierzchołek A i punkt E. Obie proste przecinają się w punkcie F. Linią przerywaną zaznaczono także prostą prostopadłą do prostej $AF$, przechodzącą przez punkt E i przecinającą bok $DC$ w punkcie G.

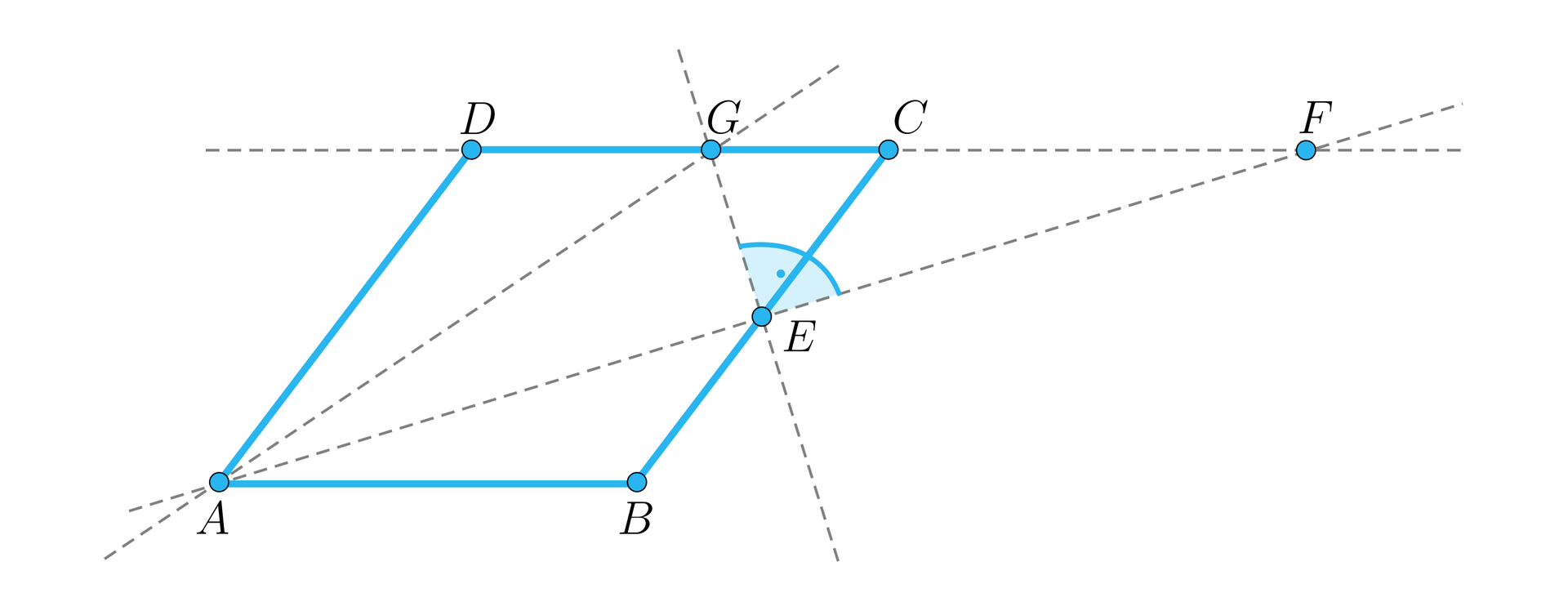
Wykażemy, że trójkąty $AEG$ i $FEG$ są przystające.

Oczywiście trójkąty $AEG$ i $FEG$ są prostokątne. Skorzystamy z cechy, która orzeka, że jeżeli dwie przyprostokątne jednego trójkąta są odpowiednio równe dwóm przyprostokątnym drugiego trójkąta, to trójkąty te są przystające. Odcinek $EG$ jest wspólną przyprostokątną w obu trójkątach.

Pozostaje wykazać, że $\left|AE\right|=\left|FE\right|$. W tym celu skorzystamy z faktu, że trójkąty $ABE$ i $FCE$ są przystające. Istotnie:

• kąty $AEB$ i $FEC$ jako wierzchołkowe są równe;

• kąty $BAE$ i $CFE$ jako naprzemianległe są równe.

Stąd wynika równość kątów $FCE$ i $ABE$. Ale to oznacza, że kąty przyległe do boku $BE$ w trójkącie $ABE$ i boku $CE$ w trójkącie $FCE$ są odpowiednio równe. Ale boki $BE$ i $CE$, równe połowie boku $BC$, są sobie równe. Zatem na mocy cechy kbk trójkąty $ABE$ i $FCE$ są przystające. Co pozwala stwierdzić, że odcinki $AE$ i $FE$ mają równą długość. Co należało wykazać.

Zauważmy, że z powyższego twierdzenia wynika w szczególności, że prosta $AF$ jest dwusieczną kąta $BAG$.

Dany jest trójkąt równoramienny $ABC$, w którym $\left|AC\right|=\left|BC\right|$. Na bokach tego trójkąta zbudowano trzy trójkąty równoboczne: $ABD$, $BCE$, $ACF$, jak na rysunku.

R1TXaYEAVFUzX

Na ilustracji przedstawiono trójkąt równoramienny $ABC$ o podstawie $AB$. Na bokach trójkąta zbudowano trójkąty równoboczne $ACF$, $CBE$, $ABD$. Linią przerywaną zaznaczono trójkąt o wierzchołkach $DEF$.

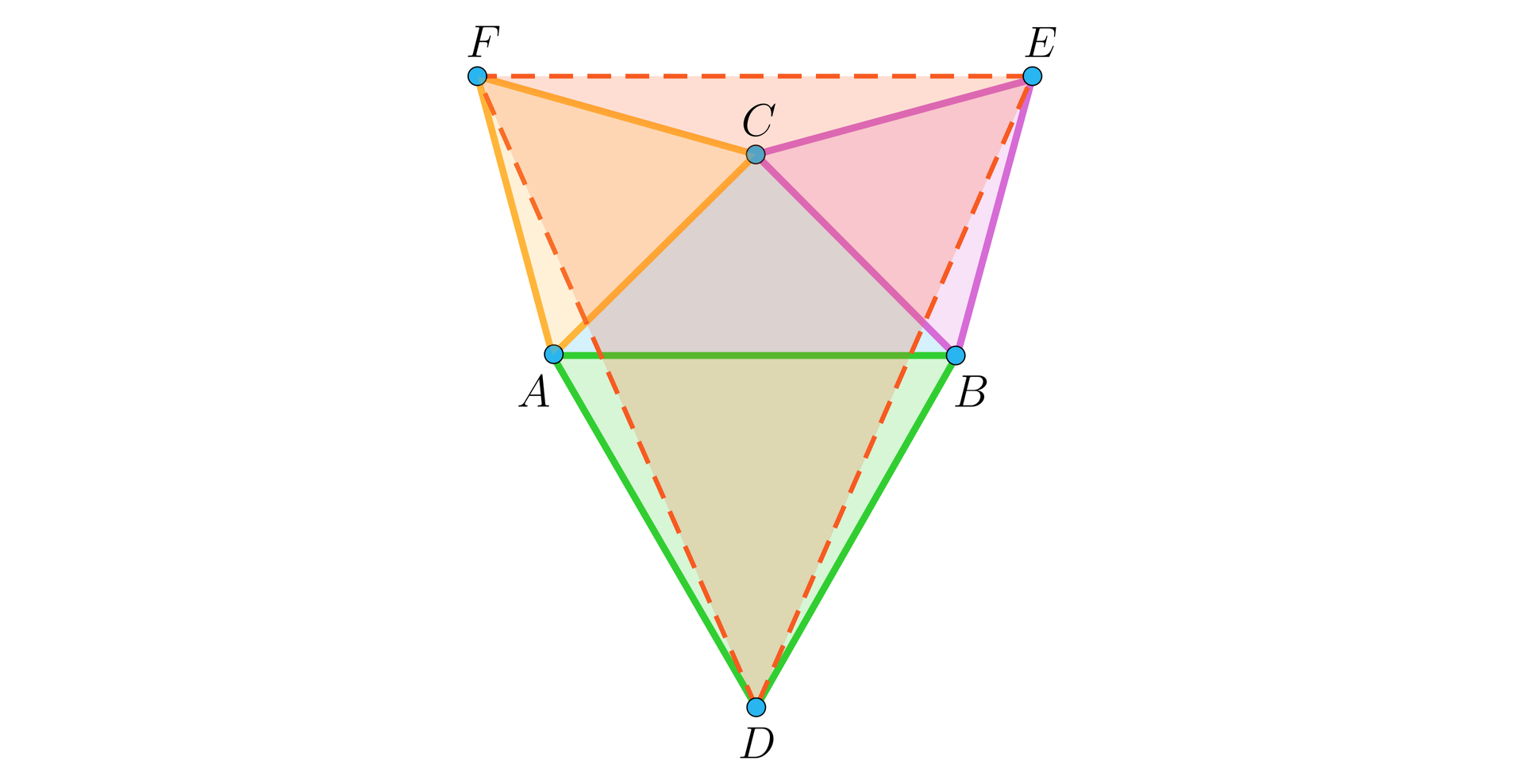
Pokażemy, że trójkąt $EDF$ jest równoramienny.

Dowód sprowadza się do wykazania, że $△DBE\equiv △DAF$, czyli, że trójkąty te są przystające.

Przyjmijmy oznaczenie $\left|\sphericalangle BAC\right|=\left|\sphericalangle ABC\right|=\alpha$.

Zauważmy, że $\left|BE\right|=\left|BC\right|$ oraz $\left|AF\right|=\left|AC\right|$, co wynika z faktu, że dobudowane trójkąty są równoboczne. Ale $\left|AC\right|=\left|BC\right|$, zatem $\left|BE\right|=\left|AF\right|$.

Zauważmy dalej, że $\left|AD\right|=\left|BD\right|$ oraz $\left|\sphericalangle DAF\right|=60°+\alpha +60°=120°+\alpha$. Ale $\left|\sphericalangle DBE\right|=60°+\alpha +60°=120°+\alpha$.

Zatem w trójkątach $DBE$ i $DAF$ dwa boki i kąt leżący między tymi bokami są odpowiednio równe, czyli na mocy cechy bkb te trójkąty są przystające. W szczególności boki leżące naprzeciw kątów $DBE$ i $DAF$ są równe.

Stąd $\left|ED\right|=\left|FD\right|$, co należało wykazać.

Rozważymy teraz związki miarowe, gdy trójkąty równoboczne zbudujemy na bokach dowolnego trójkąta. Dany jest trójkąt $ABC$. Na bokach tego trójkąta zbudowano trzy trójkąty równoboczne: $ABD$, $BCE$, $ACF$, jak na rysunku.

RjgEEbuZqoG2S

Na ilustracji przedstawiono trójkąt różnoboczny $ABC$. Na bokach trójkąta zbudowani trójkąty równoboczne $ACF$, $ABD$, $BCE$. Linią przerywaną poprowadzono proste łączące wierzchołki trójkąta $ABC$, z przeciwległymi wierzchołkami dorysowanych trójkątów równobocznych, czyli wierzchołek A z wierzchołkiem E, wierzchołek B z wierzchołkiem F, wierzchołek C z wierzchołkiem D.

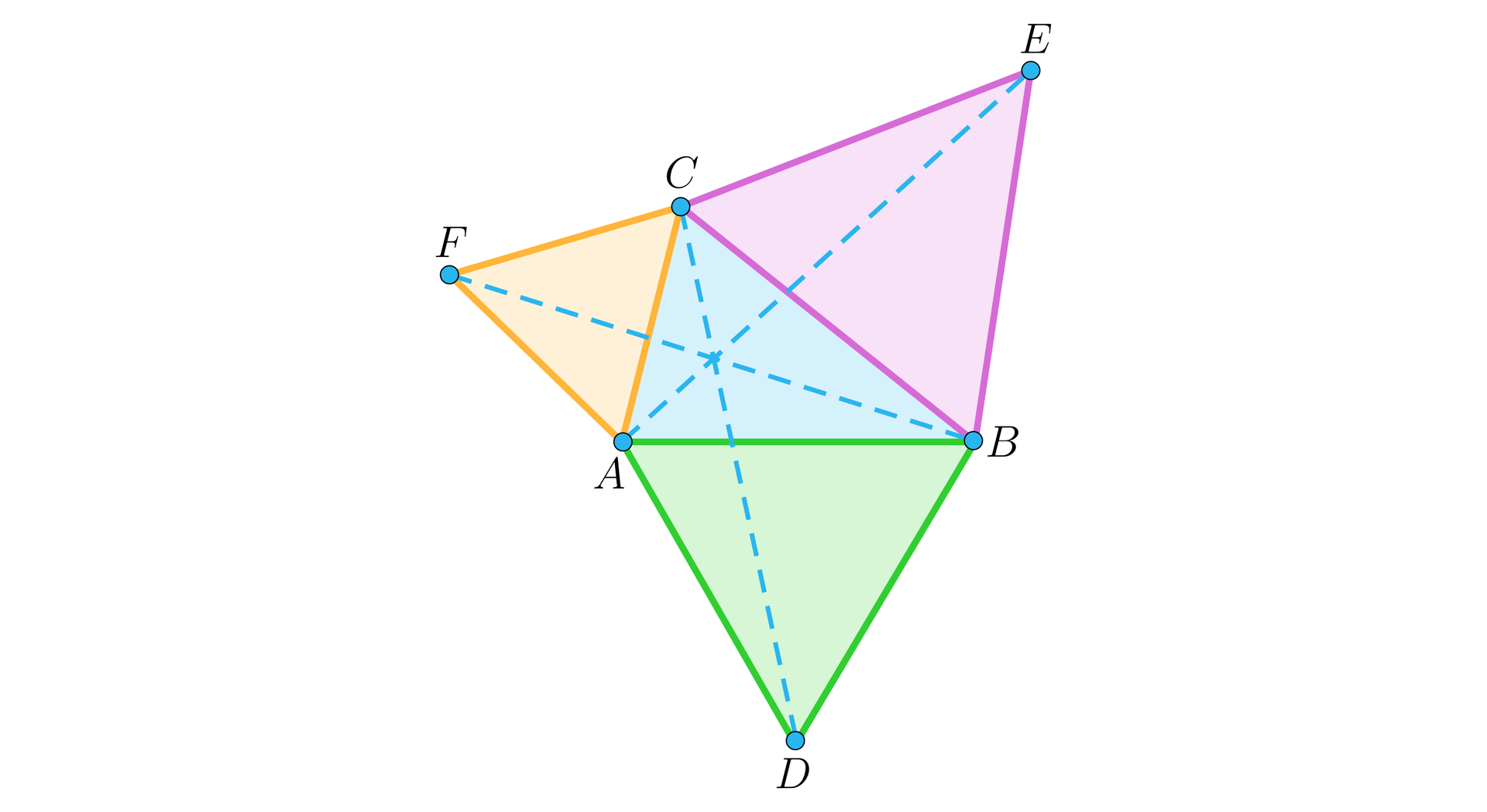
Pokażemy, że $\left|AE\right|=\left|BF\right|=\left|CD\right|$.

Pokażemy najpierw, że $△ACE\equiv △FCB$. Przyjmijmy oznaczenie $\left|\sphericalangle ACB\right|=\gamma$. Wtedy $\left|\sphericalangle FCB\right|=60°+\gamma$. Podobnie $\left|\sphericalangle ACE\right|=\gamma +60°$, zatem te kąty są równe. Pozostaje zauważyć, że boki $FC$ i $BC$ w trójkącie $FCB$ są odpowiednio równe bokom $AC$ i $CE$ w trójkącie $ACE$. Zatem na mocy cechy bkb te trójkąty są przystające. W szczególności boki $AE$ i $BF$ są równe.

Pokażemy teraz, że $△ABE\equiv △DBC$. Przyjmijmy oznaczenie $\left|\sphericalangle ABC\right|=\beta$. Wtedy $\left|\sphericalangle ABE\right|=\beta +60°$. Podobnie $\left|\sphericalangle DBC\right|=60°+\beta$, zatem te kąty są równe. Pozostaje zauważyć, że boki $AB$ i $BE$ w trójkącie $ABE$ są odpowiednio równe bokom $BD$ i $BC$ w trójkącie $DBC$. Zatem na mocy cechy bkb te trójkąty są przystające. W szczególności boki $AE$ i $CD$ są równe. Co należało wykazać.

Na bokach $AB$ i $BC$ kwadratu $ABCD$ obrano takie punkty $E$ i $F$, że $\left|EB\right|=\left|CF\right|$. Proste $AF$ i $CE$ przecinają się w punkcie $G$, jak na rysunku.

RVugN4sl8ZmcF

Na ilustracji przedstawiono kwadrat $ABCD$. Zaznaczono punkt F na boku $BC$, oraz punkt E na boku $EB$. Odcinki $EB$ oraz $CF$ są sobie równe. Linią przerywaną zaznaczono proste przechodzące przez wierzchołek A i punkt F, oraz wierzchołek C i punkt E. Proste przecinają się w punkcie G. $\angle FDE$jest równy alfa. Łukiem zaznaczono $\angle CGA$.

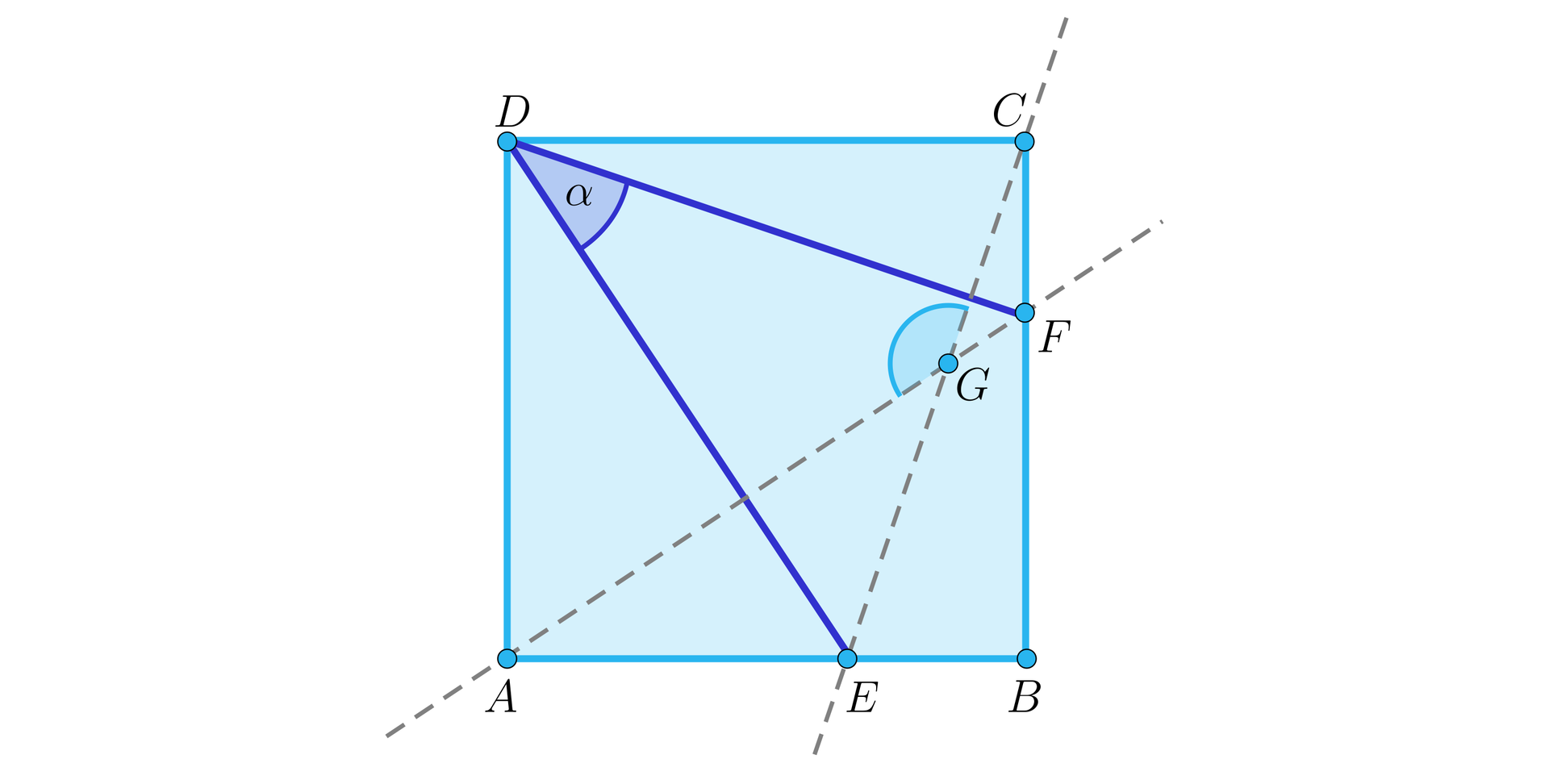
Miara kąta $EDF$ jest równa $\alpha$. Wykażemy, że miara kąta $AGC$ jest równa $180°-\alpha$.

Przyjmiemy oznaczenia: $\left|\sphericalangle BAF\right|=\beta$, $\left|\sphericalangle BCE\right|=\gamma$. Wtedy $\left|\sphericalangle AGC\right|=360°-\left|\sphericalangle DAF\right|-\left|\sphericalangle ADC\right|-\left|\sphericalangle DCE\right|$, czyli $\left|\sphericalangle AGC\right|={360}^{\circ }-({90}^{\circ }-\beta )-({90}^{\circ }-\gamma )-{90}^{\circ }={90}^{\circ }+\beta +\gamma$.

Ale trójkąty $EBC$ i $FCD$ są przystające, w szczególności $\left|\sphericalangle CDF\right|=\left|\sphericalangle BCE\right|=\gamma$. Podobnie trójkąty $AED$ i $BFA$ są przystające, w szczególności $\left|\sphericalangle ADE\right|=\left|\sphericalangle BAF\right|=\beta$. Ale $\left|\sphericalangle ADE\right|+\alpha +\left|\sphericalangle CDF\right|=90°$, stąd $\left|\sphericalangle ADE\right|+\left|\sphericalangle CDF\right|=\beta +\gamma =90°-\alpha$.

Zatem $\left|\sphericalangle AGC\right|=90°+\beta +\gamma =90°+\left(90°-\alpha \right)=180°-\alpha$. Co należało wykazać.

zestaw twierdzeń określających warunki równoważne występowania relacji przystawania między dwoma trójkątami