Układem równań nazywamy koniunkcję co najmniej dwóch równań.

Znajdźmy rozwiązania układu równań

$\left\{\begin{array}{l}{z}^2+x+y=12\\ x-y=-2\\ x^2=9\end{array}\right.$.

Z trzeciego równania możemy obliczyć $x=-3$ lub $x=3$.

Drugie równanie przekształcamy równoważnie tak, aby wyznaczyć z niego $y$.

$x-y=-2$

$y=x+2$

A wtedy $y=-3+2=-1$ lub $y=3+2=5$.

Teraz przekształcamy trzecie równanie i wyznaczamy z niego wartość zmiennej $z$.

$z^2+x+y=12$

$z^2=12-\left(x+y\right)$

Stąd:

$z^2=12-\left(-3-1\right)=12+4=16\Rightarrow z=-4$ lub $z=4$

lub

$z^2=12-\left(3+5\right)=12-8=4\Rightarrow z=-2$ lub $z=2$.

A zatem otrzymaliśmy cztery trójki liczb, które są rozwiązaniami tego układu równań:

$\left\{\begin{array}{l}x=-3\\ y=-1\\ z=-4\end{array}\right.$ lub $\left\{\begin{array}{l}x=-3\\ y=-1\\ z=4\end{array}\right.$ lub $\left\{\begin{array}{l}x=3\\ y=5\\ z=-2\end{array}\right.$ lub $\left\{\begin{array}{l}x=3\\ y=5\\ z=2\end{array}\right.$.

Co możemy też zapisać w postaci: $\left(-3, -1, 4\right)$, $\left(-3, -1, -4\right)$, $\left(3, 5, -2\right)$, $\left(3, 5, 2\right)$.

Rozwiązaniem układu równań nazywamy odpowiednio parę, trójkę, czwórkę itd. liczb spełniających każde z równań składowych danego układu równań.

Sprawdzimy, które z czwórek liczb  $\left(3, -2, 2, -1\right)$, $\left(-3, 2, -2, -1\right)$, $\left(3, -2, 2, 1\right)$ spełniają układ równańukład równańukład równań

$\left\{\begin{array}{l}x+y+z+t^2=4\\ t^2+x=z-y\\ t^2=1\\ x+z=y+7\end{array}\right.$

Rozpatrzmy czwórkę liczb  $\left(3, -2, 2, -1\right)$, czyli

$\left\{\begin{array}{l}x=3\\ y=-2\\ z=2\\ t=-1\end{array}\right.$.

Sprawdzamy wartości liczbowe wyrażeń znajdujących się po lewej stronie kolejnych równań składowych i porównujemy je z wartościami liczbowymi znajdującymi się po prawej stronie tych równań.

$L_1=x+y+z+t^2=3+\left(-2\right)+2+{\left(-1\right)}^2=4=P_1\Rightarrow L_1=P_1$

$L_2=t^2+x={\left(-1\right)}^2+3=4$

$P_2=z-y=2-\left(-2\right)=4\Rightarrow L_2=P_2$

$L_3=t^2={\left(-1\right)}^2=1$

$P_3=1\Rightarrow L_3=P_3$

$L_4=x+z=3+2=5$

$P_4=y+7=-2+7=5\Rightarrow L_4=P_4$

A zatem układ liczb $\left(3, -2, 2, -1\right)$ jest rozwiązaniem układu

$\left\{\begin{array}{l}x+y+z+t^2=4\\ t^2+x=z-y\\ t^2=1\\ x+z=y+7\end{array}\right.$.

Sprawdzimy teraz czwórkę $\left(-3, 2, -2, -1\right)$, czyli

$\left\{\begin{array}{l}x=-3\\ y=2\\ z=-2\\ t=-1\end{array}\right.$.

Sprawdzamy wartości liczbowe wyrażeń znajdujących się po lewej stronie kolejnych równań składowych i porównujemy je z wartościami liczbowymi znajdującymi się po prawej stronie tych równań.

$L_1=x+y+z+t^2=-3+2+\left(-2\right)+{\left(-1\right)}^2=-2\ne 4=P_1\Rightarrow L_1\ne P_1$

A zatem układ liczb $\left(-3, 2, -2, -1\right)$ nie spełnia pierwszego równania. W tej sytuacji nie musimy już sprawdzać pozostałych równań – czwórka liczb $\left(-3, 2, -2, -1\right)$ nie jest rozwiązaniem układu

$\left\{\begin{array}{l}x+y+z+t^2=4\\ t^2+x=z-y\\ t^2=1\\ x+z=y+7\end{array}\right.$.

Przejdziemy teraz do sprawdzenia, czy czwórka $\left(3, -2, 2, 1\right)$ jest rozwiązaniem układu równań. Wiemy, że

$\left\{\begin{array}{l}x=3\\ y=-2\\ z=2\\ t=1\end{array}\right.$.

Sprawdzamy wartości liczbowe wyrażeń znajdujących się po lewej stronie kolejnych równań składowych i porównujemy je z wartościami liczbowymi znajdującymi się po prawej stronie tych równań.

$L_1=x+y+z+t^2=3+\left(-2\right)+2+1^2=4=P_1\Rightarrow L_1=P_1$

$L_2=t^2+x=1^2+3=4$

$P_2=z-y=2-\left(-2\right)=4\Rightarrow L_2=P_2$

$L_3=t^2=1^2=1$

$P_3=1\Rightarrow L_3=P_3$

$L_4=x+z=3+2=5$

$P_4=y+7=-2+7=5\Rightarrow L_4=P_4$

A zatem układ liczb $\left(3, -2, 2, 1\right)$ jest rozwiązaniem układu

$\left\{\begin{array}{l}x+y+z+t^2=4\\ t^2+x=z-y\\ t^2=1\\ x+z=y+7\end{array}\right.$.

Nie każdy układ równań posiada rozwiązanie.

Spróbujmy znaleźć rozwiązanie układu równańrozwiązanie układu równańrozwiązanie układu równań $\left\{\begin{array}{l}x+y=5\\ 2x-y=4\\ x-2y=2\end{array}\right.$.

Łatwo odgadnąć, że wspólnym rozwiązaniem dwóch pierwszych równań jest para liczb $\left(3, 2\right)$.

Jest to jedyne rozwiązanie układu tych równań.

Para ta nie spełnia jednak trzeciego równania składowego wyjściowego układu równań, a zatem nie jest jego rozwiązaniem.

Nie istnieje więc para, która spełnia jedocześnie wszystkie trzy równania składowe.

Układ ten nie ma zatem rozwiązania.

Taki układ równań nazywamy układem sprzecznymsprzeczny układ równańukładem sprzecznym.

Znajdźmy rozwiązania układu równań $\left\{\begin{array}{l}{x}^2+3y-2=0\\ 3x^2+9y=6\end{array}\right.$.

Widzimy, że drugie równanie powstaje z pierwszego, przez pomnożenie obu stron równania przez $3$.

Możemy też wyznaczyć $y$ z pierwszego i drugiego równania.

$x^2+3y-2=0$ i  $3x^2+9y=6$

$3y=2-x^2 \left|:3\right.$ i  $9y=6-3x^2 \left|:3\right.$

$y=\frac{2-x^2}{3}$ i  $3y=2-x^2 \left|:3\right.$

$y=\frac{2-x^2}{3}$ i  $y=\frac{2-x^2}{3}$

Otrzymaliśmy to samo wyrażenie, więc równania składowerównanie składowerównania składowe układu równań są równoważne.

Równanie $y=\frac{2-x^2}{3}$ ma nieskończenie wiele rozwiązań.

Zatem układ równań $\left\{\begin{array}{l}{x}^2+3y-2=0\\ 3x^2+9y=6\end{array}\right.$ również ma nieskończenie wiele rozwiązań postaci

$(x,\frac{2-x^2}{3})$, $x\in \mathrm{ℝ}$.

Taki układ równań nazywamy układem nieoznaczonymnieoznaczony układ równańukładem nieoznaczonym.

Liczbę rozwiązań układu równań można łatwo określić, analizując interpretacje geometryczne poszczególnych równań wchodzących w skład tego układu równań.

Korzystamy tu z naszej wiedzy dotyczącej wykresów różnych równań lub na podstawie wzoru tworzymy tabelkę, a następnie odpowiedni wykres.

Znajdźmy interpretację geometryczną układu równań i na tej podstawie określmy liczbę jego rozwiązań.

a) $\left\{\begin{array}{l}y=x\\ y=x^2\end{array}\right.$

RUlzZNZ5RtYrm

Grafika przedstawia układ współrzędnych z poziomą osią x od minus pięciu do sześciu i pionową osią y od minus czterech do pięciu. Na płaszczyźnie znajdują się dwa wykresy. Pierwszy wykres to prosta o równaniu $y=x$, drugi wykres to parabola o równaniu $y=x^2$. Wykresy przecinają się w dwóch punktach, które zostały zaznaczone zamalowanymi kropkami. Współrzędne pierwszego punktu to: początek nawiasu, 0, 0, zamknięcie nawiasu, współrzędne drugiego punktu to: początek nawiasu, 1, 1, zamknięcie nawiasu.

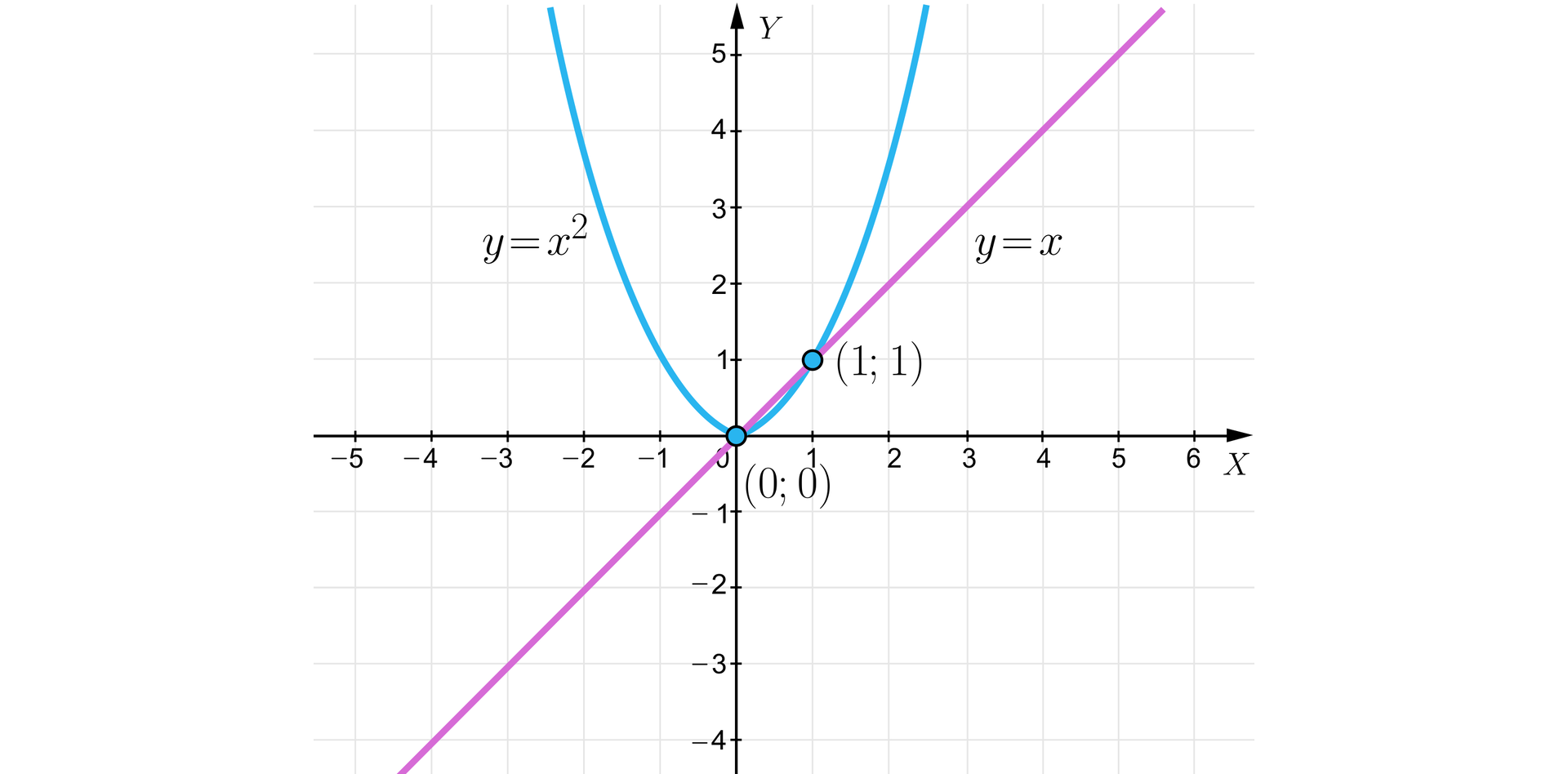
Narysowane wykresy mają dwa punkty wspólne, a zatem układ równańukład równańukład równań ma dwa rozwiązania.

Z wykresu możemy odczytać współrzędne tych punktów – $\left(0, 0\right)$ oraz $\left(1, 1\right)$.

Podstawiając do równań składowych pary liczb $\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$ oraz $\left\{\begin{array}{l}x=1\\ y=1\end{array}\right.$ możemy sprawdzić, czy dokładnie odczytaliśmy rozwiązanie.

b) $\left\{\begin{array}{l}y=x\\ y=x^2\\ y=\frac{1}{x}\end{array}\right.$

RviTtDxJlgNx5

Grafika przedstawia układ współrzędnych z poziomą osią x od minus sześciu do sześciu i pionową osią y od minus czterech do pięciu. Na płaszczyźnie znajdują się trzy wykresy. Pierwszy wykres to prosta o równaniu $y=x$, drugi wykres to parabola o równaniu $y=x^2$. Trzeci wykres ma kształt hiperboli o równaniu $y=\frac{1}{x}$. Wykresy przecinają się w dwóch punktach, które zostały zaznaczone zamalowanymi kropkami. Współrzędne pierwszego punktu to: początek nawiasu, 0, 0, zamknięcie nawiasu, współrzędne drugiego punktu to: początek nawiasu, 1, 1, zamknięcie nawiasu.

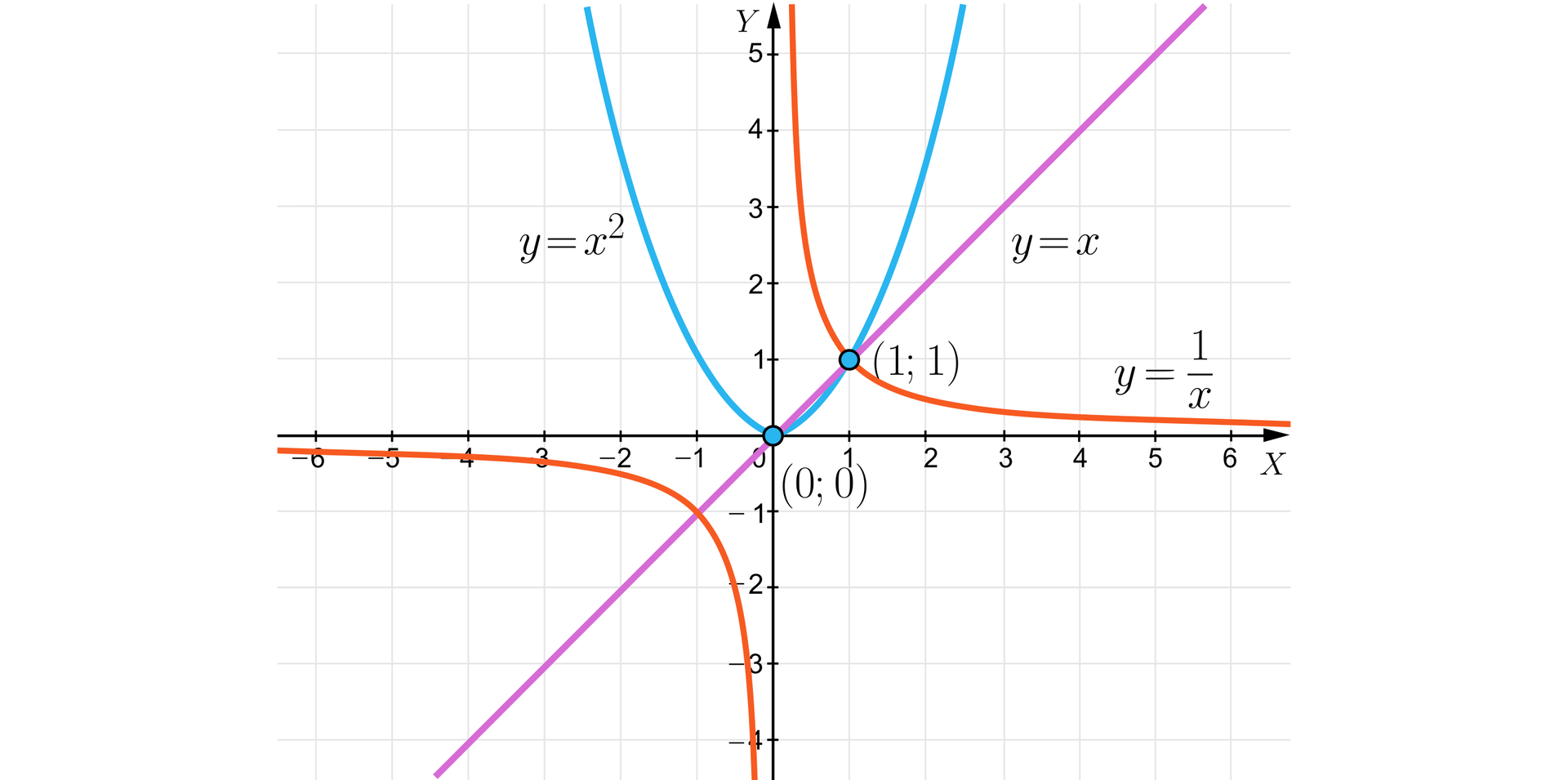
Istnieje tylko jeden punkt wspólny tych trzech wykresów, a więc układ równań ma dokładnie jedno rozwiązanie.

koniunkcja co najmniej dwóch równań

układ liczb spełniających każde z równań składowych w tym układzie

równanie wchodzące w skład układu równań

układ równań, który nie posiada rozwiązania

układ równań, który posiada nieskończenie wiele rozwiązań