Kwadrat ma pole $100$. Wierzchołki kwadratu połączono ze środkami przeciwległych boków. Wyznaczmy pole zacieniowanego kwadratu.

R1tA5ZVcHgLUW

Na ilustracji przedstawiono kwadrat $ABCD$. Wierzchołek A połączono z punktem G, stanowiącym środek boku $DC$. Wierzchołek B połączono z punktem H, stanowiącym środek boku $AD$. Wierzchołek C połączono z punktem E, stanowiącym środek boku $AB$. Wierzchołek D połączono z punktem F, stanowiącym środek boku $BC$. Odcinek $AG$, przecina odcinek $BH$ w punkcie J, oraz odcinek $DF$ w punkcie I. Odcinek $CE$ przecina odcinek $DF$ w punkcie L, oraz odcinek $BH$ w punkcie K. Powstał kwadrat $IJKL$.

Rozwiązanie

RolCiiJuG1uFh

Na ilustracji przedstawiono kwadrat $ABCD$. Wierzchołek A połączono z punktem G, stanowiącym środek boku $DC$. Wierzchołek B połączono z punktem H, stanowiącym środek boku $AD$. Wierzchołek C połączono z punktem E, stanowiącym środek boku $AB$. Wierzchołek D połączono z punktem F, stanowiącym środek boku $BC$. Odcinek $AG$, przecina odcinek $BH$ w punkcie J, oraz odcinek $DF$ w punkcie I. Odcinek $CE$ przecina odcinek $DF$ w punkcie L, oraz odcinek $BH$ w punkcie K. Powstał kwadrat $IJKL$. Zaznaczono punkt I prim, na przedłużeniu odcinka $GI$, taki że odcinek $GI\text{'}$ równa się odcinkowi $GI$. Zacieniowano różowym kolorem trójkąt $GID$, oraz trójkąt $GI\text{'}C$.

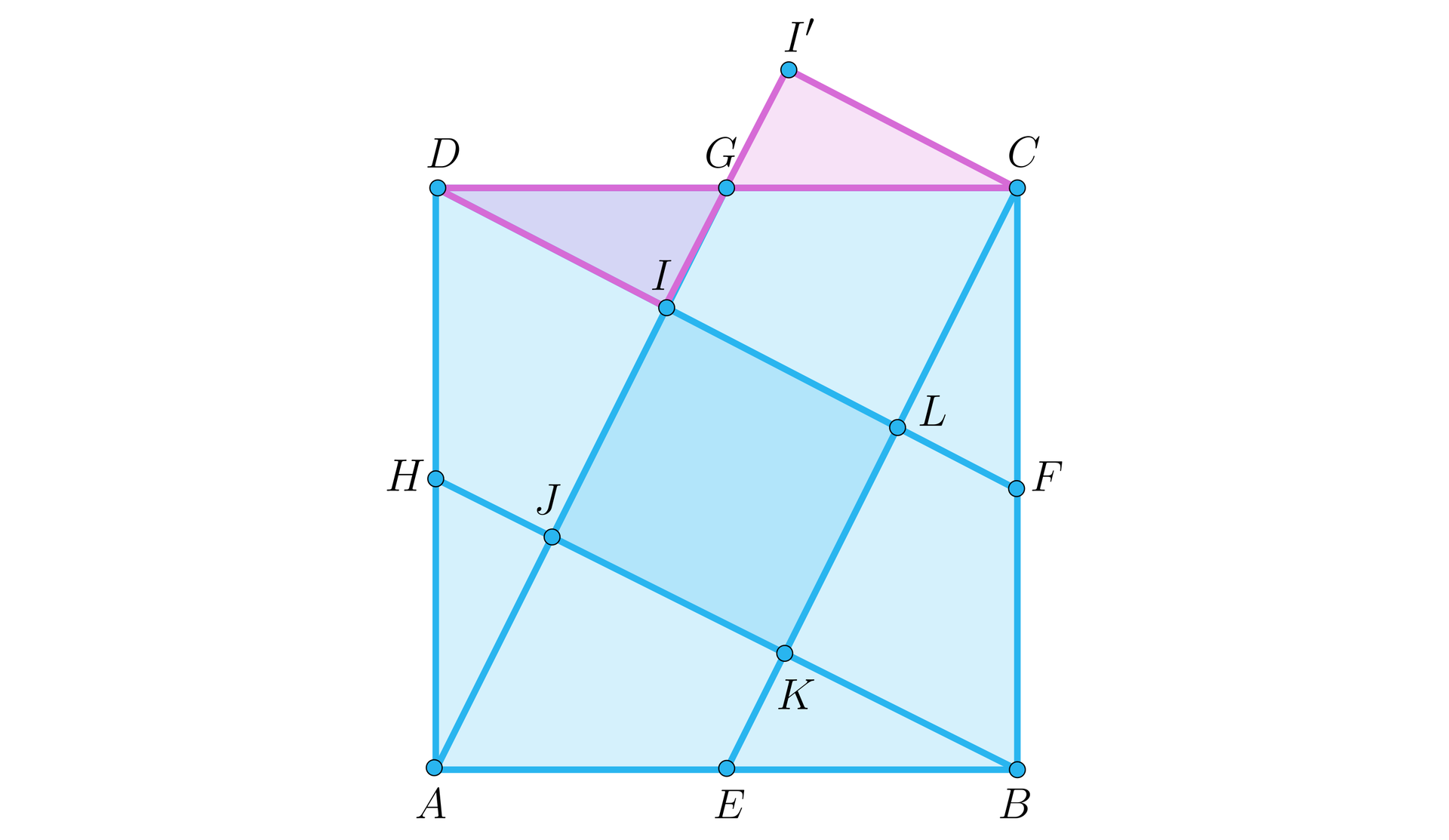
Zauważmy, że różowe trójkąty są przystające, więc kwadrat $ILCI\text{'}$ jest przystający do zacieniowanego. Podobnie możemy uzyskać pozostałe trzy inne przystające kwadraty. Duży kwadrat „składa się” z pięciu takich kwadratów. Więc szukane pole zacieniowanego kwadratu jest równe $20$.

Trójkąt $ABC$ ma pole równe  $1$. Punkt $A\text{'}$ leży na prostej $AB$, bliżej punktu $B$ oraz $AB=BA\text{'}$. Punkt $B\text{'}$ leży na prostej $BC$, bliżej punktu $C$ oraz $BC=CB\text{'}$. Punkt $C\text{'}$ leży na prostej $CA$, bliżej punktu $A$ oraz $CA=AC\text{'}$. Zastanówmy się jak obliczyć pole trójkąta $A\text{'}B\text{'}C\text{'}$.

R7EHZo61xuCmt

Na ilustracji przedstawiono trójkąt $ABC$. Na przedłużeniu boku $CA$ znajduje się punkt C prim. Na przedłużeniu boki $BC$ znajduje się punkt B prim. Na przedłużeniu boku $AB$ znajduje się punkt A prim. Punkty A prim, B prim, C prim po połączeniu utworzyły trójkąt.

Rozwiązanie

RvGtogeuLjPVJ

Na ilustracji przedstawiono trójkąt $ABC$. Na przedłużeniu boku $CA$ znajduje się punkt C prim. Na przedłużeniu boku $BC$ znajduje się punkt B prim. Na przedłużeniu boku $AB$ znajduje się punkt A prim. Punkty A prim, B prim, C prim po połączeniu utworzyły trójkąt. Linią przerywaną połączono wierzchołki A i C prim, B i A prim, C i B prim.

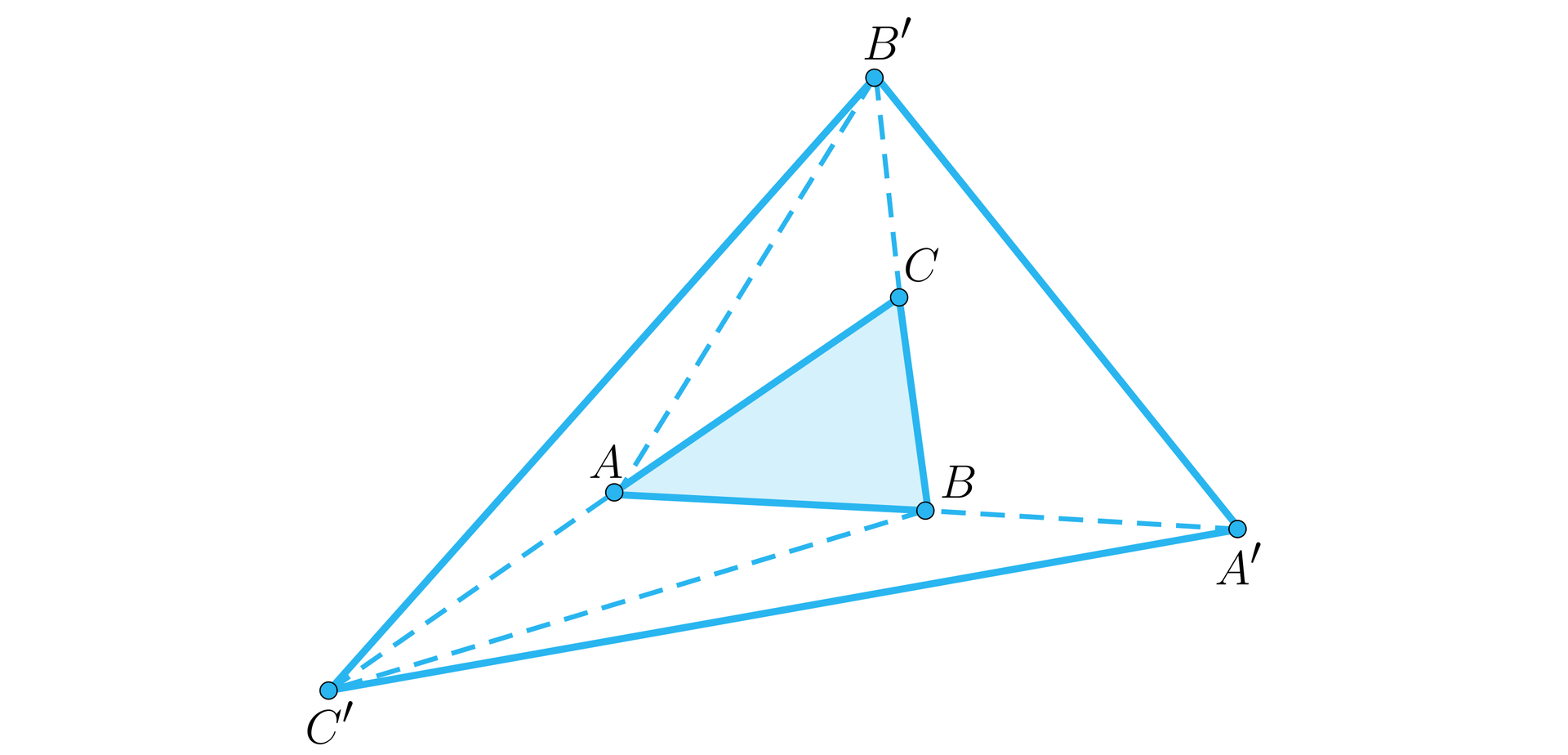
Wykorzystamy prosty fakt, że środkowa trójkąta dzieli go na dwa trójkąty o równych polach. Dowód tej własności wynika bezpośrednio z definicji środkowej i wzoru na pole trójkąta. Korzystając z powyższej obserwacji dla trójkątów $AA\text{'}C$, $BB\text{'}A$, $CC\text{'}B$ dostajemy równości pól:

$P_{ABC}=P_{A^{\prime }BC}$, $P_{ABC}=P_{A{B}^{\prime }C}$, $P_{ABC}=P_{AB{C}^{\prime }}$.

Podobnie dla trójkątów $AA\text{'}C\text{'}$, $BB\text{'}A\text{'}$, $CC\text{'}B\text{'}$ otrzymujemy równości:

$P_{CB{A}^{\prime }}=P_{C{B}^{\prime }{A}^{\prime }}$,  $P_{AC{B}^{\prime }}=P_{A{C}^{\prime }{B}^{\prime }}$, $P_{A{C}^{\prime }B}=P_{A^{\prime }{C}^{\prime }B}$.

Więc pole trójkąta $A\text{'}B\text{'}C\text{'}$ jest równe $7$.

Przekątne trapezu $ABCD$ o podstawach $AB$ i $CD$ przecinają się w punkcie $P$. Uzasadnijmy, że pole trójkąta $ADP$ jest równe polu trójkąta $BCP$.

Rozwiązanie

R1eVchs56X6Ak

Na ilustracji przedstawiono trapez $ABCD$, o podstawach $AB$ i $CD$. Zaznaczono przekątne $AC$, oraz $DB$, które przecinają się w punkcie P. Żółtym kolorem obrysowano trójkąt $APB$.

Zauważmy, że punkty $D$ i $C$ leżą na prostej  równoodległej  od prostej $AB$, więc trójkąty $ABD$ i $ABC$ mają taką samą podstawę i tę samą długość wysokości. Zatem mają równe pola $P_{ABD}=P_{ABC}$. Pola tych trójkątów są ponadto równe sumie pól trójkątów odpowiednio $ADPiABP$ oraz $BCPiABP$. Odejmując obustronnie od równości $P_{ADP}+P_{ABP}=P_{BCP}+P_{ABP}$ wartość pola trójkąta $ABP$ otrzymujemy tezę.

Uzasadnimy, że suma odległości dowolnego punktu   $P$ leżącego wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.

Rozwiązanie

R1aJjmDVtE3E6

Na ilustracji przedstawiono trójkąt równoboczny $ABC$. Zaznaczono punkt P wewnątrz trójkąta. Na boku A C zaznaczono punkt E taki, że odcinek E P jes prostopadły do tego boku, na boku A B zaznaczono punkt F taki, że odcinek P F jest prostopadły do tego boku oraz na boku B C zaznaczono punkt D taki, że odcinek P D jest prostopadły do tego boku. Linią przerywaną poprowadzono odcinki łączące punkt P z każdym wierzchołkiem trójkąta.

Oznaczmy długość boku trójkąta przez  $a$, wysokość przez  $h$ oraz końce odcinków wyznaczających odległość punktu $P$ od boków $BC$, $CA$, $AB$ odpowiednio $D$, $E$, $F$.

Policzmy pole trójkąta równobocznego $ABC$ na dwa sposoby:

$P=\frac{1}{2}a\cdot h$

oraz

$P=P_{ABP}+P_{BCP}+P_{CAP}=\frac{1}{2}a\cdot \left|PF\right|+\frac{1}{2}a\cdot \left|PD\right|+\frac{1}{2}a\cdot \left|PE\right|$.

Zatem otrzymujemy

$\frac{1}{2}a·\left(\left|PF\right|+\left|PD\right|+\left|PE\right|\right)=\frac{1}{2}a·h$.

Dzieląc obustronnie powyższą równość przez $\frac{1}{2}a$ otrzymujemy

$\left|PF\right|+\left|PD\right|+\left|PE\right|=h$.

Zatem suma odległości nie zależy od wyboru punktu $P$ i jest równa wysokości wyjściowego trójkąta równobocznego.

Punty $E$, $F$, $G$, $H$ są środkami odcinków odpowiednio  $AB$, $BC$, $CD$, $DA$ czworokąta $ABCD$. Niech proste $EG$ i $FH$ przecinają się w punkcie $P$. Udowodnimy, że suma pól czworokątów $AEPH$ i $PFCG$ jest równa sumie pól czworokątów $EBFP$ i $HPGP$.

RU1Qntts2E1QA

Na ilustracji przedstawiono czworokąt $ABCD$. Punkt E stanowi środek boku $AB$, punkt F stanowi środek boku $BC$, punkt G stanowi środek boku $DC$, oraz punkt H stanowi środek boku $AD$. Zaznaczono odcinki łączące punkty G i E, oraz H i F. W miejscu przecięcia się odcinków zaznaczono punkt P. Zacieniowano powstałe czworokąty $PGCF$, oraz $AHPE$.

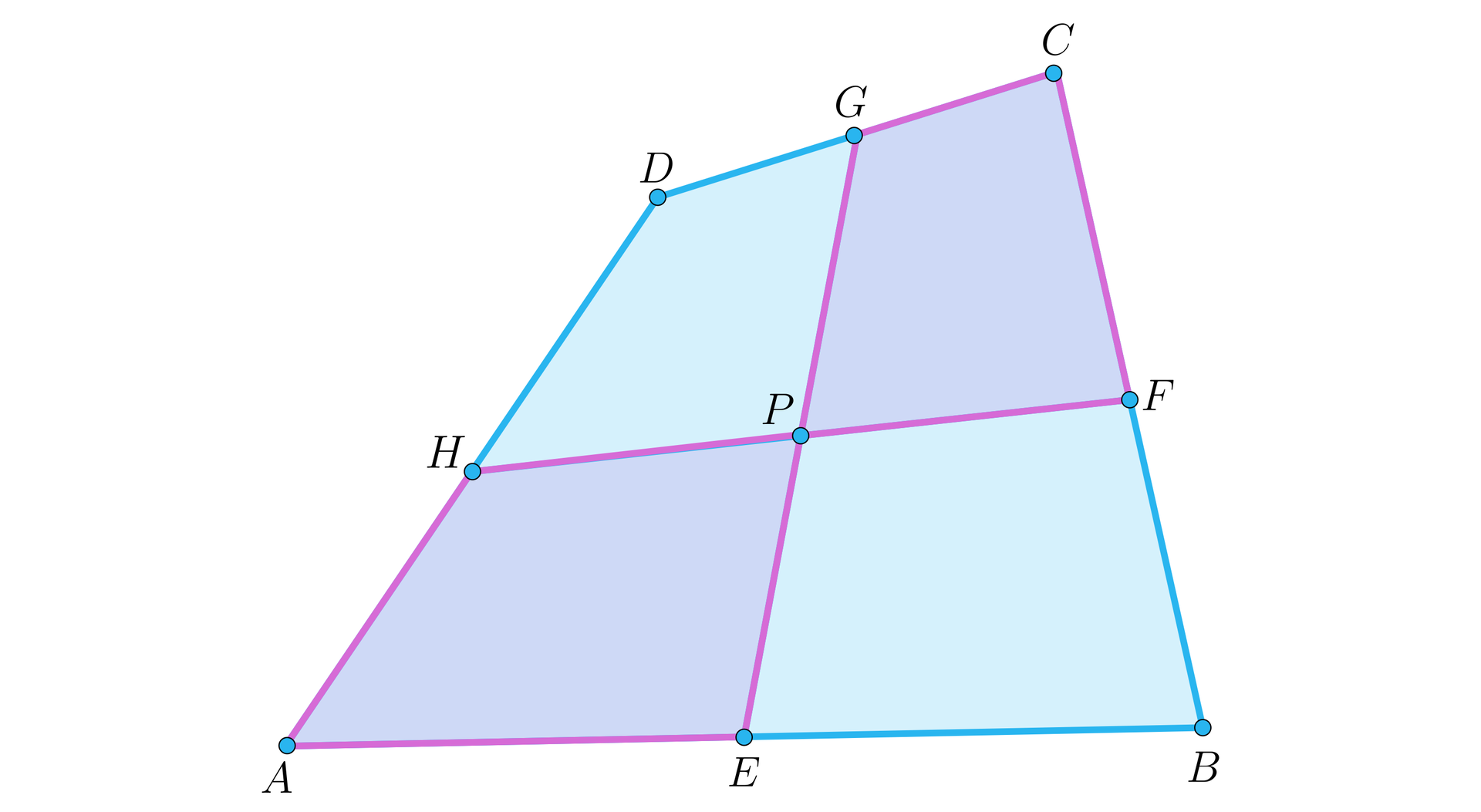
Rozwiązanie

R1eibKcpRpL6u

Na ilustracji przedstawiono czworokąt $ABCD$. Punkt E stanowi środek boku $AB$, punkt F stanowi środek boku $BC$, punkt G stanowi środek boku $DC$, oraz punkt H stanowi środek boku $AD$. Zaznaczono odcinki łączące punkty G i E, oraz H i F. W miejscu przecięcia się odcinków zaznaczono punkt P. Zacieniowano powstałe czworokąty $PGCF$, oraz $AHPE$. Linią przerywaną połączono wierzchołki czworokąta z punktem przecięcia P.

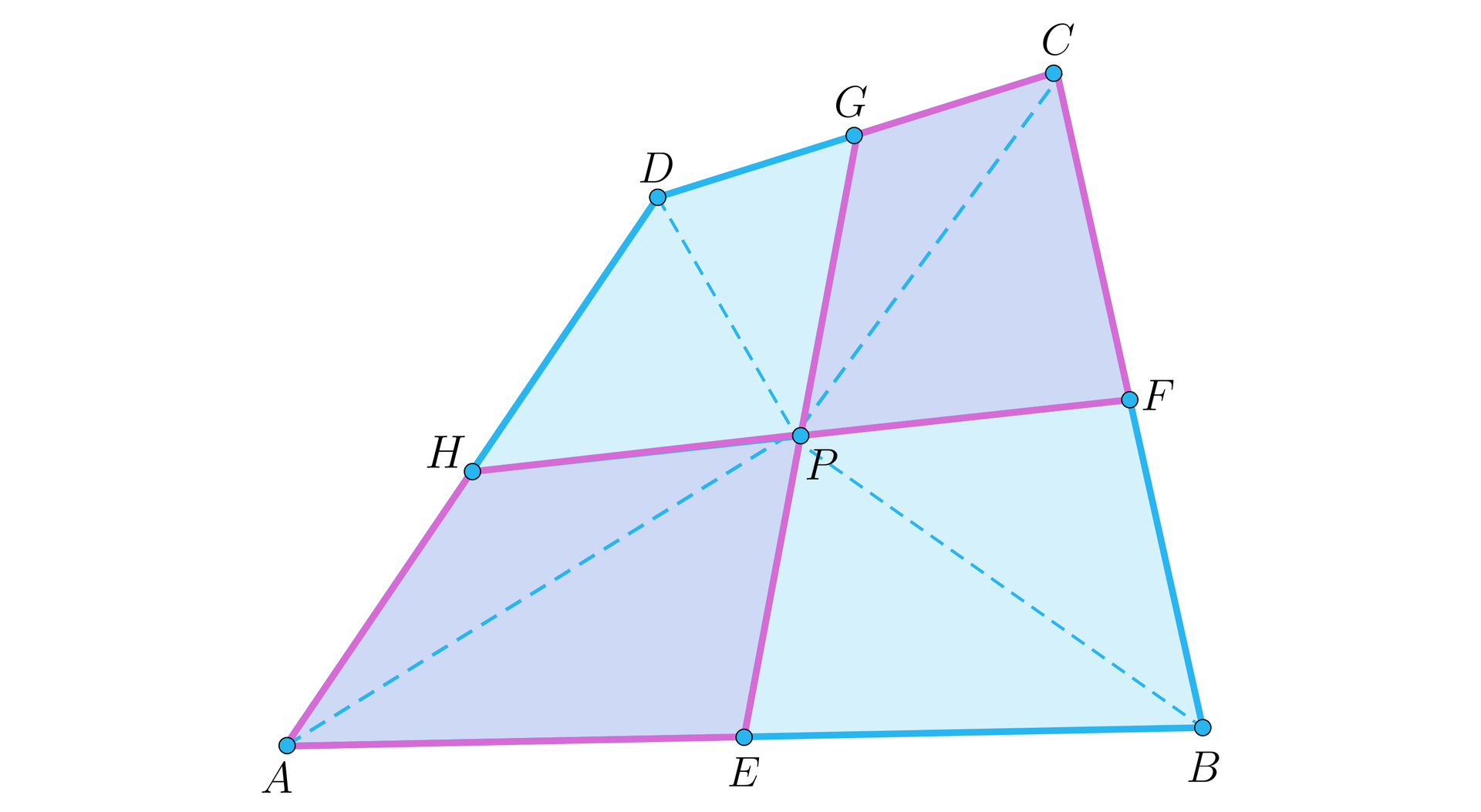
Z warunków zadania otrzymujemy równości następujących pól trójkątów:

$AEPiBEP$

$AHPiDHP$

$CFPiBFP$

$CGPiDGP$

Aby otrzymać tezę wystarczy dodać stronami  odpowiednie pola, wynikające z powyższej   równości:

$(P_{AEP}+P_{AHP})+(P_{CFP}+P_{CGP})=$

$=(P_{BEP}+P_{BFP})+(P_{DHP}+P_{DGP})$.

Zatem $P_{AEPH}+P_{PFCG}=P_{EBFP}+P_{HPGD}$.

wielokąt, którego boki tworzą zamkniętą łamaną (z czego wynika, że jest figurą spójną bez dziur), a dwa jego boki mają punkt wspólny tylko, gdy są sąsiadami

punkt, którego współrzędne w prostokątnym układzie współrzędnych są liczbami całkowitymi