Wyznaczymy obraz punktu $A=\left(1,-3\right)$ w symetrii względem punktu $S=\left(-3,4\right)$.

Oznaczmy szukane współrzędne przez $\left(x\text{'},y\text{'}\right)$. Możemy wykorzystać wzory wyprowadzone powyżej

$x\text{'}=2\cdot \left(-3\right)-1$ oraz $y\text{'}=2\cdot 4-\left(-3\right)$

$x\text{'}=-7$ oraz $y\text{'}=11$.

Wyznaczymy współrzędne $\left(a,b\right)$ środka symetrii, w której obrazem punktu $A=\left(-3,4\right)$ jest punkt $A\text{'}=\left(2,-3\right)$.

Możemy zauważyć, że środek symetrii jest środkiem odcinka o końcach $A$ i $A\text{'}$, zatem jego współrzędne są średnimi arytmetycznymi odpowiednich współrzędnych punktów $A$ i $A\text{'}$:

$a=\frac{x+x\text{'}}{2}=\frac{-3+2}{2}=\frac{-1}{2}=-\frac{1}{2}$ oraz $b=\frac{y+y\text{'}}{2}=\frac{4+\left(-3\right)}{2}=\frac{1}{2}$.

Wyznaczymy równanie figury, która jest obrazem figury $F$ o równaniu $\left|x-1\right|+\left|y+2\right|=1$ w symetrii względem punktu $S$ o współrzędnych $\left(-2,3\right)$.

Niech $A=\left(x,y\right)$ będzie dowolnym punktem należącym do figury $F$, zaś $A\text{'}=\left(x\text{'},y\text{'}\right)$ jego obrazem w symetrii względem punktu $S$.

Wówczas $A\text{'}=\left(x\text{'},y\text{'}\right)=\left(2\cdot \left(-2\right)-x,2\cdot 3-y\right)=\left(-4-x,6-y\right)$.

Zatem $x\text{'}=-4-x$ i $y\text{'}=6-y$.

Stąd $x=-4-x\text{'}$ oraz $y=6-y\text{'}$.

Możemy teraz podstawić $x=-4-x\text{'}$ oraz $y=6-y\text{'}$ do równania $\left|x-1\right|+\left|y+2\right|=1$ otrzymując $\left|-4-x\text{'}-1\right|+\left|6-y\text{'}+2\right|=1$, co po przekształceniach daje $\left|x\text{'}+5\right|+\left|y\text{'}-8\right|=1$.

Zmienne $x\text{'}$, $y\text{'}$ można zastąpić dowolnymi innymi, więc równanie można też zapisać w postaci $\left|x+5\right|+\left|y-8\right|=1$.

Zobaczmy jeszcze obie figury w układzie współrzędnych:

Równania figur	$\left|x-1\right|+\left|y+2\right|=1$	$\left|x+5\right|+\left|y-8\right|=1$
Figury	R1RFJkHvKqeCS Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus czterech do trzech oraz pionową osią $Y$ od minus trzech do siedmiu. Na płaszczyźnie narysowano czworokąt, którego wierzchołki stanowią punkty $\left(0;-2\right)$, $\left(1;-1\right)$, $\left(2;-2\right)$ oraz $\left(1;-3\right)$.	R19BMchQNLner Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus sześciu do jeden oraz pionową osią $Y$ od minus jeden do dziewięciu. Na płaszczyźnie narysowano czworokąt, którego wierzchołki stanowią punkty $\left(-6;8\right)$, $\left(-5;7\right)$, $\left(-4;8\right)$ oraz $\left(-5;9\right)$.

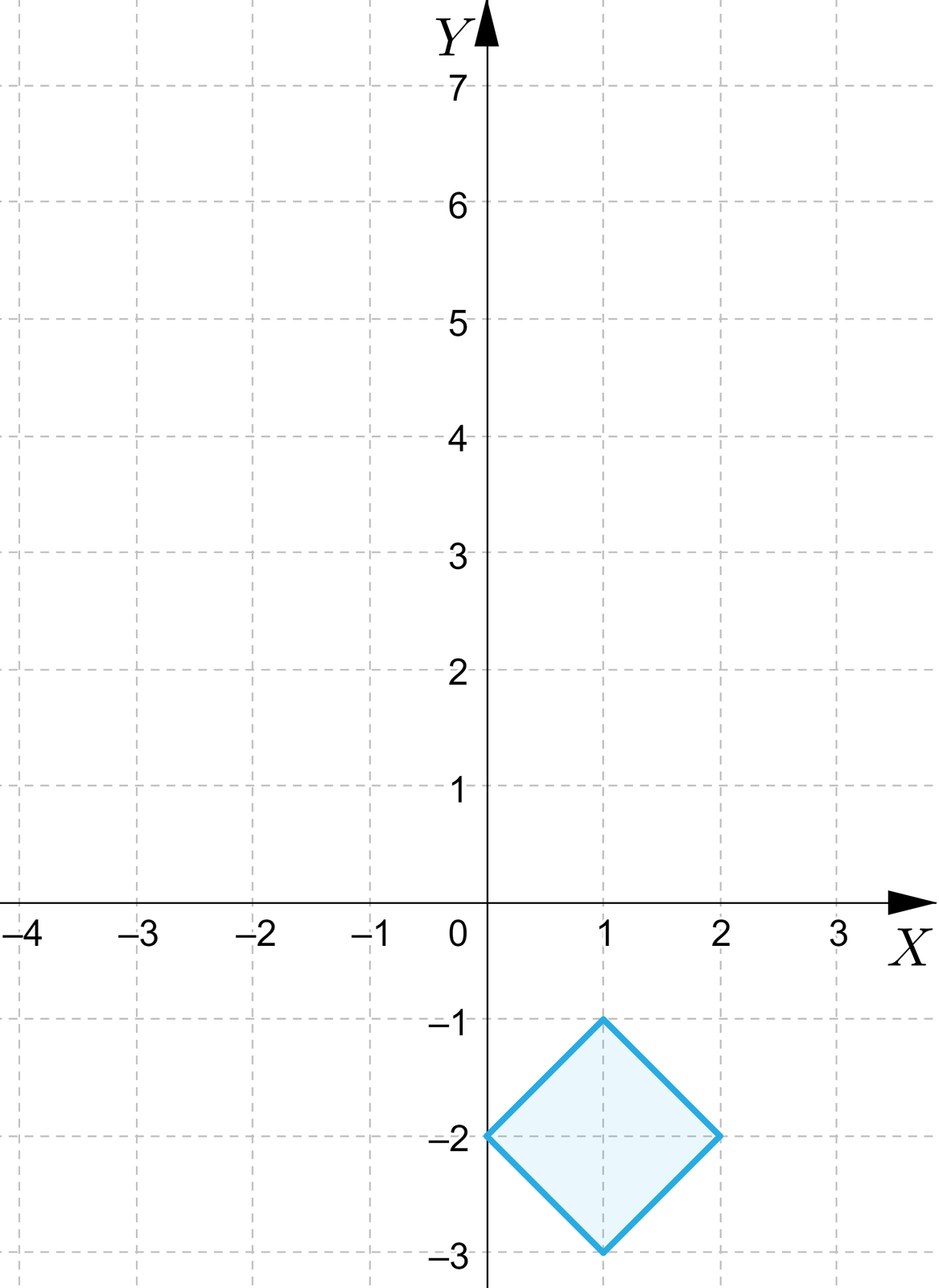Obie figury w jednym układzie współrzędnych:

RmihltJdHSNhT

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus siedmiu do trzech oraz pionową osią $Y$ od minus trzech do dziewięciu. Na płaszczyźnie narysowano dwa czworokąty. Czworokąt pierwszy leżący w czwartej ćwiartce układu współrzędnych o wierzchołkach $A\left(1;-3\right)$, $B\left(0;-2\right)$, $C\left(1;-1\right)$ oraz $D\left(2;o-2\right)$. Czworokąt drugi leżący w drugiej ćwiartce układu współrzędnych o wierzchołkach $A\text{'}\left(-5;9\right)$, $B\text{'}\left(-4;8\right)$, $C\text{'}\left(-5;7\right)$ oraz $D\text{'}\left(-6;8\right)$. Prostymi ukośnymi połączono ze sobą wierzchołki A i A prim, B i B prim, C i C prim oraz D i D prim. Środek symetrii znajduje się w punkcie S o współrzędnych $\left(-2;3\right)$.

Podsumujmy powyższy przykład. Jeśli dana figura opisuje się równaniem $f\left(x,y\right)=0$, to jej obraz w symetrii względem punktu o współrzędnych $\left(a,b\right)$ opisuje się równaniem $f\left(2a-x,2b-y\right)=0$.

Figura $F$ opisana jest równaniem ${\left(x+1\right)}^2+{\left(2y-1\right)}^2=1$. Wyznaczymy równanie obrazu figury $F$ w symetrii względem punktu o współrzędnych $\left(a,b\right)=\left(-2,1\right)$.

W tym celu w równaniu figury $F$ w miejsce zmiennej $x$ wstawimy wyrażenie $2\cdot \left(-2\right)-x=-4-x$, zaś w miejsce zmiennej $y$ wstawimy: $2\cdot 1-y=2-y$.

Otrzymujemy równanie ${\left(-4-x+1\right)}^2+{\left(2\left(2-y\right)-1\right)}^2=1$, czyli ${\left(-x-3\right)}^2+{\left(-2y+3\right)}^2=1$, po skorzystaniu z własności wartości bezwzględnej daje równanie ${\left(x+3\right)}^2+{\left(2y-3\right)}^2=1$.

Obie figury możemy narysować w układzie współrzędnych przy pomocy programu komputerowego:

RlGfWzmzEqGy1

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus pięciu do dwóch oraz pionową osią $Y$ od minus jeden do trzech. Na płaszczyźnie narysowano dwie elipsy leżące w drugiej ćwiartce układu współrzędnych. Elipsa pierwsza, na której zaznaczono punkty A B i C opisana jest równaniem ${\left(x+1\right)}^2+{\left(2y-1\right)}^2=1$. Na drugiej elipsie zaznaczono punkty A prim, B prim oraz C prim.Elipsę ta opisana jest równaniem ${\left(x+3\right)}^2+{\left(2y-3\right)}^2=1$. Zaznaczono proste ukośne łączące punkty A i A prim, B i B prim oraz C i C prim. Zaznaczono punkt S stanowiący środek symetrii.

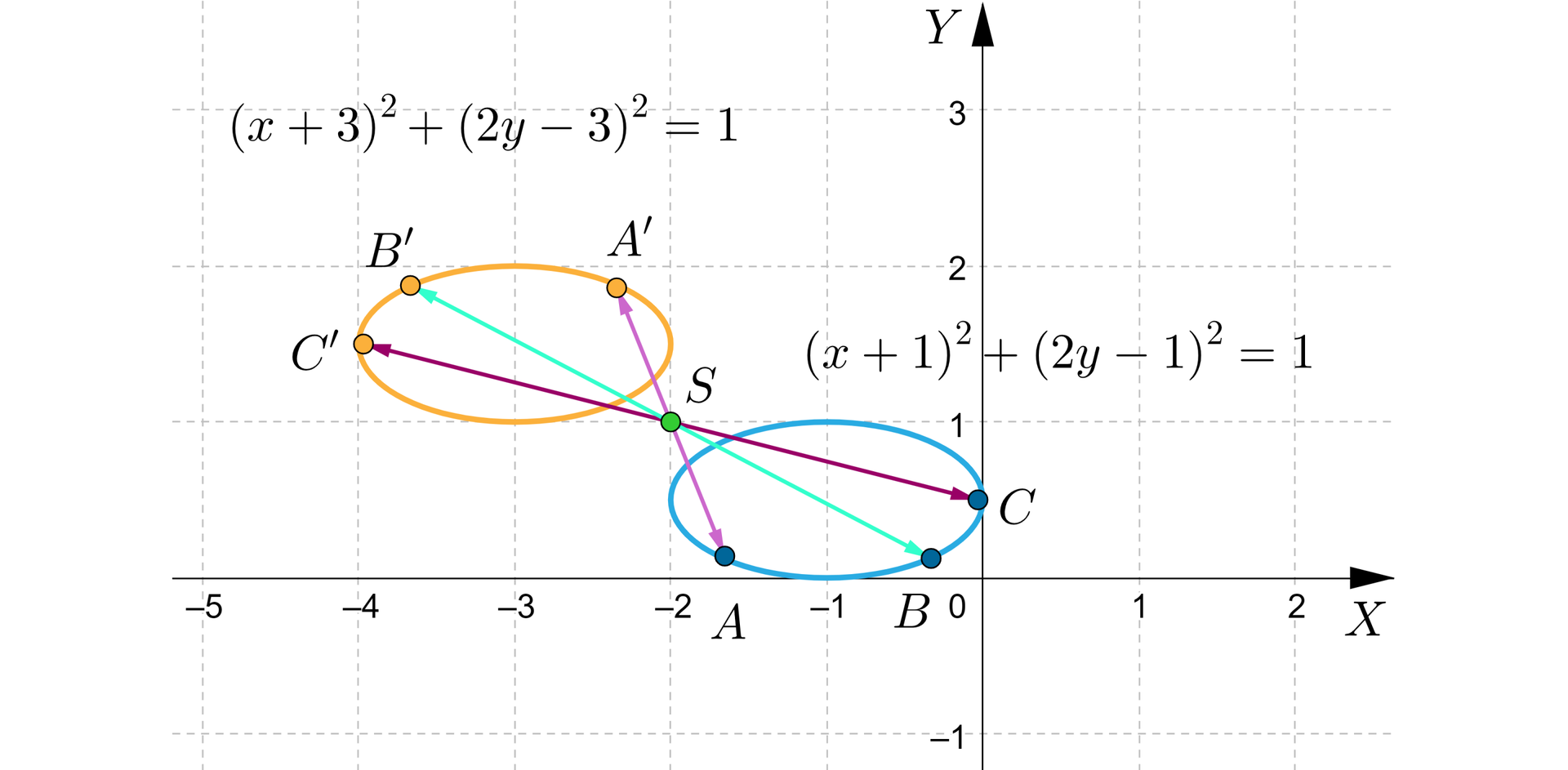
Symetria środkowa jest izometriąizometriaizometrią i inwolucją, więc posiada wszystkie wynikające z tego faktu własności:

• zachowuje długości odcinków,

• zachowuje miary kątów,

• zachowuje pola figur.

Ponadto symetria środkowa zachowuje orientację płaszczyzny, a jedynym punktem stałympunkt stały przekształceniapunktem stałym symetrii środkowej jest środek symetrii.

przekształcenie (płaszczyzny lub przestrzeni), które każdemu punktowi $A$ przyporządkowuje taki punkt $A\text{'}$, że punkt $S$ jest środkiem odcinka $AA\text{'}$; obrazem punktu $S$ jest punkt $S$; $S$ nazywamy środkiem symetrii

przekształcenie (płaszczyzny lub przestrzeni), które zachowuje długości odcinków, tzn. dla dowolnych punktów $A$, $B$ i ich obrazów w rozważanej izometrii $A\text{'}$, $B^{\prime }$ zachodzi

mówimy, że $A$ jest punktem stałym przekształcenia $P$, gdy obraz $A\text{'}$ punktu $A$ w przekształceniu $P$ pokrywa się z punktem $A$, czyli