Przeczytaj

Rozpocznijmy od podania następującej definicji.

prosta prostopadła do płaszczyzny

Definicja: prosta prostopadła do płaszczyzny

Mówimy, że prostaprosta prostopadła do płaszczyznyprosta $k$ jest prostopadła do płaszczyznyprosta prostopadła do płaszczyznyjest prostopadła do płaszczyzny $α$ (co zapisujemy symbolicznie w postaci $k ⊥ α$ ), jeżeli jest prostopadła do każdej prostej zawartej w płaszczyźnie $α$ .

Prawdziwe jest następujące twierdzenie o prostej prostopadłej do płaszczyznytwierdzenie o prostej prostopadłej do płaszczyzny.

o prostej prostopadłej do płaszczyzny

Twierdzenie: o prostej prostopadłej do płaszczyzny

Prosta prostopadła do dwóch przecinających się prostych jest prostopadła do płaszczyzny wyznaczonej przez te proste.

R1ZpC2rwMJEnj

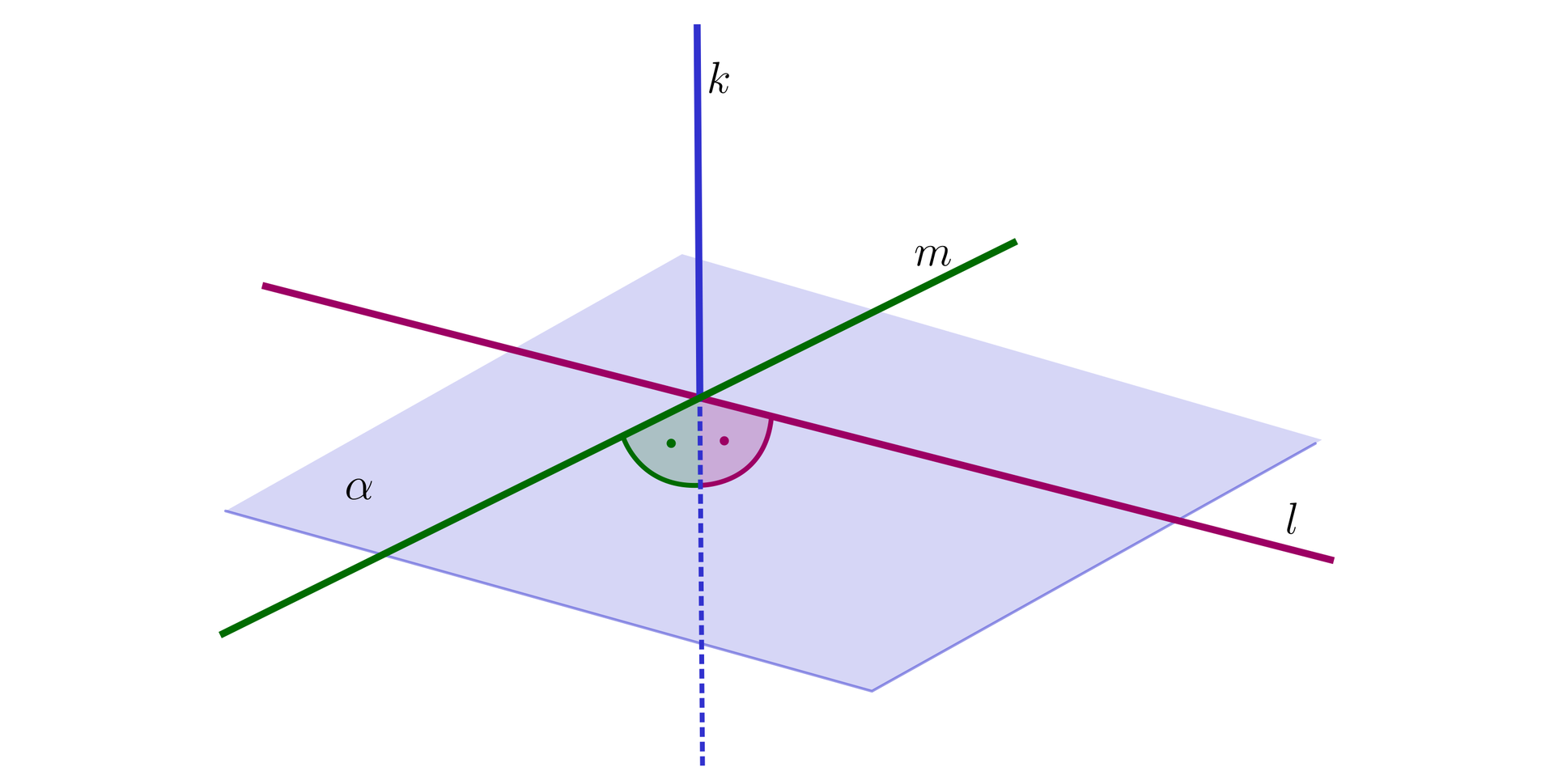
Ilustracja przedstawia płaszczyznę alfa przez którą przechodzi prosta k. Na płaszczyźnie leżą proste m oraz l, które przechodzą przez prostą k pod kątem prostym.

Dowód

Skoro prosta $k$ jest prostopadła do prostych $m$ i $l$ , to jest również prostopadła do każdej prostej równoległej do którejś z tych prostych.

Wystarczy zatem wykazać, że prosta $k$ jest prostopadła do dowolnej prostej przechodzącej przez punkt $O$ przecięcia prostych $m$ i $l$ . Oznaczmy tę prostą przez $n$ .

Poprowadźmy również prostą $t$ przecinającą proste $m$ , $l$ i $n$ odpowiednio w punktach $P$ , $Q$ i $S$ . Na prostej $k$ obierzmy punkty $A$ i $B$ , aby punkt $O$ był środkiem odcinka $A B$ .

R9zuOrdTYNFIG

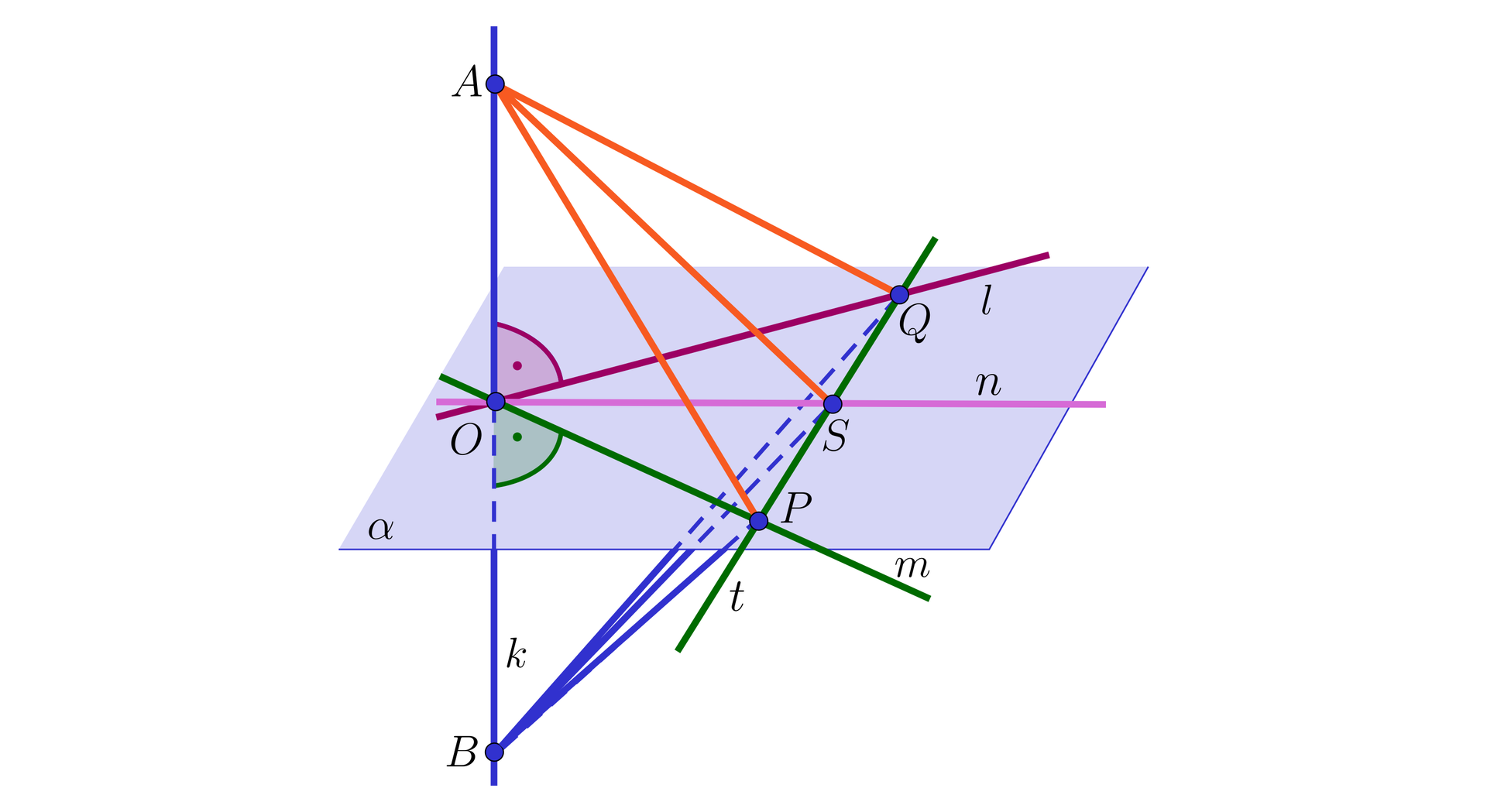
Ilustracja przedstawia płaszczyznę alfa przez którą przechodzi prosta k. Na prostej są zaznaczone trzy punkty, punkt: A, O i punkt B. Punkt O leży na płaszczyźnie, a punkt B pod płaszczyzną alfa. Przez prostą k w punkcie O przechodzą pod kątem prostym proste l, n, m. Na prostej l zaznaczono punkt Q, na prostej n zaznaczono punkt S, na prostej m zaznaczono punkt P. Przez punkty Q, S, P przechodzi prosta t. Z punktu A poprowadzono trzy odcinki, jeden do punktu Q, jeden do punktu S i jeden do punktu P. Analogicznie poprowadzono takie odcinki z punktu B.

Zauważmy, że proste $m$ i $l$ są symetralnymi odcinka $A B$ . Zatem: $|P A| = |P B|$ oraz $|Q A| = |Q B|$ . Stąd $△ P A Q \equiv △ P B Q$ (cecha $b b b$ ). To daje: $|∢ A P Q| = |∢ B P Q|$ .

Z równości wskazanych odcinków i kątów wynika, że $△ A P S \equiv △ B P S$ (cecha $b k b$ ). Zatem $|S A| = |S B|$ , czyli punkt $S$ leży na symetralnej $n$ odcinka $A B$ .

Ostatecznie $k ⊥ n$ , co kończy dowód.

Wniosek $1$

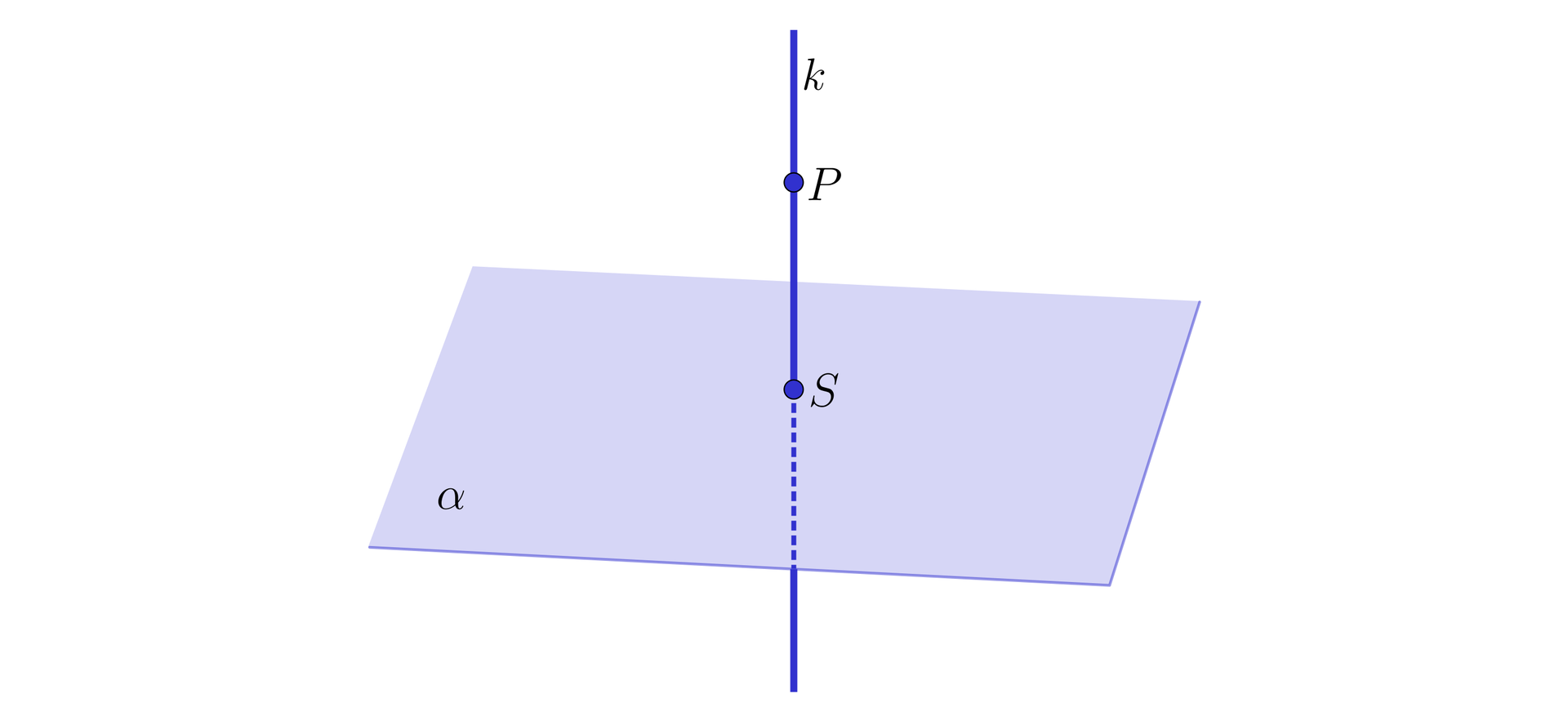
Niech $A$ będzie punktem wspólnym prostej $k$ i płaszczyzny $α$ .

Aby stwierdzić, że prosta $k$ jest prostopadła do płaszczyzny $α$ prosta prostopadła do płaszczyznyprosta $k$ jest prostopadła do płaszczyzny $α$ , wystarczy wskazać dwie proste leżące na tej płaszczyźnie i przechodzące przez punkt $A$ , do których prosta $k$ jest prostopadła.

rzut prostokątny punktu

Definicja: rzut prostokątny punktu

Rzutem prostokątnym punktu $P$ na płaszczyznę $α$ nazywamy punkt $S$ , w którym prosta $k$ przechodząca przez punkt $P$ i prostopadła do płaszczyzny $α$ przecina tę płaszczyznę.

Długość odcinka $P S$ jest odległością punktu $P$ od płaszczyzny $α$ .

R1aj9JgeJm7Gf

Ilustracja przedstawia płaszczyznę alfa przez którą przechodzi prosta k. Na prostej są zaznaczone trzy punkty, punkt: P i S. Punkt S leży na płaszczyźnie alfa.

rzut prostokątny figury

Definicja: rzut prostokątny figury

Rzutem prostokątnym figury $F$ na płaszczyznę nazywamy figurę wyznaczoną przez rzuty prostokątne wszystkich punktówrzuty prostokątne wszystkich punktów należących do tej figury.

punkt symetryczny do punktu A

Definicja: punkt symetryczny do punktu A

Punktem symetrycznym do punktu $A$ względem płaszczyzny $α$ nazywamy punkt $A'$ taki, że punkty $A$ i $A'$ leżą na prostej prostopadłej do płaszczyzny $α$ , w równych odległościach od płaszczyzny $α$ i po jej przeciwnych stronach.

Przykład 1

Rozważmy graniastosłup prosty $A B C D E F$ , którego podstawą jest trójkąt prostokątny $A B C$ .

R1On7n2rsWGLd

Ilustracja przedstawia graniastosłup trójkątny A B C D E F. Nad wierzchołkiem A znajduje się wierzchołek D, nad wierzchołkiem B wierzchołek E i nad wierzchołkiem C wierzchołek F. W podstawach znajduje się trójkąt prostokątny z kątem prostym przy wierzchołku C i F. Przez krawędź F i E przechodzi prosta k.

Uzasadnimy, że prosta $k$ przechodząca przez punkty $E$ i $F$ jest prostopadła do płaszczyzny zawierającej ścianę $A C F D$ .

Rozwiązanie

Prosta $k$ jest prostopadła do dwóch prostych $D F$ i $F C$ przecinających się w punkcie $F$ . Zatem na mocy twierdzenia o prostej prostopadłej do płaszczyzny otrzymujemy, że prosta $k$ przechodząca przez punkty $E$ i $F$ jest prostopadła do płaszczyzny zawierającej ścianę $A C F D$ .

Przykład 2

Rozważmy prostopadłościan $A B C D E F G H$ .

RPV3wN3CDCCFa

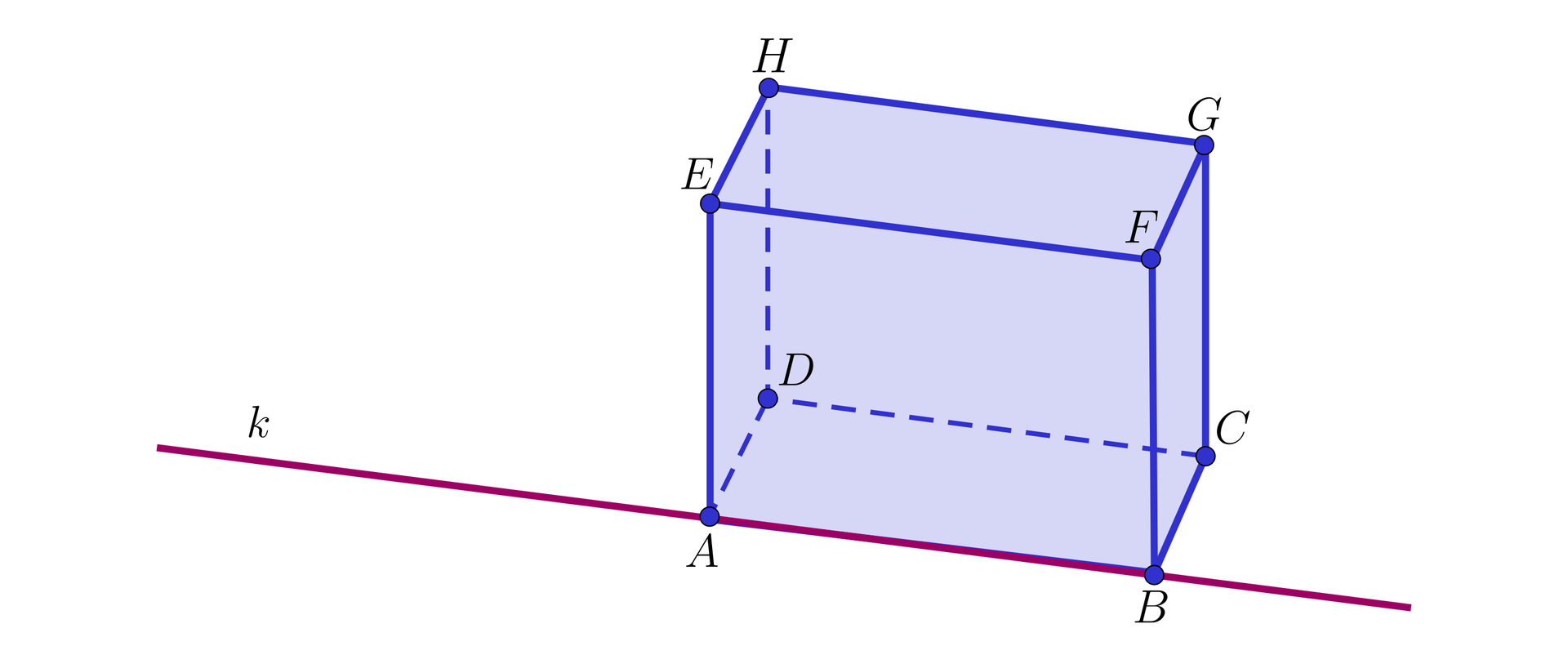
Ilustracja przedstawia prostopadłościan A B C D E F G H. Nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F, nad wierzchołkiem C wierzchołek G i nad wierzchołkiem D wierzchołek H. Przez krawędź AB przechodzi prosta k.

Uzasadnimy, że prosta $k$ przechodząca przez punkty $A$ i $B$ jest prostopadła do płaszczyzny zawierającej ścianę $B C G F$ .

Rozwiązanie

Prosta $k$ jest prostopadła do dwóch prostych $B C$ i $B F$ przecinających się w punkcie $B$ . Zatem na mocy twierdzenia o prostej prostopadłej do płaszczyzny otrzymujemy, że prosta $k$ przechodząca przez punkty $A$ i $B$ jest prostopadła do płaszczyzny zawierającej ścianę $B C G F$ .

Poniższy materiał wykracza poza wymagania podstawy programowej, ale jest ciekawym uzupełnieniem tej tematyki o ujęcie analityczne.

o równaniu prostej

Twierdzenie: o równaniu prostej

a) Prosta $p$ w przestrzeni przechodząca przez punkt $M (x_{0}, y_{0}, z_{0})$ i równoległa do wektora $\vec{a} = [l, m, n]$ (zwanego jej wektorem kierunkowym) może być przedstawiona w postaci parametrycznej:

$p :$ $\{\begin{cases} x = x_{0} + l t \\ y = y_{0} + m t, t \in ℝ \\ z = z_{0} + h t \end{cases}$ ,

$t$ nazywamy parametrem w równaniu prostej.

Równanie to może mieć postać $X = (x, y, z) = (x_{0}, y_{0}, z_{0}) + t \cdot (l, m, n)$ ,

lub, jeżeli $l$ , $m$ , $n$ $\neq 0$ , może być wyznaczone przez równania kanoniczne (równania kierunkowe):

$p :$ $\frac{x - x_{0}}{l} = \frac{y - y_{0}}{m} = \frac{z - z_{0}}{n}$

b) Przedstawienie parametryczne prostej $p$ w przestrzeni przechodzącej przez dwa dane punkty $M_{1} (x_{1}, y_{1}, z_{1})$ i $M_{2} (x_{2}, y_{2}, z_{2})$ jest postaci:

$p :$ $\{\begin{cases} x - x_{1} = t \cdot (x_{2} - x_{1}) \\ y - y_{1} = t \cdot (y_{2} - y_{1}), t \in ℝ \\ z - z_{1} = t \cdot (z_{2} - z_{1}) \end{cases}$

natomiast równania kanoniczne (kierunkowe) tej prostej są postaci:

$p :$ $\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}}$ .

o ogólnym układzie współrzędnych kartezjańskich

Twierdzenie: o ogólnym układzie współrzędnych kartezjańskich

a) W ogólnym układzie współrzędnych kartezjańskich w przestrzeni każda płaszczyzna $α$ określona jest równaniem postaci:

$A x + B y + C z = 0$ ,

gdzie liczby rzeczywiste $A$ , $B$ , $C$ nie zerują się jednocześnie (tzn. $A^{2} + B^{2} + C^{2} > 0$ ).

I na odwrót, każde takie równanie określa płaszczyznę i nazywa się jej równaniem ogólnym.

Wektor $\vec{v} = [A, B, C]$ nazywamy wektorem normalnym płaszczyzny $α$

Wektor normalny $\vec{v}$ jest prostopadły do płaszczyzny $α$ .

b) Równanie płaszczyzny $α$ przechodzącej przez trzy punkty $M_{1} (x_{1}, y_{1}, z_{1})$ , $M_{2} (x_{2}, y_{2}, z_{2})$ , $M_{3} (x_{3}, y_{3}, z_{3})$ nie leżące na jednej prostej ma postać parametryczną.

$α :$ $\{\begin{cases} x = x_{1} + u \cdot (x_{2} - x_{1}) + v \cdot (x_{3} - x_{1}) \\ y = y_{1} + u \cdot (y_{2} - y_{1}) + v \cdot (y_{3} - y_{1}), t \in ℝ \\ z = z_{1} + u \cdot (z_{2} - z_{1}) + v \cdot (z_{3} - z_{1}) \end{cases}$

( $u$ , $v$ są parametrami, w tym równaniu płaszczyzny)

o równoległości płaszczyzn

Twierdzenie: o równoległości płaszczyzn

a) Na to, aby dwie płaszczyzny $α :$ $A_{1} x + B_{1} y + C_{1} z + D_{1} = 0$ i $β :$ $A_{2} x + B_{2} y + C_{2} z + D_{2} = 0$ były równoległe potrzeba i wystarcza, aby odpowiednie współczynniki przy $x$ , $y$ , $z$ były proporcjonalne:

$\{\begin{cases} A_{2} = λ \cdot A_{1} \\ B_{2} = λ \cdot B_{1}, przy czym D_{2} \neq λ \cdot D_{1} \\ C_{2} = λ \cdot C_{1} \end{cases}$

b) Na to, aby dwie płaszczyzny $α :$ $A_{1} x + B_{1} y + C_{1} z + D_{1} = 0$ i $β :$ $A_{2} x + B_{2} y + C_{2} z + D_{2} = 0$ pokrywały się potrzeba i wystarcza, aby odpowiednie współczynniki ich równań ogólnych były proporcjonalne, tzn.

$\{\begin{cases} A_{2} = λ \cdot A_{1} \\ B_{2} = λ \cdot B_{1} \\ C_{2} = λ \cdot C_{1} \\ D_{2} = λ \cdot D_{1} \end{cases}$ , gdzie $λ \neq 0$

czyli $A_{2} x + B_{2} y + C_{2} z + D_{2} \equiv λ \cdot (A_{1} x + B_{1} y + C_{1} z + D_{1})$ , gdzie $λ \neq 0$ (tożsamość ze względu na $x$ , $y$ , $z$ ).

o przecinaniu się płaszczyzn nierównoległych do siebie

Twierdzenie: o przecinaniu się płaszczyzn nierównoległych do siebie

Każde dwie płaszczyzny nierównoległe do siebie w przestrzeni przecinają się wzdłuż prostej.

Prosta w przestrzeni może więc być przedstawiona przez podanie dowolnych dwóch różnych płaszczyzn przecinających się wzdłuż prostej.

Wypisując równania ogólne tych płaszczyzn otrzymujemy tzw. równanie krawędziowe prostej $p$ w przestrzeni postaci:

$p :$ $\{\begin{cases} A_{1} x + B_{1} y + C_{1} z + D_{1} = 0 \\ A_{2} x + B_{2} y + C_{2} z + D_{2} = 0 \end{cases}$

o prostej prostopadłej do płaszczyzny w kartezjańskim układzie współrzędnych

Twierdzenie: o prostej prostopadłej do płaszczyzny w kartezjańskim układzie współrzędnych

Niech $p$ będzie prostą w przestrzeni równoległą do wektora $\vec{a} = [l, m, n]$ .

Niech $A x + B y + C z + D = 0$ będzie równaniem ogólnym płaszczyzny $α$ .

Na to, aby prosta $p$ była prostopadła do płaszczyzny $α$ (w kartezjańskim układzie współrzędnych w przestrzeni) potrzeba i wystarcza, aby:

$\{\begin{cases} A = λ \cdot l \\ B = λ \cdot m, gdzie λ \neq 0 \\ C = λ \cdot n \end{cases}$

Przykład 3

Wyznaczymy równania rzutu prostej

$p :$ $\{\begin{cases} 2 x + y - 2 + 4 = 0 \\ x + y = 0 \end{cases}$

na płaszczyznę $O_{x z}$

Rozwiązanie

Wyznaczymy najpierw równanie parametryczne prostej $p$ .

Z treści zadania mamy, że równanie krawędziowe prostej $p$ jest postaci:

$\{\begin{cases} 2 x + y - z + 4 = 0 \\ x + y = 0 \end{cases}$

Niech $x = t$ .

Wtedy dostajemy:

$\{\begin{cases} 2 t + y - 2 + 4 = 0 \\ t + y = 0 \end{cases}$

$y = (- t)$

Dalej mamy:

$2 t - t - z + 4 = 0$

$t - z + 4 = 0$

$z = t + 4$

Dlatego równanie parametryczne prostej $p$ jest postaci:

$p :$ $\{\begin{cases} x = t \\ y = (- t), t \in ℝ \\ z = 4 + t \end{cases}$

Płaszczyzna $O_{x z}$ jest opisana równaniem ogólnym $y = 0$ .

Rzutem prostej $p$ na płaszczyźnie $O_{x z}$ jest prosta leżąca w tej płaszczyźnie, tzn. spełniającej warunek $y = 0$ .

Dlatego równanie parametryczne tego rzutu jest postaci:

$\{\begin{cases} x = t \\ y = 0, t \in ℝ \\ z = 4 + t \end{cases}$

Przykład 4

Napiszemy równania prostej $p$ przechodzącej przez punkt $M (x_{0}, y_{0}, z_{0})$ i prostopadłej do płaszczyzny $α : A x + B y + C z + D = 0$ .

Rozwiązanie

Wektorem normalnym płaszczyzny $α$ jest $\vec{v} = [A, B, C]$

Niech $p$ będzie szukaną prostą w przestrzeni równoległą do wektora $\vec{a} = [l, m, n]$ .

Wtedy na mocy twierdzenia o prostej prostopadłej do płaszczyzny w kartezjańskim układzie współrzędnych dostajemy, że prosta $p$ jest prostopadła do płaszczyzny $α$ wtedy i tylko wtedy, gdy

$\{\begin{cases} A = λ \cdot l \\ B = λ \cdot m, gdzie λ \neq 0 \\ C = λ \cdot n \end{cases}$

Przyjmijmy $λ = 1$

Wtedy:

$\{\begin{cases} I = A \\ m = B \\ n = C \end{cases}$

Czyli $\vec{a} = \vec{v} = [A, B, C]$

Dlatego równanie parametryczne prostej $p$ jest postaci

$p :$ $\{\begin{cases} x = x_{0} + A t \\ y = y_{0} + B t, t \in ℝ \\ z = z_{0} + C t \end{cases}$

Słownik

prosta prostopadła do płaszczyzny

prosta prostopadła do każdej prostej zawartej w tej płaszczyźnie

twierdzenie o prostej prostopadłej do płaszczyzny

jeżeli prosta $k$ jest prostopadła do dwóch przecinających się prostych $l$ i $n$ , to prosta $k$ jest prostopadłą do płaszczyzny $α$ wyznaczonej przez te proste

rzut prostokątny punktu na płaszczyznę

rzutem prostokątnym punktu $P$ na płaszczyznę nazywamy punkt przecięcia tej płaszczyzny z prostą przechodzącą przez punkt $P$ i prostopadłą do tej płaszczyzny

Wprowadzenie

Aplet

Słownik