Układem równań liniowych z dwiema niewiadomymi nazywamy koniunkcję dwóch równań pierwszego stopnia z dwiema niewiadomymi.

Układ taki przyjmuje postać:

gdzie $a_1$ i $b_1$ oraz $a_2$ i $b_2$ nie są równocześnie równe zero. W powyższym układzie $x$ oraz $y$ to niewiadome, $a_1$, $a_2$, $b_1$ oraz $b_2$ - współczynniki przy niewiadomych odpowiednio $x$ oraz $y$, natomiast $c_1$ i $c_2$ nazywamy wyrazami wolnymi.

Rozwiązaniem  takiego układu równań z dwiema niewiadomymi  jest każda  para liczb spełniających jednocześnie wszystkie równania  układu.

Przy czym taki układ równań może nie  mieć rozwiązania lub  może mieć jedno rozwiązanie,  lub nawet nieskończenie wiele rozwiązań.

Układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest dokładnie jedna para liczb, nazywamy układem oznaczonym.

Układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest nieskończenie wiele par liczb, nazywamy układem nieoznaczonym.

Układ równań liniowych z dwiema niewiadomymi, który nie posiada rozwiązań, nazywamy układem sprzecznym.

Dwa układy równań liniowych (z tymi samymi niewiadomymi) nazywamy równoważnymi, gdy mają ten sam zbiór rozwiązań.

Jeśli obie strony każdego z równań (lub jednego z nich) danego układu równań pomnożymy przez dowolne liczby różne od zera, a następnie równania te dodamy stronami i tak otrzymanym równaniem zastąpimy jedno z równań układu, to otrzymany układ równań jest równoważny danemurównoważne układy równańukład równań jest równoważny danemu.

Ten fakt wykorzystujemy rozwiązując układy równań metodą przeciwnych współczynników – mnożymy jedno z równań przez taką liczbę, by współczynniki przy jednej ze zmiennych były liczbami przeciwnymi a następnie dodajemy równania stronami.

Rozwiążemy układ równań liniowych metodą przeciwnych współczynników.

$\left\{\begin{array}{l}2x+3y=-1\\ 2y+3x=2 \end{array}\right.$

Porządkujemy kolejność niewiadomych w układzie równań.

$\left\{\begin{array}{l}2x+3y=-1\\ 3x+2y=2\end{array}\right.$

Mnożymy obie strony pierwszego równania przez liczbę $\left(-3\right)$, a obie strony drugiego równania przez liczbę $2$.

$\left\{\begin{array}{l}2x+3y=-1 |·\left(-3\right)\\ 3x+2y=2 |·2 \end{array}\right.$

Wówczas współczynniki liczbowe przy niewiadomej $x$ będą liczbami przeciwnymi.

Otrzymane równania dodajemy stronami.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}-6x-9y=3\\ 6x+4y=4\end{array}\right.} \\ -5y=7 \overline{):\left(-5\right)} \end{gathered}$$

Rozwiązujemy równanie z niewiadomą $y$.

$y=-1\frac{2}{5}$

Otrzymanym w ten sposób równaniem możemy zastąpić pierwsze z równań układu.

$\left\{\begin{array}{l}y=-1\frac{2}{5}\\ 3x+2y=2\end{array}\right.$

Postawiamy otrzymaną wartość $y$ do drugiego z równań układu.

$\left\{\begin{array}{l}y=-1\frac{2}{5}\\ 3x-2·1\frac{2}{5}=2\end{array}\right.$

Rozwiązujemy drugie równanie.

$\left\{\begin{array}{l}y=-1\frac{2}{5}\\ 3x-2\frac{4}{5}=2\end{array}\right.$

$\left\{\begin{array}{l}y=-1\frac{2}{5}\\ 3x=2+2\frac{4}{5}\end{array}\right.$

$\left\{\begin{array}{l}y=-1\frac{2}{5}\\ x=4\frac{4}{5}:3\end{array}\right.$

Otrzymaliśmy parę liczb będącą rozwiązaniem danego układu równań.

$\left\{\begin{array}{l}x=\frac{8}{5}\\ y=-1\frac{2}{5}\end{array}\right.$

(Sprawdź!)

Zauważmy, że ten sam układ równań liniowychukład równań liniowych z dwiema niewiadomymiukład równań liniowych możemy rozwiązać redukując niewiadomą $y$.

$\left\{\begin{array}{l}2x+3y=-1\\ 3x+2y=2\end{array}\right.$

Mnożymy obie strony pierwszego równania przez liczbę $\left(-2\right)$, a obie strony drugiego równania przez liczbę $3$.

$\left\{\begin{array}{l}2x+3y=-1 |·\left(-2\right)\\ 3x+2y=2 |·3\end{array}\right.$

Wówczas współczynniki przy niewiadomej $y$ będą liczbami przeciwnymi.

Otrzymane równania dodajemy stronami.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}-4x-6y=2\\ 9x+6y=6\end{array}\right.} \\ 5x=8 \overline{):5} \end{gathered}$$

Rozwiązujemy równanie z niewiadomą $x$.

$x=\frac{8}{5}$

Otrzymanym w ten sposób równaniem możemy zastąpić pierwsze z równań układu.

$\left\{\begin{array}{l}x=\frac{8}{5}\\ 3x+2y=2\end{array}\right.$

Postawiamy otrzymaną wartość $x$ do drugiego z równań układu.

$\left\{\begin{array}{l}x=\frac{8}{5}\\ 3·\frac{8}{5}+2y=2\end{array}\right.$

Rozwiązujemy drugie równanie.

$\left\{\begin{array}{l}x=\frac{8}{5}\\ \frac{24}{5}+2y=2\end{array}\right.$

$\left\{\begin{array}{l}x=\frac{8}{5}\\ 2y=2-4\frac{4}{5}\end{array}\right.$

$\left\{\begin{array}{l}x=\frac{8}{5}\\ y=-1\frac{2}{5}\end{array}\right.$

Otrzymaliśmy parę liczb będącą rozwiązaniem danego układu równań.

$\left\{\begin{array}{l}x=\frac{8}{5}\\ y=-1\frac{2}{5}\end{array}\right.$.

Korzystając z metody przeciwnych współczynników, wyznaczymy liczbę rozwiązań układów równań liniowych.

a) $\left\{\begin{array}{l}3x+12y=4\\ -x-4y=4\end{array}\right.$

$\left\{\begin{array}{l}3x+12y=4\\ -x-4y=4 |·3\end{array}\right.$

$$\begin{gathered} \underline{+\left\{\begin{array}{l}3x+12y=4\\ -3x-12y=12\end{array}\right.} \\ 0=16 \end{gathered}$$

Jest to układ sprzecznyukład równań sprzecznyukład sprzeczny. Taki układ równań nie posiada rozwiązań.

b) $\left\{\begin{array}{l}-2x+6y=10\\ x-3y=-5\end{array}\right.$

$\left\{\begin{array}{l}-2x+6y=10\\ x-3y=-5 |·2\end{array}\right.$

$$\begin{gathered} \underline{+\left\{\begin{array}{l}-2x+6y=10 \\ 2x-6y=-10\end{array}\right.} \\ 0=0 \end{gathered}$$

Jest to układ nieoznaczonyukład równań nieoznaczonyukład nieoznaczony. Posiada on nieskończenie wiele rozwiązań postaci

$\left\{\begin{array}{l}x \in \mathrm{ℝ}\\ y=\frac{1}{3}x+\frac{5}{3}\end{array}\right.$.

c) $\left\{\begin{array}{l}x-4y=3\\ 2x-3y=1\end{array}\right.$

Redukujemy niewiadomą $x$.

$\left\{\begin{array}{l}x-4y=3 |·\left(-2\right)\\ 2x-3y=1\end{array}\right.$

Dodajemy równania stronami.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}-2x+8y=-6\\ 2x-3y=1\end{array}\right.} \\ 5y=-5 \end{gathered}$$

Obliczmy wartość niewiadomej $y$.

$y=-1$

$\left\{\begin{array}{l}x-4y=3\\ y=-1\end{array}\right.$

Podstawimy otrzymaną wartość $y$ do pierwszego równania i obliczamy niewiadomą $x$.

$\left\{\begin{array}{l}x-4·\left(-1\right)=3\\ y=-1\end{array}\right.$

$\left\{\begin{array}{l}x+4=3\\ y=-1\end{array}\right.$

$\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$

Jest to układ oznaczonyukład równań oznaczonyukład oznaczony. Posiada on jedno rozwiązanie postaci $\left\{\begin{array}{l}x=-1\\ y=-1\end{array}\right.$.

Rozwiążemy układ równań liniowych metodą przeciwnych współczynników

$\left\{\begin{array}{l}\frac{-5x+3y}{5}-\frac{x-y}{2}=1\\ 4\left(x+2\right)-5\left(2-y\right)=7x-y\end{array}\right.$.

Aby móc zastosować tę metodę, musimy doprowadzić układ równań do najprostszej postaci. Możemy więc pomnożyć obie strony pierwszego równania przez $10$.

$\left\{\begin{array}{l}2\left(-5x+3y\right)-5\left(x-y\right)=10·1\\ 4\left(x+2\right)-5\left(2-y\right)=7x-y\end{array}\right.$

W każdym z równań usuwamy nawiasy, redukujemy wyrażenia podobne i porządkujemy układ.

$\left\{\begin{array}{l}-10x+6y-5x+5y=10\\ 4x+8-10+5y=7x-y\end{array}\right.$

$\left\{\begin{array}{l}-15x+11y=10\\ -3x+6y=2\end{array}\right.$

Mnożymy teraz obie strony drugiego równania przez liczbę $\left(-5\right)$, aby otrzymać przeciwne współczynniki przy niewiadomej $x$.

$\left\{\begin{array}{l}-15x+11y=10\\ 15x-30y=-10\end{array}\right.$

Dodajemy równania stronami.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}-15x+11y=10\\ 15x-30y=-10\end{array}\right.} \\ -19y=0 \end{gathered}$$

$y=0$

Otrzymane wyrażenie  wstawiamy do układu $\left\{\begin{array}{l}-15x+11y=10\\ -3x+6y=2\end{array}\right.$ w miejsce pierwszego równania.

Następnie obliczamy niewiadomą $x$.

$\left\{\begin{array}{l}y=0\\ -3x+6y=2\end{array}\right.$

$\left\{\begin{array}{l}y=0\\ -3x-0=2\end{array}\right.$

$\left\{\begin{array}{l}y=0\\ x=-\frac{2}{3}\end{array}\right.$

Otrzymaliśmy parę liczb $\left\{\begin{array}{l}x=-\frac{2}{3}\\ y=0\end{array}\right.$, będącą rozwiązaniem tego układu równań.

Zauważmy, że stosując tę metodę, pomimo dużych liczb pojawiających się w układzie równań

$\left\{\begin{array}{l}-15x+11y=10\\ -3x+6y=2\end{array}\right.$

udało się nam sprawnie znaleźć jego rozwiązanie.

Obliczymy długości boków trójkąta równoramiennego $ABC$ przedstawionego na poniższym rysunku, wiedząc, że podstawa $AB$ jest o $5$ dłuższa od jednego z  ramion.

R1P8rJWvawnd1

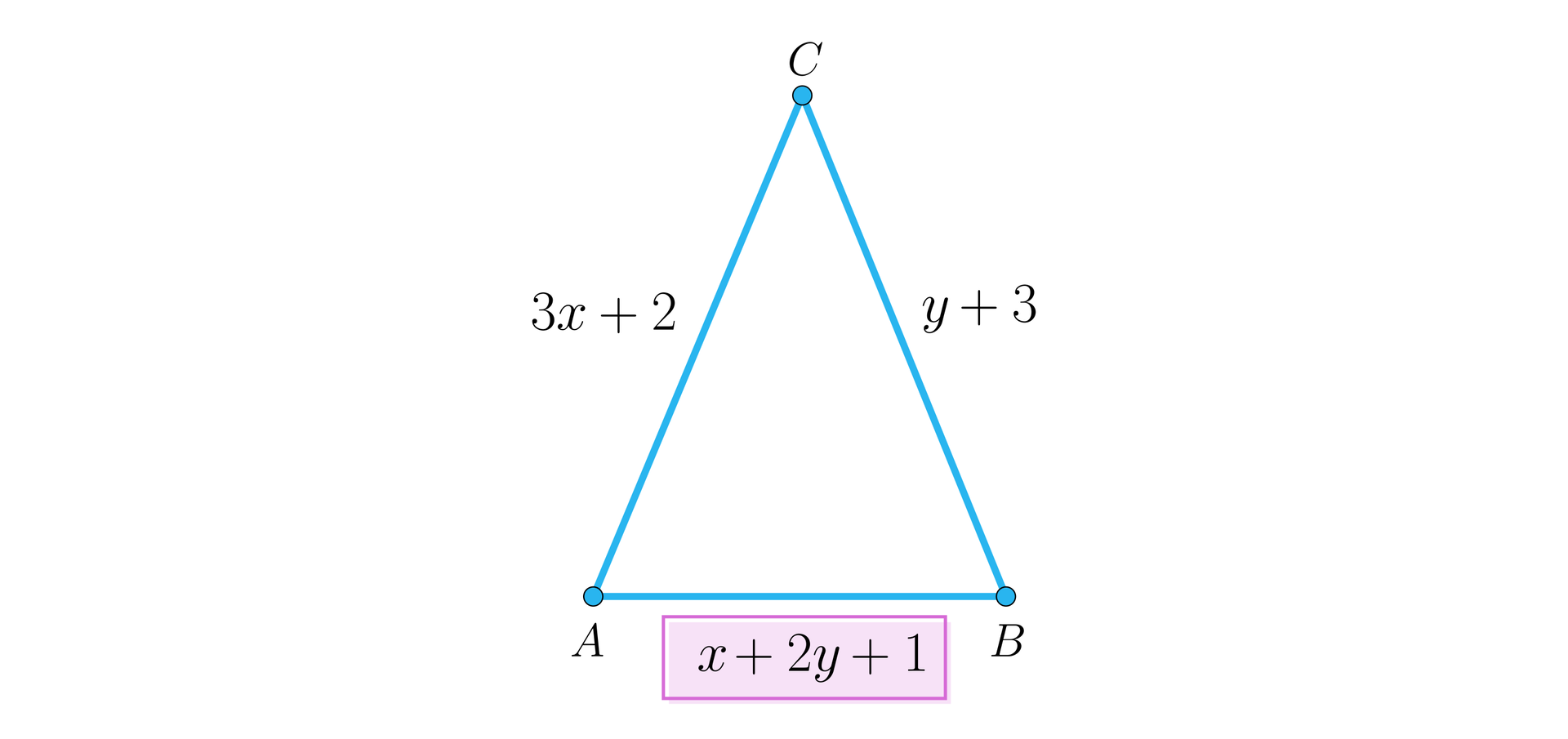
Zapisujemy i porządkujemy odpowiedni układ równań.

$\left\{\begin{array}{l}3x+2=y+3\\ x+2y+1=y+3+5\end{array}\right.$

$\left\{\begin{array}{l}3x-y=3-2\\ x+2y-y=8-1\end{array}\right.$

$\left\{\begin{array}{l}3x-y=1\\ x+y=7\end{array}\right.$

W tym układzie równań, przed niewiadomą $y$ znajdują się przeciwne współczynniki, a zatem możemy dodać równania stronami i rozwiązać ten układ metodą przeciwnych współczynnikówmetoda przeciwnych współczynnikówmetodą przeciwnych współczynników.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}3x-y=1\\ x+y=7\end{array}\right.} \\ 4x=8 \end{gathered}$$

$x=2$

Obliczamy teraz niewiadomą $y$.

$\left\{\begin{array}{l}x=2\\ x+y=7\end{array}\right.$

$\left\{\begin{array}{l}x=2\\ 2+y=7\end{array}\right.$

$\left\{\begin{array}{l}x=2\\ y=5\end{array}\right.$

Możemy teraz obliczyć długości boków trójkąta $ABC$.

$\left|AB\right|=x+2y+1=13$

$\left|BC\right|=y+3=8$

$\left|AC\right|=3x+2=8$.

Zbadamy, dla jakich wartości parametru $k$, rozwiązaniami układu równań

$\left\{\begin{array}{l}2x+y=k+1\\ x-2y=k\end{array}\right.$

są pary liczb dodatnich.

Aby wyznaczyć rozwiązanie układu równań, możemy pomnożyć drugie równanie przez liczbę $\left(-2\right)$. Otrzymamy wtedy przeciwne współczynniki przy niewidomej $x$.

$\left\{\begin{array}{l}2x+y=k+1\\ x-2y=k |·\left(-2\right)\end{array}\right.$

$\left\{\begin{array}{l}2x+y=k+1\\ -2x+4y=-2k\end{array}\right.$

Dodajemy równania stronami i wyznaczamy niewiadomą $y$.

$$\begin{gathered} \underline{+\left\{\begin{array}{l}2x+y=k+1\\ -2x+4y=-2k\end{array}\right.} \\ 5y=1-k \end{gathered}$$

$y=\frac{1-k}{5}$

Możemy zastąpić otrzymaną równością pierwsze z równań układu. Następnie wyznaczamy niewiadomą $x$.

$\left\{\begin{array}{l}y=\frac{1-k}{5}\\ x-2y=k\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1-k}{5}\\ x-2·\frac{1-k}{5}=k\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1-k}{5}\\ x=k+2·\frac{1-k}{5}\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1-k}{5}\\ x=\frac{5k}{5}+\frac{2-2k}{5}\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1-k}{5}\\ x=\frac{2+3k}{5}\end{array}\right.$

Sprawdzamy dla jakich $k$ liczby $x$ i $y$ są liczbami dodatnimi.

$y=\frac{1-k}{5}>0\iff 1-k>0\iff k<1$

$x=\frac{2+3k}{5}>0\iff 2+3k>0\iff k>-\frac{2}{3}$

A zatem $\left\{\begin{array}{l}y>0\\ x>0\end{array}\right.\iff k\in \left(-\frac{2}{3}, 1\right)$.

układ równań postaci

układy równań, które mają ten sam zbiór rozwiązań

układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest dokładnie jedna para liczb

układ równań liniowych z dwiema niewiadomymi, którego rozwiązaniem jest nieskończenie wiele par liczb

układ równań liniowych z dwiema niewiadomymi, który nie posiada rozwiązań

metoda polegająca na pomnożeniu obu stron jednego lub każdego równania przez dowolną liczbę różną od zera, tak aby przy jednej z niewiadomych otrzymać przeciwne współczynniki, dzięki czemu po dodaniu do siebie równań stronami można obliczyć jedną z niewiadomych