Przeczytaj
Granice niewłaściwe w kosmosie
Granicę funkcji w punkcie nazywamy właściwą, gdy jest liczbą (skończoną), natomiast niewłaściwą, jeżeli jest równa nieskończoności. Wydawałoby się, że poza abstrakcyjną częścią matematyki, w jej zastosowaniach nie powinniśmy otrzymywać w wyniku granic nieskończonych.
Przyjrzyjmy się zatem, odkrytemu przez Alberta Einsteina, zjawisku dylatacji czasu. Nie wchodząc w szczegóły z zakresu fizyki, dylatacja czasu oznacza, że jeżeli ktoś porusza się z dużą prędkością, porównywalną z prędkością światła, to w porównaniu z osobą, która się nie porusza, dla podróżnika czas będzie płynął znacznie wolniej. Możemy na odwrót powiedzieć, że dla osoby, która pozostała nieruchomo, czas będzie płynął znacznie szybciej, niż dla tej, która się porusza.
Zależność tę można przedstawić w postaci funkcji ,
Tutaj oznacza prędkość rakiety, mierzoną w częściach prędkości światła. Gdy na przykład poruszamy się z połową prędkości światła, to .
Wartości funkcji , oznaczają czas w sekundach, który upłynie dla obserwatora z Ziemi, gdy w rakiecie podróżnika upłynie jedna sekunda. Jeżeli obejrzymy wykres zależności dylatacji od , zauważymy coś dziwnego.
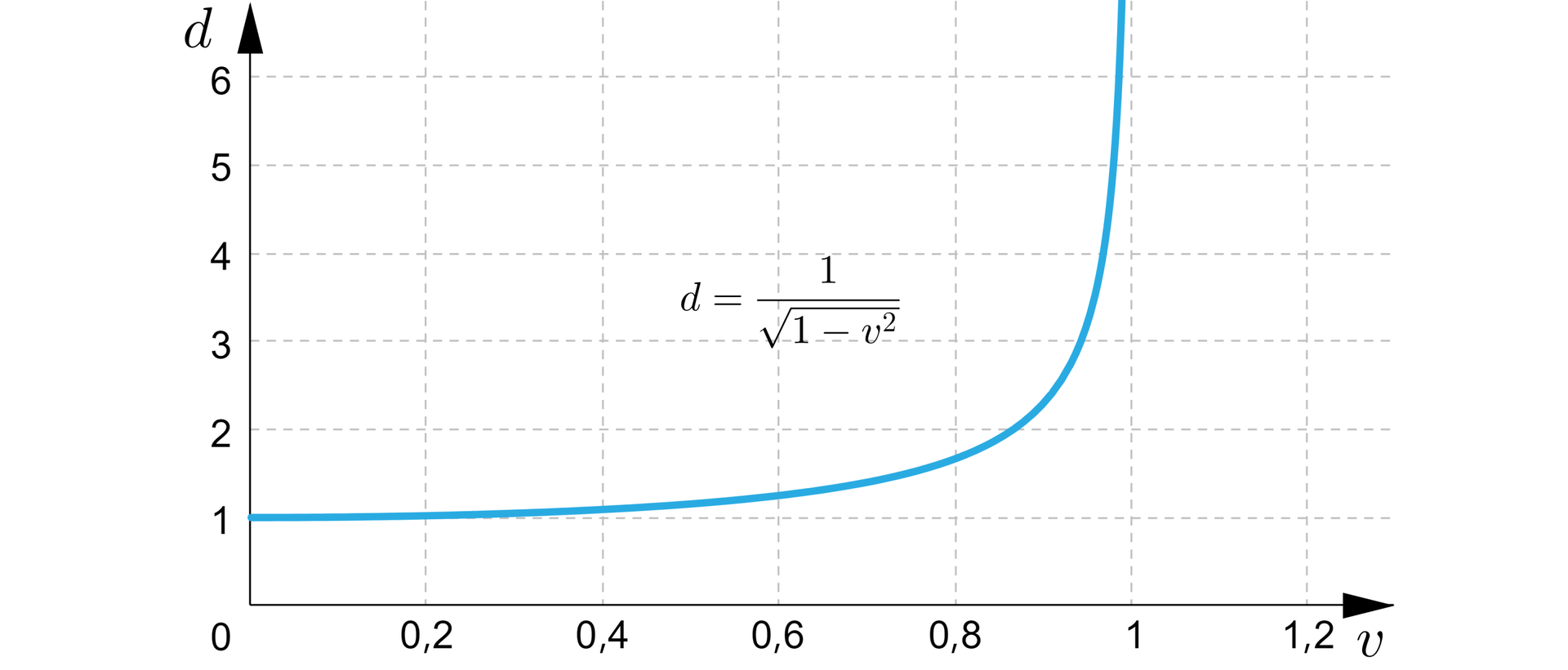
Gdy prędkości są małe, bliskie zera, wartość jest prawie równa jedności, czyli czas upływa w rakiecie i na Ziemi praktycznie tak samo. Gdy wartości prędkości są coraz bliższe jedynce, czyli prędkość rakiety zbliża się do prędkości światła, wartość dylatacji nie tylko rośnie gwałtownie, ale rośnie nieograniczenie! Zatem, gdyby rakieta pędziła z prędkością bliską prędkości światła, na przykład prędkości światła, to gdy w rakiecie upłynie sekunda, na Ziemi upłynie cały rok! Nie jesteśmy ponadto w stanie nigdy przekroczyć prędkości światła, gdyż wówczas czas w rakiecie musiałby płynąć nieskończenie wolno...
Granice niewłaściweGranice niewłaściwe występują wielokrotnie w fizyce, chociażby w zjawisku rezonansu – warto o tym przeczytać w wolnym czasie.
Definicja granicy niewłaściwej w punkcie
Podobnie, jak w przypadku granic właściwychgranic właściwych, granice niewłaściwe możemy zdefiniować na dwa równoważne sposoby, według Heinego i Cauchy’ego.
Mówimy, że funkcja ma w punkcie granicę niewłaściwą równą , gdy poza samym punktem pewne jego otoczenie należy do dziedziny tej funkcji oraz dla dowolnego ciągu argumentów z dziedziny, dążącego do , wartości dążą do .
Mówimy, że funkcja ma w punkcie granicę niewłaściwą równą , gdy poza samym punktem pewne jego otoczenie należy do dziedziny tej funkcji oraz dla dowolnie dużej wartości dodatniej liczby istnieje taka liczba dodatnia , że dla wszystkich argumentów z dziedziny pomiędzy i wartości są większe od .
Symbolicznie zapisujemy to jako
Podobnie definiujemy granicę niewłaściwą równą .
Sprawdzimy, używając definicji Heinego, czy funkcja , , ma w punkcie granicę niewłaściwą.
Rozwiązanie
Weźmy dowolny ciąg argumentów dążący do zera. Wówczas wiemy, że ciąg kwadratów tych argumentów, , również dąży do zera, przyjmując tylko wartości dodatnie. Zatem ciąg odwrotności kwadratów, , dąży do , czyli granicą funkcji w punkcie jest :
.
Sprawdzimy, używając definicji Cauchy’ego, czy funkcja , , ma w punkcie granicę niewłaściwągranicę niewłaściwą.
Rozwiązanie
Weźmy dowolnie dużą liczbę dodatnią . Jeżeli zdefiniujemy liczbę dodatnią równą odwrotności pierwiastka z , czyli , to wówczas dla wszystkich niezerowych wartości większych od i mniejszych od wartości funkcji są większe od i tym samym granicą funkcji w punkcie jest .
Możemy sprawdzić empirycznie, jak wygląda znajdowanie wartości w zależności od wartości .
Należy pamiętać, że im większa wartość , tym mniejsza jest wartość – węższy jest zakres argumentów, dla których wartości funkcji są powyżej zadanej linii – ale za każdym razem można taką wartość znaleźć.
Wyznaczymy granicę funkcji w punkcie .
Rozwiązanie
Skorzystamy z definicji Heinego. Weźmy dowolny ciąg argumentów dążący do zera. Wówczas:
.
Wyznaczymy granicę funkcji w punkcie .
Rozwiązanie
Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów dążących do . Wówczas:
Na koniec rozważań pokażemy przykłady funkcji, które nie mają granicy w punkcie.
Zbadamy, czy funkcja ma granicę dla .
Rozwiązanie
Narysujemy wykres funkcji :
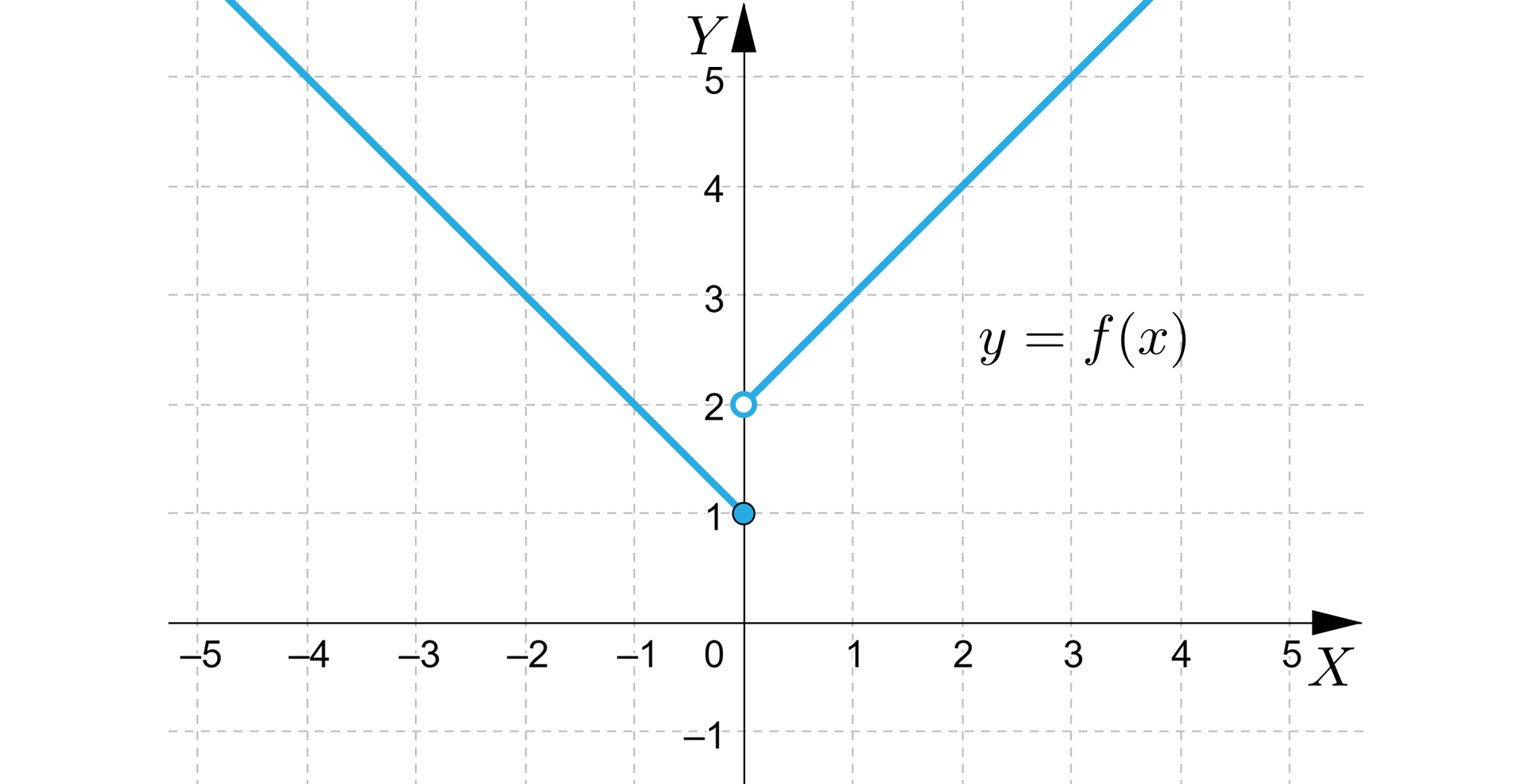
Łatwo zobaczyć, że granica w zerze z lewej strony jest równa , zaś z prawej strony jest równa , tym samym nie istnieje granica tej funkcji w punkcie , ani skończona, ani nieskończona.
Zbadamy istnienie granicy funkcji , w punkcie .
Rozwiązanie
Przyjrzyjmy się wykresowi funkcji :
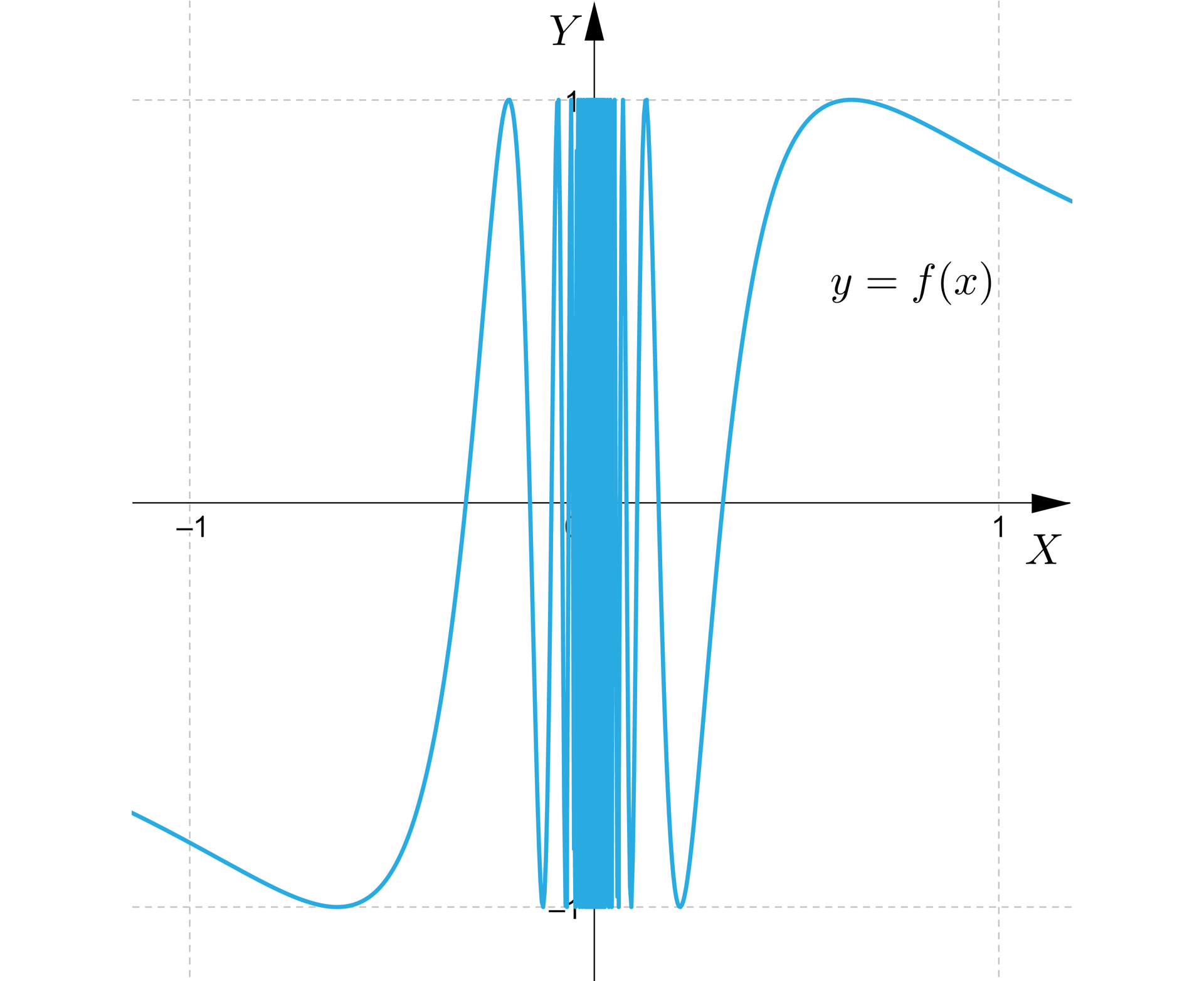
Gdy wartości zbliżają się do zera – na przykład z prawej strony – to wartości są coraz większe i sinus tych argumentów oscyluje coraz szybciej pomiędzy i . Taka funkcja w ogóle nie ma granicy, nawet nie posiada granic jednostronnych.
Rozważmy dwa ciągi zbieżne do : oraz .
Wówczas:
oraz
To dowodzi, że granica , w punkcie nie istnieje.
Słownik
granica funkcji w punkcie, która jest liczbą rzeczywistą
granica funkcji w punkcie, która jest nieskończona ( lub )