Przeczytaj

Przypomnijmy definicje i twierdzenia, z których będziemy korzystać podczas rozwiazywania układów równań postaci $\{\begin{cases} y = a x^{2} + b x + c \\ y = d x + e \end{cases}$ .

Układ równań

Definicja: Układ równań

Układem równań nazywamy koniunkcję co najmniej dwóch równań.

Aby rozwiązać układ równań należy znaleźć wszystkie układy liczb spełniające jednocześnie wszystkie równania składowe danego układu równań.

Rozwiązanie układu równań

Definicja: Rozwiązanie układu równań

Rozwiązaniem układu równań nazywamy każdą parę liczb spełniających jednocześnie każde równanie danego układu równań.

Równanie kwadratowe z jedną niewiadomą

Definicja: Równanie kwadratowe z jedną niewiadomą

Równaniem kwadratowym z jedną niewiadomą $x$ , nazywamy równanie postaci

a x^{2} + b x + c = 0

gdzie:
$a$ , $b$ i $c$ są dowolnymi liczbami rzeczywistymi oraz $a \neq 0$ .

Wyróżnik trójmianu kwadratowego („delta”)

Definicja: Wyróżnik trójmianu kwadratowego („delta”)

Wyróżnikiem trójmianu kwadratowego $a x^{2} + b x + c$ nazywamy wyrażenie postaci

∆ = b^{2} - 4 a c

W zależności od wartości trójmianu kwadratowego, równanie kwadratowerównanie kwadratowe może mieć dwa lub jeden pierwiastek. Może też nie posiadać rozwiązania.

Liczba rozwiązań równania kwadratowego

Twierdzenie: Liczba rozwiązań równania kwadratowego

Równanie kwadratowe postaci $a x^{2} + b x + c = 0$ , $a \neq 0$ :

nie posiada rozwiązania, jeśli $∆ < 0$ ;

posiada jedno rozwiązanie $x_{0} = \frac{- b}{2 a}$ , jeśli $∆ = 0$ ;

posiada dwa rozwiązania $x_{1} = \frac{- b - \sqrt{∆}}{2 a}$ oraz $x_{2} = \frac{- b + \sqrt{∆}}{2 a}$ , jeśli $∆ > 0$ .

Układy równań drugiego stopnia

Definicja: Układy równań drugiego stopnia

Układem równań drugiego stopnia, nazywamy takie układy, w których jedno równanie jest drugiego stopnia, a stopień drugiego nie jest większy niż dwa.

Rozwiążemy teraz kilka układów równań postaci $\{\begin{cases} y = a x^{2} + b x + c \\ y = d x + e \end{cases}$ .

Przykład 1

Rozwiążemy układ równań $\{\begin{cases} y = 5 x^{2} - 3 x - 8 \\ y = 2 - 8 x \end{cases}$ .

Podstawiamy wyrażenie wyznaczone w równaniu liniowym, do równania kwadratowego w miejsce niewiadomej $y$ .

$\{\begin{cases} 2 - 8 x = 5 x^{2} - 3 x - 8 \\ y = 2 - 8 x \end{cases}$

Porządkujemy otrzymane równanie kwadratowe.

$5 x^{2} + 5 x - 10 = 0 | : 5$

$x^{2} + x - 2 = 0$

Następnie rozwiązujemy je, obliczając na wyróżnik trójmianu kwadratowegowyróżnik trójmianu kwadratowegowyróżnik trójmianu kwadratowego równania $a x^{2} + b x + c = 0$ oraz jego pierwiastki.

$∆ = b^{2} - 4 a c$

$∆ = 1^{2} - 4 \cdot 1 \cdot (- 2)$

$∆ = 9 > 0$

$\sqrt{∆} = 3$

$x_{1} = \frac{- b - \sqrt{∆}}{2 a}$ lub $x_{2} = \frac{- b + \sqrt{∆}}{2 a}$

$x_{1} = \frac{- 1 - 3}{2} = - 2$ lub $x_{2} = \frac{- 1 + 3}{2} = 1$

Podstawiamy otrzymane wartości niewiadomej $x$ do równania liniowego i obliczmy niewiadomą $y$ .

$\{\begin{cases} x = - 2 \\ y = 2 - 8 x \end{cases}$ lub $\{\begin{cases} x = 1 \\ y = 2 - 8 x \end{cases}$

$\{\begin{cases} x = - 2 \\ y = 18 \end{cases}$ lub $\{\begin{cases} x = 1 \\ y = - 6 \end{cases}$

A zatem rozwiązaniem tego układu równań są dwie pary liczb $\{\begin{cases} x = - 2 \\ y = 18 \end{cases}$ oraz $\{\begin{cases} x = 1 \\ y = - 6 \end{cases}$ .

Przykład 2

Rozwiążemy układ równań $\{\begin{cases} - 2 (2 - 2 \sqrt{2}) x + y = 10 + x^{2} \\ 4 x - y = - 2 \end{cases}$ .

Doprowadzamy równania występujące w układzie do najprostszej postaci i wyznaczamy w równaniach niewiadomą $y$ .

$\{\begin{cases} y = x^{2} + 2 (2 - 2 \sqrt{2}) x + 10 \\ - y = - 4 x - 2 | : (- 1) \end{cases}$

$\{\begin{cases} y = x^{2} + 2 (2 - 2 \sqrt{2}) x + 10 \\ y = 4 x + 2 \end{cases}$

Wyznaczoną w równaniu liniowym wartość $y$ , podstawiamymetoda podstawianiapodstawiamy do równania kwadratowego.

$\{\begin{cases} 4 x + 2 = x^{2} + 2 (2 - 2 \sqrt{2}) x + 10 \\ y = 4 x + 2 \end{cases}$

W pierwszym równaniu otrzymaliśmy równanie kwadratowe – porządkujemy je.

$x^{2} + 2 (2 - 2 \sqrt{2}) x - 4 x - 2 + 10 = 0$

$x^{2} + 4 x - 4 \sqrt{2} x - 4 x - 2 + 10 = 0$

$x^{2} - 4 \sqrt{2} x + 8 = 0$

Rozwiązujemy otrzymane równanie.

$∆ = b^{2} - 4 a c$

$∆ = {(4 \sqrt{2})}^{2} - 4 \cdot 1 \cdot 8$

$∆ = 32 - 32$

$∆ = 0$

A wtedy

$x_{0} = \frac{- b}{2 a}$

$x_{0} = \frac{4 \sqrt{2}}{2}$

$x_{0} = 2 \sqrt{2}$

Podstawiamy otrzymaną wartość niewiadomej $x$ do równania liniowego i obliczmy niewiadomą $y$ .

$\{\begin{cases} x = 2 \sqrt{2} \\ y = 4 x + 2 \end{cases}$

$\{\begin{cases} x = 2 \sqrt{2} \\ y = 4 \cdot 2 \sqrt{2} + 2 \end{cases}$

Rozwiązaniem tego układu równań jest jedna para liczb $\{\begin{cases} x = 2 \sqrt{2} \\ y = 2 + 8 \sqrt{2} \end{cases}$ .

Przykład 3

Rozwiążemy układ równańukład równańukład równań $\{\begin{cases} 4 (x - x^{2}) - 15 = 10 - y \\ 15 x - y = 5 \end{cases}$ .

Doprowadzamy równania występujące w układzie do najprostszej postaci i wyznaczamy w równaniach niewiadomą $y$ .

$\{\begin{cases} 4 x - 4 x^{2} - 15 = 10 - y \\ 15 x - y = 5 \end{cases}$

$\{\begin{cases} y = 4 x^{2} - 4 x + 15 + 10 \\ - y = 5 - 15 x \end{cases}$

$\{\begin{cases} y = 4 x^{2} - 4 x + 25 \\ y = 15 x - 5 \end{cases}$

Wyznaczoną w równaniu liniowym wartość $y$ , podstawiamy do równania kwadratowego, które następnie porządkujemy.

$\{\begin{cases} 15 x - 5 = 4 x^{2} - 4 x + 25 \\ y = 15 x - 5 \end{cases}$

$\{\begin{cases} 4 x^{2} - 4 x - 15 x + 5 + 25 = 0 \\ y = 15 x - 5 \end{cases}$

$\{\begin{cases} 4 x^{2} - 19 x + 30 = 0 \\ y = 15 x - 5 \end{cases}$

Rozwiązujemy otrzymane równanie kwadratowe.

Obliczamy wartość wyróżnika trójmianu kwadratowego.

$∆ = 19^{2} - 4 \cdot 4 \cdot 30 = - 119 < 0$

$∆ < 0$ , a więc równanie kwadratowe $4 x^{2} - 19 x + 30 = 0$ nie posiada rozwiązania.

Zatem układ równań $\{\begin{cases} 4 (x - x^{2}) - 15 = 10 - y \\ 15 x - y = 5 \end{cases}$ jest sprzeczny.

Liczba rozwiązań układu równań $\{\begin{cases} y = a x^{2} + b x + c \\ y = d x + e \end{cases}$ jest taka sama, jak liczba rozwiązań otrzymanego z porównania prawych stron równań składowych tego układu, równania kwadratowego.

Przykład 4

Określimy liczbę rozwiązań układu równań $\{\begin{cases} 3 x^{2} + x + m = y - 2 m \\ y - m x = 5 m + 2 \end{cases}$ z niewiadomą $x$ , w zależności od wartości parametru $m$ .

W równaniach wyznaczamy zmienną $y$ .

$\{\begin{cases} y = 3 x^{2} + x + m + 2 m \\ y = m x + 5 m + 2 \end{cases}$

$\{\begin{cases} y = 3 x^{2} + x + 3 m \\ y = m x + 5 m + 2 \end{cases}$

Podstawiamy do równania kwadratowego wyrażenie, otrzymane w równaniu liniowym.

$\{\begin{cases} m x + 5 m + 2 = 3 x^{2} + x + 3 m \\ y = m x + 5 m + 2 \end{cases}$

$\{\begin{cases} 3 x^{2} + x - m x + 3 m - 5 m - 2 = 0 \\ y = m x + 5 m + 2 \end{cases}$

$\{\begin{cases} 3 x^{2} + (1 - m) x - 2 (m + 1) = 0 \\ y = m x + 5 m + 2 \end{cases}$

Otrzymujemy równanie kwadratowe z niewiadomą $x$ i parametrem $m$ .

$3 x^{2} + (1 - m) x - 2 (m + 1) = 0$

Wyznaczamy wartość wyróżnika trójmianu kwadratowego.

$∆ = {(1 - m)}^{2} - 4 \cdot 3 \cdot (- 2 (m + 1))$

$∆ = m^{2} - 2 m + 1 + 24 m + 24$

$∆ = m^{2} + 22 m + 25$

Zgodnie z przypomnianym na początku materiału twierdzeniem, liczba pierwiastków równania kwadratowego jest zależna od wartości wyróżnika kwadratowego (delty).

Sprawdzimy zatem, dla jakich wartości parametru $m$ , delta przyjmuje wartości dodatnie, a dla jakich ujemne.

$∆_{m} = 22^{2} - 4 \cdot 1 \cdot 25$

$∆_{m} = 384$

$\sqrt{∆_{m}} = 8 \sqrt{6}$

$m_{1} = \frac{- 22 - 8 \sqrt{6}}{2} = - 11 - 4 \sqrt{6}$

$m_{2} = \frac{- 22 + 8 \sqrt{6}}{2} = - 11 + 4 \sqrt{6}$

R1KRrkkp3TLBs

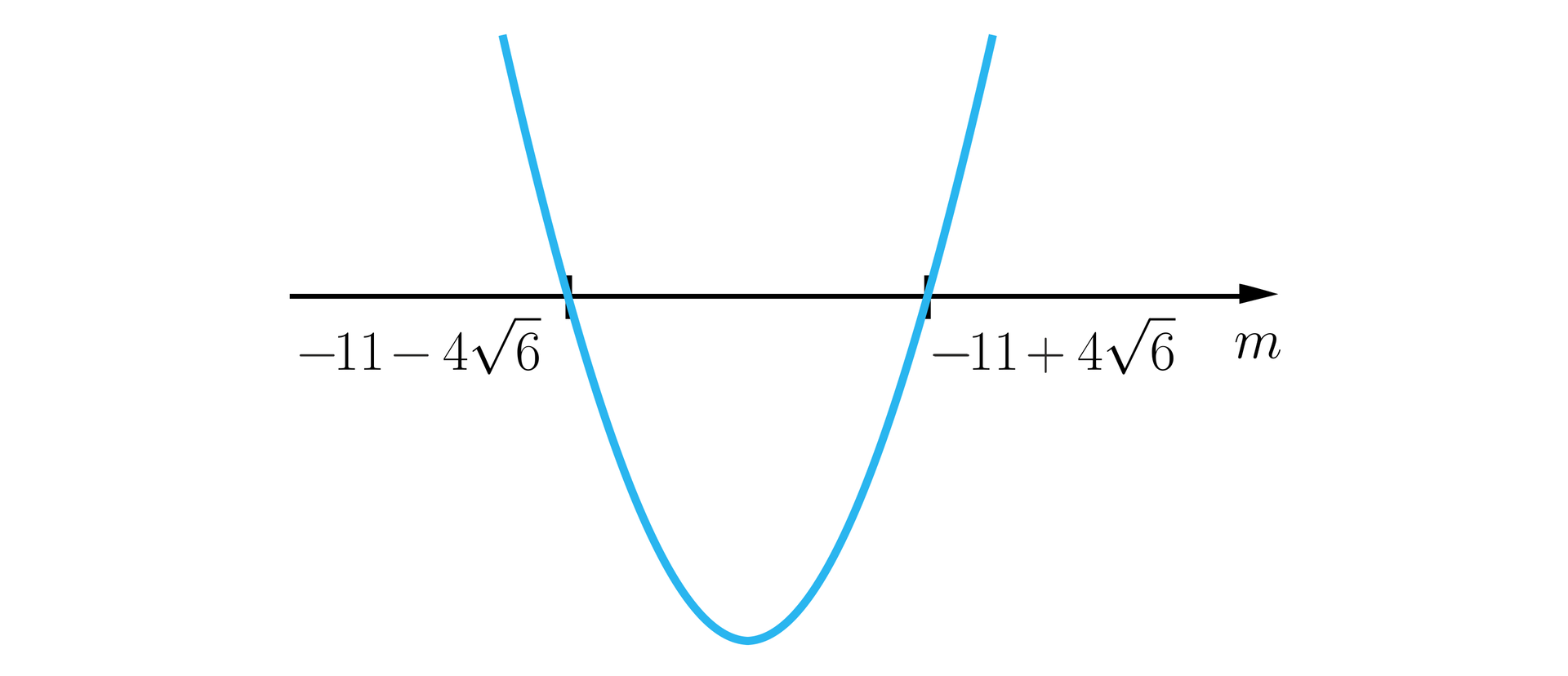
Ilustracja przedstawia poziomą oś m, którą przecina parabola o ramionach skierowanych do góry i miejscach zerowych kolejno w punkcie -11-46, i -11+46.

Mamy więc:

jeden pierwiastek $\Leftrightarrow ∆ = 0 \Leftrightarrow m \in \{- 11 - 4 \sqrt{6}, - 11 + 4 \sqrt{6}\}$ ;

dwa pierwiastki $\Leftrightarrow ∆ > 0 \Leftrightarrow m \in (- \infty, - 11 - 4 \sqrt{6}) \cup (- 11 + 4 \sqrt{6}, \infty)$ ;

brak pierwiastków $\Leftrightarrow ∆ < 0 \Leftrightarrow m \in (- 11 - 4 \sqrt{6}, - 11 + 4 \sqrt{6})$ .

Liczba rozwiązań układu równań $\{\begin{cases} 3 x^{2} + x + m = y - 2 m \\ y - m x = 5 m + 2 \end{cases}$ jest taka sama, jak liczba pierwiastków równania

$3 x^{2} + (1 - m) x - 2 (m + 1) = 0$

A zatem:

dla $m \in (- \infty, - 11 - 4 \sqrt{6}) \cup (- 11 + 4 \sqrt{6}, \infty)$ rozwiązaniem układu równań $\{\begin{cases} 3 x^{2} + x + m = y - 2 m \\ y - m x = 5 m + 2 \end{cases}$ są dwie pary liczb;

dla $m \in \{- 11 - 4 \sqrt{6}, - 11 + 4 \sqrt{6}\}$ rozwiązaniem układu równań $\{\begin{cases} 3 x^{2} + x + m = y - 2 m \\ y - m x = 5 m + 2 \end{cases}$ jest jedna para liczb;

dla $m \in (- 11 - 4 \sqrt{6}, - 11 + 4 \sqrt{6})$ układ równań $\{\begin{cases} 3 x^{2} + x + m = y - 2 m \\ y - m x = 5 m + 2 \end{cases}$ nie posiada rozwiązań.

Przykład 5

Określimy, dla jakiego parametru $m \in ℝ ∖ \{- 1\}$ , rozwiązaniem układu równań $\{\begin{cases} y = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$ są dwie pary liczb.

Wyznaczone w równaniu liniowym wyrażenie podstawiamy do równania kwadratowego w miejsce niewiadomej $y$ .

$\{\begin{cases} y = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$

$\{\begin{cases} - m (1 + x) = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$

Rozwiązaniem układu równań $\{\begin{cases} y = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$ będą dokładnie dwie pary liczb, wtedy, gdy równanie $- m (1 + x) = x^{2} (1 + m) + m x - 1$ będzie miało dwa różne pierwiastki.

Porządkujemy je i obliczamy wartość wyróżnika trójmianu kwadratowego.

$- m (1 + x) = x^{2} (1 + m) + m x - 1$

$- m - m x = x^{2} + m x^{2} + m x - 1$

$(1 + m) x^{2} + m x + m x + m - 1 = 0$

$(1 + m) x^{2} + 2 m x + (m - 1) = 0$

$∆ = {(2 m)}^{2} - 4 \cdot (m + 1) (m - 1)$

$∆ = 4 m^{2} - 4 m^{2} + 4$

$∆ = 4$

A zatem równanie kwadratowe $(1 + m) x^{2} + 2 m x + (m - 1) = 0$ posiada dwa różne rozwiązania dla każdego $m \in ℝ ∖ \{- 1\}$ .

Stąd wynika, że dla każdego $m \in ℝ ∖ \{- 1\}$ rozwiązaniem układu równań $\{\begin{cases} y = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$ są dwie pary liczb.

Wyznaczymy te rozwiązania.

$x_{1} = \frac{- 2 m - 2}{2 (m + 1)} = \frac{- 2 (m + 1)}{2 (m + 1)} = - 1$ lub $x_{2} = \frac{- 2 m + 2}{2 (m + 1)} = \frac{- 2 (m - 1)}{2 (m + 1)} = \frac{1 - m}{m + 1}$

Podstawiamy otrzymane wartości $x$ do układu równań i wyznaczamy niewiadomą $y$ .

$\{\begin{cases} x = - 1 \\ y = - m (1 + x) \end{cases}$ lub $\{\begin{cases} x = \frac{- 1 (m - 1)}{m + 1} \\ y = - m (1 + x) \end{cases}$

${\begin{cases} x = - 1 \\ y = 0 \end{cases}$ lub $\{\begin{cases} x = \frac{- 1 (m - 1)}{m + 1} \\ y = \frac{- m (2 - 0)}{m + 1} \end{cases}$

A zatem dla dowolnego $m \in ℝ ∖ \{- 1\}$ układ równań $\{\begin{cases} y = x^{2} (1 + m) + m x - 1 \\ y = - m (1 + x) \end{cases}$ posiada dwa rozwiązania postaci $\{\begin{cases} x = - 1 \\ y = 0 \end{cases}$ lub $\{\begin{cases} x = \frac{1 - m}{m + 1} \\ y = \frac{- 2 m}{m + 1} \end{cases}$ .

Słownik

układ równań

koniunkcja co najmniej dwóch równań

równanie kwadratowe z jedną niewiadomą

równanie z niewiadomą $x$ postaci

a x^{2} + b x + c = 0

gdzie:
$a$ , $b$ i $c$ są dowolnymi liczbami rzeczywistymi oraz $a \neq 0$

metoda podstawiania

metoda polegająca na wyznaczeniu dowolnej niewiadomej z dowolnego równania i podstawieniu tak uzyskanego wyrażenia do drugiego z równań w miejsce wyznaczonej niewiadomej

wyróżnik trójmianu kwadratowego

∆ = b^{2} - 4 a c

Wprowadzenie

Schemat interaktywny

Słownik