Sześcian jest wpisany w kulę, jeśli wszystkie wierzchołki sześcianu leżą na powierzchni kuli.

Rozważmy sześcian o krawędzi długości $6 \mathrm{cm}$. Jaką objętość będzie miała kula opisana na tym sześcianie?

Rozwiązanie:

Do rozwiązania tego problemu wykorzystamy przekrój płaszczyzną zawierającą przekątną sześcianu i przekątną podstawy sześcianu.

R1Z9wOS26q97d

Ilustracja przedstawia okrąg opisany na prostokącie o krótszym boku długości a oraz dłuższym boku długości a pierwiastków z dwóch. Zaznaczono przekątną tego prostokąta, której środek stanowi punkt S. Połowa długości przekątnej równa się promieniowi okręgu opisanego na tym czworokącie.

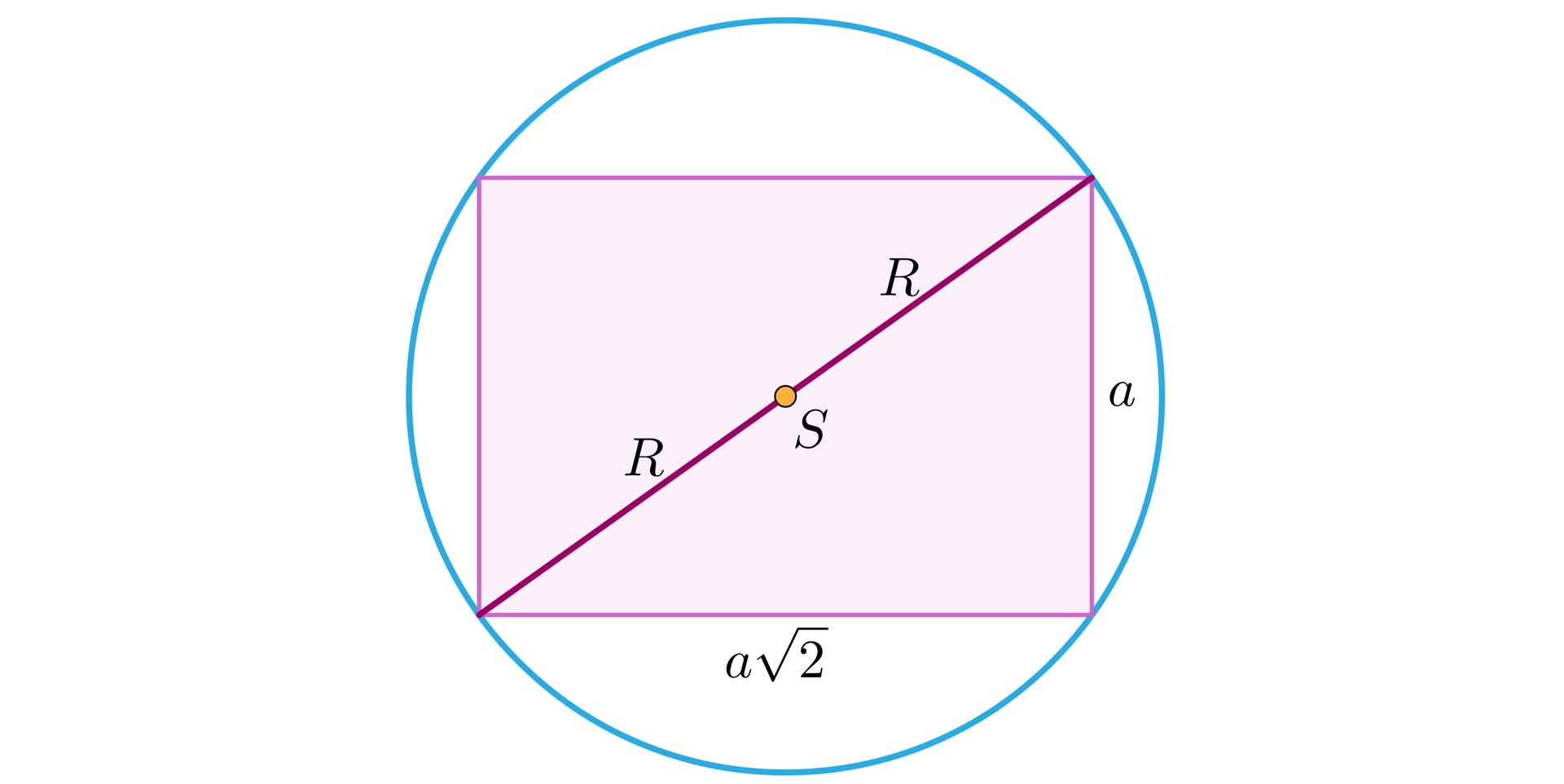
Krawędź sześcianu $a=6 \mathrm{cm}$. Promień kuli $R$ stanowi połowę długości przekątnej sześcianu, czyli $R=\frac{1}{2}a\sqrt{3}=3\sqrt{3} \mathrm{cm}$.

A zatem $V=\frac{4}{3}\pi R^3=\frac{4}{3}·81\sqrt{3}\pi =108\sqrt{3}\pi {\mathrm{cm}}^3$.

Rozważmy kulę o objętości $36\pi$. Jaka będzie długość krawędzi sześcianu wpisanego w tą kulę?

Rozwiązanie:

Do rozwiązania tego problemu wykorzystamy przekrójprzekrójprzekrój płaszczyzną zawierającą przekątną sześcianu i przekątną podstawy sześcianu.

R521FxP0Vn91L

Ilustracja przedstawia okrąg opisany na prostokącie o krótszym boku długości a oraz dłuższym boku długości a pierwiastków z dwóch. Zaznaczono przekątną tego prostokąta, której środek stanowi punkt S. Połowa długości przekątnej równa się promieniowi okręgu opisanego na tym czworokącie.

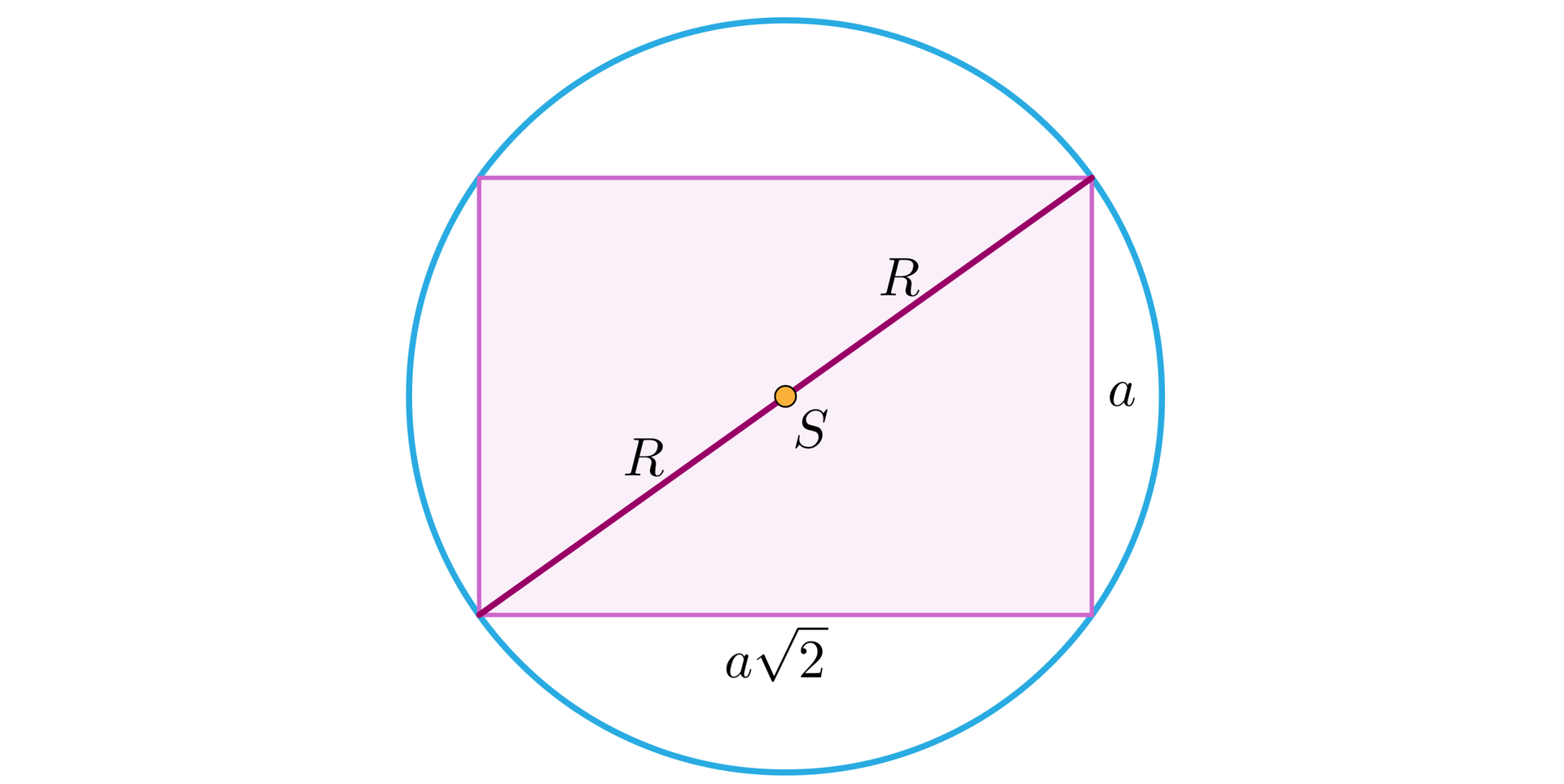
Mając daną objętość kuli możemy obliczyć długość jej promienia. Wystarczy podstawić do wzoru $V=\frac{4}{3}\pi R^3$.

Otrzymujemy równanie:

$\frac{4}{3}\pi R^3=36\pi$

$\frac{4}{3}{R}^3=36$

$R^3=27$

$R=3$.

Długość krawędzi sześcianu możemy teraz obliczyć na dwa sposoby:

$\mathrm{I}$. Korzystając z twierdzenia Pitagorasa. Otrzymujemy wówczas równanie:

$a^2+{\left(a\sqrt{2}\right)}^2=\left(2R\right){}^2$

$3a^2=36$

$a^2=12$

$a=2\sqrt{3}$

$\mathrm{II}$. Korzystając ze wzoru na przekątną sześcianu. Otrzymujemy wówczas równanie:

$a\sqrt{3}=2R$

$a\sqrt{3}=6$

$a=\frac{6}{\sqrt{3}}=2\sqrt{3}$

Jaki procent objętości kuli stanowi objętość sześcianu wpisanego w tę kulę? Przyjmijmy przybliżenie $\pi \approx 3,14$.

Rozwiązanie:

Przyjmijmy, że krawędź sześcianu ma długość $a$.

Zatem objętość tego sześcianu $V_s=a^3$.

Promień kuli na tym sześcianie $R=\frac{1}{2}a\sqrt{3}$.

Zatem objętość kuli $V_k=\frac{4}{3}\pi {\left(\frac{1}{2}a\sqrt{3}\right)}^3=\frac{4}{3}·\frac{1}{8}·3\sqrt{3}·\pi a^3=\frac{\sqrt{3}}{2}\pi a^3$.

Obliczamy stosunek objętości sześcianu do objętości kuli i wyrażamy go w procentach:

$x=\frac{a^3}{\frac{\sqrt{3}}{2}\pi a^3}\cdot 100\mathrm{\%}=\frac{2\sqrt{3}}{3\pi }\cdot 100\mathrm{\%}\approx \frac{2\cdot 1,73}{3\cdot 3,14}\cdot 100\mathrm{\%}\approx 36,73\mathrm{\%}$.

Czy kulę o powierzchni $48\pi {\mathrm{cm}}^2$ można opisać na sześcianie o objętości $64{\mathrm{c}\mathrm{m}}^3$? Odpowiedź uzasadnimy rachunkowo.

Rozwiązanie:

Wykonajmy odpowiedni rysunek. Będzie to przekrój sześcianu płaszczyzną przechodzącą przez środek kuli i przekątną podstawy sześcianu.

R3pJACmeYNwAt

Ilustracja przedstawia okrąg opisany na prostokącie o krótszym boku długości a oraz dłuższym boku długości a pierwiastków z dwóch. Zaznaczono przekątną tego prostokąta, której środek stanowi punkt S. Połowa długości przekątnej równa się promieniowi okręgu opisanego na tym czworokącie.

Nasze zadanie to porównanie dwóch wartości: średnicy kuli i przekątnej sześcianu.

Aby obliczyć promień kuli rozwiązujemy równanie wykorzystując dane w zadaniu:

$4\pi R^2=48\pi$

$R^2=12$

$R=2\sqrt{3}$

czyli $2R=4\sqrt{3}$.

Do obliczenia długości krawędzi sześcianu wykorzystamy wzór na objętość sześcianu o krawędzi a.

$a^3=64$

$a=4$

Zatem przekątna sześcianu ma długość

$a\sqrt{3}=4\sqrt{3}$

Wynika stąd, że przekątna sześcianu jest równa średnicy kuli, czyli kulę o powierzchni $48\pi {\mathrm{cm}}^2$ można opisać na sześcianie o objętości $64 {\mathrm{cm}}^3$.

figura płaska powstająca w miejscu przecięcia bryły geometrycznej pewną płaszczyzną