Przeczytaj
Przypomnijmy definicję stożka.
Stożkiem nazywamy bryłę obrotową, która powstaje przez obrót trójkąta prostokątnego wokół osi, zawierającej jedną z przyprostokątnych.
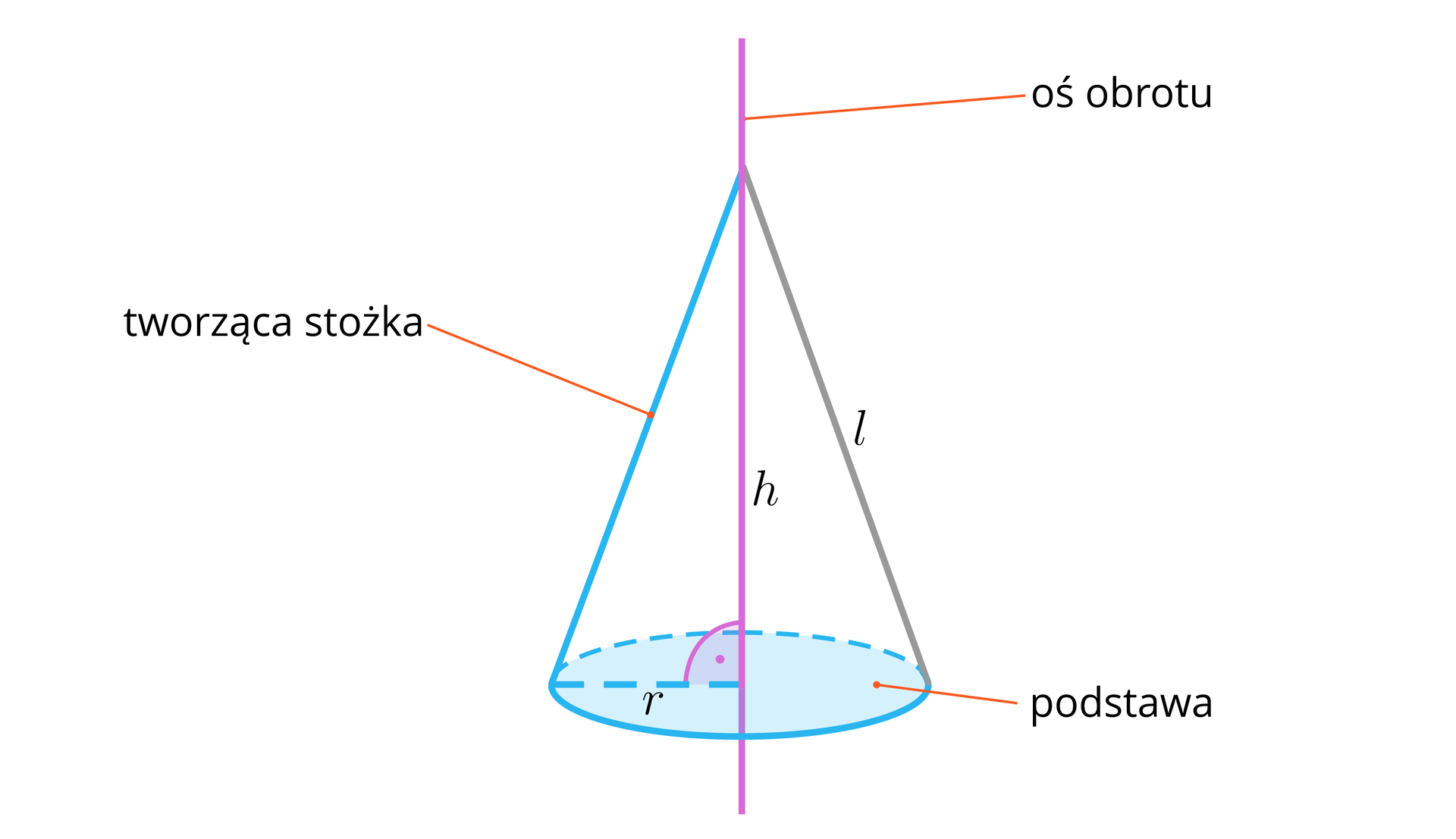
Przekrojem osiowym stożka nazywamy przekrój stożka płaszczyzną zawierającą jego oś obrotu. Jest nim trójkąt równoramienny utworzony ze średnicy podstawy stożka i dwóch tworzących.

Kąt pomiędzy ramionami przekroju osiowego (oznaczony na rysunku jako ) nazywamy kątem rozwarcia stożka.
W materiale omówimy, jak obliczyć pole powierzchni całkowitej stożka.
Pole powierzchni całkowitej stożka

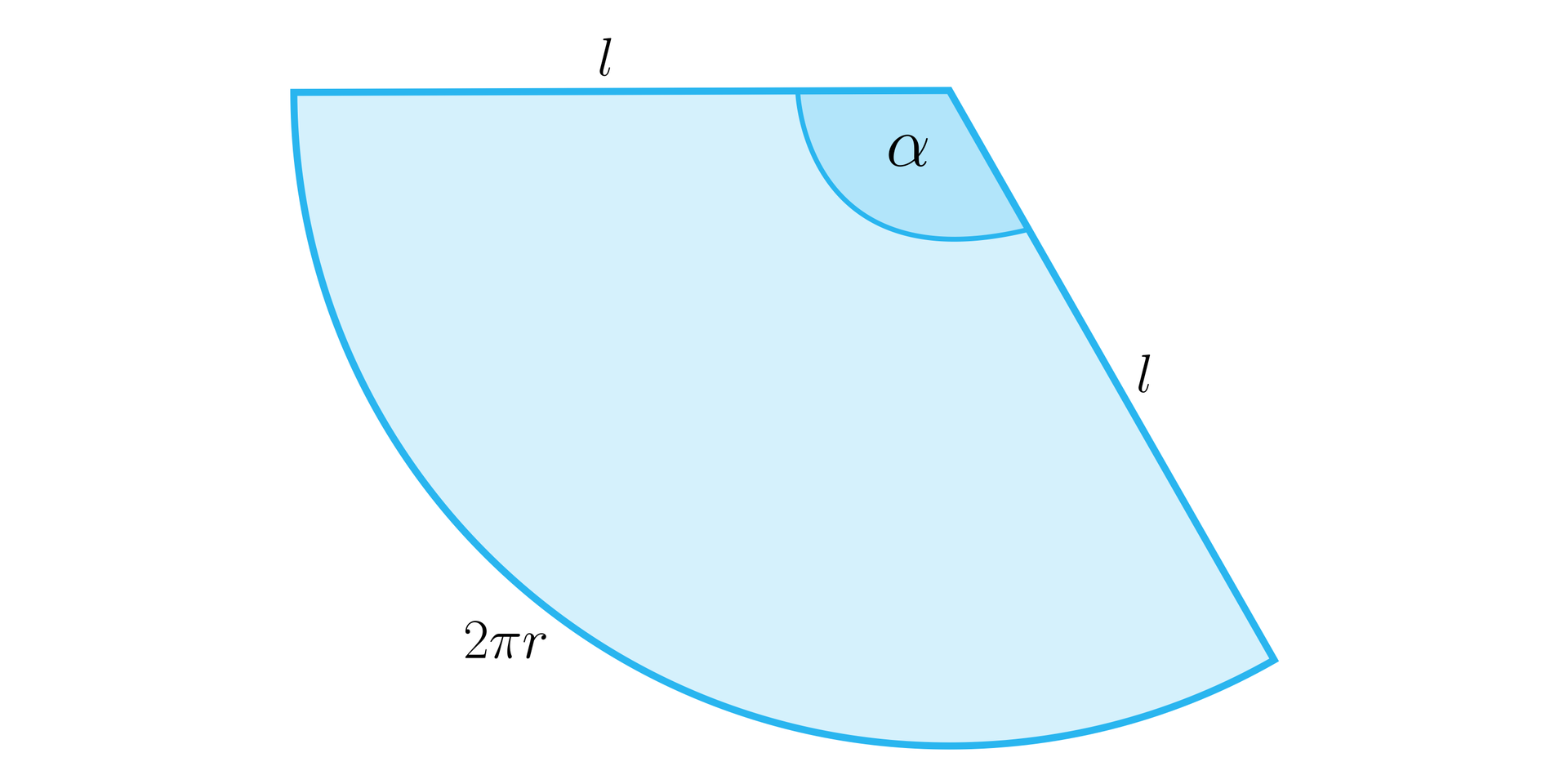
Zauważmy, że podstawa stożka jest kołem o promieniu , a powierzchnia boczna stożka jest wycinkiem koła o promieniu .
Pole powierzchni całkowitej stożka jest równe sumie pola powierzchni jego podstawy oraz powierzchni bocznej.
Zatem:
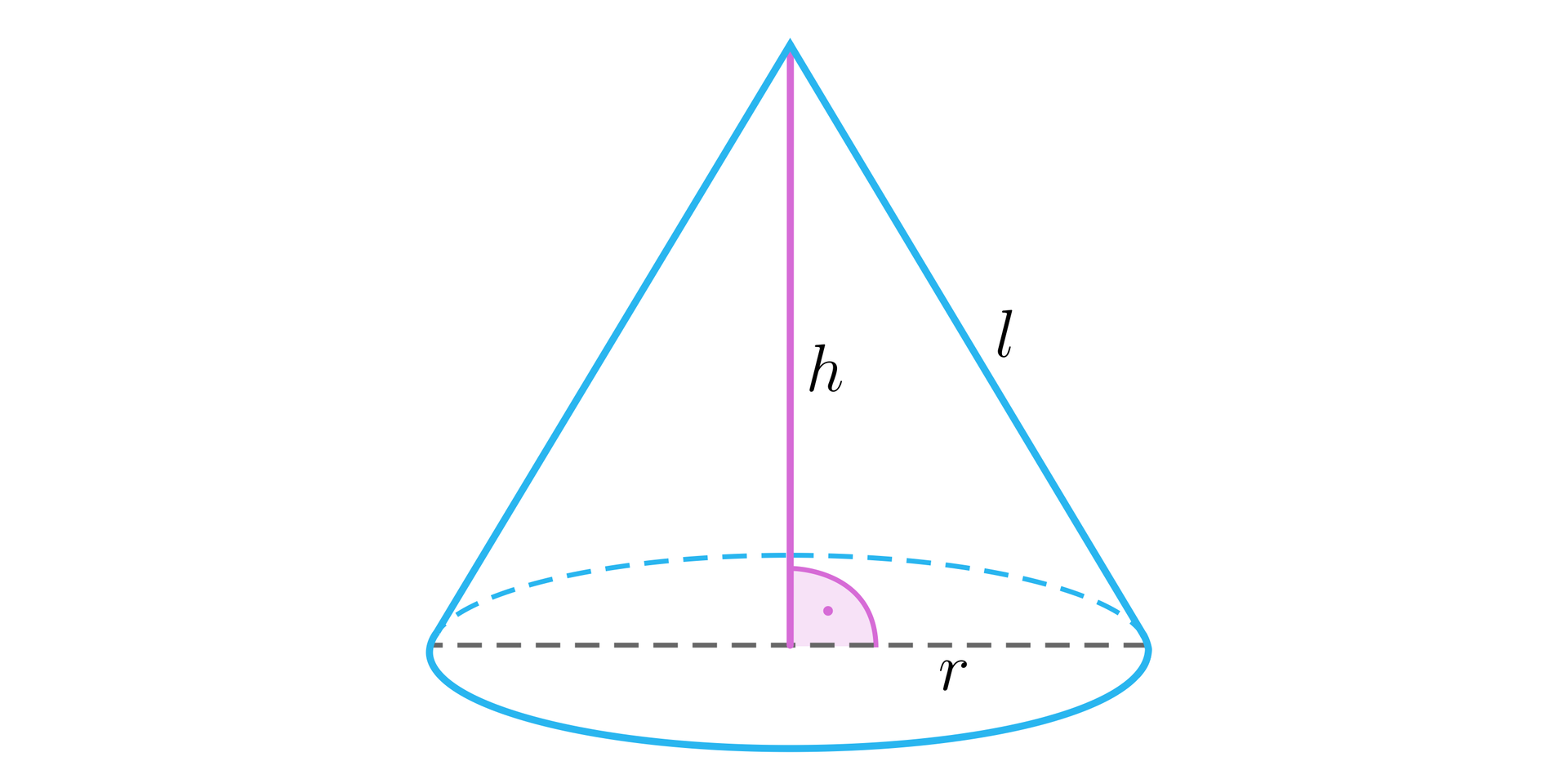
Jeżeli promień podstawy stożka ma długość , wysokość stożka , a tworząca ma długość , to:
Zauważmy, że po rozwinięciu powierzchnia boczna stożkapowierzchnia boczna stożka jest wycinkiem koła o promieniu , zatem jej pole możemy obliczyć ze wzoru:
Obliczymy pole powierzchnipole powierzchni całkowitej stożka z rysunku.
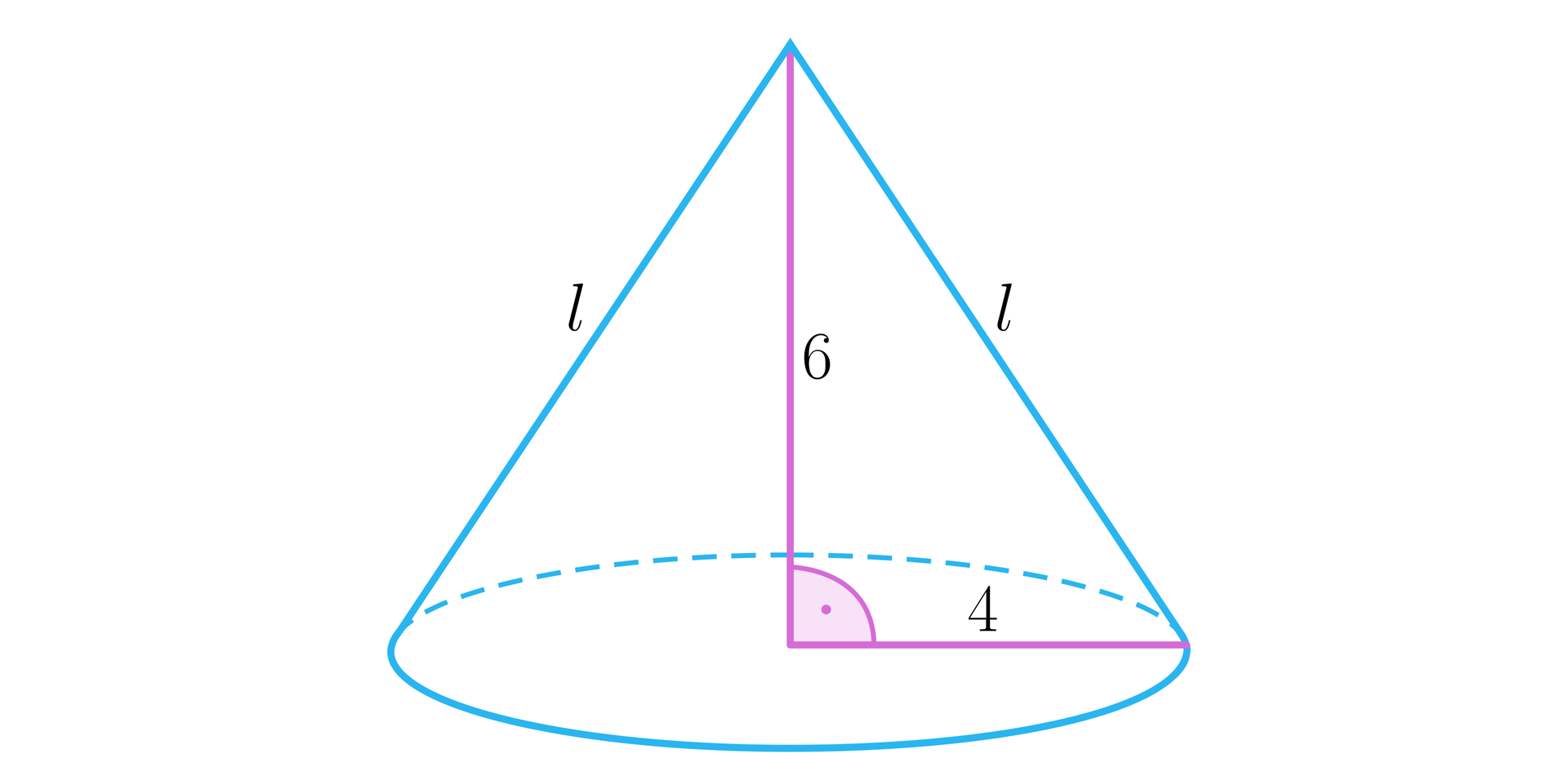
Rozwiązanie
Jeżeli przez oznaczymy długość promienia podstawy stożka, a przez długość wysokości stożka, to:
oraz .
Długość tworzącej stożka obliczamy z twierdzenia Pitagorasa:
, czyli .
Zatem .
Wobec tego pole powierzchni całkowitej stożka jest równe:
.
Wiadomo, że pole powierzchni podstawy stożka jest równe , a pole powierzchnipole powierzchni całkowitej wynosi . Obliczymy długość tworzącej w tym stożku.
Rozwiązanie
Narysujmy stożek i wprowadźmy oznaczenia, jak na rysunku.
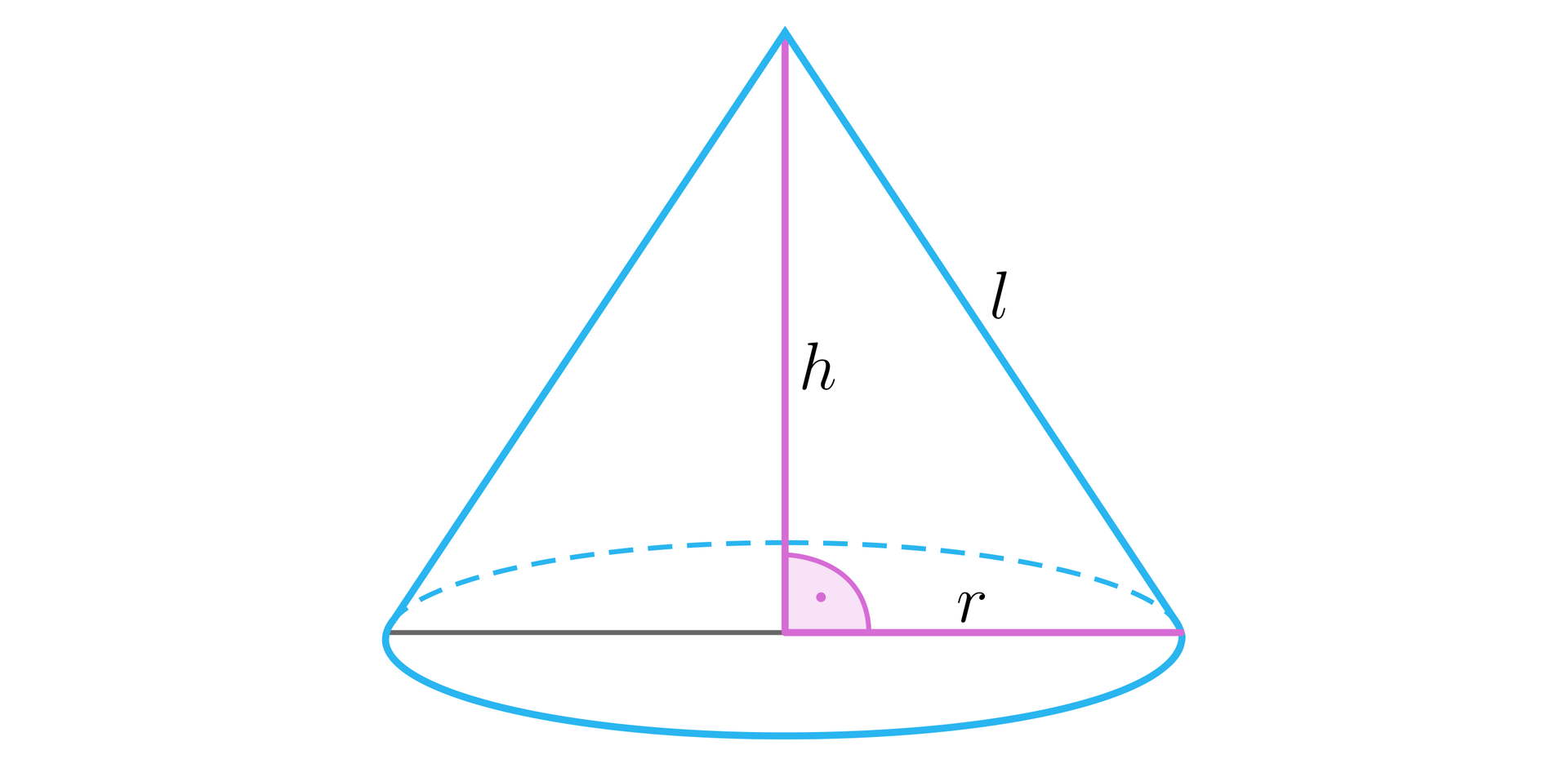
Ponieważ pole podstawy stożka wynosi , zatem do obliczenia długości promienia podstawy rozwiązujemy równanie:
.
Wobec tego .
Zauważmy, że pole powierzchni bocznej stożka obliczamy ze wzoru:
.
Ponieważ , zatem do wyznaczenia długości tworzącej stożka rozwiązujemy równanie:
, czyli .
Tworząca stożka ma długość .
Obliczymy pole powierzchni całkowitej stożka, w którym cosinus kąta rozwarcia wynosi , a tworząca stożka ma długość .
Rozwiązanie
Narysujmy stożek i wprowadźmy odpowiednie oznaczenia.

Z zadania wynika, że długość tworzącej oraz .
Do wyznaczenia długości promienia podstawy stożka wykorzystamy twierdzenie cosinusów.
Zatem
.
Pole powierzchni całkowitej tego stożka jest równe:
.
Długości promienia podstawy, wysokości oraz tworzącej stożka w pewnym stożku są w podanej kolejności wyrazami ciągu arytmetycznego o różnicy . Obliczymy pole powierzchni całkowitej tego stożka.
Rozwiązanie
Narysujmy stożek i wprowadźmy odpowiednie oznaczenia.

Ponieważ podstawa, wysokość oraz tworząca stożka tworzą trójkąt prostokątny, zatem do wyznaczenia wartości rozwiązujemy równanie:
Zatem .
Wobec tego długość tworzącej wynosi .
Pole powierzchni całkowitej tego stożka wynosi:
.
Przekrój osiowy stożka jest trójkątem równobocznym o polu . Wyznaczymy pole powierzchni całkowitej tego stożka.
Rozwiązanie
Narysujmy stożek i wprowadźmy odpowiednie oznaczenia:
Ponieważ przekrój osiowy stożka jest trójkątem równobocznym to .
Z faktu, że pole przekroju osiowego stożka wynosi wynika równanie:
, czyli .
Zatem .
Pole powierzchni całkowitej tego stożka wynosi:
.
Słownik
powierzchnia zakreślona przez przeciwprostokątną trójkąta prostokątnego podczas obrotu
miara przyporządkowująca powierzchni pewną nieujemną liczbę, która określa jej rozmiar