Przeczytaj

Wprowadźmy definicję i własności podobieństwapodobieństwopodobieństwa.

Podobieństwo

Definicja: Podobieństwo

Przekształcenie płaszczyzny na płaszczyznę, które zmienia odległość każdych dwóch punktów w pewnym stosunku nazywamy podobieństwem.

Podobieństwo o skali

k

Definicja: Podobieństwo o skali

k

Podobieństwem o skali $k > 0$ nazywamy takie przekształcenie $P$ płaszczyzny na tę samą płaszczyznę (mówimy wówczas o podobieństwie płaszczyzny) lub przestrzeni na tę samą przestrzeń (mówimy wówczas o podobieństwie przestrzeni), w którym

|A' B'| = k \cdot |A B|

gdzie:
$A$ i $B$ – są dwoma dowolnymi punktami,
$A'$ i $B'$ – obrazami tych punktów w przekształceniu $P$ .

Wobec tego definicję figur podobnych możemy sformułować następująco:

Figury podobne

Definicja: Figury podobne

Figury nazywamy podobnymi wtedy, gdy jedna z nich jest obrazem drugiej w pewnym podobieństwie. Relację podobieństwa figur oznaczamy symbolem „ $~$ ”. Fakt, że figura $F$ jest podobna do figury $G$ możemy zapisać następująco:

F ~ G

Skalę $k > 0$ tego podobieństwa nazywamy wtedy skalą podobieństwa figury $G$ do figury $F$ .

Własności podobieństwa

Własność: Własności podobieństwa

Własności podobieństwa:

zachowuje stosunek odcinków,

przekształca kąt w kąt do niego przystający,

zachowuje współliniowość i uporządkowanie punktów na prostej.

O figurach, mających ten sam kształt, a różniących się co najwyżej wielkością mówimy, że są podobne.

Wprowadźmy definicję wielokątów podobnych.

Wielokąty podobne

Definicja: Wielokąty podobne

O dwóch wielokątach mówimy, że są podobne, jeśli miary ich kątów są odpowiednio równe, a długości odpowiednich boków są proporcjonalne.

R1YUQXOJCZ9OT

Na ilustracji przedstawiono dwa pięciokąty, różniące się długością boków. Długości boków mniejszego pięciokąta oznaczono a, b, c, d, e. Długości boków drugiego pięciokąta oznaczono a', b', c', d', e'. Kąty w obu pięciokątach między odpowiadającymi sobie bokami, są takie same. Zaznaczono kąt α, β, γ, ϖ, ε.

Zatem

\frac{a'}{a} = \frac{b'}{b} = \frac{c'}{c} = \frac{d'}{d} = \frac{e'}{e}

Współczynnik proporcjonalności odpowiadających sobie boków w wielokątach podobnych będziemy nazywać skalą podobieństwaskala podobieństwaskalą podobieństwa i oznaczać jako $k$ .

Załóżmy, że trójkąty $A' B' C'$ i $A B C$ z rysunków są podobne.

R1NiwyoLXXA9D

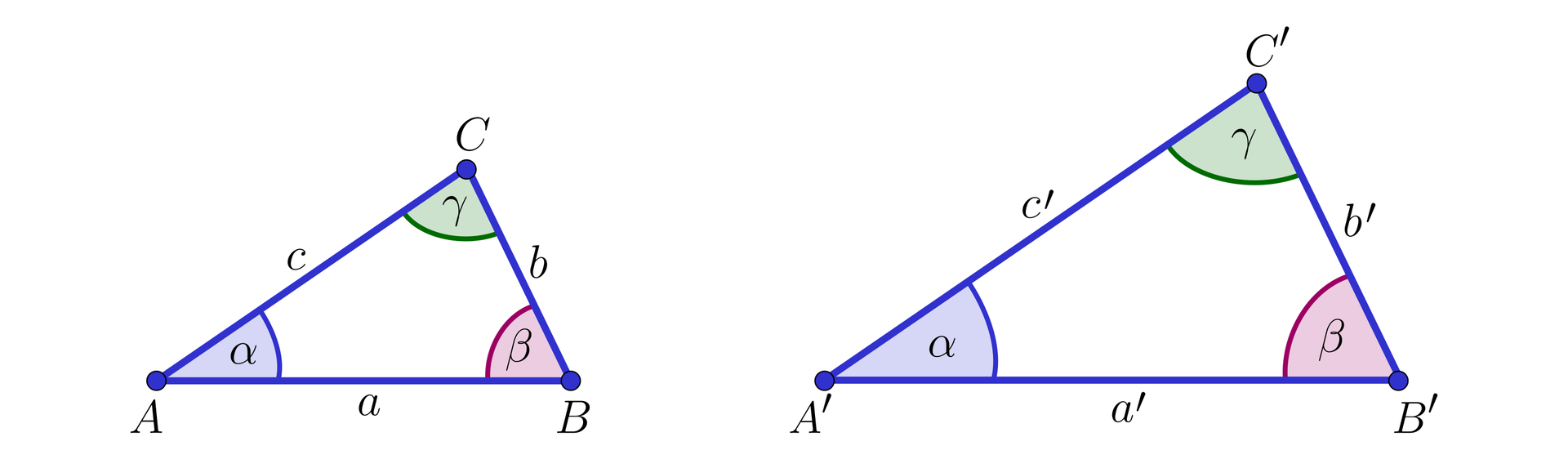
Na ilustracji przedstawiono trójkąt ABC, oraz A'B'C'. W obu trójkątach zaznaczono kąty α, β i γ. Odpowiednio przy wierzchołkach A i A' znajduje się kąt α. Przy wierzchołkach B i B' znajduje się kąt β. Przy wierzchołkach C i C' znajduje się kąt γ.

Wówczas skalę podobieństwa $k$ tych trójkątów obliczamy z zależności:

k = \frac{a'}{a} = \frac{b'}{b} = \frac{c'}{c}

o skali podobieństwa

Twierdzenie: o skali podobieństwa

Jeżeli figura o obwodzie długości $L'$ jest podobna do figury o obwodzie długości $L$ , to skalę podobieństwa tych figur obliczamy ze wzoru:

k = \frac{L'}{L}

Dowód

Załóżmy bez utraty ogólności, że trójkąt $A' B' C'$ jest podobny do trójkąta $A B C$ w skali $k$ .

R14UACUIs1Arn

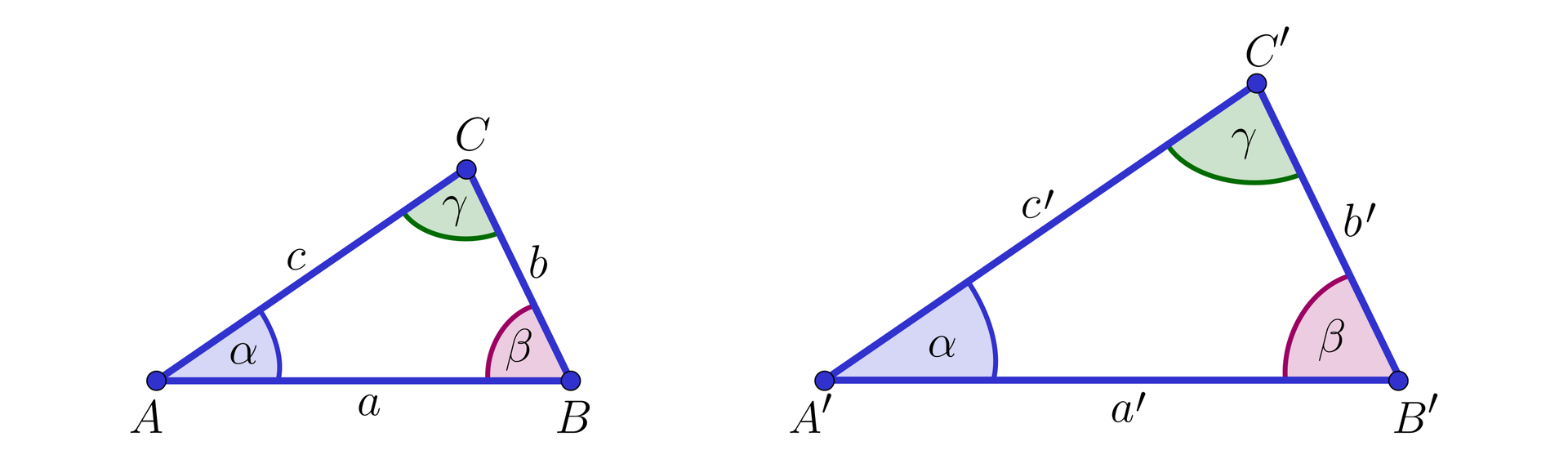
Zatem:

$k = \frac{a'}{a}$ , czyli $a' = k \cdot a$

$k = \frac{b'}{b}$ , czyli $b' = k \cdot b$

$k = \frac{c'}{c}$ , czyli $c' = k \cdot c$

Wobec tego:

$\frac{L'}{L} = \frac{a' + b' + c'}{a + b + c} = \frac{k \cdot a + k \cdot b + k \cdot c}{a + b + c} = \frac{k \cdot (a + b + c)}{a + b + c} = k$

Jeżeli skala podobieństwa $k = 1$ , to przekształcenie jest izometriąizometriaizometrią.

o skali figur podobieństwa figur podobnych

Twierdzenie: o skali figur podobieństwa figur podobnych

Jeżeli figura $F$ jest podobna do figury $G$ w skali $k$ , to figura $G$ jest podobna do figury $F$ w skali $\frac{1}{k}$ .

Ważne!

Każde dwa wielokąty foremne, mające tę samą liczbę boków są podobne.

Każde dwa odcinki są podobne.

Każde dwa koła są podobne.

Przykład 1

Sprawdzimy, czy równoległoboki przedstawione na poniższych rysunkach są podobne.

RA4xrb3LBSYmx

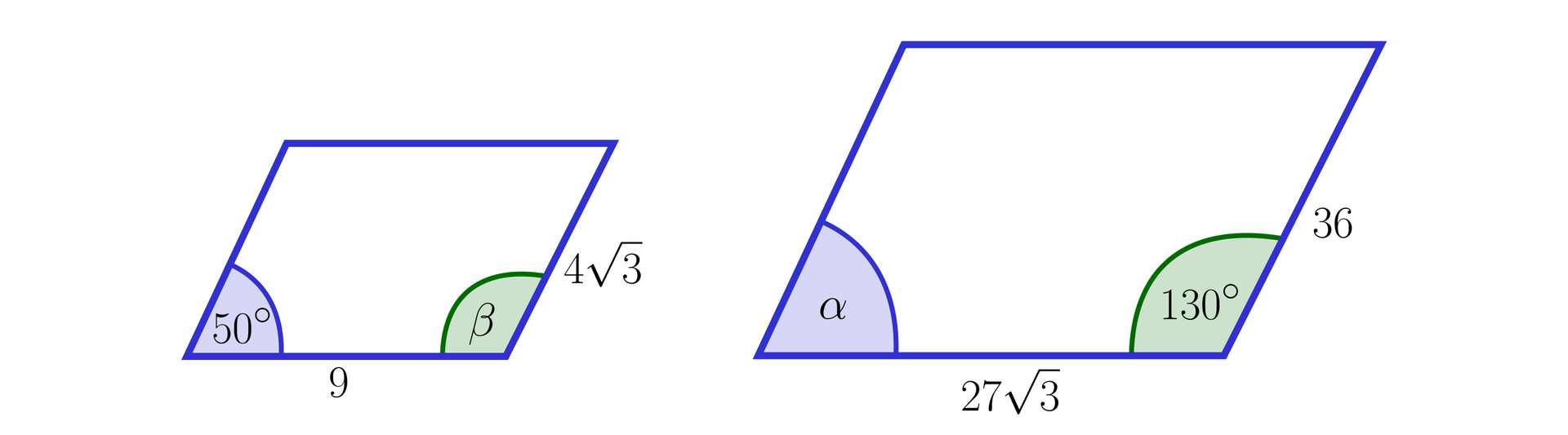
Na ilustracji przedstawiono dwa równoległoboki różniące się długością boków. Zaznaczono ich kąty wewnętrzne. W równoległoboku pierwszym, długość dłuższego boku jest równa 9, natomiast długość krótszego boku wynosi 43. Kąt ostry między bokami wynosi 50°, natomiast kąt rozwarty jest równy β. W drugim równoległoboku, długość krótszego boku wynosi 273, natomiast długość dłuższego boku wynosi trzydzieści sześć. Kąt ostry między bokami wynosi α, natomiast kąt rozwarty między bokami wynosi 130°.

Rozwiązanie:

Ponieważ figury przedstawione na rysunkach są równoległobokami, zatem $α = 50 °$ oraz $β = 130 °$ .

Jeżeli figury mają te same kąty, to wystarczy sprawdzić, czy odpowiednie boki są proporcjonalne.

Wobec tego:

$\frac{36}{4 \sqrt{3}} = \frac{27 \sqrt{3}}{9}$

Ponieważ równość jest prawdziwa, zatem równoległoboki z rysunku są podobne.

Przykład 2

Trójkąt prostokątny $T_{1}$ o przyprostokątnych długości $12$ i $16$ jest podobny do trójkąta prostokątnego $T_{2}$ o przeciwprostokątnej długości $40 \sqrt{2}$ . Obliczymy obwód trójkąta $T_{2}$ .

Rozwiązanie:

Narysujmy rysunki pomocnicze trójkątów $T_{1}$ i $T_{2}$ i wprowadźmy odpowiednie oznaczenia:

RU3u65mRyKZx5

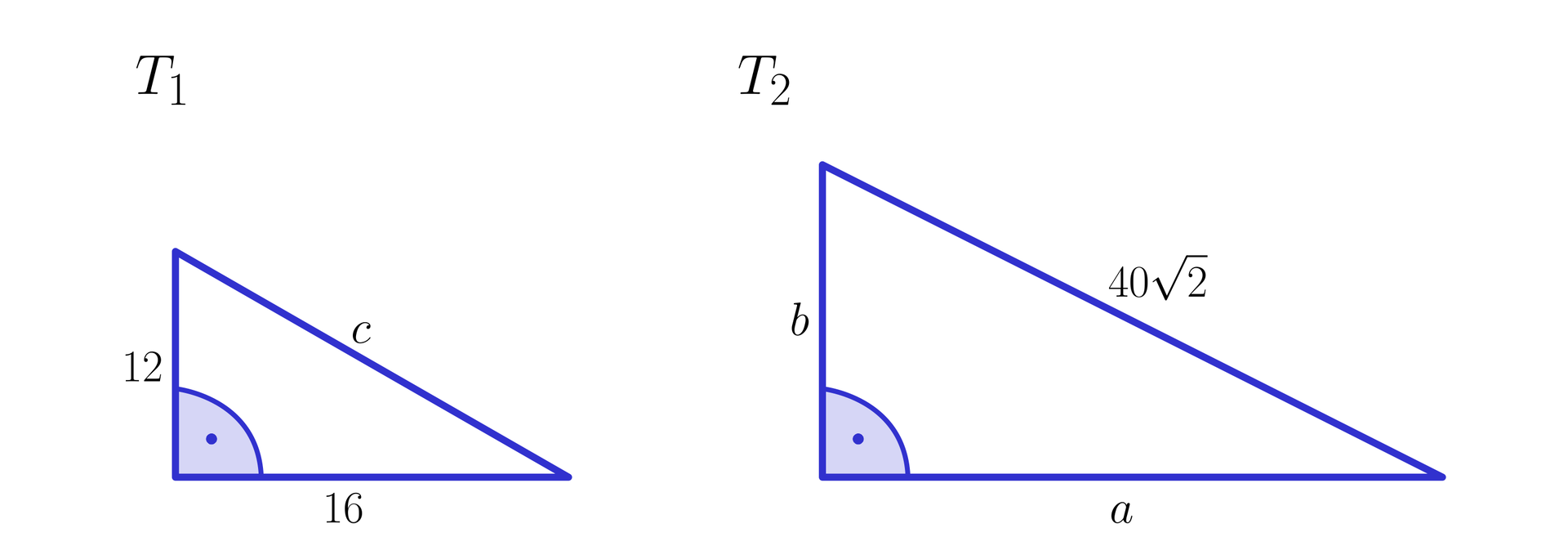
Na ilustracji przedstawiono dwa trójkąty prostokątne, które są względem siebie podobne. Mniejszy trójkąt T1, oraz większy T2. W trójkącie T1, przyprostokątne są długości 12 i 16, natomiast przeciwprostokątną oznaczono małą literą c. W trójkącie T2a, przyprostokątne oznaczono a i b, natomiast długość przeciwprostokątnej jest równa 402.

Korzystając z twierdzenia Pitagorasa, obliczamy długość przeciwprostokątnej $c$ trójkąta $T_{1}$ .

Zatem

$12^{2} + 16^{2} = c^{2}$

$c^{2} = 400$

$c = 20$

Obliczamy skalę podobieństwa $k$ trójkąta $T_{2}$ do trójkąta $T_{1}$ .

Wobec tego:

$k = \frac{40 \sqrt{2}}{20} = 2 \sqrt{2}$

$2 \sqrt{2} = \frac{a}{16}$

$a = 32 \sqrt{2}$

$2 \sqrt{2} = \frac{b}{12}$

$b = 24 \sqrt{2}$

Zatem obwód trójkąta $T_{2}$ jest równy:

$L = 24 \sqrt{2} + 32 \sqrt{2} + 40 \sqrt{2} = 96 \sqrt{2}$

Ważne!

Jeżeli dwie figury są podobne, to każde odpowiadające sobie odcinki w obu figurach są do siebie proporcjonalne. Tymi odcinkami są (o ile istnieją) wysokości, przekątne, środkowe itp.

Przykład 3

Dwa romby są podobne w skali $\frac{5}{3}$ . Obliczymy obwód każdego z nich, jeżeli długości przekątnych mniejszego rombu są równe $4 \sqrt{3}$ i $4$ .

Rozwiązanie:

Narysujmy dwa romby $R_{1}$ i $R_{2}$ , które są podobne i wprowadźmy oznaczenia, jak na poniższych rysunkach.

RzZ7AmHKF8iY9

Na ilustracji przedstawiono dwa romby które są względem siebie podobne. Mniejszy romb R1 i większy romb R2. W rombie R1 długość boku oznaczono małą literą a. Długość dłuższej przekątnej wynosi 43, natomiast długość krótszej przekątnej jest równa cztery. W rombie R2 oznaczono jedynie bok a'.

Korzystając z twierdzenia Pitagorasa, obliczamy długość boku mniejszego rombu.

Zatem:

$a^{2} = {(2 \sqrt{3})}^{2} + 2^{2}$

$a^{2} = 16$

$a = 4$

Ponieważ skala $k = \frac{5}{3}$ , zatem:

$k = \frac{a'}{a}$

$\frac{5}{3} = \frac{a'}{4}$

$a' = \frac{20}{3}$

Wobec tego obwody rombów $R_{1}$ i $R_{2}$ wynoszą odpowiednio:

$L = 4 \cdot 4 = 16$

$L' = 4 \cdot \frac{20}{3} = \frac{80}{3}$

Przykład 4

Dane są równoległoboki $A B C D$ oraz $A' B' C' D'$ , które są podobne. Krótsza przekątna równoległoboku $A B C D$ tworzy z jego krótszym bokiem kąt prosty. Obliczymy obwody obu równoległoboków, jeżeli boki równoległoboku $A B C D$ wynoszą $6$ i $12$ , a krótsza przekątna równoległoboku $A' B' C' D'$ ma długość $8 \sqrt{3}$ .

Rozwiązanie:

Narysujmy równoległoboki $A B C D$ oraz $A' B' C' D'$ , które są podobne oraz wprowadźmy oznaczenia, jak na rysunkach.

R1KdOoyVg6A4G

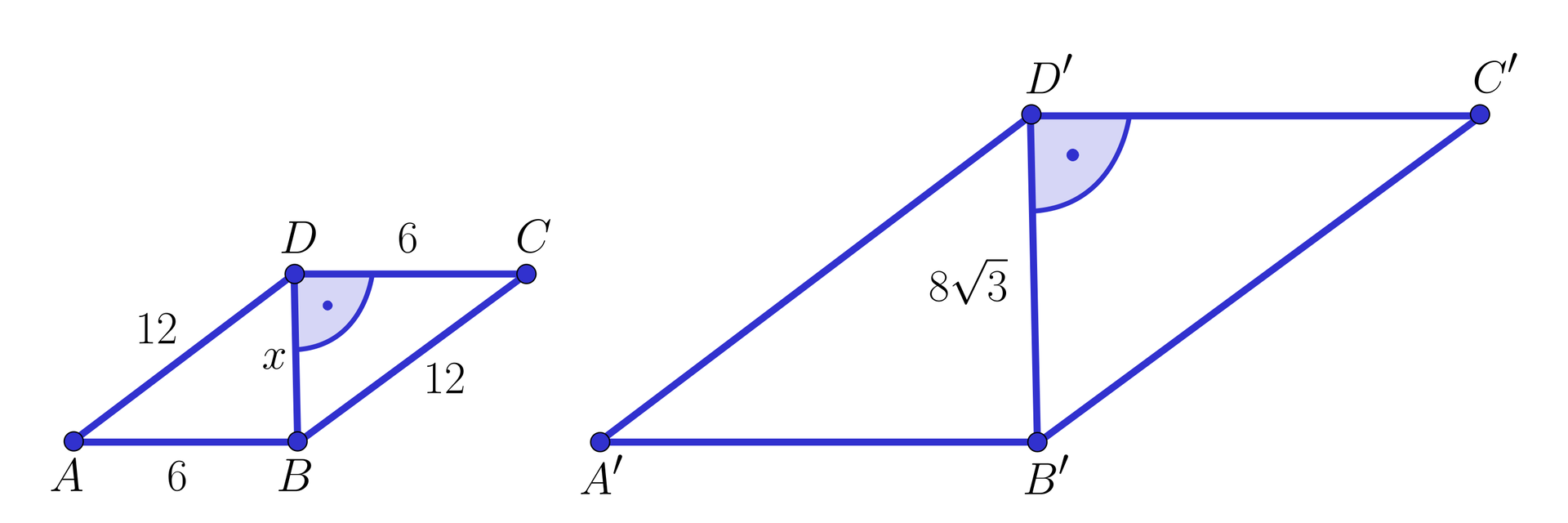
Na ilustracji przedstawiono mniejszy równoległobok ABCD, oraz większy A'B'C'D'. Równoległoboki są względem siebie podobne. W równoległoboku ABCD, długość krótszego boku wynosi 6, natomiast długość dłuższego boku jest równa dwanaście. Wewnątrz tego równoległoboku zaznaczono przekątną x. W równoległoboku A'B'C'D' zaznaczono przekątną wewnątrz figury, jest równa 83.

Korzystając z twierdzenia Pitagorasa obliczamy długość przekątnej $x$ w równoległoboku $A B C D$ .

Zatem

$x^{2} + 6^{2} = 12^{2}$

$x^{2} + 36 = 144$

$x^{2} = 108$

$x = 6 \sqrt{3}$ .

Niech $k$ będzie skalą podobieństwa równoległoboku $A' B' C' D'$ do równoległoboku $A B C D$ .

Wtedy $k = \frac{8 \sqrt{3}}{6 \sqrt{3}} = \frac{4}{3}$ .

Obwód $L$ równoległoboku $A B C D$ wynosi:

$L = 2 \cdot 6 + 2 \cdot 12 = 12 + 24 = 36$ .

Niech $L'$ będzie obwodem równoległoboku $A' B' C' D'$ .

Jeżeli skala podobieństwa $A' B' C' D'$ do równoległoboku $A B C D$ wynosi $\frac{4}{3}$ , to:

$\frac{4}{3} = \frac{L'}{36}$ .

Wobec tego $L' = 48$ .

Zatem obwody omawianych równoległoboków wynoszą odpowiednio $36$ i $48$ .

Przykład 5

Wiadomo, że suma obwodów dwóch figur podobnych wynosi $224$ . Wyznaczymy obwody tych figur, jeżeli wiadomo, że ich skala podobieństwa wynosi $\frac{2}{5}$ .

Rozwiązanie:

Niech $L_{1}$ i $L_{2}$ będą obwodami dwóch figur podobnych.

Do wyznaczenia wartości $L_{1}$ i $L_{2}$ rozwiązujemy układ równań:

$\{\begin{cases} L_{1} + L_{2} = 224 \\ \frac{L_{1}}{L_{2}} = \frac{2}{5} \end{cases}$

Układ równań przekształcamy do postaci:

$\{\begin{cases} L_{1} + L_{2} = 224 \\ L_{1} = \frac{2}{5} \cdot L_{2} \end{cases}$

Wobec tego:

$\frac{2}{5} L_{2} + L_{2} = 224$

$\frac{7}{5} L_{2} = 224$

$L_{2} = 224 \cdot \frac{5}{7} = 160$

Zatem:

$L_{1} = 224 - 160 = 64$

Zatem obwody tych figur wynoszą odpowiednio $64$ i $160$ .

Słownik

podobieństwo

przekształcenie geometryczne, które zachowuje stosunek odległości punktów płaszczyzny

przystawanie

identyczność kształtu i wielkości figur

cechy podobieństwa trójkątów

warunki konieczne i wystarczające, aby dwa trójkąty były podobne

izometria

przekształcenie geometryczne, przy którym odległość punktów nie ulega zmianie, np. przesunięcie równoległe, obrót, symetria względem prostej, punktu lub płaszczyzny

skala podobieństwa

liczba dodatnia, wyrażająca stosunek odpowiadających sobie odcinków w figurach podobnych

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik