Przeczytaj

Najpierw dowiesz się, czym jest kąt nachylenia prostejkąt nachylenia prostejkąt nachylenia prostej do osi $X$ .

Naszkicujmy prostą o równaniu $y = a x + b$ w prostokątnym układzie współrzędnych. Kątem nachylenia prostej do osi $X$ nazwiemy kąt o wierzchołku w punkcie przecięcia tej prostej z osią $X$ . Jedno z ramion zawiera się w osi $X$ i jest zwrócone w tę stronę, w którą odcięte rosną, zaś drugie ramię zawiera się w tej części prostej, która leży nad osią $X$ .

Dodajmy, że na rysunkach poniżej widzimy tzw. kąty skierowane, których pewna właściwość jest dla nas istotna. Otóż kątem skierowanym nazwiemy kąt wykreślony przez dwie uporządkowane półproste, z których jedna (tu część osi $X$ ) jest ramieniem początkowym, a druga ramieniem końcowym (część prostej). Wierzchołkiem tego kąta jest punkt wspólny półprostych, które go tworzą. Kąt taki jest dodatni, jeśli ramię końcowe „przesuwa się” przeciwnie do ruchu wskazówek zegara (jak na rysunku). Kąt skierowany ujemny natomiast jest zakreślony w przeciwną stronę (zgodnie z ruchem wskazówek zegara). Aby określić kąt nachylenia prostej do osi $X$ , będziemy rozpatrywać jedynie kąty skierowane dodatnie.

RC3lhlvJXLXBk

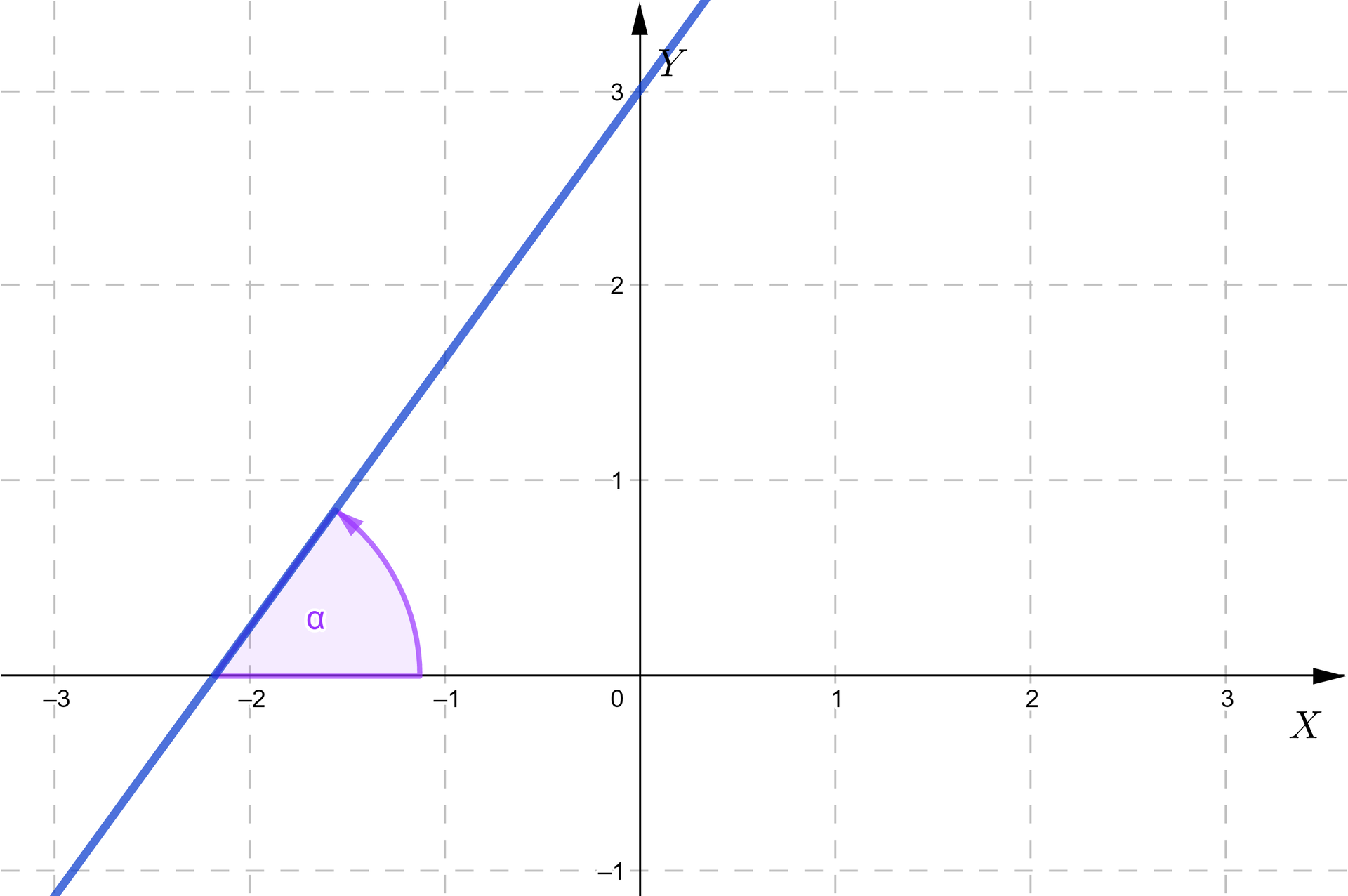
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus trzech do trzech oraz z pionową osią Y od minus jeden do trzech. Na płaszczyźnie narysowana jest ukośna prosta, która przecina oś X w punkcie minus 2 i dwie dziesiąte zero i oś Y w punkcie 0 3. Prosta tworzy z osią X kąt ostry alfa.

RobCxPrHR3uDN

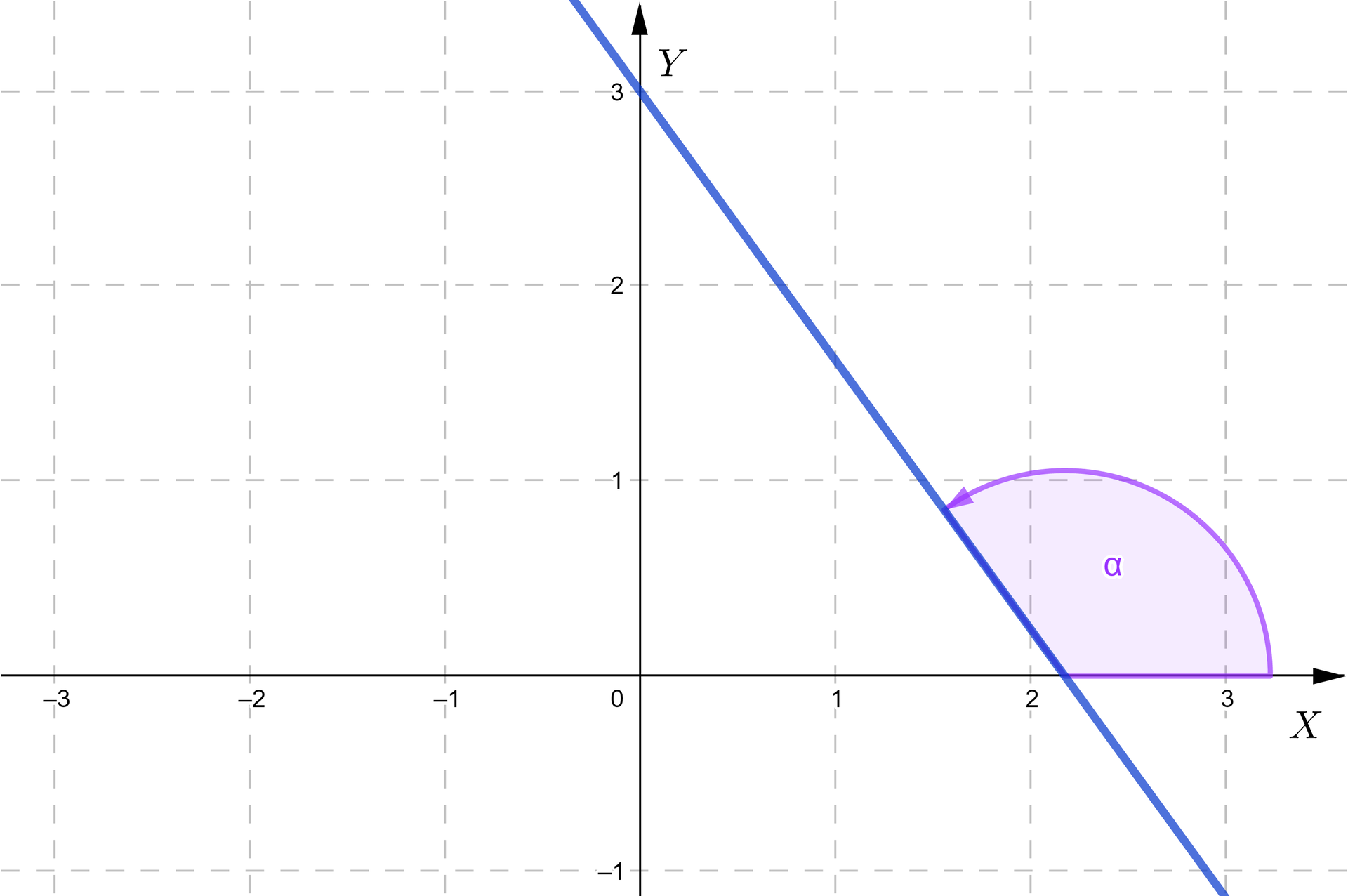
Jak można zauważyć z powyższych rysunków, kąt ten ma miarę z przedziału od $0^{\circ}$ do $180^{\circ}$ .

R91DNHgMx3SOx

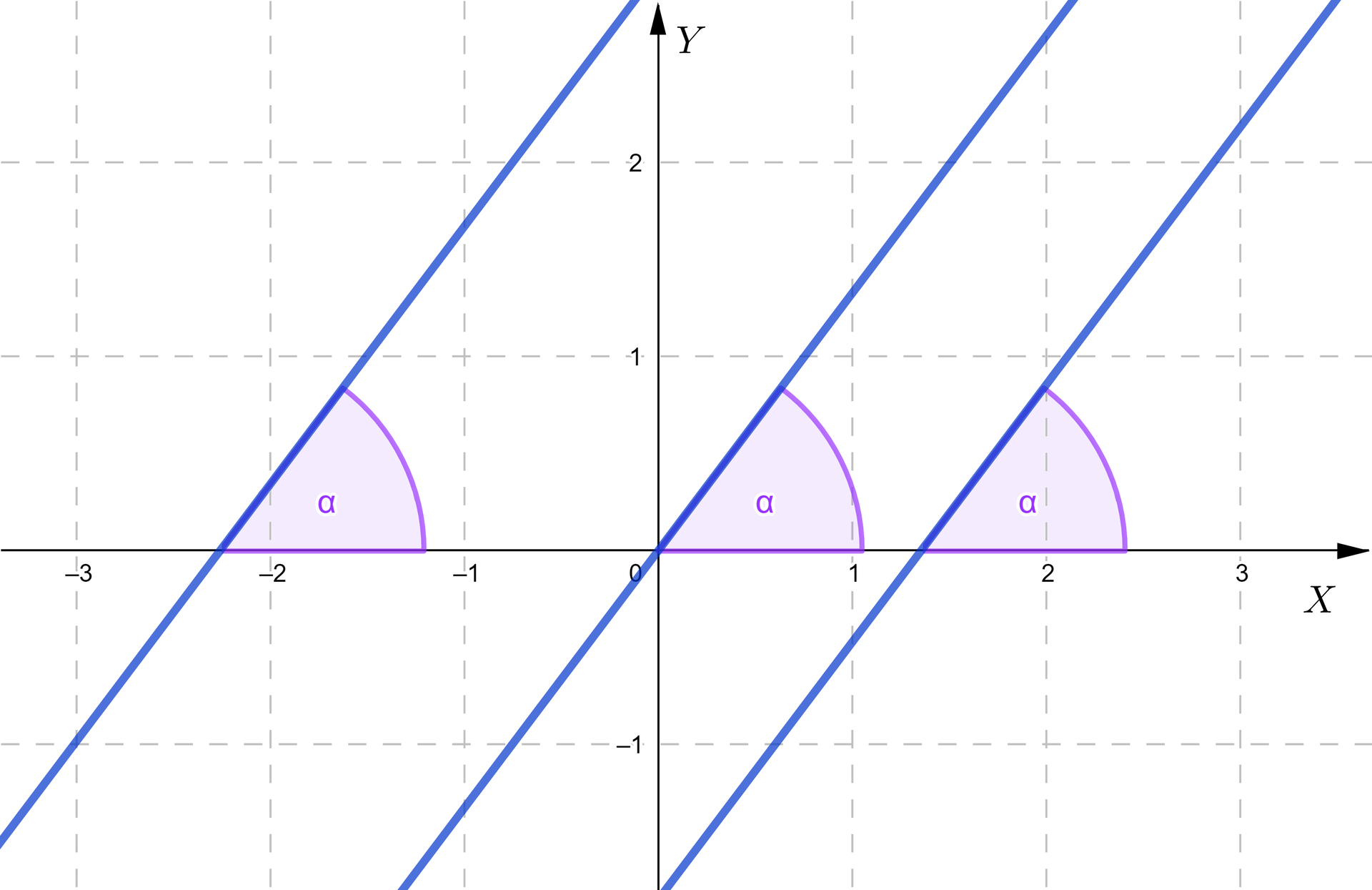
Wszystkie proste nachylone do osi $X$ pod tym samym kątem są równoległe, co możemy zauważyć na powyższym rysunku. Dlatego też w dalszej części rozważymy proste nierównoległe, przechodzące przez początek układu współrzędnych, których wyraz wolny $b$ jest równy zero. To pozwoli nam zauważyć zależność między współczynnikiem kierunkowym prostej a jej nachyleniem do osi $X$ .

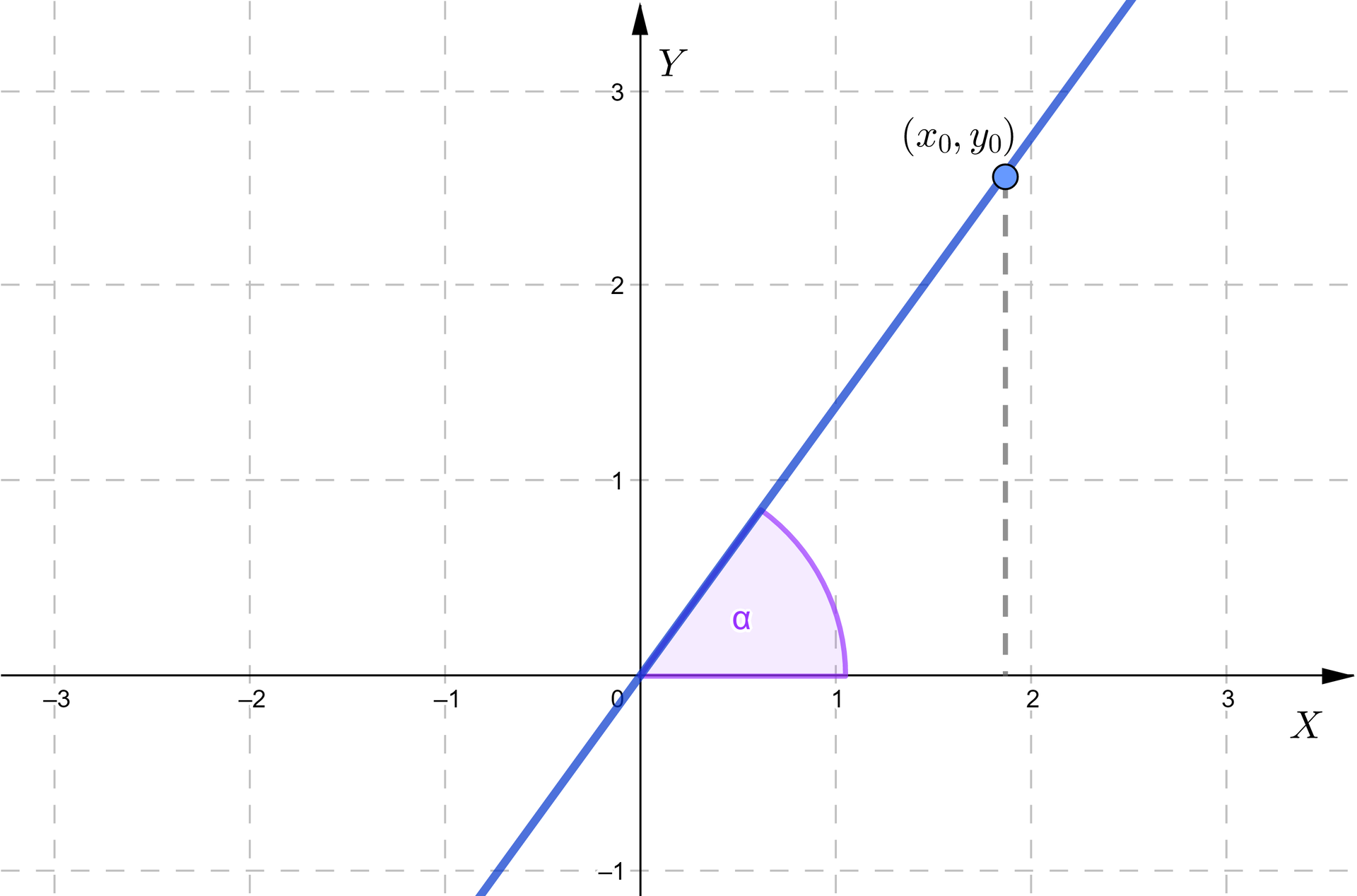
Rozważmy prostą o równaniu $y = a x$ i wybierzmy w niej jeden punkt o współrzędnych $(x_{0}, y_{0})$ leżący na tej części prostej, która znajduje się ponad osią $X$ . Wówczas punkt ten spełnia równanie prostej, zatem otrzymujemy równość $y_{0} = a x_{0}$ , która jest równoważna równości $a = \frac{y_{0}}{x_{0}}$ . Z lekcji o funkcjach trygonometrycznych kąta dowolnego wiemy, że $\frac{y_{0}}{x_{0}}$ to tangens kąta. Stąd możemy wyciągnąć wniosek, że o ile kąt nachylenia prostejkąt nachylenia prostejkąt nachylenia prostej do osi $X$ nie jest prosty, to jego tangens jest równy współczynnikowi kierunkowemu tej prostej.

Ważne!

Dla prostej o równaniu $y = a x + b$ i kącie $α$ nachylenia do osi $X$ zachodzi związek: $a = tg α$ , gdzie $α \in (0 °, 90 °) \cup (90 °, 180 °)$ .

RqPdbT6qL8b9I

Przykład 1

Wyznaczymy równanie prostej przechodzącej przez początek układu współrzędnych nachylonej do osi $X$ pod kątem:

a) $α = 60 °$

RS5rJSZSr7Rww

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus trzech do trzech oraz z pionową osią Y od minus dwóch do dwóch. Na płaszczyźnie narysowana jest ukośna prosta, która przechodzi przez punkt 0 0 i tworzy z osią X kąt alfa równy 60 stopni.

Ponieważ prosta przechodzi przez początek układu współrzędnych, to ma równanie kierunkowe postaci $y = a x$ . Kąt nachylenia tej prostej to $60 °$ , zatem $a = tg 60^{\circ} = \sqrt{3}$ , czyli prosta ma równanie $y = \sqrt{3} x$ .

b) $β = 150 °$

R170vFWOEscLm

Ponieważ prosta przechodzi przez początek układu współrzędnych, to ma równanie kierunkowe postaci $y = a x$ . Kąt nachylenia tej prostej to $150 °$ , zatem $a = tg 150 ° = - \frac{\sqrt{3}}{3}$ , czyli prosta ma równanie $y = - \frac{\sqrt{3}}{3} x$ .

Przykład 2

Wyznaczymy kąty nachylenia do osi $X$ prostych o podanych równaniach.

a) $y = \frac{\sqrt{3}}{3} x + 2$

Ponieważ współczynnik kierunkowy prostej jest dodatni i równy $\frac{\sqrt{3}}{3}$ oraz jej kąt nachylenia do osi $X$ jest między $0 °$ a $180 °$ , więc szukany kąt jest ostry. Kąt ostry, którego tangens jest równy $\frac{\sqrt{3}}{3}$ , ma miarę $30 °$ .

b) $y = - \sqrt{3} x - 3$

Ponieważ współczynnik kierunkowy prostej jest ujemny i równy $- \sqrt{3}$ oraz jej kąt nachylenia do osi $X$ jest między <math”> a $180 °$ , więc szukany kąt jest rozwarty. Kąt rozwarty, którego tangens jest równy $- \sqrt{3}$ , ma miarę $120 °$ .

Rzeczywiście $tg 120 ° = tg (90 ° + 30 °) = - ctg 30 ° = - \sqrt{3}$ .

Przykład 3

Wyznaczymy równanie prostej nachylonej do osi $X$ pod kątem $135 °$ , która przecina oś $Y$ w punkcie o rzędnej $- 3$ .

RDwWyHUT4reJc

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do dwóch oraz z pionową osią Y od minus trzech do jeden. Na płaszczyźnie narysowana jest ukośna prosta, która przechodzi przez punkt minus 3 0 i tworzy z osią X kąt równy 135 stopni.

Ponieważ prosta nie jest równoległa do osi $Y$ , wystarczy rozważyć równanie kierunkowe $y = a x + b$ tej prostej. Skorzystamy z interpretacji współczynnika kierunkowego jako tangensa kąta nachylenia. Wynika z niej, że: $a = tg 135 ° = tg (90 ° + 45 °) = - ctg 45 ° = - 1$ . Zatem prosta ma równanie postaci $y = - x + b$ . Wyraz wolny $b$ możemy wyznaczyć, korzystając z faktu, że prosta przecina oś $Y$ w punkcie o współrzędnych $(0, - 3)$ . Z interpretacji graficznej współczynnika $b$ możemy wywnioskować, że $b = - 3$ . Zatem szukane równanie prostej to $y = - x - 3$ .

Przykład 4

Wyznaczymy równanie prostej nachylonej do osi $X$ pod kątem $150 °$ , która przechodzi przez punkt o współrzędnych $(3, 1)$ .

RVFCVHO30Lm5h

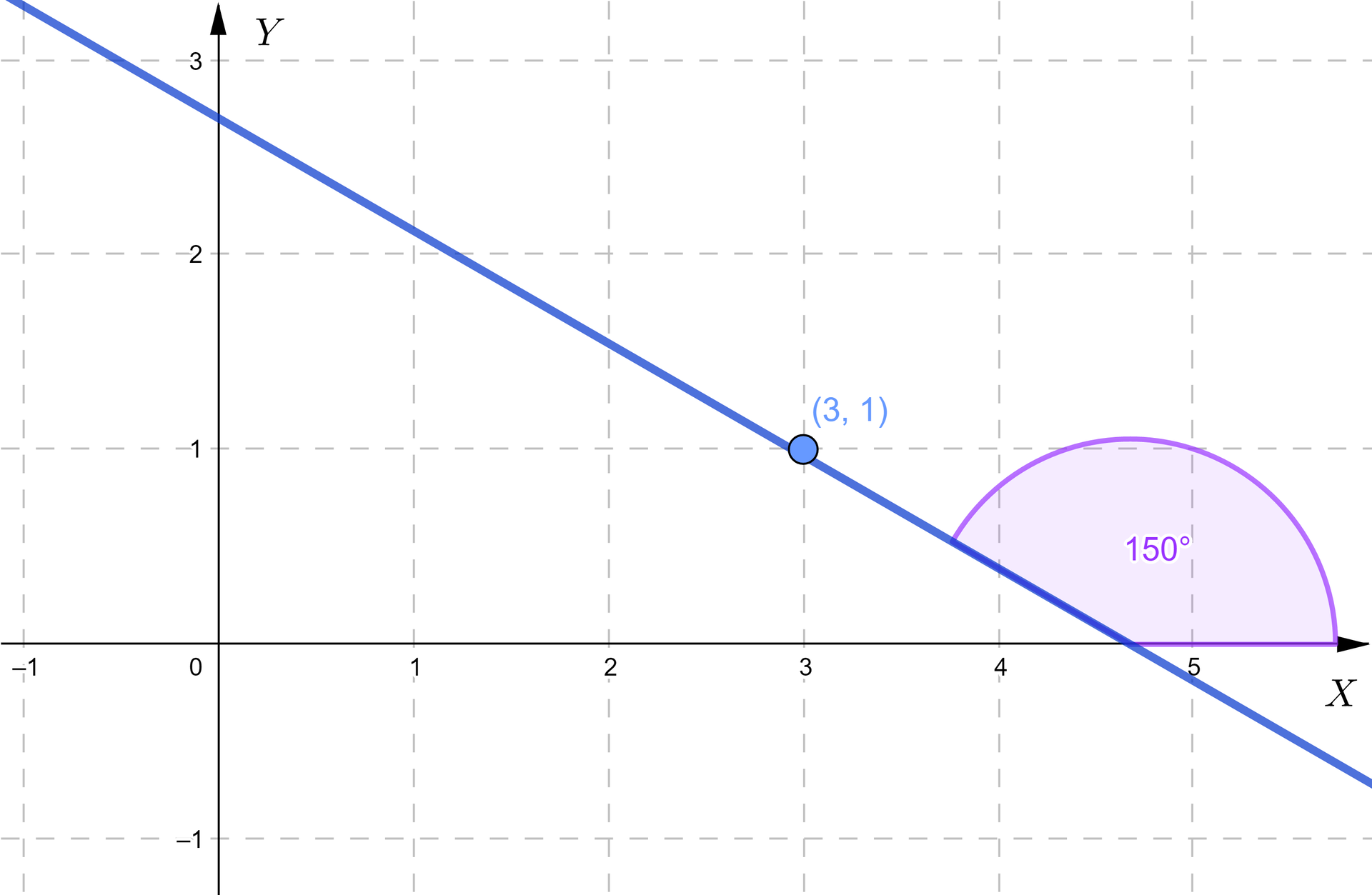
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do pięciu oraz z pionową osią Y od minus jeden do trzech. Na płaszczyźnie narysowana jest ukośna prosta, która przechodzi przez punkt cztery i siedem dziesiątych 0 i tworzy z osią X kąt równy 150 stopni. Na prostej zaznaczony jest punkt o współrzędnych 3 1.

Ponieważ prosta nie jest pionowa, wystarczy rozważyć równanie kierunkowe $y = a x + b$ tej prostej. Skorzystamy z interpretacji współczynnika kierunkowego jako tangensa kąta nachylenia.

Wynika z niego, że: $a = tg 150 ° = tg (90 ° + 60 °) = - ctg 60 ° = - \frac{\sqrt{3}}{3}$ .

Zatem prosta ma równanie postaci $y = - \frac{\sqrt{3}}{3} x + b$ . Wyraz wolny $b$ możemy wyznaczyć, korzystając z faktu, że prosta przechodzi przez punkt o współrzędnych $(3, 1)$ . Możemy do równania $y = - \frac{\sqrt{3}}{3} x + b$ podstawić $x = 3$ oraz $y = 1$ :

$1 = - \frac{\sqrt{3}}{3} \cdot 3 + b$

$1 = - \sqrt{3} + b$

$\sqrt{3} + 1 = b$ .

Zatem szukane równanie prostej to $y = - \frac{\sqrt{3}}{3} x + \sqrt{3} + 1$ .

Zastosujemy teraz interpretację współczynnika kierunkowego prostej do rozwiązania problemu z geometrii analitycznej.

Przykład 5

Wierzchołki $A$ i $B$ trójkąta równoramiennego $A B C$ znajdują się na paraboli o równaniu $y = \frac{1}{4} {(x - 4)}^{2}$ oraz na prostej równoległej do osi $X$ . Punkt $C$ jest jednocześnie wierzchołkiem paraboli. Wyznacz współrzędne punktów $A$ , $B$ , $C$ jeśli wiadomo, że kąt rozwarty tego trójkąta ma miarę $120 °$ .

R10MtuTElGANx

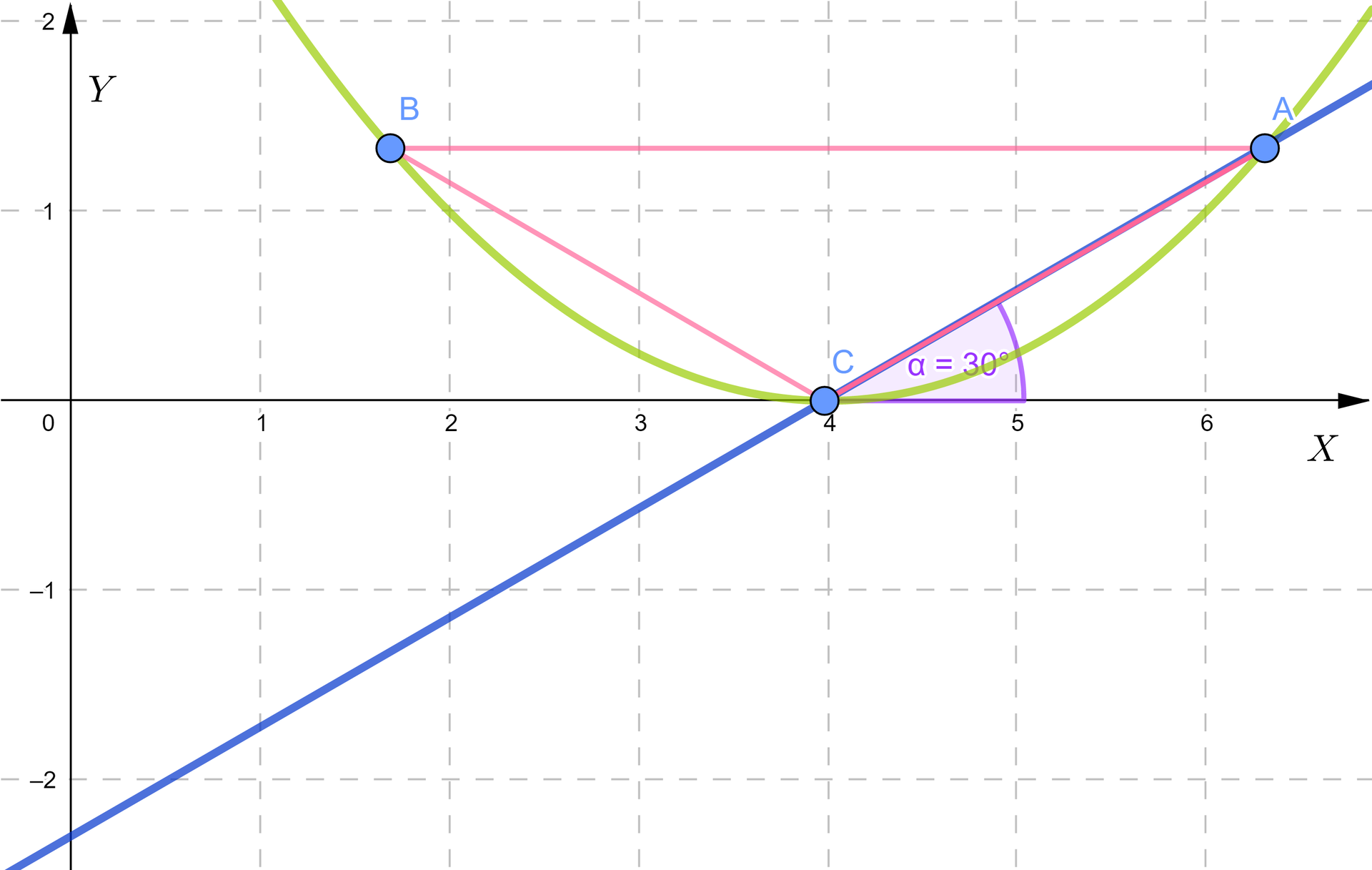
Ilustracja przedstawia układ współrzędnych z poziomą osią X od zera do sześciu oraz z pionową osią Y od minus dwóch do dwóch. Na płaszczyźnie narysowana jest ukośna prosta, która przechodzi przez punkty 0 minus dwa i trzy dziesiąte oraz cztery zero. Prosta tworzy z osią X kąt alfa równy 30 stopni. Na płaszczyźnie narysowana jest także parabola o ramionach skierowanych do góry i wierzchołku w punkcie C o współrzędnych 4 0. Na prostej zaznaczone są dwa punkty przecięcia z parabolą: punkt C oraz punkt A na prawym ramieniu paraboli. Na lewym ramieniu paraboli zaznaczony jest również punkt B, który jest symetryczny do punktu A względem pionowej prostej przechodzącej przez wierzchołek paraboli o równaniu X równa się 4. Punkty A, B i C są połączone odcinkami tworzącymi trójkąt równoramienny CAB.

Po pierwsze obliczymy współrzędne punktów szczególnych paraboli: punktów jej przecięcia z osią $X$ oraz wierzchołka:

Z podanego równania możemy odczytać, że jedynym punktem wspólnym paraboli z osią $X$ jest punkt o współrzędnych $(4, 0)$ . Są to jednocześnie współrzędne wierzchołka paraboli oraz punktu $C$ , który jest wierzchołkiem kąta o mierze $120 °$ .

Po drugie wyznaczymy równanie prostej $A C$ :

Zauważmy, że prosta $A C$ jest nachylona do osi $X$ pod kątem $30 °$ , zatem jej współczynnik kierunkowy jest równy $a = tg 30 ° = \frac{\sqrt{3}}{3}$ . Zatem równanie prostej ma postać $y = \frac{\sqrt{3}}{3} x + b$ .
Wyraz wolny $b$ prostej $A C$ możemy wyznaczyć podstawiając do równania $y = \frac{\sqrt{3}}{3} x + b$ współrzędne punktu $C = (4, 0)$ : $0 = \frac{\sqrt{3}}{3} \cdot 4 + b$ wtedy i tylko wtedy, gdy $b = - \frac{4 \sqrt{3}}{3}$ . Równanie prostej $A C$ to $y = \frac{\sqrt{3}}{3} x - \frac{4 \sqrt{3}}{3}$ .

Po trzecie wyznaczymy współrzędne punktu $A$ :

Ponieważ punkt $A$ leży i na prostej $A C$ , i na paraboli, więc jego współrzędne możemy wyznaczyć, rozwiązując układ równań $\{\begin{cases} y = \frac{\sqrt{3}}{3} x - \frac{4 \sqrt{3}}{3} \\ y = \frac{1}{4} {(x - 4)}^{2} \end{cases}$ .
Z układu równań wynika równanie: $\frac{1}{4} {(x - 4)}^{2} = \frac{\sqrt{3}}{3} x - \frac{4 \sqrt{3}}{3}$ , które jest równoważne z równaniem: $3 x^{2} + (- 24 - 4 \sqrt{3}) x + 48 + 16 \sqrt{3} = 0$ .
Obliczymy pierwiastki tego równania: $∆ = {(- 24 - 4 \sqrt{3})}^{2} - 4 \cdot 3 \cdot (48 + 16 \sqrt{3}) = 48 = {(4 \sqrt{3})}^{2}$ . Pierwiastkami powyższego równania kwadratowego są liczby $x_{1} = \frac{(24 + 4 \sqrt{3} - 4 \sqrt{3})}{6} = 4$ i $x_{2} = \frac{(24 + 4 \sqrt{3} + 4 \sqrt{3})}{6} = 4 + \frac{4 \sqrt{3}}{3}$ .
Drugą współrzędną punktu $A$ obliczymy podstawiając $x = 4 + \frac{4 \sqrt{3}}{3}$ do równania paraboli: $y = \frac{1}{4} {(4 + \frac{4 \sqrt{3}}{3} - 4)}^{2} = \frac{4}{3}$ .
Zatem współrzędne punktów przecięcia prostej $A C$ i paraboli to $C = (4, 0)$ i $A = (4 + \frac{4 \sqrt{3}}{3}, \frac{4}{3})$ .
Ponieważ punkty $A$ i $B$ są położone symetrycznie względem prostej o równaniu $x = 4$ , więc punkt $B$ ma współrzędne $(4 - \frac{4 \sqrt{3}}{3}, \frac{4}{3})$ .

Słownik

kąt nachylenia prostej

kąt jaki tworzy prosta z dodatnią półosią $X$ .

Wprowadzenie

Aplet

Słownik