Przeczytaj

Często chcemy obliczyć długość jakiegoś odcinka w trójkącie. Jednym z takich odcinków jest środkowa trójkąta.

Przeanalizujmy sposób postępowania w rozwiązaniu tego zagadnienia.

Przykład 1

Wyprowadzimy wzór na długość środkowej $A D$ trójkąta $A B C$ o bokach długości $a = |B C|$ , $b = |A C|$ , $c = |A B|$ .

Rozwiązanie

$I$ sposób:
Przyjmijmy standardowe oznaczenia trójkąta oraz oznaczmy długość środkowej $A D$ symbolem $m_{a}$ , jak na rysunku.
R10FBvwUPPPLZ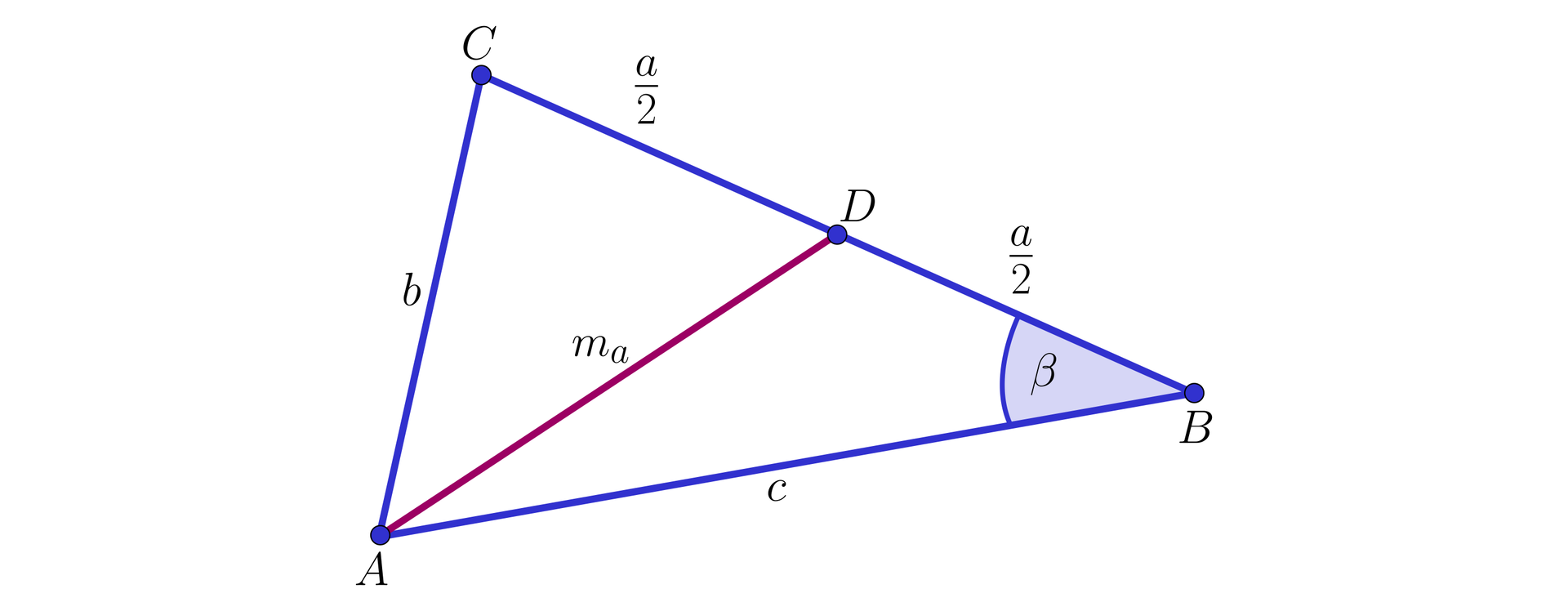
Z twierdzenia cosinusów zastosowanego dla kąta $β$ w trójkątach $A B C$ i $A B D$ otrzymujemy
$b^{2} = a^{2} + c^{2} - 2 a c \cos β$ oraz $m_{a}^{2} = {(\frac{1}{2} a)}^{2} + c^{2} - 2 \cdot \frac{1}{2} a c \cos β$ .
Ponieważ długości boków trójkąta $A B C$ mamy dane, więc otrzymany układ równań zawiera dwie niewiadome, $m_{a}$ i $\cos β$ . Wystarczy więc z jednego z tych równań wyznaczyć niewiadomą $\cos β$ i podstawić otrzymaną wielkość do drugiego równania. Otrzymamy wtedy równanie z niewiadomą $m_{a}$ .
W naszym przypadku: $\cos β = \frac{a^{2} + c^{2} - b^{2}}{2 a c}$ , więc stąd i z drugiego równania otrzymujemy
$m_{a}^{2} = {(\frac{1}{2} a)}^{2} + c^{2} - \frac{a^{2} + c^{2} - b^{2}}{2} = \frac{1}{4} a^{2} + c^{2} - \frac{1}{2} a^{2} - \frac{1}{2} c^{2} + \frac{1}{2} b^{2} =$
$= \frac{1}{2} b^{2} + \frac{1}{2} c^{2} - \frac{1}{4} a^{2} = \frac{1}{4} (2 b^{2} + 2 c^{2} - a^{2})$ ,
skąd $m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}$ .
W ten sposób wyprowadziliśmy wzór na długość środkowej trójkątawzór na długość środkowej trójkąta.

$II$ sposób:
Przyjmijmy standardowe oznaczenia trójkąta, jak na rysunku.
RmO1z7q6heAuu
Podobnie, jak w I sposobie dwukrotnie wykorzystamy twierdzenie cosinusów, ale tym razem zastosujemy je w trójkątach $A B D$ i $A C D$ dla kątów $φ$ i $180 ° - φ$ . Otrzymujmy wtedy
$c^{2} = {(\frac{1}{2} a)}^{2} + m_{a}^{2} - 2 \cdot \frac{1}{2} a \cdot m_{a} \cos φ$ oraz $b^{2} = {(\frac{1}{2} a)}^{2} + m_{a}^{2} - 2 \cdot \frac{1}{2} a \cdot m_{a} \cos (180 ° - φ)$ .
Ponieważ $\cos (180 ° - φ) = - \cos φ$ , więc otrzymane równości możemy zapisać w postaci
$c^{2} = \frac{1}{4} a^{2} + m_{a}^{2} - a m_{a} \cos φ$ oraz $b^{2} = \frac{1}{4} a^{2} + m_{a}^{2} + a m_{a} \cos φ$ .
W ten sposób otrzymaliśmy, tak jak to było w I sposobie rozwiązania, układ dwóch równań z niewiadomymi $m_{a}$ i $\cos φ$ . Dodając te równania stronami, otrzymujemy $b^{2} + c^{2} = \frac{2}{4} a^{2} + 2 m_{a}^{2}$ . Stąd $m_{a}^{2} = \frac{1}{2} b^{2} + \frac{1}{2} c^{2} - \frac{1}{4} a^{2} = \frac{1}{4} (2 b^{2} + 2 c^{2} - a^{2})$ , więc $m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}$ .

Przykład 2

Wyprowadzimy wzór na długość dwusiecznejwzór na długość dwusiecznej $A D$ trójkąta $A B C$ o bokach długości $a = |B C|$ , $b = |A C|$ , $c = |A B|$ .

Rozwiązanie

Przypomnijmy na początek, że dwusieczną trójkąta nazywamy odcinek, którego jednym z końców jest wierzchołek trójkąta, a drugim punkt przecięcia dwusiecznej kąta wewnętrznego przy tym wierzchołku z przeciwległym bokiem. Oznaczmy $|A D| = d_{α}$ .

RImH49bouCS1m

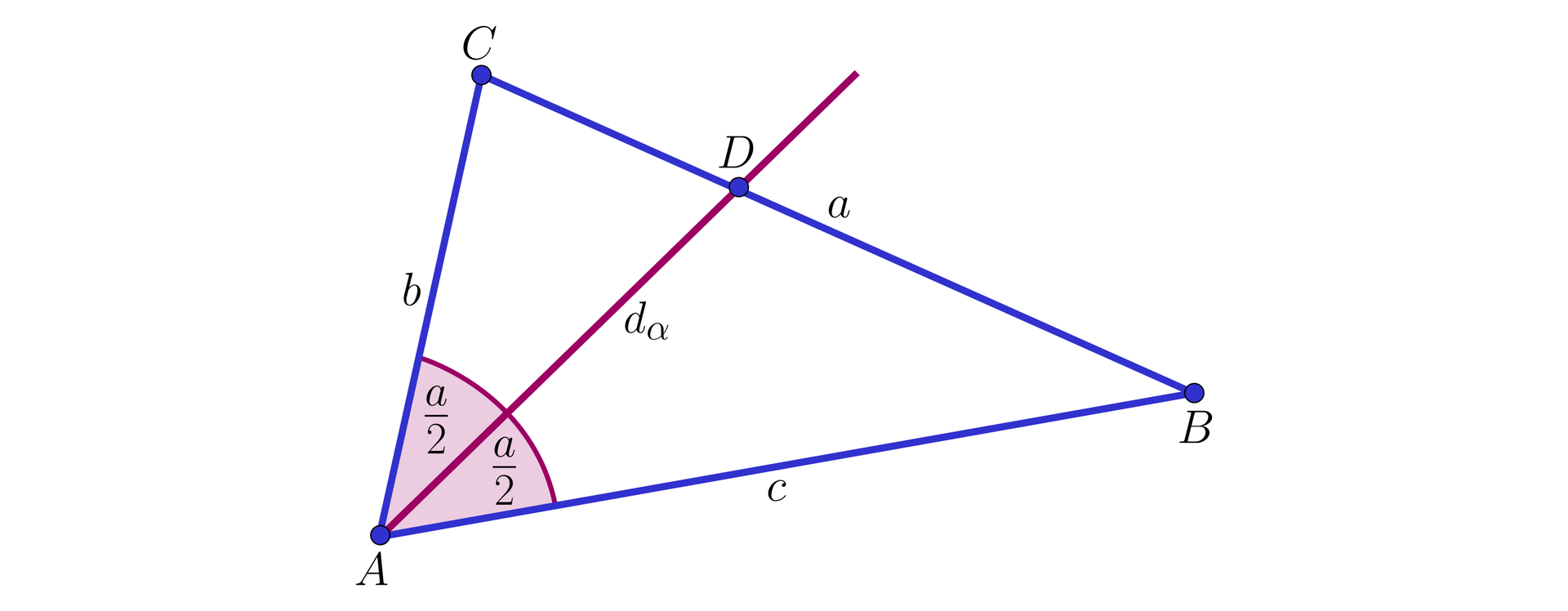
Ilustracja przedstawia trójkąt A B C. Bok AB ma miarę c, bok AC ma miarę B, a bok BC ma miarę a. Z punktu a poprowadzono dwusieczną podpisaną d indeks dolny alfa koniec indeksu na bok BC. Tworzy się tam punkt D dzielący bok BC na pół. Utworzyły się dwa trójkąty. Kąt przy wierzchołku A ma miarę alfa.

W pierwszym etapie rozwiązania wyznaczymy długości odcinków $B D$ i $C D$ w zależności od długości boków trójkąta. Niech $|B D| = x$ . Wtedy $|C D| = a - x$ .

R15Lod0dd00CQ

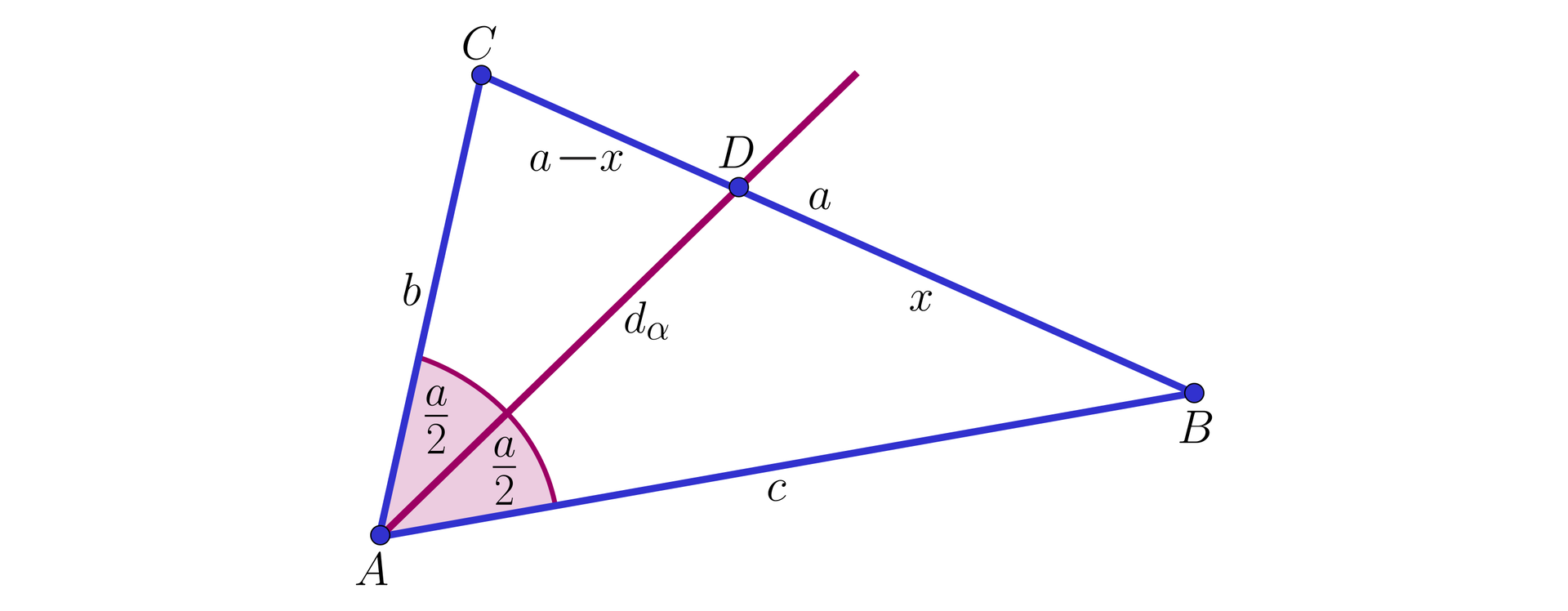
Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta mamy $\frac{|C D|}{|A C|} = \frac{|B D|}{|A B|}$ , czyli $\frac{a - x}{b} = \frac{x}{c}$ . Stąd $b x = a c - c x$ , więc $b x + c x = a c$ . Zatem $(b + c) x = a c$ , skąd $x = \frac{a c}{b + c}$ , czyli $|B D| = \frac{a c}{b + c}$ . Wobec tego $|C D| = a - x = a - \frac{a c}{b + c} = \frac{a b}{b + c}$ .

Drugi etap dowodu przeprowadzimy dwoma sposobami, analogicznymi do sposobów omówionych w Przykładzie 1.

$I$ sposób:
Zastosujmy twierdzenie cosinusów dla kąta $β$ w trójkątach $A B C$ i $A B D$ .
RiHzHPjX65DK1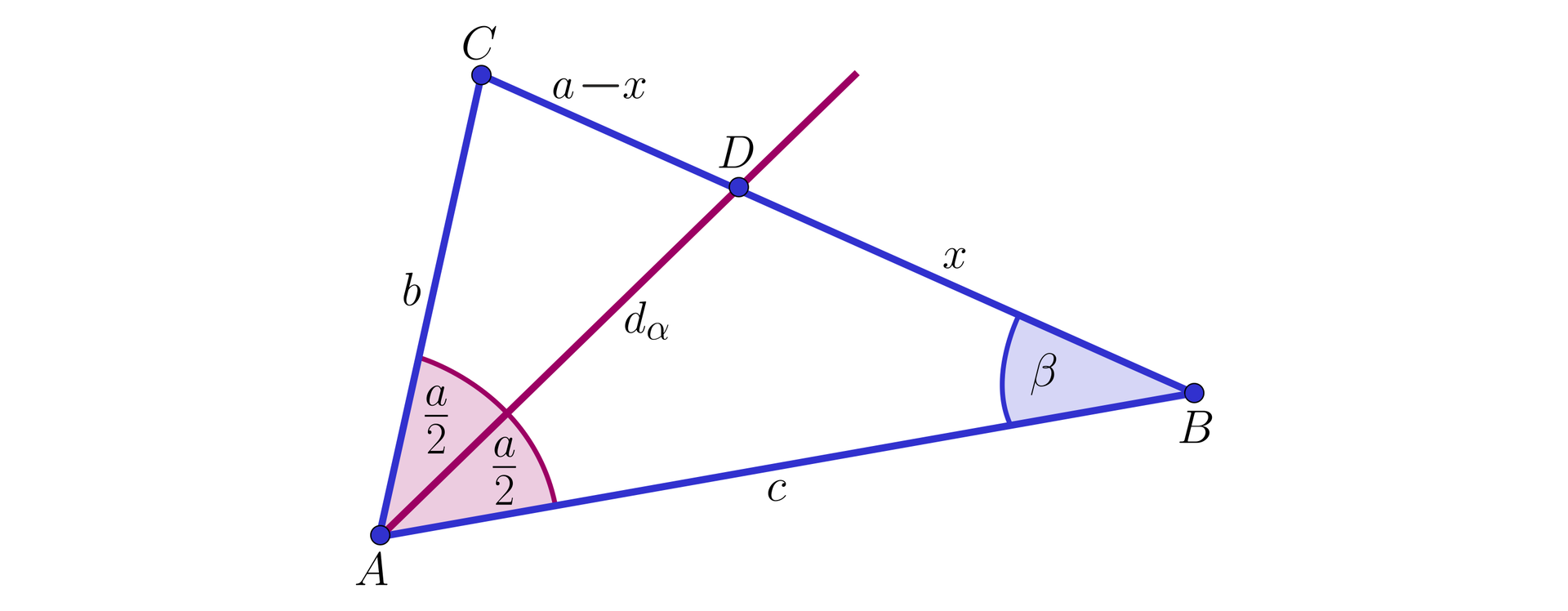
Ilustracja przedstawia trójkąt A B C. Bok AB ma miarę c, bok AC ma miarę B, a bok BC ma miarę a. Z punktu a poprowadzono dwusieczną podpisaną d indeks dolny alfa koniec indeksu na bok BC. Tworzy się tam punkt D dzielący bok BC na pół. Utworzyły się dwa trójkąty. Kąt przy wierzchołku A ma miarę alfa. Bok CD ma miarę $a - x$ a bok BD ma miarę x. Kąt przy wierzchołku B ma miarę beta.
Otrzymujmy w ten sposób układ równań
$b^{2} = a^{2} + c^{2} - 2 a c \cos β$ oraz $d_{α}^{2} = x^{2} + c^{2} - 2 \cdot x c \cos β$
z niewiadomymi $d_{α}$ , $x$ i $\cos β$ . Z poprzedniej części dowodu mamy jednak $x = \frac{a c}{b + c}$ , więc otrzymujemy układ równań
$b^{2} = a^{2} + c^{2} - 2 a c \cos β$ oraz $d_{α}^{2} = {(\frac{a c}{b + c})}^{2} + c^{2} - 2 \cdot \frac{a c}{b + c} \cdot c \cos β$
z dwiema niewiadomymi $d_{α}$ i $\cos β$ . Z pierwszego równania wyznaczamy $\cos β = \frac{a^{2} + c^{2} - b^{2}}{2 a c}$ (możemy też wyznaczyć $2 a c \cos β = a^{2} + c^{2} - b^{2}$ ). Stąd i z drugiego równania dostajemy
$d_{α}^{2} = {(\frac{a c}{b + c})}^{2} + c^{2} - 2 \cdot \frac{a c}{b + c} \cdot c \cdot \frac{a^{2} + c^{2} - b^{2}}{2 a c}$ .
Pozostaje tylko doprowadzić ten wynik do prostszej postaci.
$d_{α}^{2} = \frac{a^{2} c^{2}}{{(b + c)}^{2}} + c^{2} - c \cdot \frac{a^{2} + c^{2} - b^{2}}{b + c} =$
$= \frac{c}{{(b + c)}^{2}} (a^{2} c + c {(b + c)}^{2} - (b + c) (a^{2} + c^{2} - b^{2})) =$
$= \frac{c}{{(b + c)}^{2}} (a^{2} c + (b + c) (c (b + c) - (a^{2} + c^{2} - b^{2}))) =$
$= \frac{c}{{(b + c)}^{2}} (a^{2} c + (b + c) (b c - a^{2} + b^{2})) =$
$= \frac{c}{{(b + c)}^{2}} (a^{2} c + b^{2} c - a^{2} b + b^{3} + b c^{2} - a^{2} c + b^{2} c) =$
$= \frac{c}{{(b + c)}^{2}} (b^{2} c - a^{2} b + b^{3} + b c^{2} + b^{2} c) = \frac{b c}{{(b + c)}^{2}} (b^{2} + 2 b c + c^{2} - a^{2}) =$
$= \frac{b c}{{(b + c)}^{2}} ({(b + c)}^{2} - a^{2})$
Zatem $d_{α} = \frac{\sqrt{b c ({(b + c)}^{2} - a^{2})}}{b + c}$ .

$II$ sposób:
Zastosujmy twierdzenie cosinusów dla kątów $φ$ i $180 ° - φ$ w trójkątach $A C D$ i $A B D$ .
RnIum2GeliPKa
Ilustracja przedstawia trójkąt A B C. Bok AB ma miarę c, bok AC ma miarę B, a bok BC ma miarę a. Z punktu a poprowadzono dwusieczną podpisaną d indeks dolny alfa koniec indeksu na bok BC. Tworzy się tam punkt D dzielący bok BC na pół. Utworzyły się dwa trójkąty. Kąt przy wierzchołku A ma miarę alfa. W trójkącie ACD kąt przy wierzchołku D ma miarę $φ$ , w trójkącie ABD kąt przy wierzchołku D ma miarę $180 ° - φ$
Otrzymujemy w ten sposób układ równań
$b^{2} = d_{α}^{2} + {|C D|}^{2} - 2 d_{α} \cdot |C D| \cos φ$ oraz $c^{2} = d_{α}^{2} + {|B D|}^{2} - 2 d_{α} \cdot |B D| \cos (180 ° - φ)$ .
Stosując wzór redukcyjny $\cos (180 ° - φ) = - \cos φ$ , możemy ten układ zapisać w postaci
$b^{2} = d_{α}^{2} + {|C D|}^{2} - 2 d_{α} \cdot |C D| \cos φ$ oraz $c^{2} = d_{α}^{2} + {|B D|}^{2} + 2 d_{α} \cdot |B D| \cos φ$ .
Mnożąc obie strony pierwszego równania przez $|B D|$ , a drugiego przez $|C D|$ , otrzymujemy
$|B D| \cdot b^{2} = |B D| \cdot d_{α}^{2} + |B D| \cdot {|C D|}^{2} - 2 d_{α} \cdot |B D| \cdot |C D| \cos φ$
oraz
$|C D| \cdot c^{2} = |C D| \cdot d_{α}^{2} + |C D| \cdot {|B D|}^{2} + 2 d_{α} \cdot |C D| \cdot |B D| \cos φ$ .
Dodając stronami, dostajemy kolejno:
$|B D| \cdot b^{2} + |C D| \cdot c^{2} = |B D| \cdot d_{α}^{2} + |C D| \cdot d_{α}^{2} + |B D| \cdot {|C D|}^{2} + |C D| \cdot {|B D|}^{2}$ ,
$|B D| \cdot b^{2} + |C D| \cdot c^{2} = (|B D| + |C D|) \cdot d_{α}^{2} + |B D| \cdot |C D| \cdot (|B D| + |C D|)$ .
Ponieważ $|B D| + |C D| = a$ oraz $|B D| = \frac{a c}{b + c}$ i $|C D| = \frac{a b}{b + c}$ , co wykazaliśmy w pierwszym etapie rozwiązania, więc równanie to możemy zapisać w postaci
$\frac{a c}{b + c} \cdot b^{2} + \frac{a b}{b + c} \cdot c^{2} = a \cdot d_{α}^{2} + \frac{a c}{b + c} \cdot \frac{a b}{b + c} \cdot a$ .
Dzieląc obie strony równania przez $a$ , otrzymujemy kolejno
$\frac{c}{b + c} \cdot b^{2} + \frac{b}{b + c} \cdot c^{2} = d_{α}^{2} + \frac{a c}{b + c} \cdot \frac{a b}{b + c}$ ,
$\frac{b^{2} c + b c^{2}}{b + c} = d_{α}^{2} + \frac{a^{2} b c}{{(b + c)}^{2}}$ ,
$d_{α}^{2} = \frac{b^{2} c + b c^{2}}{b + c} - \frac{a^{2} b c}{{(b + c)}^{2}}$ ,
$d_{α}^{2} = \frac{b c (b + c)}{b + c} - \frac{a^{2} b c}{{(b + c)}^{2}}$ ,
$d_{α}^{2} = \frac{b c ({(b + c)}^{2} - a^{2})}{{(b + c)}^{2}}$ .
Zatem $d_{α} = \frac{\sqrt{b c ({(b + c)}^{2} - a^{2})}}{b + c}$ .

Zarówno w przypadku wyprowadzenia wzoru na długość środkowej trójkąta, jak i wzoru na długość dwusiecznej trójkąta korzystaliśmy dwukrotnie z twierdzenia cosinusów w dwóch trójkątach, przy czym twierdzenie to stosowaliśmy dla tego samego kąta lub dla kątów, które sumowały się do $180 °$ . Warto tę technikę zapamiętać.

Środkowa trójkąta oraz dwusieczna trójkąta to szczególne przypadki odcinka, którego jednym z końców jest wierzchołek trójkąta, a drugim punkt leżący na przeciwległym boku. Okazuje się, że istnieje zależność między długością takiego odcinka, a długościami odcinków powstałych na boku trójkąta i długościami boków trójkąta. Zależność ta została podana i udowodniona przez szkockiego matematyka Matthew Stewarta. Sformułujemy i udowodnimy tą zależność.

Stewarta

Twierdzenie: Stewarta

Punkt $D$ leży na boku $A B$ trójkąta $A B C$ oraz $|A B| = c$ , $|B C| = a$ , $|A C| = b$ , $|C D| = d$ , $|A D| = x$ , $|B D| = y$ , jak na rysunku.

R14Mo2vte6hhT

Ilustracja przedstawia trójkąt ABC. Bok AB ma miarę c, bok AC ma miarę B, a bok BC ma miarę a. Z wierzchołka C poprowadzono prostą d na bok AB tworząc punkt D dzielący bok na dwie długości x oraz y.

Wtedy prawdziwa jest równość:

a^{2} x + b^{2} y = d^{2} c + c x y

Dowód

Niech $φ = |∢ A D C|$ . Wtedy $|∢ B D C| = 180 ° - φ$ .

R1NXutYNB2TaS

Z twierdzenia cosinusów dla kątów $φ$ i $180 ° - φ$ w trójkątach $A D C$ i $B C D$ otrzymujemy układ równań
$b^{2} = d^{2} + x^{2} - 2 d x \cos φ$ oraz $a^{2} = d^{2} + y^{2} - 2 d y \cos (180 ° - φ)$ .
Ponieważ $\cos (180 ° - φ) = - \cos φ$ , więc możemy ten układ zapisać w postaci
$b^{2} = d^{2} + x^{2} - 2 d x \cos φ$ oraz $a^{2} = d^{2} + y^{2} + 2 d y \cos φ$ .
Mnożąc obie strony pierwszego równania przez $y$ , a drugiego przez $x$ , otrzymujemy
$b^{2} y = d^{2} y + x^{2} y - 2 d x y \cos φ$ oraz $a^{2} x = d^{2} x + x y^{2} + 2 d x y \cos φ$ .
Stąd, po zsumowaniu stron tych równań, dostajemy kolejno:
$a^{2} x + b^{2} y = d^{2} x + d^{2} y + x^{2} y + x y^{2}$ ,
$a^{2} x + b^{2} y = d^{2} (x + y) + (x + y) x y$ .
Ponieważ $x + y = c$ , więc otrzymujemy
$a^{2} x + b^{2} y = d^{2} c + c x y$ .
To kończy dowód.

Znajomość tego twierdzenia oraz umiejętność jego zastosowania nie jest objęta wymaganiami podstawy programowej, warto jednak je pamiętać, gdyż pozwala znacznie skrócić rozwiązanie problemu w niektórych sytuacjach.

Słownik

wzór na długość środkowej trójkąta

długość środkowej trójkąta o bokach długości $a$ , $b$ , $c$ poprowadzonej do boku o długości $a$ jest równa:

m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}

wzór na długość dwusiecznej trójkąta

długość dwusiecznej trójkąta o bokach długości $a$ , $b$ , $c$ poprowadzonej do boku o długości $a$ jest równa:

d_{α} = \frac{\sqrt{b c ({(b + c)}^{2} - a^{2})}}{b + c}

Wprowadzenie

Animacja

Słownik