Przeczytaj

Wielokąty gwiaździste

Wiadomo, że wszystkie wielokąty foremne o takiej samej liczbie boków są podobne. Ale już wielokąty foremne gwiaździstewielokąt foremny gwiaździstywielokąty foremne gwiaździste o takiej samej liczbie boków nie muszą być figurami geometrycznymi podobnymi. Okazuje się, że istnieje tyle różnych (tzn. niepodobnych) $n$ -kątów foremnych gwiaździstych, ile jest liczb naturalnych względnie pierwszych z $n$ , z przedziału $(1, \frac{n}{2})$ . Dla $n = 7$ istnieją dwie takie liczby, które są względnie pierwsze z liczbą $7$ i które należą do zbioru $(1, \frac{7}{2})$ - są to liczby $2$ i $3$ . Oczekujemy zatem, że dla danego siedmiokąta foremnego, będą dwa różne siedmiokąty foremne gwiaździste. Poniższe rysunki pokazują, że rzeczywiście tak jest.

RPVdNlupuF4ju

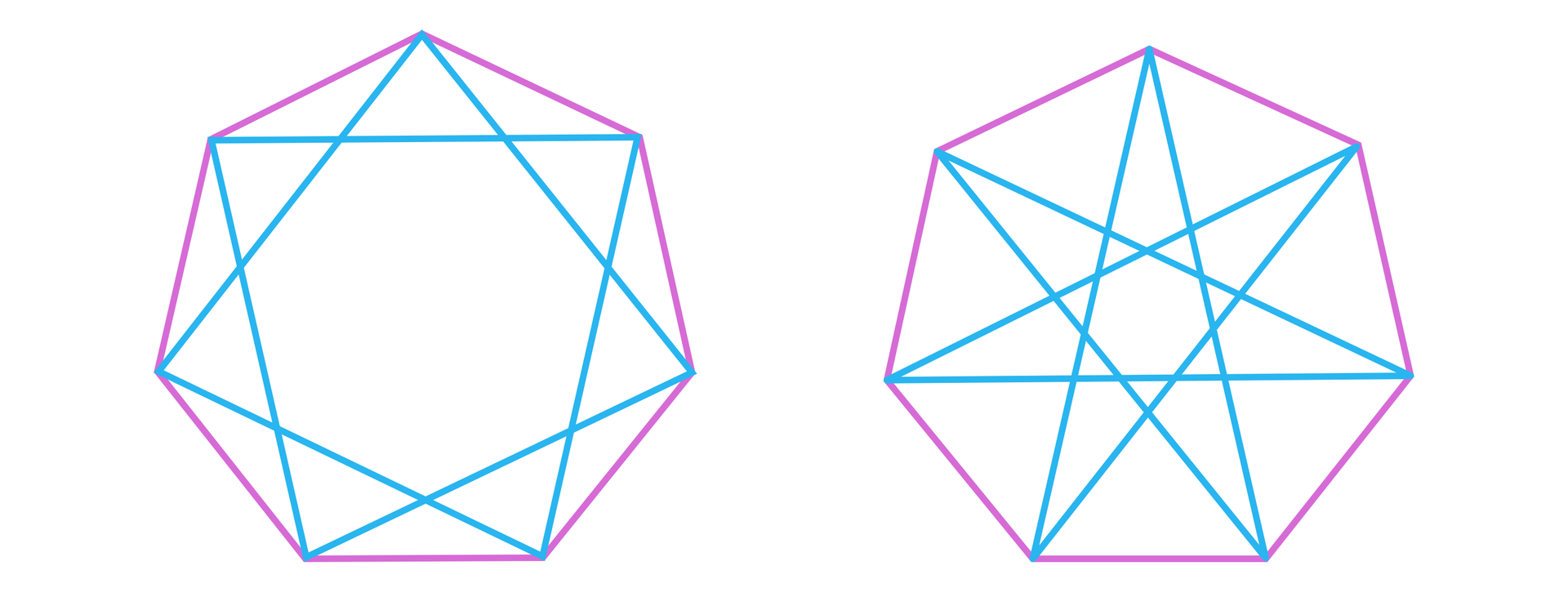
Ilustracja przedstawia dwie figury ustawione obok siebie. Z lewej mamy siedmiokąt gwiaździsty, czyli siedmiokąt foremny, którego boki są jednocześnie podstawami identycznych trójkątów równoramiennych. Wierzchołki łączące ramiona tych trójkątów połączono odcinkami i utworzono drugi, większy siedmiokąt foremny. Analogiczna jest konstrukcja po prawej, przy czym kąt przy wierzchołku łączącym ramiona trójkątów w lewej figurze jest większy, niż w kąt z figurze po prawej, zatem siedmiokąt po lewej ma bardziej szpiczaste kąty sterczące. — siedmiokąt gwiaździsty $\{7 / 2\}$ oraz siedmiokąt gwiaździsty $\{7 / 3\}$

Sposób konstrukcji takich dwóch siedmiokątów wynika z metody Brożka. Mamy, że $7 = 1 + 6 = 2 + 5 = 3 + 4$ . Pierwszy rozkład na składniki „definiuje” siedmiokąt foremny, kolejny wskazuje na możliwość łączenia co drugiego z wierzchołków siedmiokąta, a ostatni pozwala skonstruować wielokąt gwiaździstywielokąt foremny gwiaździstywielokąt gwiaździsty, poprzez łączenie co trzeciego z wierzchołków siedmiokąta foremnego.

Przykład 1

Naszym celem będzie teraz skonstruowanie wielokątów foremnych gwiaździstych utworzonych z przekątnych danego ośmiokąta foremnego.

Wyznaczymy najpierw liczbę takich figur. W przedziale $(1, \frac{8}{2})$ , są dwie liczby naturalne: $2$ i $3$ . Liczba $2$ nie jest względnie pierwsza z liczbą $8$ , ale liczba $3$ jest względnie pierwsza z liczbą $8$ . Wiemy więc, że jest jeden ośmiokąt foremny gwiaździsty.

Korzystając z metody Brożka możemy zapisać, że $8 = 1 + 7 = 2 + 6 = 3 + 5 = 4 + 4$ . Pierwszy z rozkładów na składniki opisuje ośmiokąt foremny. Rozkład $8 = 2 + 6$ , wyznaczony przez liczbę $2$ , która nie jest względnie pierwsza z liczbą $8$ , prowadzi do „zamknięcia” łamanej zanim dotrze ona do każdego z wierzchołków.

RvNXeufyanLGQ

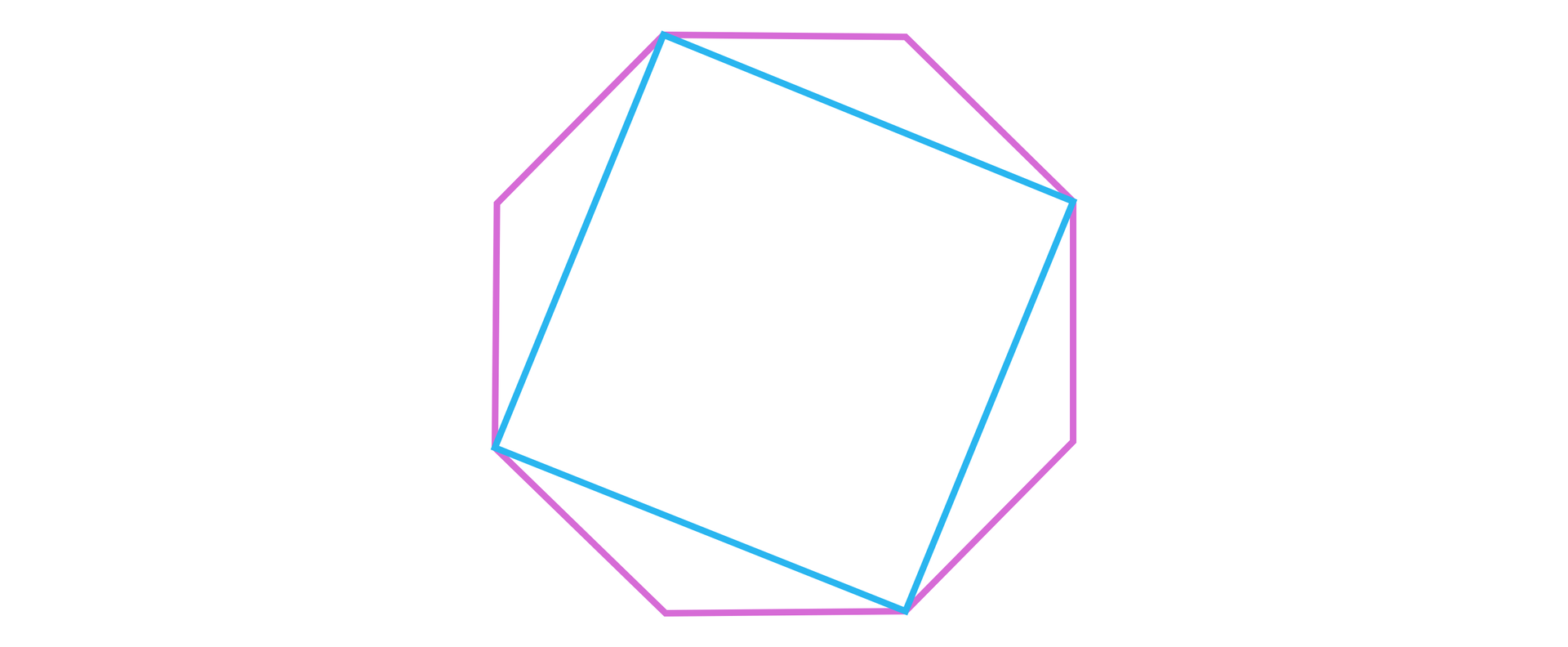
Ilustracja przedstawia łamaną zamkniętą rozpiętą na czterech wierzchołkach ośmiokąta tak, że wierzchołki łamanej pokrywają się z co drugim wierzchołkiem ośmiokąta. Łamana przyjmuje postać kwadratu. — łamana zamknięta w ośmiokącie

Okaże się, że rozkład $8 = 3 + 5$ , wyznaczony przez liczbę $3$ , która jest względnie pierwsza z liczbą $8$ , prowadzi do skonstruowania ośmiokąta gwiaździstego.

Rx0kDdEo4fsQa

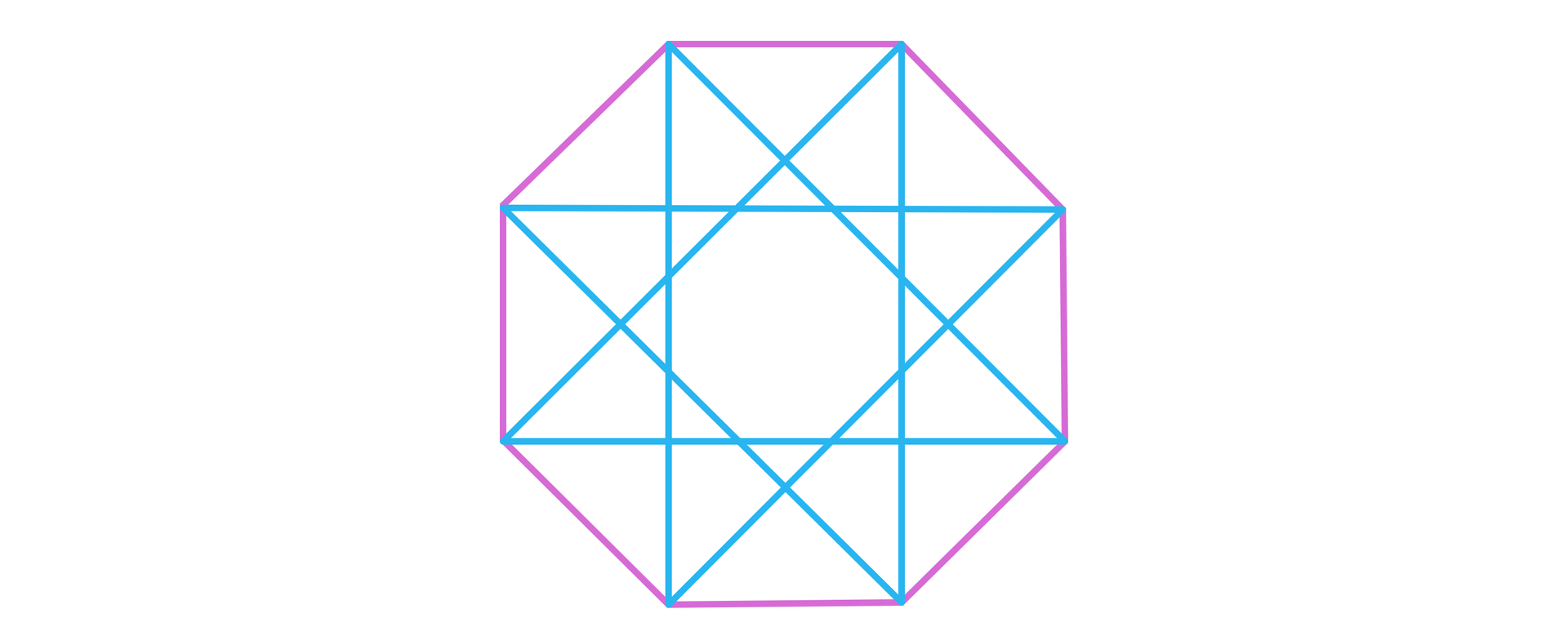
Ilustracja przedstawia ośmiokąt foremny, w który wpisany jest ośmiokąt foremny gwiaździsty. — ośmiokąt foremny gwiaździsty

Pozostaje dodać, że rozkład $8 = 4 + 4$ prowadzi w oczywisty sposób do konstrukcji odcinka.

O konstrukcjach wielokątów foremnych i liczbach względnie pierwszych raz jeszcze

Jak zauważyliśmy w poprzednim akapicie, liczba wielokątów foremnych gwiaździstychwielokąt foremny gwiaździstywielokątów foremnych gwiaździstych jest ściśle związana z występowaniem liczb, które są względnie pierwszeliczby względnie pierwszewzględnie pierwsze z liczbą opisującą ilość boków danego wielokąta. Pamiętamy także o kryterium Gaussa, które orzeka o możliwości skonstruowania wielokąta foremnego za pomocą klasycznych metod, tj. tylko za pomocą cyrkla i linijki. Gauss stwierdził, że $n$ -kąt foremny można skonstruować tylko wtedy, gdy $n = 2^{m} \cdot p_{1} \cdot p_{2} \cdot . . . \cdot p_{k}$ , gdzie $m$ jest liczbą naturalną (wraz z zerem), a $p_{i}$ są różnymi pierwszymi liczbami Fermata lub gdy $n = 2^{m}$ , gdzie $m$ jest liczbą naturalną nie mniejszą niż 2. Przypomnijmy jeszcze, że liczbą Fermata jest liczba postaci $F_{k} = 2^{2^{k}} + 1$ , gdzie $k$ jest nieujemną liczbą całkowitą. Każdy z nas potrafi skonstruować trójkąt równoboczny, czyli trójkąt foremny. Niemal każdy wie, że da się skonstruować pięciokąt foremny, a opis tej konstrukcji łatwo znaleźć. Okazuje się, że to nam wystarcza, by stwierdzić, że możliwe jest skonstruowanie $15$ -kąta foremnego. Mówi o tym poniższe twierdzenie.

o konstrukcji wielokąta foremnego i liczbach względnie pierwszych

Twierdzenie: o konstrukcji wielokąta foremnego i liczbach względnie pierwszych

Jeśli liczby $m$ i $n$ są względnie pierwsze oraz $m$ -kąt foremny i $n$ -kąt foremny można skonstruować metodami klasycznymi, to można też skonstruować wielokąt foremny, którego liczba boków jest iloczynem $m \cdot n$ .

Dowód

Skorzystamy z kryterium Gaussa.

Przypuśćmy, że jedna z liczb, np. liczba $m$ , jest postaci $2^{p}$ , gdzie $p$ jest liczbą naturalną nie mniejszą niż $2$ . Wtedy, z faktu, że liczby $m$ , $n$ są względnie pierwszeliczby względnie pierwszewzględnie pierwsze wynika, że liczba $n$ nie może dzielić się przez $2$ – jest zatem postaci $2^{l} \cdot p_{1} \cdot p_{2} \cdot \dots \cdot p_{k}$ , gdzie musi być $l = 0$ . Zauważmy jednak, że wówczas $m \cdot n = 2^{p} \cdot 2^{0} \cdot p_{1} \cdot p_{2} \cdot \dots \cdot p_{k} = 2^{p} \cdot p_{1} \cdot p_{2} \cdot \dots \cdot p_{k}$ . Jest to zatem postać, która wskazuje, na mocy kryterium Gaussa, że da się skonstruować wielokąt foremny o takiej liczbie boków.

Przypuśćmy teraz, że $m = 2^{0} \cdot p_{1} \cdot p_{2} \cdot \dots \cdot p_{k}$ oraz $n = 2^{0} \cdot q_{1} \cdot q_{2} \cdot \dots \cdot q_{k}$ . Wtedy z faktu, że liczby $m$ , $n$ są względnie pierwsze wynika, że żadna z liczb $p_{i}$ nie może być równa jakiejkolwiek z liczb $q_{j}$ . Ale wówczas iloczyn $m \cdot n$ jest równy $p_{1} \cdot p_{2} \cdot \dots \cdot p_{k} \cdot q_{1} \cdot q_{2} \cdot \dots \cdot q_{l}$ , czyli jest postaci $2^{0} \cdot p_{1} \cdot p_{2} \cdot \dots \cdot p_{k} \cdot q_{1} \cdot q_{2} \cdot \dots \cdot q_{l}$ . Jest to zatem postać, która wskazuje, na mocy kryterium Gaussa, że da się skonstruować wielokąt foremny o takiej liczbie boków. Co należało wykazać.

Wracając do $15$ -kąta foremnego możemy stwierdzić, że z faktu, że liczby $3$ i $5$ są względnie pierwszeliczby względnie pierwszewzględnie pierwsze i $15 = 3 \cdot 5$ wynika (po skorzystaniu z powyższego twierdzenia), że $15$ -kąt foremny da się skonstruować za mocą metod klasycznych. Wcześniej musielibyśmy zapisać, że $15 = (2^{2^{0}} + 1) \cdot (2^{2^{1}} + 1)$ , czyli zapisać liczbę $15$ w postaci iloczynu liczb pierwszych Fermata.

Ciekawostka

promień okręgu wpisanego w wielokąt foremny nazywamy apotemą wielokąta foremnego

Słownik

wielokąt foremny gwiaździsty

$n$ -kątem foremnym gwiaździstym nazywamy łamaną zamkniętą o $n$ wierzchołkach, utworzoną z tych przekątnych $n$ -kąta foremnego, które mają równą długość

liczby względnie pierwsze

powiemy, że dwie liczby całkowite są względnie pierwsze, jeśli ich największym wspólnym dzielnikiem jest liczba $1$

Wprowadzenie

Gra edukacyjna

Wielokąty gwiaździste

O konstrukcjach wielokątów foremnych i liczbach względnie pierwszych raz jeszcze

Słownik