Przeczytaj
Na początku przedstawimy modele obliczania długości trzeciego boku trójkąta przy danych dwóch bokach oraz jednym kącie tego trójkąta.
Rozwiązywanie trójkątów (model 1)
Obliczanie długości trzeciego boku trójkąta, gdy dane są:
długości dwóch boków tego trójkąta oraz
kąt między tymi bokami.
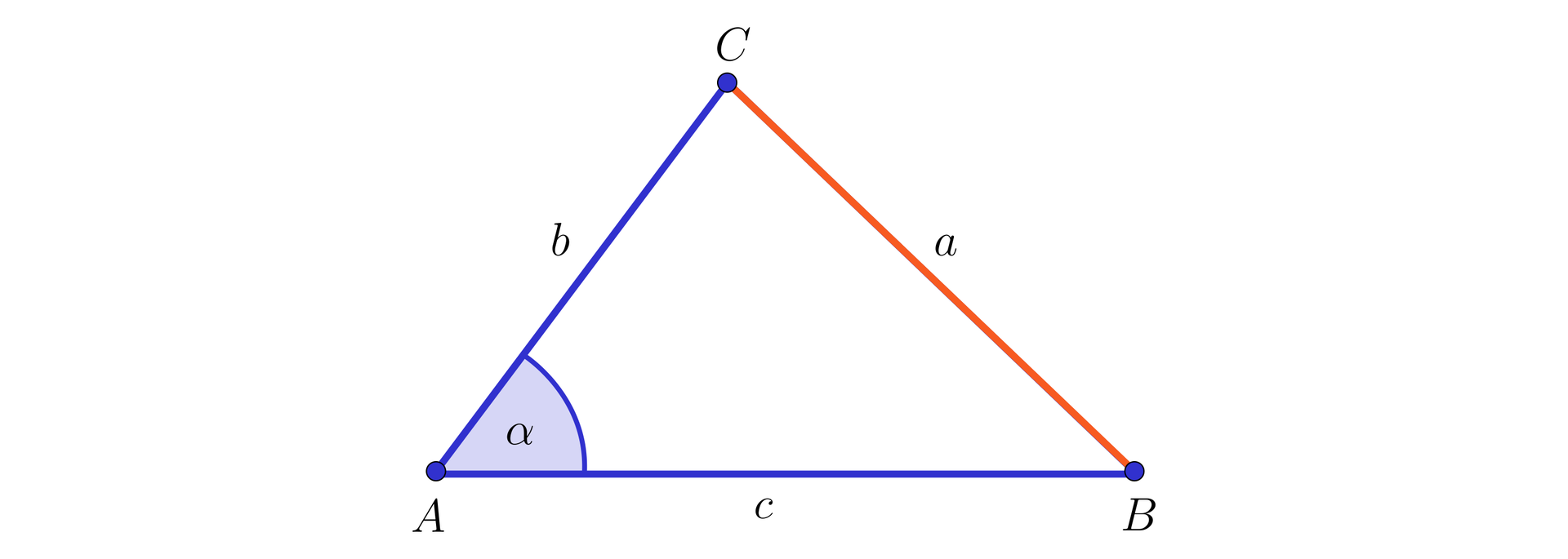
Z twierdzenia cosinusów dla boku i kąta otrzymujemy:
Stąd:
W tym przypadku otrzymujemy jedną wartość .
Rozwiązywanie trójkątów (model 2)
Obliczanie długości trzeciego boku trójkąta, gdy dane są:
długości dwóch boków tego trójkąta oraz
kąt między jednym z tych boków i bokiem szukanym.
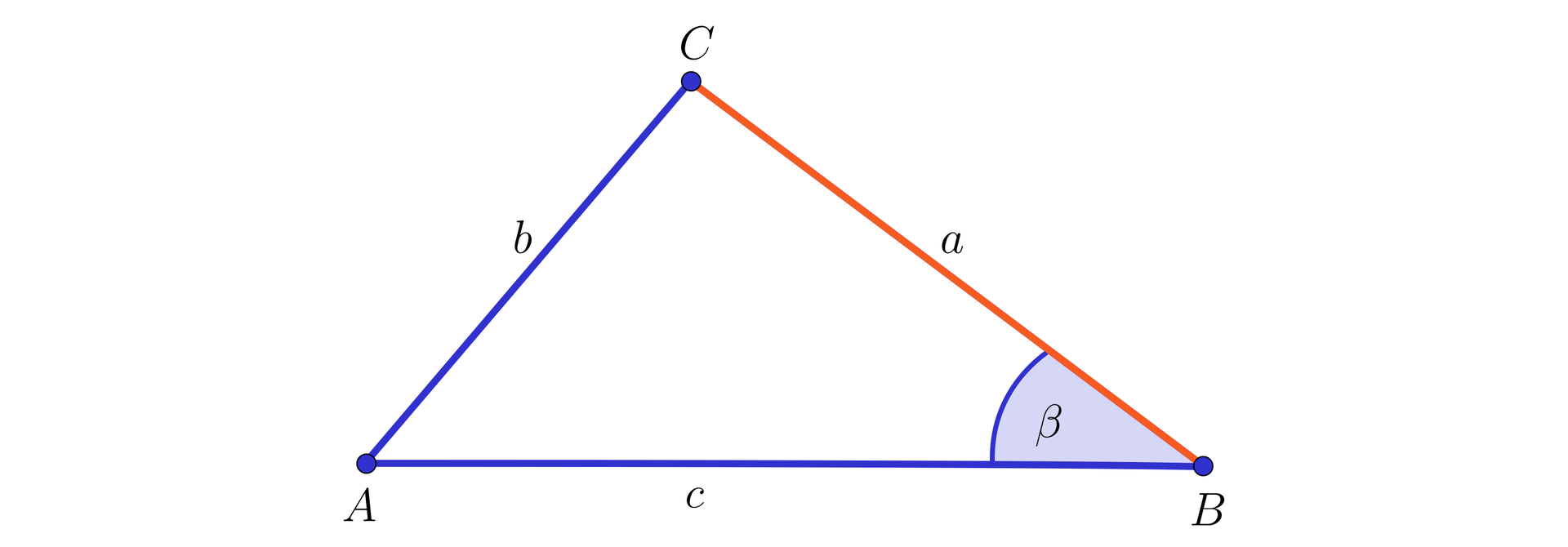
Krok 1.
Z twierdzenia cosinusów dla boku i kąta mamy:
Stąd otrzymujemy równanie kwadratowe:
Krok 2.
Obliczamy wyróżnik tego równania.
Krok 3.
Analizujemy rozwiązania tego równania.
Gdy równanie:
nie ma rozwiązań rzeczywistych (), to szukany trójkąt nie istnieje;
ma rozwiązania rzeczywiste , , ale żadne z nich nie jest dodatnie (; ; ), to szukany trójkąt nie istnieje;
ma dwa rozwiązania rzeczywiste , , z których tylko jedno jest dodatnie (; ; ), to istnieje tylko jeden taki trójkąt i szukany bok trójkąta ma wtedy długość ;
ma dokładnie jedno rozwiązanie i jest nim liczba dodatnia (; ), to istnieje tylko jeden taki trójkąt i szukany bok trójkąta ma wtedy długość ;
ma dwa rozwiązania rzeczywiste , i każde z nich jest dodatnie (; ; ), to istnieją dwa takie trójkąty, a szukany bok trójkąta ma wtedy długość lub .
Obliczymy długość boku trójkąta, w którym dane są: , oraz .
Rozwiązanie
Skorzystamy z modelu 1: .
Stąd:
.
Obliczymy długość boku trójkąta, w którym dane są: , oraz .
Rozwiązanie
Skorzystamy z modelu 2. Z twierdzenia cosinusów dla boku i kąta mamy:
Stąd otrzymujemy równanie kwadratowe:
Obliczamy wyróżnik otrzymanego równania kwadratowego:
Zatem taki trójkąt nie istnieje.
Obliczymy długość boku trójkąta, w którym dane są: , oraz .
Rozwiązanie
Skorzystamy z modelu 2. Z twierdzenia cosinusów dla boku i kąta mamy:
Stąd otrzymujemy równanie kwadratowe:
Obliczamy wyróżnik otrzymanego równania kwadratowego:
lub
Odpowiedź:
lub .
Obliczymy długość boku trójkąta, w którym dane są: , oraz
Rozwiązanie
Skorzystamy z modelu 2. Z twierdzenia cosinusów dla boku i kąta mamy:
Stąd otrzymujemy równanie kwadratowe:
Obliczamy wyróżnik otrzymanego równania kwadratowego:
lub
Odpowiedź
.
Dwa boki trójkąta mają długości i , a kąt między tymi bokami ma miarę . Obliczymy długość trzeciego boku.
Rozwiązanie
Skorzystamy z modelu . Z twierdzenia cosinusów otrzymujemy , gdzie oznacza długość trzeciego boku trójkąta. Zatem .
Pozostaje obliczyć . Możemy oczywiście odczytać przybliżoną wartość z tablic wartości funkcji trygonometrycznych, ale wtedy otrzymamy również przybliżoną wartość .
Obliczymy jednak dokładną wartość . Wartość tę można uzyskać na wiele sposobów.
Pokażemy cztery sposoby.
W pierwszym wykorzystamy tożsamość trygonometryczną – wzór na cosinus podwojonego kąta, w drugim – wzór na cosinus różnicy kątów. W trzecim i czwartym sposobie wykorzystamy jedynie geometrię.
Pierwszy sposób obliczenia wartości .
Wzór na cosinus podwojonego kąta ma postać .
Dla przybiera on postać , skąd .
Ponieważ , a kąt jest ostry, więc .
Drugi sposób obliczenia wartości .
Tym razem wykorzystamy wzór na cosinus różnicy kątów
.
Ponieważ , więc
Może nieco dziwić otrzymany wynik, gdyż na pierwszy rzut oka jest on inny niż uzyskany w pierwszym sposobie. Tak jednak nie jest. Wystarczy zauważyć, że
.
Trzeci sposób obliczenia wartości .
Narysujmy trójkąt prostokątny o kątach ostrych i .
Poprowadźmy też dwusiecznądwusieczną kąta .
Niech , i , jak na rysunku.
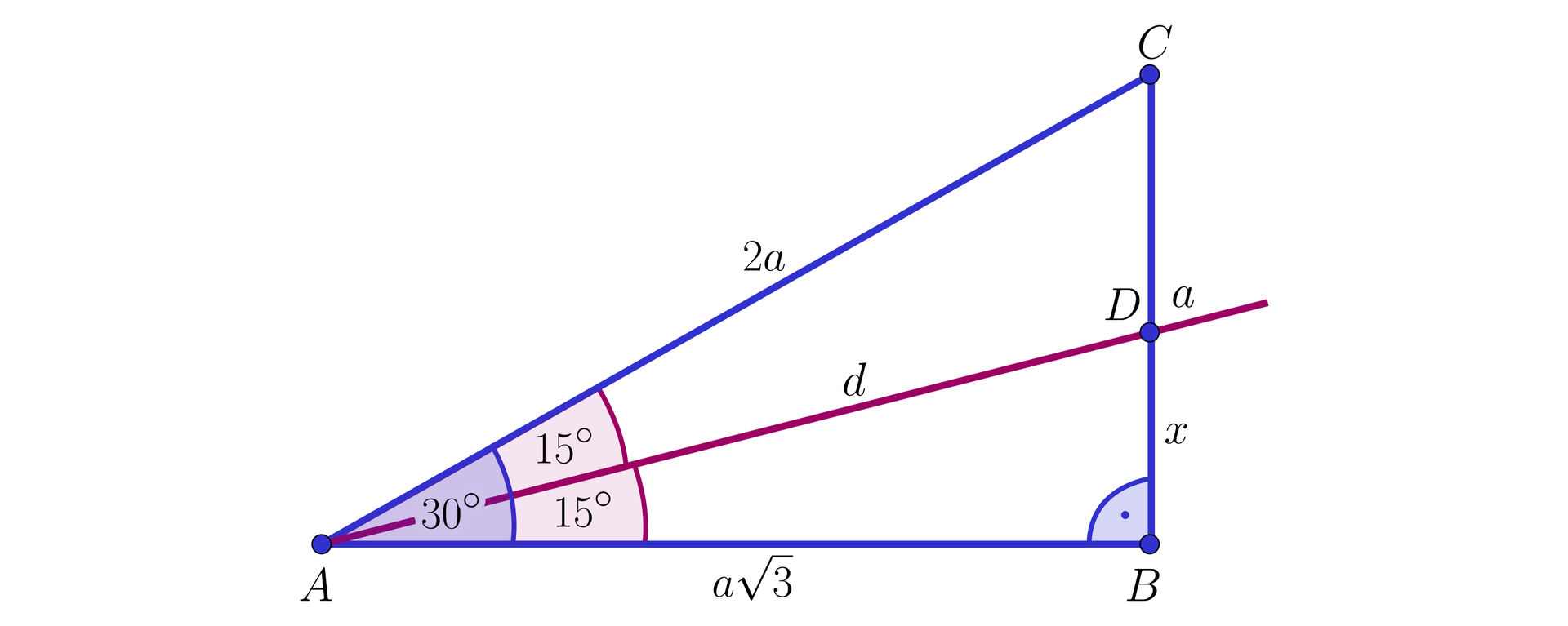
Wtedy oraz , więc . Z twierdzenia o dwusiecznej kąta wewnętrznego trójkąta otrzymujemy , czyli .
Stąd wyznaczamy kolejno , , .
Mnożąc obie strony tej równości przez otrzymujemy , czyli .
Z twierdzenia Pitagorasa dla trójkąta otrzymujemy . Stąd
.
Zatem z definicji cosinusa kąta ostrego w trójkącie prostokątnym otrzymujemy
.
Czwarty sposób obliczenia wartości .
Wewnątrz kwadratu o boku długości wybierzmy taki punkt , żeby trójkąt był równoboczny.
Poprowadźmy też przez punkt odcinek równoległy do boku kwadratu tak, jak na rysunku.

Ponieważ trójkąt jest równoboczny, więc i .
To oznacza, że trójkąt jest równoramienny, a jego kąt przy podstawie jest równy .
To z kolei oznacza, że .
Odcinek jest wysokością trójkąta równobocznego , więc , więc .
Punkt jest środkiem odcinka , więc .
Z twierdzenia Pitagorasa dla trójkąta otrzymujemy , czyli . Stąd
.
Zatem z definicji cosinusa kąta ostrego w trójkącie prostokątnym otrzymujemy
.
Powracamy do wyznaczenia długości trzeciego boku:
W trójkącie dane są długości boków i oraz , gdzie oznacza miarę kąta przy wierzchołku tego trójkąta. Obliczymy długość boku .
Rozwiązanie
Do obliczenia długości boku wykorzystamy twierdzenie cosinusów. Długości dwóch boków trójkąta znamy, więc potrzebna jest nam jeszcze wartość cosinusa kąta .
Tę wartość obliczymy, wykorzystując dwie znane tożsamości trygonometryczne
oraz .
Wstawiając w pierwszej z tych równości w miejsce otrzymujemy równanie , skąd .
Stąd i z drugiej tożsamości otrzymujemy
,
,
,
.
Stąd lub . Kąt jest rozwarty, gdyż . Zatem .
Teraz mamy już wszystkie dane, żeby obliczyć za pomocą twierdzenia cosinusów długość boku .
Otrzymujemy więc
,
.
Stąd .
Obliczymy miary kątów trójkąta o bokach długości: , , .
Rozwiązanie
Niech oznacza kąt trójkąta leżący naprzeciw boku o długości ,
– kąt leżący naprzeciw boku o długości ,
– kąt leżący naprzeciw boku o długości .
Zastosujmy twierdzenie cosinusów dla kąta .
,
,
,
.
Stąd
.
Zatem .
Zastosujmy jeszcze raz twierdzenie cosinusów dla kąta .
,
,
,
,
.
Stąd
.
Zatem .
Kąt obliczymy, korzystając z twierdzenia o sumie miar kątów wewnętrznych trójkąta, choć moglibyśmy ten kąt obliczyć, wykorzystując twierdzenie cosinusów. Mamy zatem:
.
Słownik
półprosta dzieląca kąt na dwa kąty przystające