Przeczytaj

Twierdzenie Weierstrassa

Szukanie wartości największych i najmniejszych różnych funkcji rozpoczniemy od zastanowienia się, czy na pewno istnieją. W tym celu zapoznajmy się z twierdzeniem Weierstrassa o osiąganiu kresów.

twierdzenie Weierstrassa

Twierdzenie: twierdzenie Weierstrassa

Niech $f$ będzie funkcją ciągłą, określoną na domkniętym przedziale $a \leq x \leq b$ . Istnieją takie argumenty $c$ i $d$ z przedziału $a \leq x \leq b$ , w których funkcja przyjmuje wartości ekstremalne, to znaczy dla każdego argumentu $x$ z przedziału $a \leq x \leq b$ mamy $f (c) \leq f (x) \leq f (d)$ .

Twierdzenie to mówi, że każda funkcja ciągła, określona na przedziale domkniętym, osiąga na tym przedziale wartość najmniejszą oraz największą. Nie tylko funkcje, spełniające założenia twierdzenia Weierstrassa (ciągłe, określone na przedziale domkniętym) mają taką własność, na przykład funkcja signum, wyznaczająca znak liczby,

sign (x) = \{\begin{cases} - 1 dla x < 0 \\ 0 dla x = 0 \\ 1 dla x > 0 \end{cases}

jest określona dla wszystkich liczb rzeczywistych, oraz nie jest ciągła (w zerze), a osiąga swoje kresy, i to wielokrotnie. Możemy na przykład przyjąć $c = - 3$ i $d = 12$ , i zobaczymy, że dla każdej wartości $x$ mamy $- 1 = f (c) \leq f (x) \leq f (d) = 1$ .

R2IynAW6AT93r

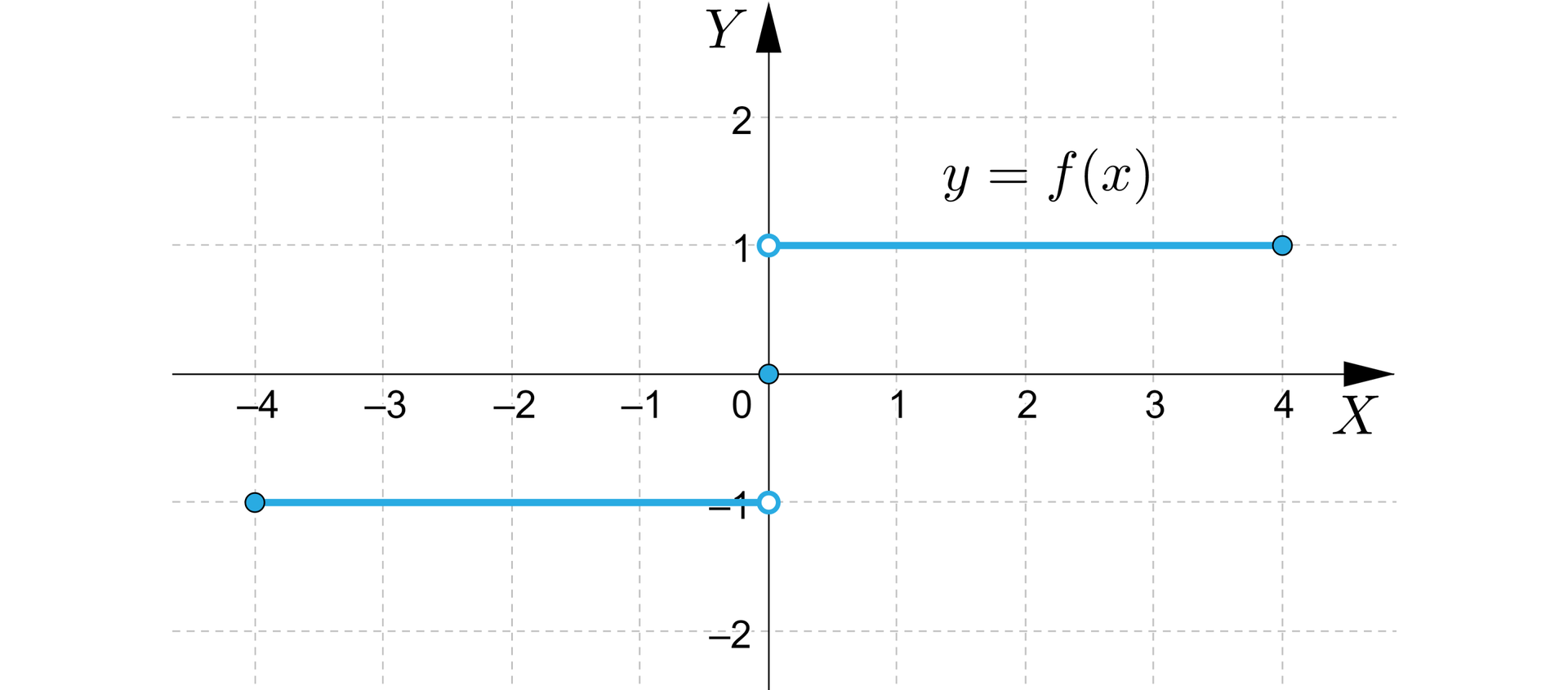
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz pionową osią Y od minus dwóch do dwóch. W układzie współrzędnych zaznaczono wykres funckji f , który składa się z dwóch poziomych odcinków oraz punktu. Pierwszy odcinek zaczyna się w zamalowanym punkcie o współrzędnych -4,-1 i łączy się z niezamalowanym punktem o współrzędnych 0,-1, drugi odcinek zaczyna się w niezamalowanym punkcie 0,1 i łączy się z punktem 4,1. Dodatkowo zaznaczony jest punkt o współrzędnych 0,<0. — Wykres funkcji nieciągłej, osiągającej swoje kresy

Jeżeli funkcja nie spełnia założeń twierdzenia Weierstrassa, to nie możemy jednak mieć pewności, czy osiąga swoje kresy. Funkcja ciągła, ale określona na zbiorze niedomkniętym, może nie osiągać swoich kresów. Weźmy funkcję $f (x) = 3 - x$ , zdefiniowaną na przedziale otwartym $0 < x < 2$ . Osiąga ona wartości pomiędzy $1$ i $3$ , i to dowolnie blisko liczb $1$ i $3$ , ale w żadnym punkcie swojej dziedziny nie przyjmuje wartości $1$ ani $3$ .

RXsGxn8NjjcPd

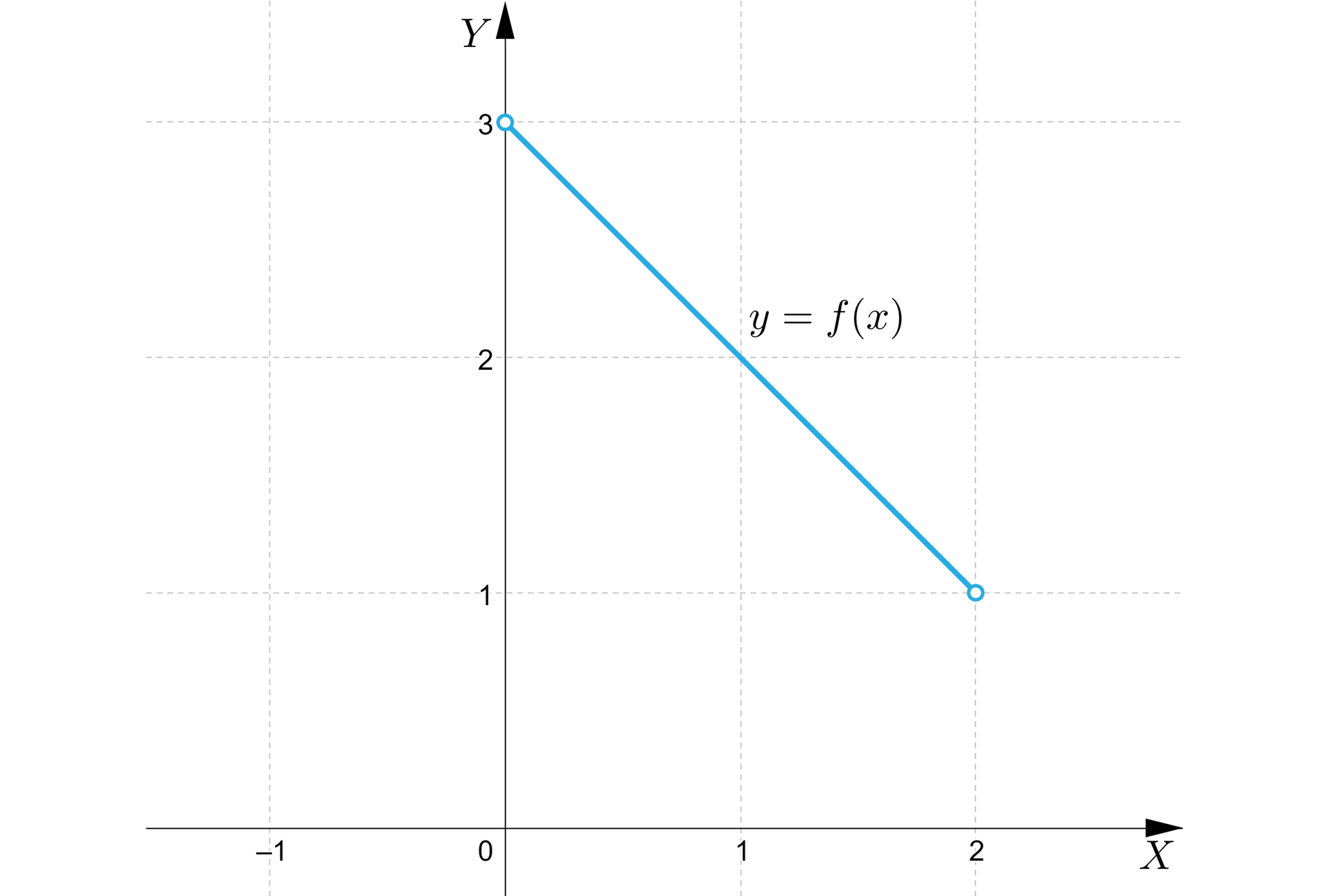
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do dwóch oraz pionową osią Y od zera do trzech. W układzie współrzędnych zaznaczono wykres funckji f , który składa się z odcinka, który zaczyna się w niezamalowanym punkcie 0,3 i łączy się z niezamalowanym punktem o współrzędnych 2,1. — Wykres funkcji na przedziale otwartym, nieosiągającej swoich kresów

Podobnie funkcja nieciągła, nawet określona na przedziale domkniętym, może nie osiągać swoich kresów. Obejrzyjmy funkcję

y = \{\begin{cases} \sqrt{1 - x^{2}} dla - 1 \leq x < 0 \\ 0 dla x = 0 \\ - \sqrt{1 - x^{2}} dla 0 < x \leq 1 \end{cases}

Przyjmuje ona wartości dowolnie bliskie $1$ , ale mniejsze od $1$ , i dowolnie bliskie $(- 1)$ , ale większe niż $(- 1)$ , nie osiąga więc swoich kresów.

RIWUmPQpE1EOb

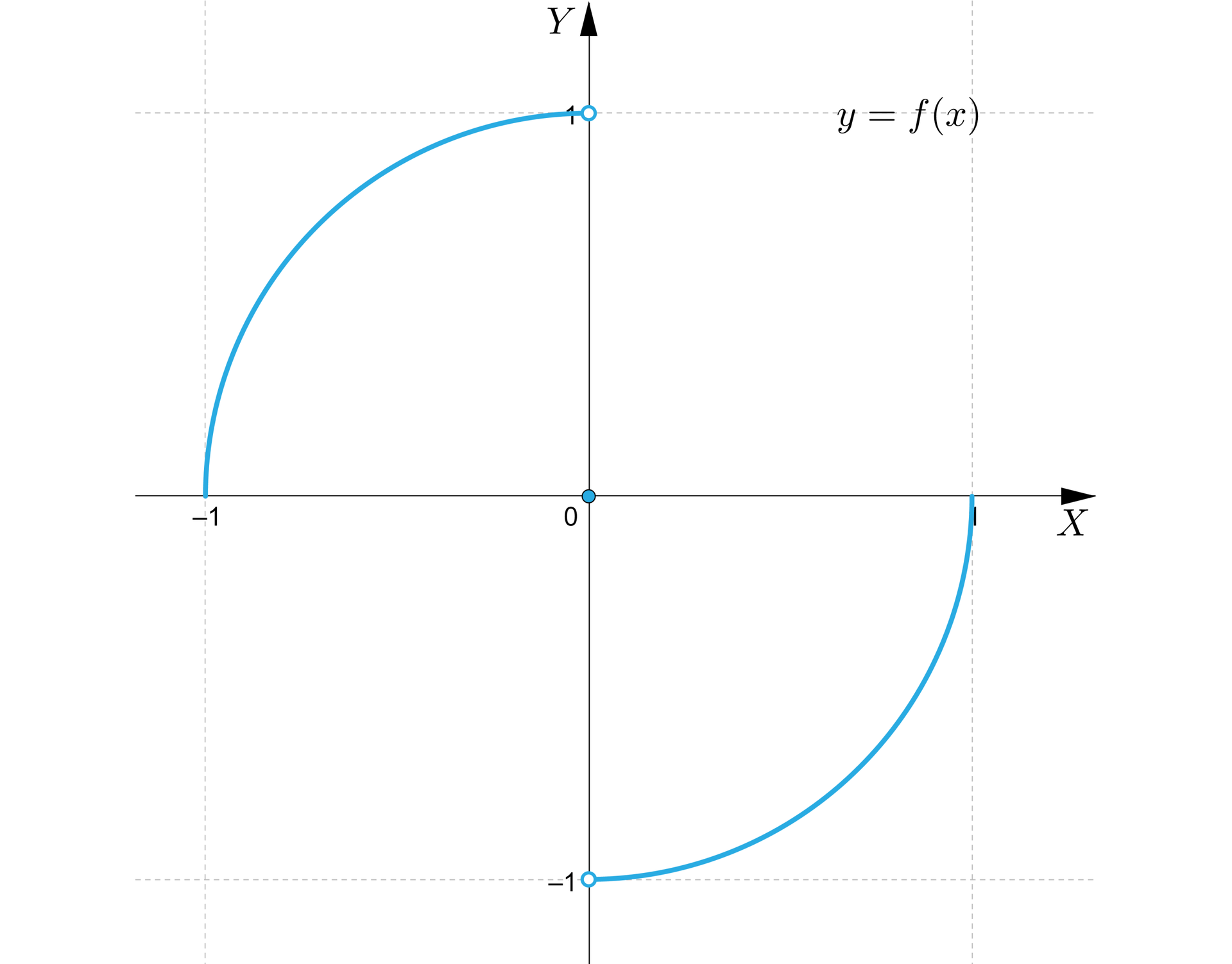
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do jeden oraz pionową osią Y od minus jeden do jeden. W układzie współrzędnych zaznaczono wykres funckji f , który składa się z dwóch krzywych oraz punktu. Pierwsza krzywa przypominająca kształtem ćwiartkę okręgu zaczyna się w zamalowanym punkcie -1,0 i łączy się z niezamalowanym punktem o współrzędnych 1,0. Druga krzywa przypominająca kształtem ćwiartkę koła zaczyna się w niezamalowanym punkcie -1,0 i łączy się z punktem o współrzędnych 1,0. Dodatkowo zaznaczony jest zamalowany punkt 0,0. — Wykres funkcji nieciągłej, nieosiągającej swoich kresów

Najważniejsze od tej pory jest to, że funkcje ciągłe określone na przedziale domkniętym na pewno osiągają swoje kresy. Dowiedzmy się teraz, jak tego użyć do znajdowania wartości ekstremalnych, czyli minimalnych i maksymalnych różnych funkcji.

Ekstrema funkcji ciągłych

Naszym podstawowym narzędziem szukania wartości ekstremalnych funkcji będzie warunek konieczny w postaci różniczkowej.

Warunek konieczny istnienia ekstremum. Jeżeli funkcja różniczkowalna $f$ ma w punkcie $x_{0}$ ekstremum lokalneekstremum lokalne funkcjiekstremum lokalne, to $x_{0}$ jest punktem stacjonarnympunkt stacjonarnypunktem stacjonarnym. Punkt stacjonarny to taki punkt $x_{0}$ w którym funkcja pochodna funkcji $f$ się zeruje, $f' (x_{0}) = 0$ , czyli w jakimś sensie „stoi w miejscu”, ani nie rośnie, ani nie maleje.

Podany powyżej warunek jest jedynie warunkiem koniecznym, ale nie jest to oczywiście warunek wystarczający, na przykład funkcja $y = x^{3} + 1$ ma punkt stacjonarny równy $x = 0$ , czyli jej wykres ma tam styczną poziomą, ale nie ma w tym punkcie ani minimum, ani maksimum.

R1JkChwKbGVF9

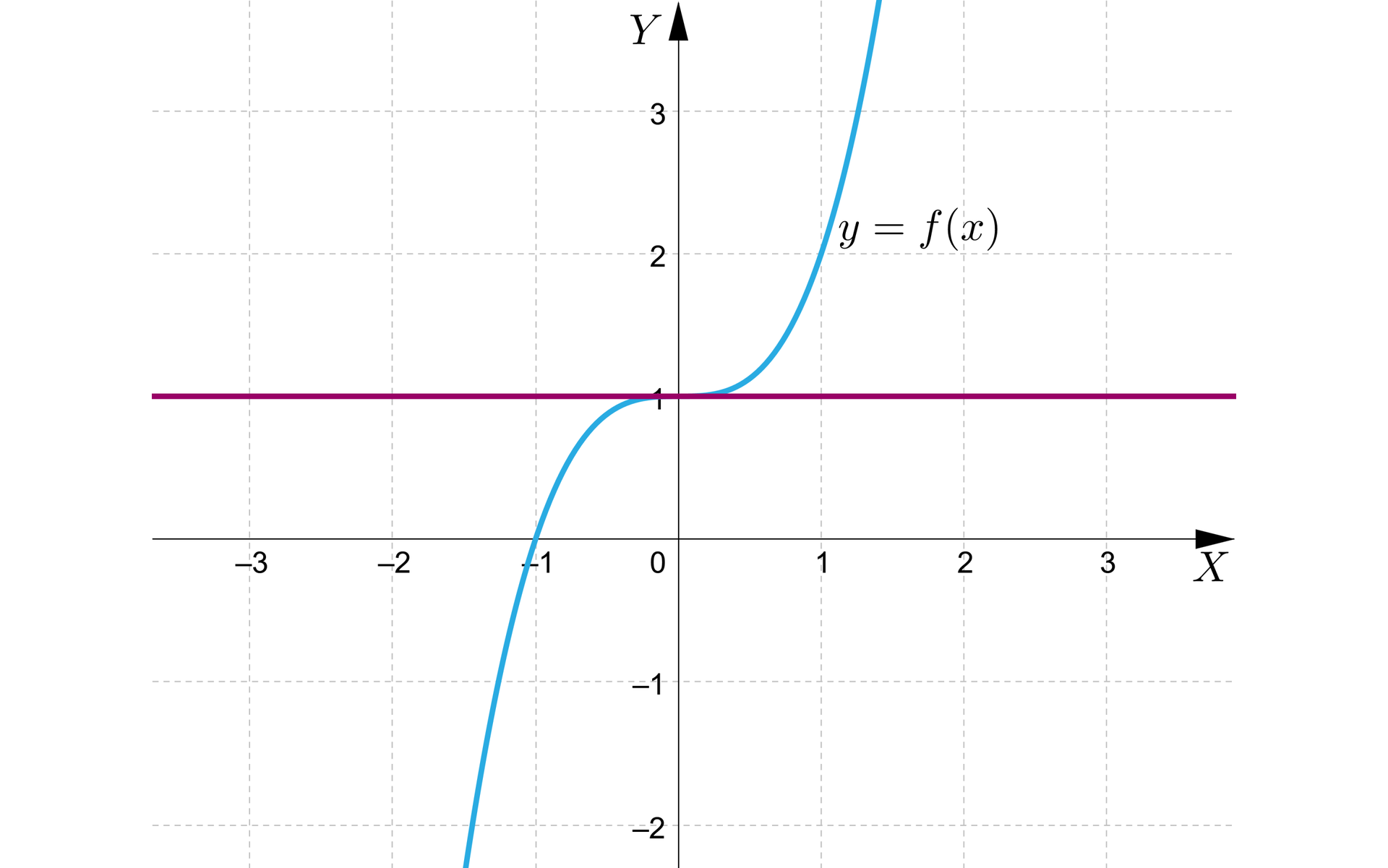
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus trzech do trzech oraz pionową osią Y od minus dwóch do trzech. W układzie współrzędnych zaznaczono wykres funckji f . Wykres biegnie od minus nieskończoności do punktu 1,0. W tym punkcie dochodzi do punktu przegięcia i następnie wykres dalej biegnie do nieskończoności. Zaznaczono również styczną poziomą do wykresu o równaniu y=1. — Wykres funkcji z punktem stacjonarnym bez ekstremum

W celu wyznaczenia ekstremów funkcji różniczkowalnej będziemy zatem postępować w taki sposób: najpierw znajdziemy wszystkie punkty stacjonarne funkcji, sprawdzimy wartości funkcji w tych punktach oraz na końcach dziedziny, porównany wszystkie wartości ze sobą, i w ten sposób znajdziemy wartość minimalną i maksymalną tej funkcji.

Przykład 1

Znajdziemy ekstrema funkcji $f (x) = x^{3} - 12 x$ określonej na przedziale $0 \leq x \leq 4$ .

Rozwiązanie

Jest to funkcja ciągła, więc na przedziale domkniętym przyjmuje na pewno swoje kresy, i różniczkowalna, czyli możemy szukać punktów stacjonarnych. Jej pochodna wynosi $f' (x) = 3 x^{2} - 12$ , przyrównanie pochodnej do zera daje równanie $3 x^{2} - 12 = 0$ , którego rozwiązaniami są $(- 2)$ i $2$ . Pierwszy z tych argumentów nie należy do naszej dziedziny, musimy go więc odrzucić.

Pozostaje nam sprawdzić wartości funkcji w trzech punktach – na obu brzegach dziedziny oraz w punkcie stacjonarnym. Mamy $f (0) = 0$ , $f (4) = 16$ i $f (2) = - 16$ , czyli wartością najmniejszą tej funkcji jest $(- 16)$ , a największą $16$ .

RVxY4EyEwDPeL

Ilustracja przedstawia układ współrzędnych z poziomą osią X od zera do czterech oraz pionową osią Y od minus dwudziestu do piętnastu. W układzie współrzędnych zaznaczono wykres funckji f . Wykres jest w postaci fragmentu paraboli z ramionami skierowanymi do góry, który zaczyna się w zamalowanym punkcie 0,0 łukiem pod osią X łączy się z punktem o współrzędnych 3,5;0 i dalej biegnie do zamalowanego punktu o współrzędnych 4,15.

Przykład 2

Znajdziemy ekstrema funkcji $f (x) = x^{3} + 12 x$ określonej na przedziale $0 \leq x \leq 4$ .

Rozwiązanie

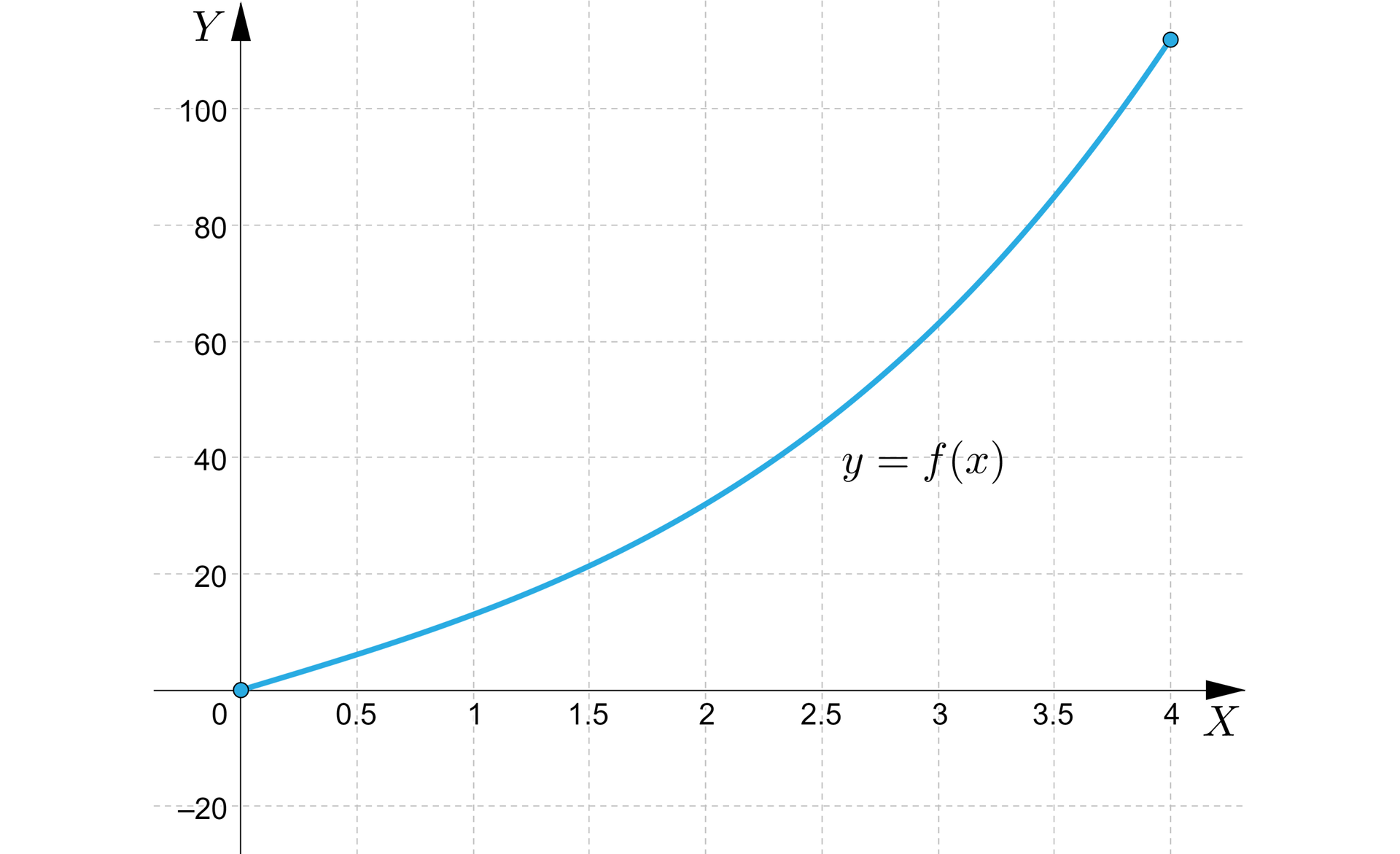
Jest to funkcja ciągła, więc na przedziale domkniętym przyjmuje na pewno swoje kresy, i różniczkowalna, czyli możemy szukać punktów stacjonarnych. Jej pochodna wynosi $f' (x) = 3 x^{2} + 12$ , przyrównanie pochodnej do zera daje równanie $3 x^{2} + 12 = 0$ , które nie posiada rozwiązań rzeczywistych. Musimy zatem sprawdzić jedynie wartości funkcji na obu brzegach dziedziny.

Mamy $f (0) = 0$ i $f (4) = 112$ , czyli wartością najmniejszą tej funkcji jest $0$ , a największą $112$ .

Zauważmy, że po wyznaczeniu pochodnej mogliśmy przeprowadzić inne rozumowanie – pochodna się nie zeruje, i jest cały czas dodatnia, co oznacza, że funkcja zawsze rośnie, czyli jej wartość na lewym krańcu dziedziny będzie jej wartością minimalną, a na prawym krańcu – maksymalną.

R1M4mEuYcs4Xe

Ilustracja przedstawia układ współrzędnych z poziomą osią X od zera do czterech oraz pionową osią Y od minus dwudziestu do stu. W układzie współrzędnych zaznaczono wykres funckji f . Wykres jest w postaci fragmentu paraboli z ramionami skierowanymi do góry, który zaczyna się w zamalowanym punkcie 0,0 łączy się z zamalowanym punktem o współrzędnych 4,112.

Przykład 3

Znajdziemy ekstrema funkcji $f (x) = x^{3} - \frac{9}{2} x^{2} - 12 x + 20$ określonej na przedziale $- 3 \leq x \leq 6$ .

Rozwiązanie

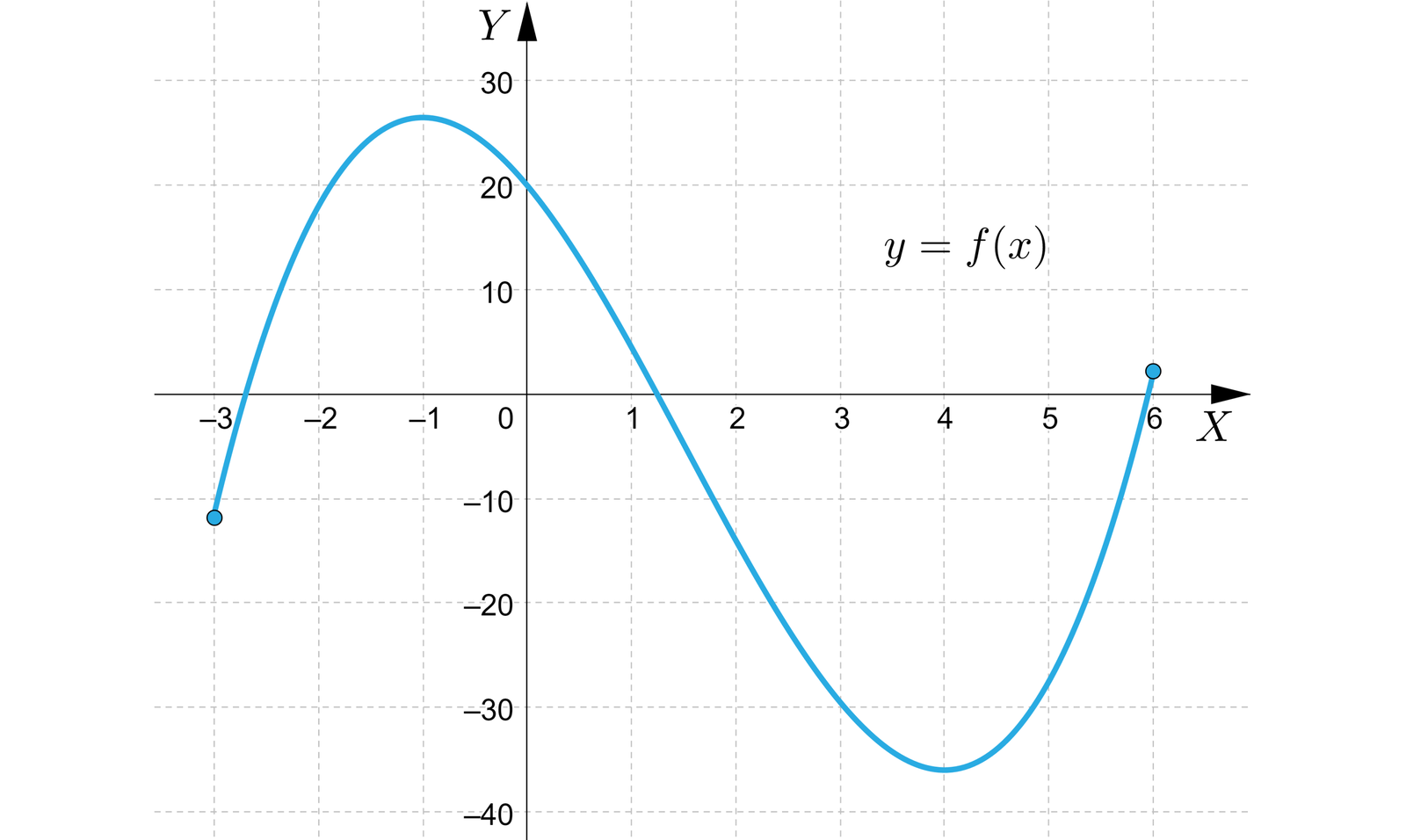
Ponownie jest to funkcja ciągła, więc na przedziale domkniętym przyjmuje na pewno swoje kresy, i różniczkowalna, czyli możemy szukać punktów stacjonarnych. Pochodna ma postać $f' (x) = 3 x^{2} - 9 x - 12$ , równanie na punkty stacjonarne ma postać $3 x^{2} - 9 x - 12 = 0$ , po uproszczeniu $x^{2} - 3 x - 4 = 0$ , którego rozwiązaniami są $(- 1)$ i $4$ . W celu wyznaczenia wartości ekstremalnych musimy w tym przypadku wyznaczyć i porównać wartości funkcji w czterech punktach – na obu brzegach dziedziny, oraz w dwóch punktach stacjonarnych.

Otrzymujemy $f (- 3) = - 11, 5$ , $f (6) = 2$ , $f (- 1) = 26, 5$ i $f (4) = - 36$ . Ostatecznie wartością najmniejszą funkcji jest $(- 36)$ , zaś największą $26, 5$ .

R1HSlE5KqFwmm

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus trzech do sześciu oraz pionową osią Y od minus czterdziestu do trzydziestu. W układzie współrzędnych zaznaczono wykres funckji f . Wykres zaczyna się w zamalowanym punkcie o współrzędnych -3;11,5 i biegnie do punktu -1;26,5. Następnie wykres biegnie do punktu 4,36 przebijając oś X i następnie biegnie do zamalowanego punktu 6,2.

Przykład 4

Znajdziemy ekstrema funkcji $f (x) = \sqrt[3]{x^{2}}$ określonej na przedziale $- 1 \leq x \leq 8$ .

Rozwiązanie

Ponownie jest to funkcja ciągła, więc na przedziale domkniętym przyjmuje na pewno swoje kresy, ale nie jest różniczkowalna w zerze, czyli nie wystarczy już znalezienie punktów stacjonarnych. Pochodna ma postać $f' (x) = \frac{2}{3 \sqrt[3]{x}}$ , $x \neq 0$ , i równanie na punkty stacjonarne nie ma rozwiązania. W celu wyznaczenia wartości ekstremalnych musimy w tym przypadku wyznaczyć i porównać wartości funkcji w trzech punktach – na obu brzegach dziedziny, oraz w punkcie nieróżniczkowalności.

Otrzymujemy $f (- 1) = 1$ , $f (8) = 4$ i $f (0) = 0$ . Ostatecznie wartością najmniejszą funkcji jest $0$ , zaś największą $4$ .

Rewx7w5Hqmys1

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus jeden do ośmiu oraz pionową osią Y od minus jeden do czterech. W układzie współrzędnych zaznaczono wykres funckji f . Wykres zaczyna się w zamalowanym punkcie o współrzędnych -1,1 i biegnie do początku układu współrzędnych i następnie biegnie do zamalowanego punktu 8,4.

Słownik

ekstremum lokalne funkcji

wartość najmniejsza lub największa, którą przyjmuje funkcja w pewnym otoczeniu

punkt stacjonarny

punkt, w którym styczna do wykresu funkcji jest pozioma

Wprowadzenie

Film samouczek

Twierdzenie Weierstrassa

Ekstrema funkcji ciągłych

Słownik