Wykres funkcji $y=-f\left(-x\right)$ otrzymujemy przez symetryczne odbicie wykresu funkcji $y=f\left(x\right)$ względem osi $X$ i względem osi $Y$.

W praktyce takie przekształcenie oznacza to, że wykres funkcji $f$ najpierw odbijamy symetrycznie względem osi $X$, a następnie tak otrzymany wykres odbijamy symetrycznie względem osi $Y$. Możemy też postąpić inaczej – najpierw wykres funkcji $f$ odbijamy symetrycznie względem osi $Y$, a następnie otrzymany wykres odbijamy symetrycznie względem osi $X$.

Wyznaczymy zbiór wartości funkcji funkcji $g\left(x\right)=-f\left(-x\right)$, jeżeli zbiorem wartości funkcji $f$ jest zbiór $\left\{-2,-1,0,1,3,5\right\}$. Dziedziną każdej z rozważanych funkcji jest zbiór liczb rzeczywistych.

Rozwiązanie:

Zbiorem wartości funkcji $g\left(x\right)=-f\left(-x\right)$ jest zbiór liczb:

$\left\{-5,-3,-1,0,1,2\right\}$.

W tabeli przedstawiono argumenty oraz odpowiadające im wartości funkcji $f$.

Wyznaczymy tabelę argumentów oraz odpowiadających im wartości funkcji określonej wzorem $g\left(x\right)=-f\left(-x\right)$.

Rozwiązanie:

Jeżeli $g\left(x\right)=-f\left(-x\right)$, to:

Na rysunku przedstawiono wykres funkcji $f$.

RjydFMr2VbT69

Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus pięciu do pięciu, oraz z pionową osią $Y$ od minus dwóch do pięciu. Na płaszczyźnie narysowano wykres funkcji $f\left(x\right)$. Wykres funkcji stanowi parabola z ramionami skierowanymi ku górze. Wierzchołek paraboli znajduje się w punkcie o współrzędnych $\left(2;-2\right)$. Funkcja przebiega przez punkty o współrzędnych $\left(0;2\right)$, oraz $\left(4;2\right)$.

Naszkicujemy wykres funkcji  $g$ określonej wzorem $g\left(x\right)=-f\left(-x\right)$, a następnie wyznaczymy:

a) zbiór wartości funkcji $g$,

b) przedziały monotoniczności funkcji $g$.

Rozwiązanie:

Wykres funkcji $g$ otrzymujemy, przekształcając wykres funkcji $f$ w symetrii względem początku układu współrzędnych.

Wobec tego:

Rb3OYPVlFriZo

Na ilustracji przedstawiono przekształcony wykres $g\left(x\right)$, który jest efektem przekształcenia wcześniejszej funkcji $f\left(x\right)$. Wykres funkcji $g\left(x\right)$ stanowi parabola z ramionami skierowanymi w dół. Wierzchołek paraboli znajduje się w punkcie o współrzędnych $\left(-2;2\right)$. Funkcja przebiega przez punkty o współrzędnych $\left(-4;-2\right)$, oraz $\left(0;-2\right)$.

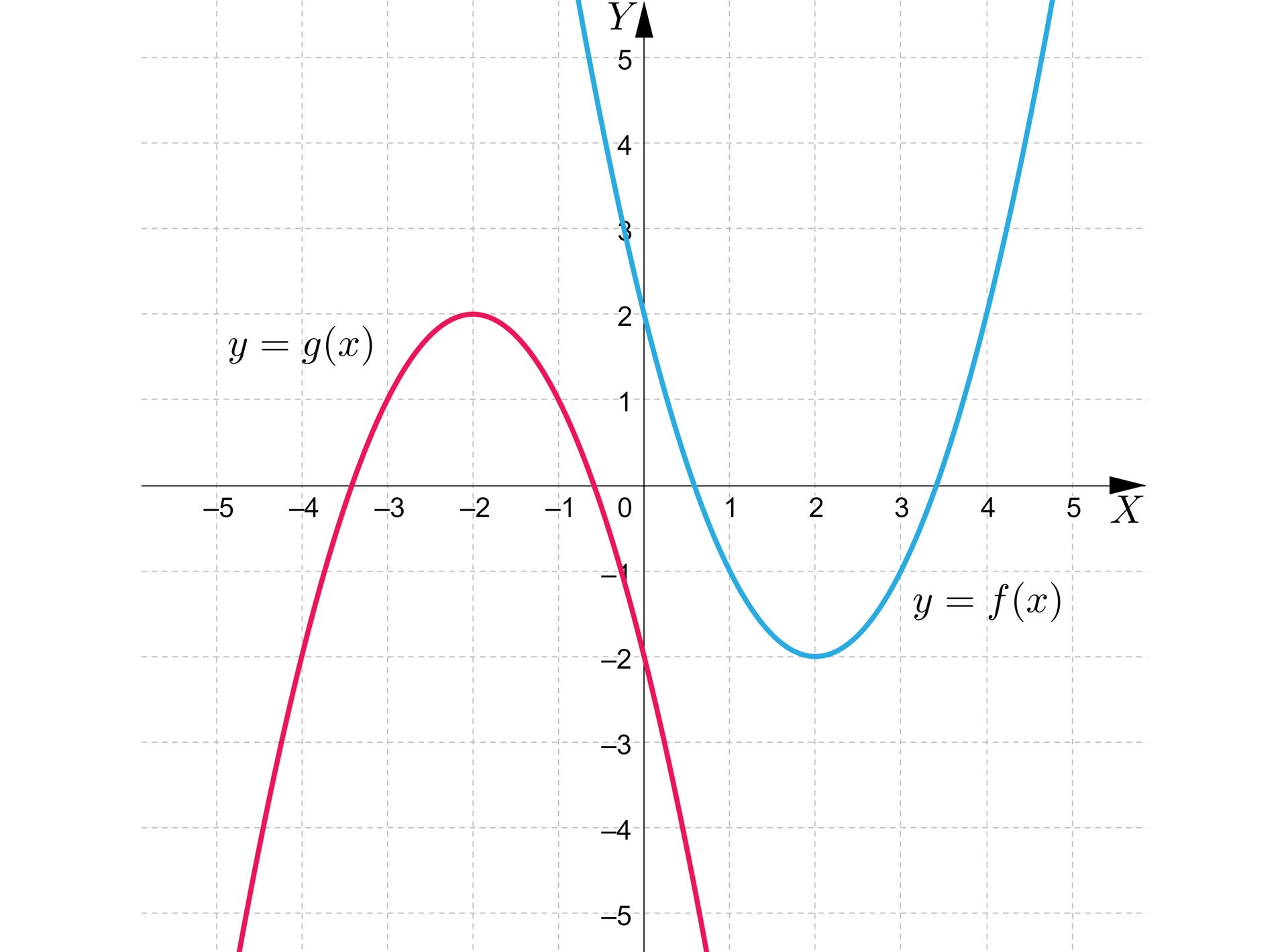
Z wykresu odczytujemy, że:

a) zbiorem wartości funkcji $g$ jest przedział $\left(-\infty ,2\right.⟩$,

b) funkcja $g$ jest:

• rosnąca w przedziale $\left(-\infty ,-2\right.⟩$,

• malejąca w przedziale $\left.⟨-2,\infty \right)$.

Rysunek przedstawia wykres funkcji $f$ określonej wzorem $f\left(x\right)=\sqrt{x-3}-1$.

Rcu66Be7qJ6DN

Ilustracja przedstawia układ współrzędnych z poziomą osią $X$ od minus dwóch do ośmiu, oraz z pionową osią $Y$ od minus dwóch do trzech. Na płaszczyźnie narysowano wykres funkcji $f\left(x\right)$, znajdującej się w pierwszej i czwartej ćwiartce układu współrzędnych. Wykres funkcji stanowi zakrzywiona linia o początku w punkcie o współrzędnych $\left(3;-1\right)$ i biegnie do plus nieskończoności przez punkt $\left(7;1\right)$.

Niech $g\left(x\right)=-f\left(-x\right)$.

Dla funkcji $g$:

a) wyznaczymy wzór funkcji,

b) naszkicujemy wykres,

c) określimy dziedzinę i zbiór wartości.

Rozwiązanie:

a) Ponieważ $g\left(x\right)=-f\left(-x\right)$, zatem

$g\left(x\right)=-f\left(-x\right)=-\sqrt{-x-3}+1$.

b) Wykres funkcji $g$ przedstawia się następująco:

R130VunY1rjQQ

Na ilustracji przedstawiono przekształcony wykres $g\left(x\right)$, który jest efektem przekształcenia wcześniejszej funkcji $f\left(x\right)$. Wykres funkcji $g\left(x\right)$ znajduje się w drugiej i trzeciej ćwiartce układu współrzędnych i stanowi go zakrzywiona linia zmierzająca od minus nieskończoności do punktu o współrzędnych $\left(-3;1\right)$. Przechodzi przez punkt $\left(7;-1\right)$.

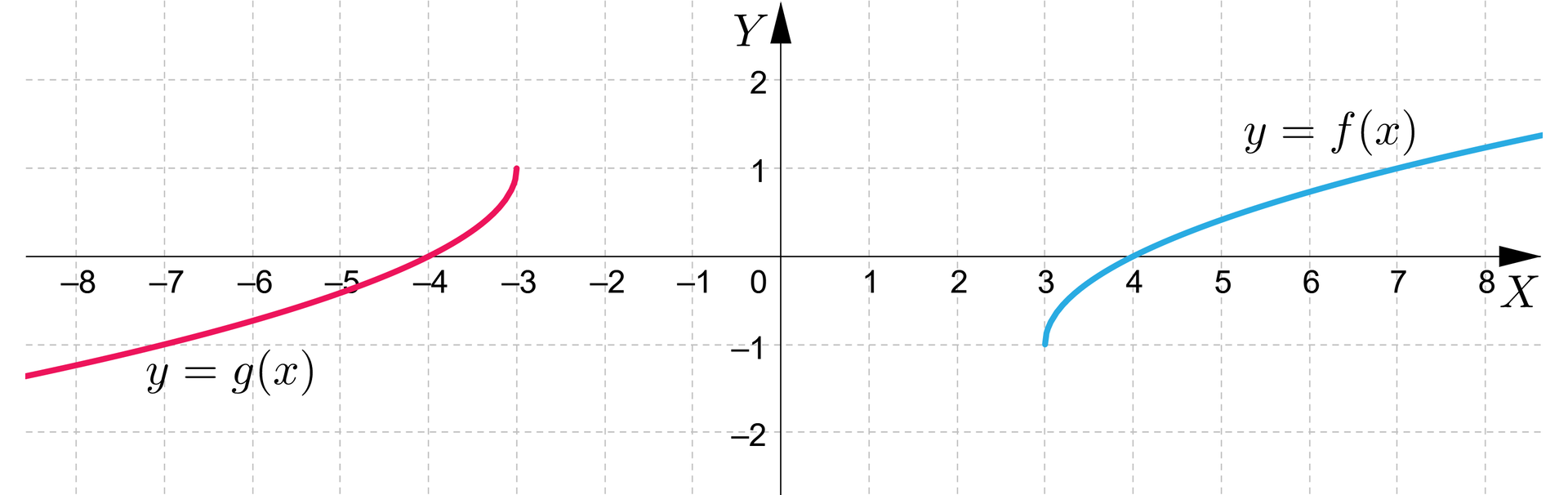
c) Dziedziną funkcji $g$ jest przedział $\left(-\infty ,-3\right.⟩$, a zbiorem wartości tej funkcji przedział $\left(-\infty ,1\right.⟩$.

Wyznaczymy wzór funkcji $g\left(x\right)=-f\left(-x\right)$, jeżeli funkcja $f$ jest określona wzorem:

a) $f\left(x\right)=x^2-x+1$,

b) $f\left(x\right)=\frac{x+1}{3-x}$.

Rozwiązanie:

Jeżeli $g\left(x\right)=-f\left(-x\right)$, to:

a) $g\left(x\right)=-f\left(-x\right)=-\left({\left(-x\right)}^2-\left(-x\right)+1\right)=-\left(x^2+x+1\right)=-x^2-x-1$,

b) $g\left(x\right)=-f\left(-x\right)=-\frac{-x+1}{3-\left(-x\right)}=\frac{x-1}{3+x}$.

Zauważmy, że $D_f=\mathrm{ℝ}\setminus \left\{3\right\}$ oraz $D_g=\mathrm{ℝ}\setminus \left\{-3\right\}$.

Wykażemy, że jeśli funkcja $f$ wyraża się wzorem $f\left(x\right)=ax$, gdzie $a, x\in \mathrm{ℝ}$, to funkcja $f$ i funkcja $g$ określona wzorem $g\left(x\right)=-f\left(-x\right)$ są równe.

Rozwiązanie:

Mówimy, że funkcje $f$ i $g$ są równe, wtedy i tylko wtedy, gdy mają te same dziedziny oraz dla każdego $x\in D_f=D_g$ zachodzi warunek $f\left(x\right)=g\left(x\right)$.

Niech $x\in D_f=D_g$. Wówczas:

$g\left(x\right)=-f\left(-x\right)=-a·\left(-x\right)=a·x=ax=f\left(x\right)$

Wobec tego funkcje $f$ i $g$ są równe.

• symetryczne odbicie wykresu funkcji przez symetrię względem osi $X$ i osi $Y$,

• symetryczne odbicie wykresu funkcji względem początku układu współrzędnych

zbiór punktów płaszczyzny o współrzędnych $\left(x,y\right)$, które spełniają zależność $y=f\left(x\right)$