Przeczytaj

Przypomnijmy, że odcinki dwóch stycznych poprowadzonych do danego okręgu z punktu $P$ leżącego zewnątrz okręgu, wyznaczone przez punkt $P$ i punkty styczności, są sobie równe. Oto zasadnicze twierdzenie planimetriizasadnicze twierdzenie planimetriizasadnicze twierdzenie planimetrii:

Rov9H8XmucwWN

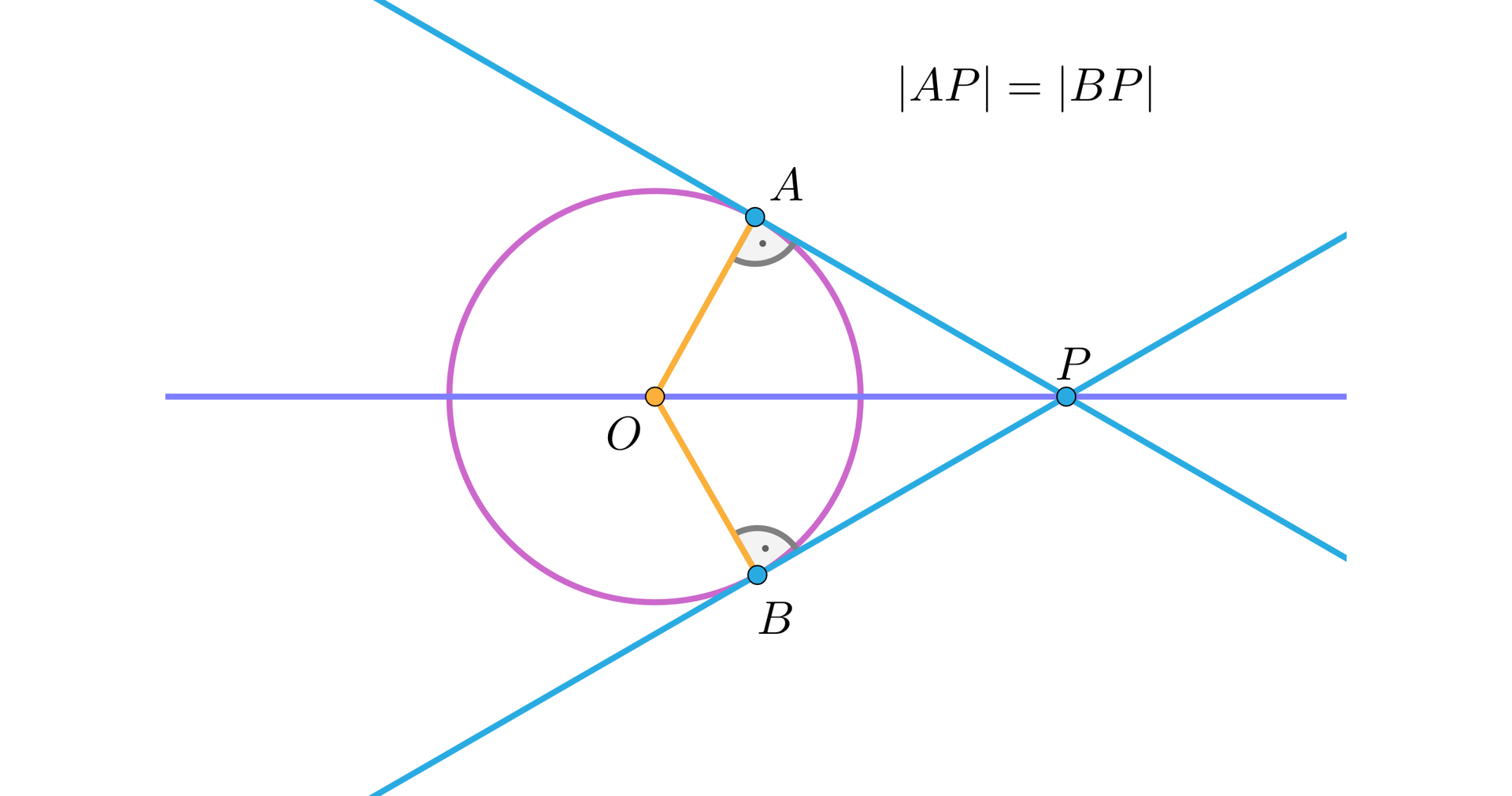
Ilustracja przedstawia okrąg o środku O. Poprowadzono do niego dwie styczne o odcinkach AP i BP które są równe. Odcinki AO i BO są promieniami okręgu.

Powyższy fakt wykorzystamy dla dowodu poniższych dwóch twierdzeń, które podają warunki koniczne i wystarczające, by w dany czworokąt można było wpisać okrąg.

warunek konieczny, by czworokąt można było opisać na okręgu

Twierdzenie: warunek konieczny, by czworokąt można było opisać na okręgu

Jeśli czworokąt jest opisany na okręgu, to sumy długości przeciwległych boków tego czworokąta są sobie równe.

Dowód

Rozważmy czworokąt $A B C D$ opisany na okręgu. Niech punkty $P$ , $Q$ , $R$ , $S$ będą odpowiednimi punktami styczności okręgu i boków danego wielokąta, jak na rysunku.

RoBV7WQNpRNeU

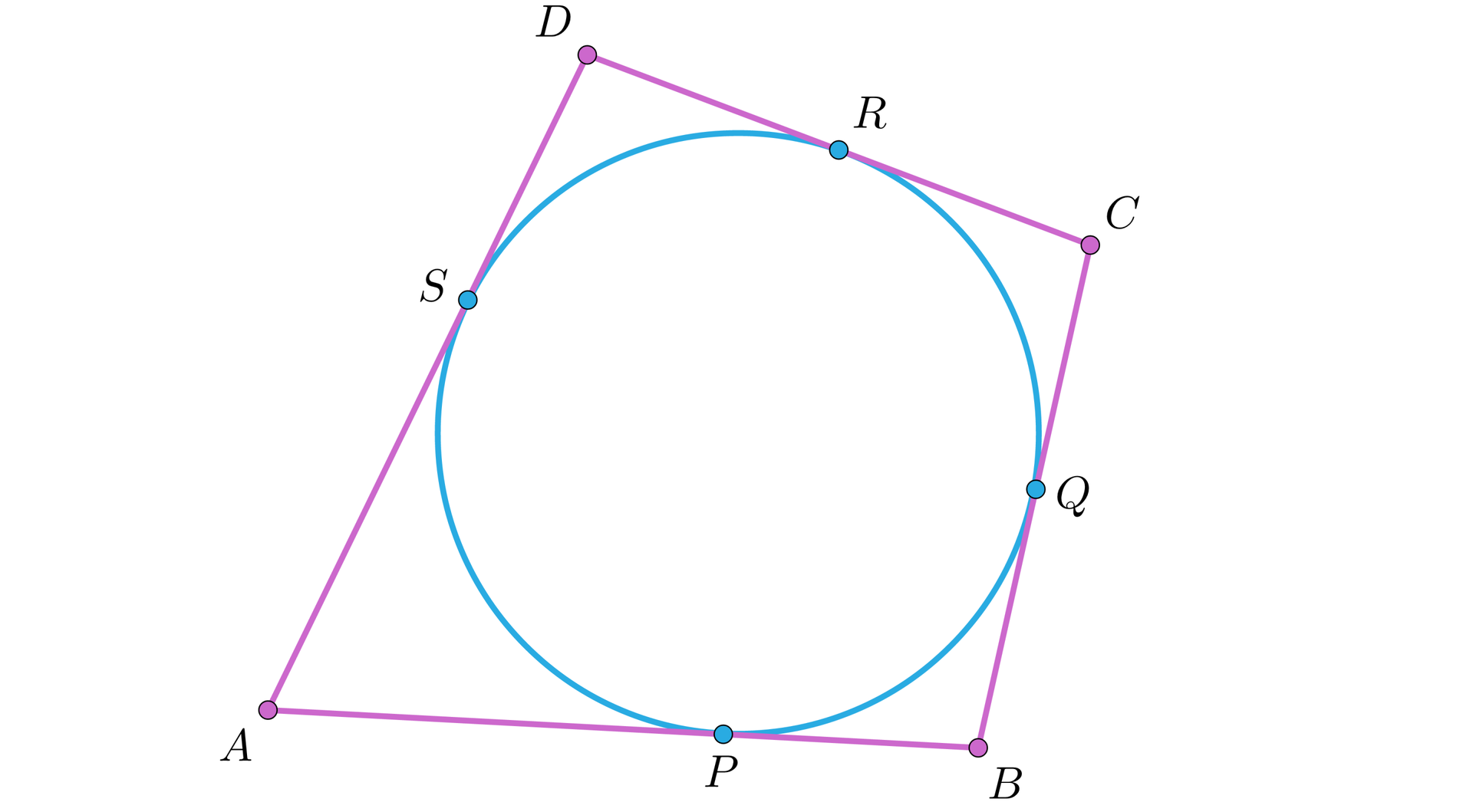
Ilustracja przedstawia czworokąt ABCD opisany na okręgu. Punkty P, Q, R, S są punktami styczności okręgu i boków czworokąta.

Wtedy z twierdzenia o odcinkach stycznych mamy: $|A P| = |A S|$ , $|B P| = |B Q|$ , $|C Q| = |C R|$ , $|D R| = |D S|$ .

Ponieważ: $|A B| = |A P| + |B P|$ , $|B C| = |B Q| + |C Q|$ , $|C D| = |C R| + |D R|$ oraz $|A D| = |A S| + |D S|$ , więc

$|A B| + |C D| = (|A P| + |B P|) + (|C R| + |D R|) =$

$= (|A S| + |B Q|) + (|C Q| + |D S|) =$

$= (|B Q| + |C Q|) + (|A S| + |D S|) = |B C| + |A D|$

Co należało udowodnić.

warunek wystarczający, by czworokąt można było opisać na okręgu

Twierdzenie: warunek wystarczający, by czworokąt można było opisać na okręgu

Jeżeli w czworokącie wypukłym sumy długości boków przeciwległych są sobie równe, to istnieje okrąg wpisany w ten czworokąt.

Dowód

Rozważmy czworokąt $A B C D$ spełniający warunek $|A B| + |C D| = |B C| + |A D|$ i rozważmy okrąg styczny do boków $A B$ , $A D$ i $C D$ – okrąg taki oczywiście istnieje, a jego środek jest jednoznacznie wyznaczony przez punkt przecięcia się dwusiecznych kątów $B A D$ i $A D C$ . Odpowiednie punkty styczności oznaczymy przez $P$ , $R$ , $S$ .

Przypuśćmy, że bok $B C$ nie jest styczny do tego okręgu. Wtedy można byłoby z punktu $B$ poprowadzić styczną do danego okręgu, która wyznaczyłaby na prostej $C D$ punkt $E$ różny od punktu $C$ (zapoznaj się z rysunkiem).

RbdxBsFpFGAc9

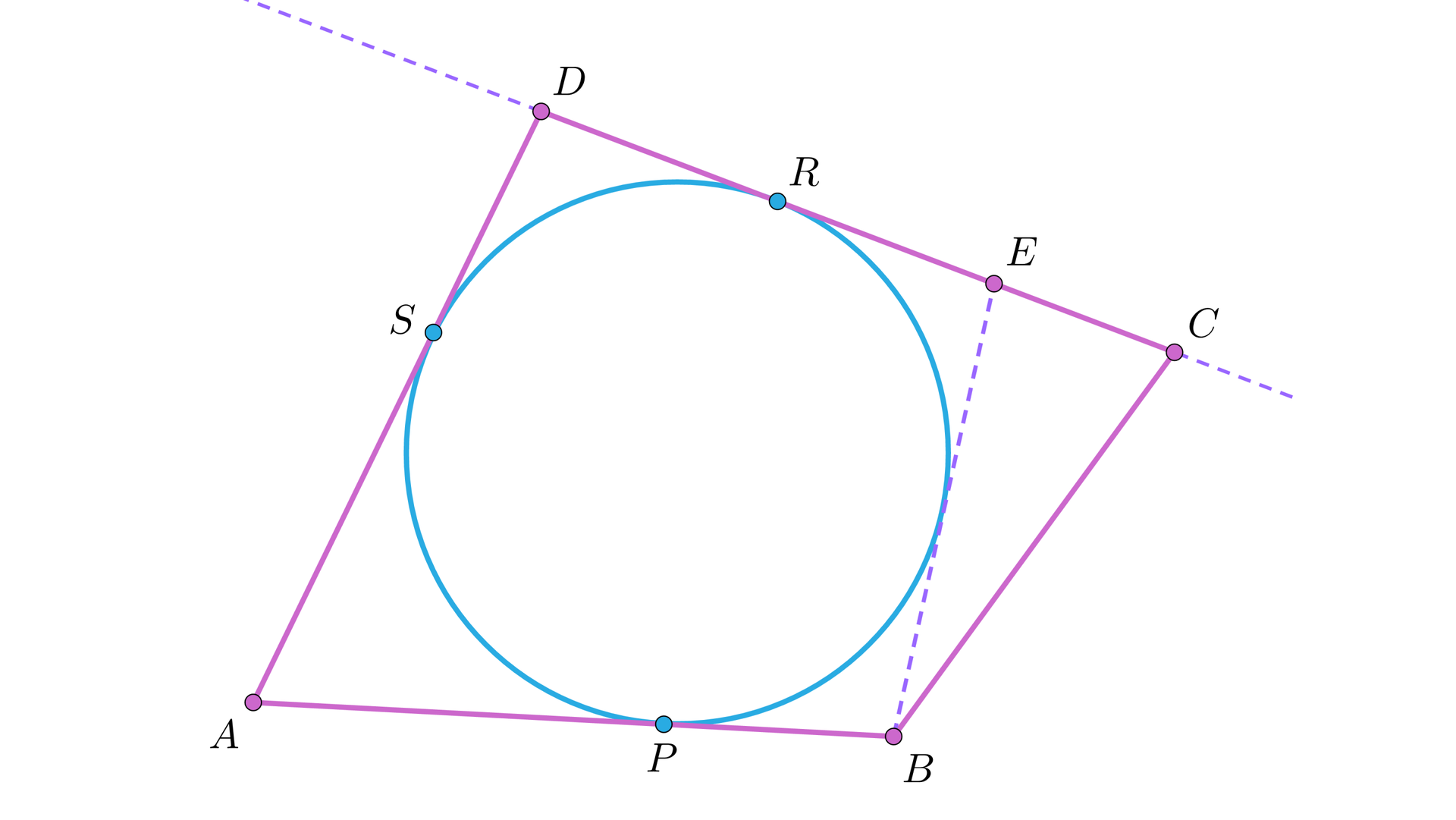
Ilustracja przedstawia czworokąt ABCD opisany na okręgu. Punkty P, R, S są punktami styczności okręgu i boków czworokąta. Bok BC nie jest styczny do okręgu. Dorysowano bok BE styczny do okręgu.

Jak widać na rysunku, dowód przeprowadzimy w przypadku, gdy punkt $E$ leży między punktami $D$ i $C$ (w przypadku, gdyby punkt $C$ leżał między punktami $D$ i $E$ , dowód przebiegałby analogicznie). Z warunku koniecznego dla czworokąta $A B E D$ opisanego na okręgu mielibyśmy, że $|A B| + |E D| = |B E| + |A D|$ .

Ostatnia równość wraz założeniem pozwalają zapisać układ równań:

$\{\begin{cases} |A B| + |C D| = |B C| + |A D| \\ |A B| + |E D| = |B E| + |A D| \end{cases}$

Odejmując stronami równania układu mamy: $|C D| - |E D| = |B C| - |B E|$ , czyli $|E C| = |B C| - |B E|$ . Stąd $|E C| + |B E| = |B C|$ .

Otrzymaliśmy równość sprzeczną z nierównością trójkąta, dla trójkąta $B C E$ , co dowodzi, że nasze przypuszczenie, iż bok $B C$ nie jest styczny do okręgu jest fałszywe. Otrzymana sprzeczność kończy dowód.

Przykład 1

Rozważmy czworokąt $A B C D$ opisany na okręgu o średnicy $4$ , w którym $|A B| = 4$ , $|B C| = 3$ , $|C D| = 5$ , jak na rysunku.

RpOBdo2alflAm

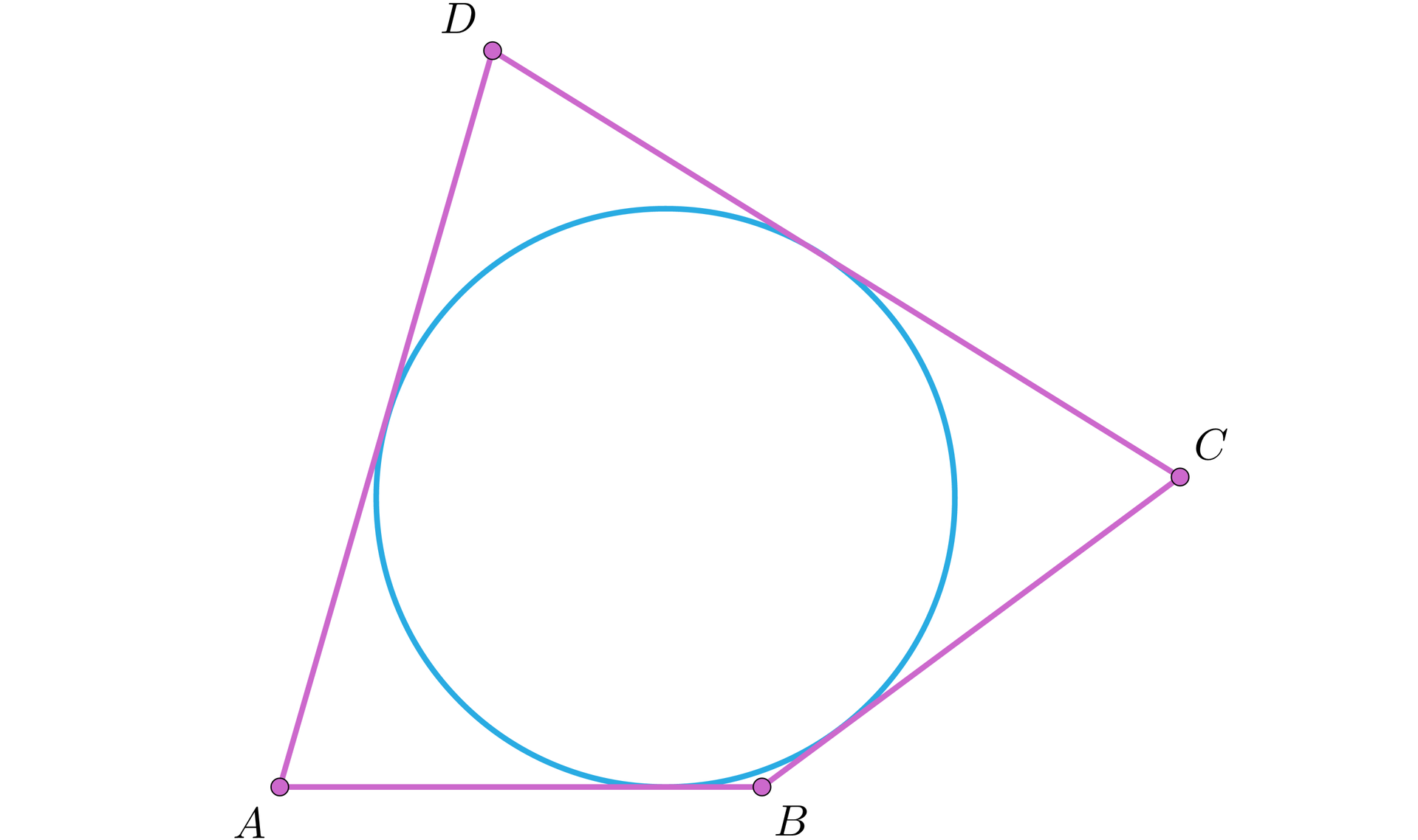
Ilustracja przedstawia czworokąt ABCD opisany na okręgu.

Obliczymy stosunek pola danego czworokąta do pola koła wpisanego w ten czworokąt.

Oczywiście pole $P_{K}$ koła jest równe $P_{K} = 4 π$ .

Z twierdzenia o czworokącie wpisanym w okrąg wynika, że $|A B| + |C D| = |B C| + |A D|$ , czyli $4 + 5 = 3 + |A D|$ . Stąd $|A D| = 6$ .

Zauważmy, że prowadząc odcinki ze środka okręgu do wierzchołków czworokąta dokonamy jego podziału na trójkąty, których podstawy są bokami czworokąta, a wysokościami poprowadzonymi na te podstawy są promienie okręgu (koła) wpisanego, jak na rysunku.

R1EDHNOAAMUJH

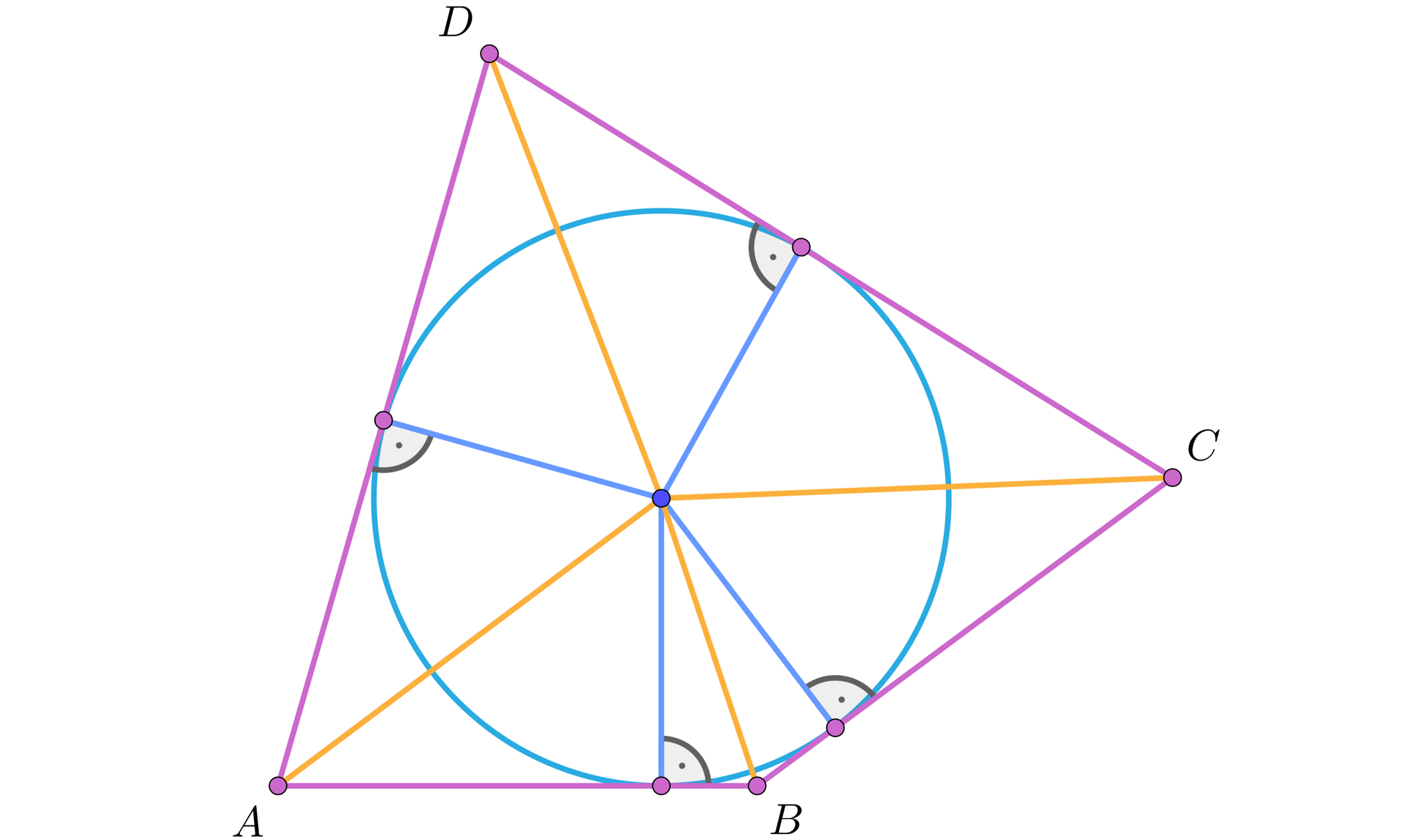
Ilustracja przedstawia czworokąt ABCD opisany na okręgu. Poprowadzono odcinki z wierzchołków czworokąta do środka okręgu. Zaznaczono promienie okręgu prostopadle do boków czworokąta.

Zatem pole czworokąta $P_{A B C D}$ można wyrazić, jako sumę pól odpowiednich trójkątów, czyli $P_{A B C D} = \frac{1}{2} |A B| \cdot r + \frac{1}{2} |B C| \cdot r + \frac{1}{2} |C D| \cdot r + \frac{1}{2} |A D| \cdot r =$

$= \frac{(|A B| + |B C| + |C D| + |A D|) \cdot r}{2}$ .

Stąd $P_{A B C D} = \frac{(3 + 4 + 5 + 6) \cdot 2}{2} = 18$ , a stosunek pól jest równy $\frac{P_{A B C D}}{P_{K}} = \frac{18}{4 π} = \frac{9}{2 π}$ .

W przykładzie wykazaliśmy, że pole czworokąta opisanego na okręgu jest równe połowie obwodu tego czworokąta przez długość promienia okręgu wpisanego. Pozostaje zauważyć, że ta własność dotyczy każdego wielokąta wypukłego, w który można wpisać okrąg.

Przykład 2

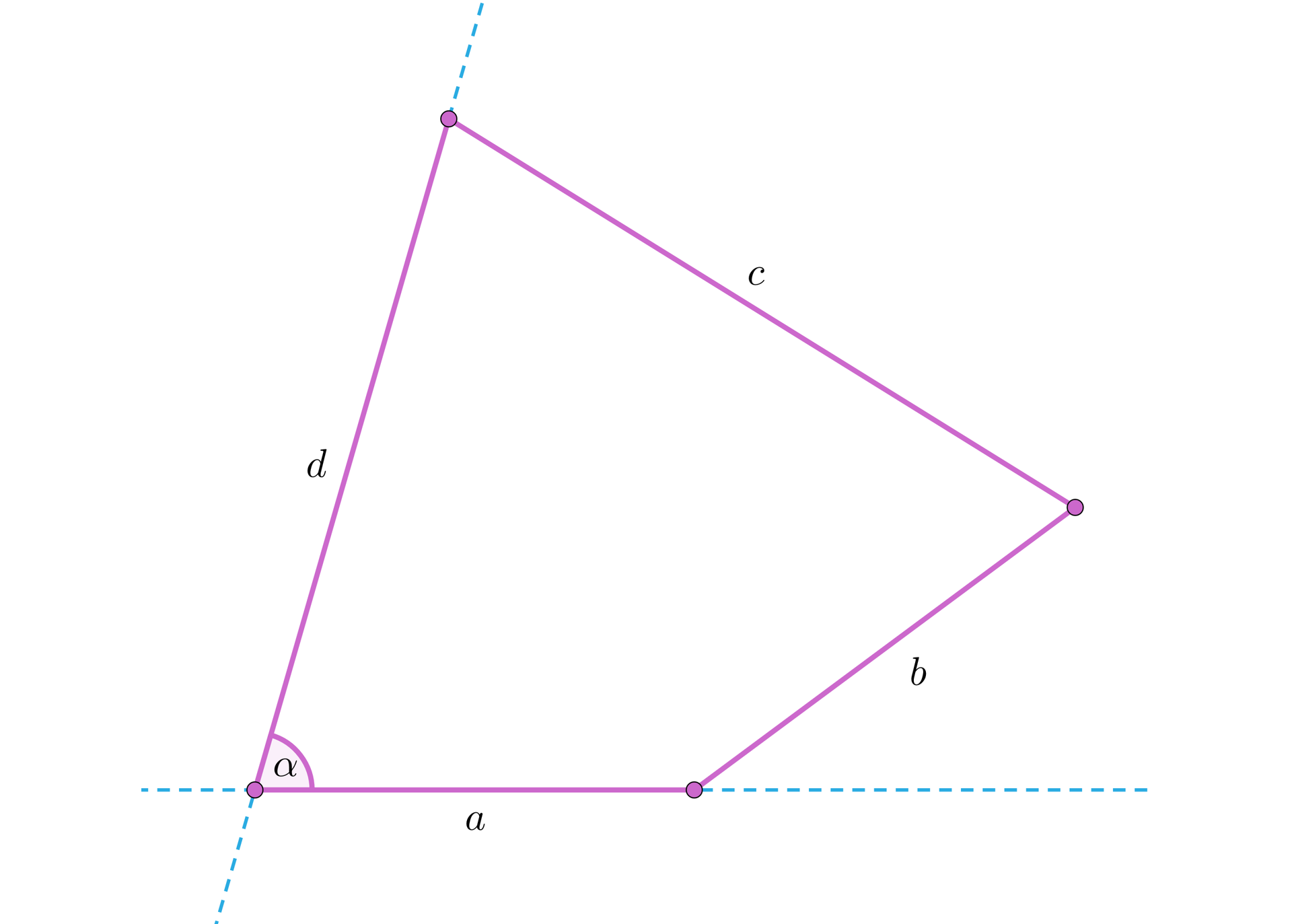
Przejdźmy teraz do klasycznej geometrii, czyli geometrii cyrkla i linijki. Zajmiemy się konstrukcją czworokąta, który da się opisać na okręgu. Przyjmijmy, że mamy dane odcinki $a$ , $b$ , $c$ równe kolejnym bokom czworokąta oraz kąt $α$ równy kątowi między bokiem $a$ i czwartym, nieznanym bokiem czworokąta.

Etapy konstrukcji.

Na prostej odkładamy sumę odcinków $a + c$ , a następnie od jednego z końców odejmujemy odcinek $b$ . W wyniku otrzymamy odcinek $d$ równy długości czwartego boku czworokąta.
Na prostej odkładamy odcinek $a$ , a następnie odkładamy kąt $α$ w taki sposób, by jedno z ramion zawierała odcinek $a$ a wierzchołkiem kąta był jeden z końców tego odcinka.
Z wierzchołka kąta, na drugim ramieniu odkładamy odcinek $d$ - w wyniku otrzymujemy trzy wierzchołki konstruowanego czworokąta.
Dla dokończenia konstrukcji pozostaje z tych wierzchołków, które nie są wierzchołkiem kąta $α$ wykreślić łuki odpowiednio równe $b$ i $c$ , aż do ich przecięcia.

Zauważmy, że warunkiem wykonalności konstrukcji jest, by suma $b + c$ była dłuższa od odległości wierzchołków leżących na ramionach kąta $α$ .

R2KHloAf5LoPN

Ilustracja przedstawia czworokąt o bokach a,b,c i d. Kąt pomiędzy bokami a i d wynosi alfa.

Słownik

zasadnicze twierdzenie planimetrii

twierdzenie, które orzeka, że odcinki dwóch stycznych poprowadzonych do danego okręgu z punktu $P$ leżącego zewnątrz okręgu, wyznaczone przez punkt $P$ i punkty styczności, są sobie równe

Wprowadzenie

Aplet

Słownik