Przeczytaj
Wyobraźmy sobie walec wpisany w stożek. Zastanówmy się: jakie warunki muszą być spełnione, aby walec wpisać w stożek? W jaki sposób wykreślić walec wpisany w stożek na kartce papieru? W odpowiedzi na te pytania pomoże nam aplet Geogebry.
Zapoznaj się z jego opisem i spróbuj odpowiedzieć na powyższe pytania.
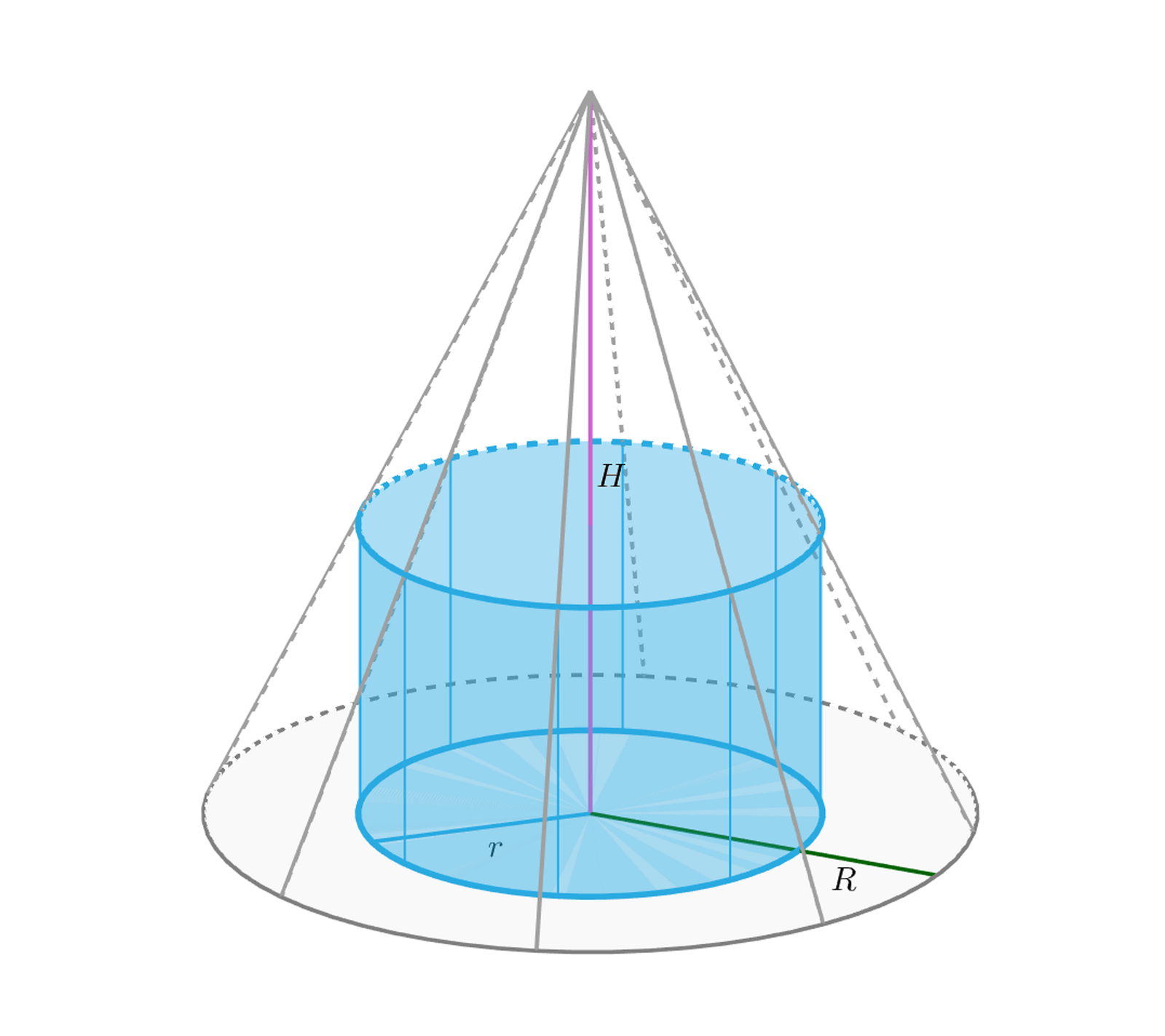
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DKUB8AZSR
Walec jest wpisany w stożek wtedy i tylko wtedy, gdy jedna z podstaw walca jest zawarta w podstawie stożka a brzeg drugiej podstawy walca zawiera się w powierzchni bocznej stożka.
Zadania dotyczące walca wpisanego w stożek można sprowadzić do prostych zadań geometrii płaskiej.
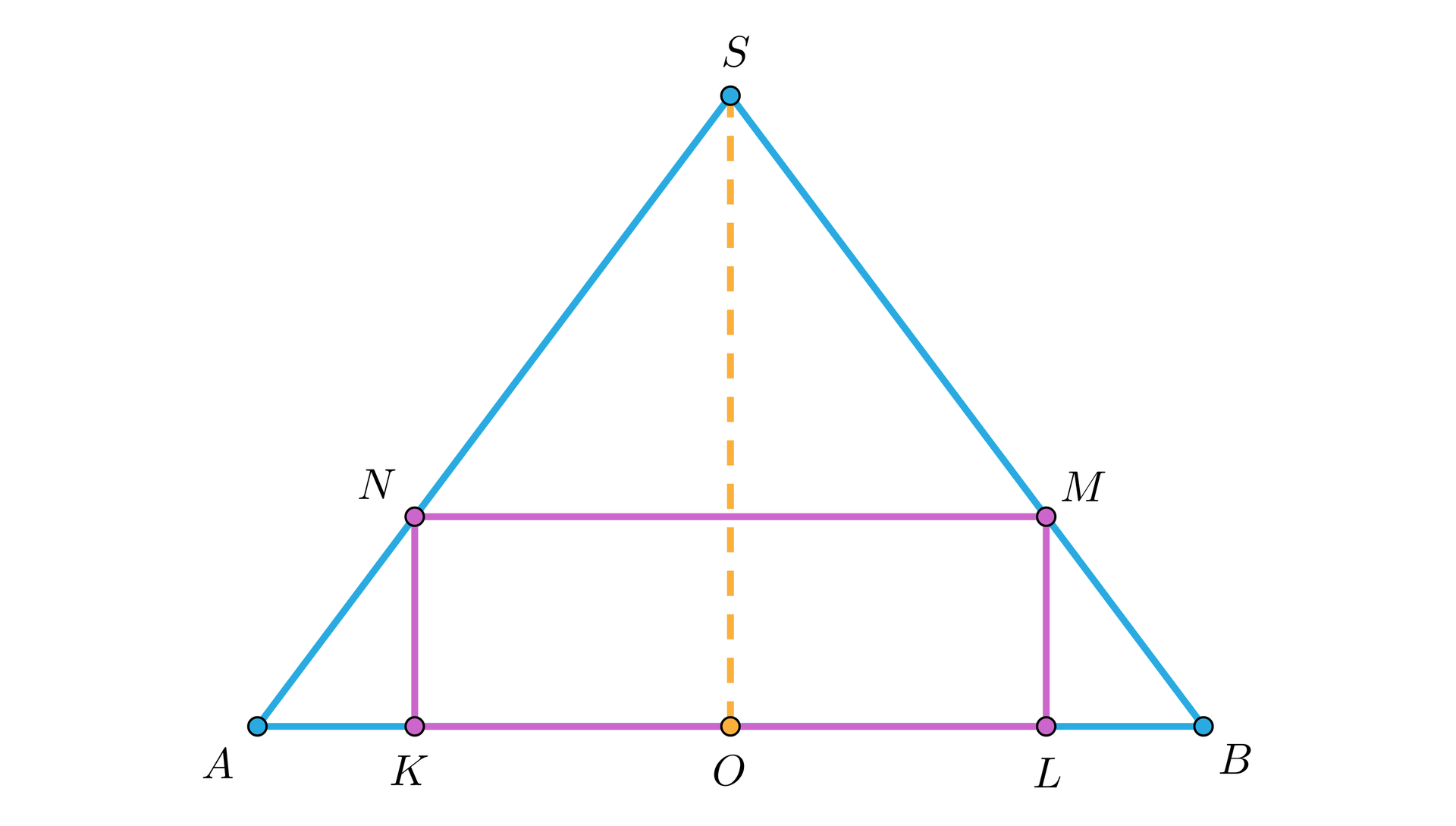
Na rysunku poniżej przedstawiono przekrój osiowy walca wpisanego w stożek. Przekrój osiowy tych brył jest prostokątem wpisanym w trójkąt równoramienny. Spostrzeżenie to pomoże nam w uproszczeniu planowania strategii rozwiązania wielu zadań geometrii przestrzennej.
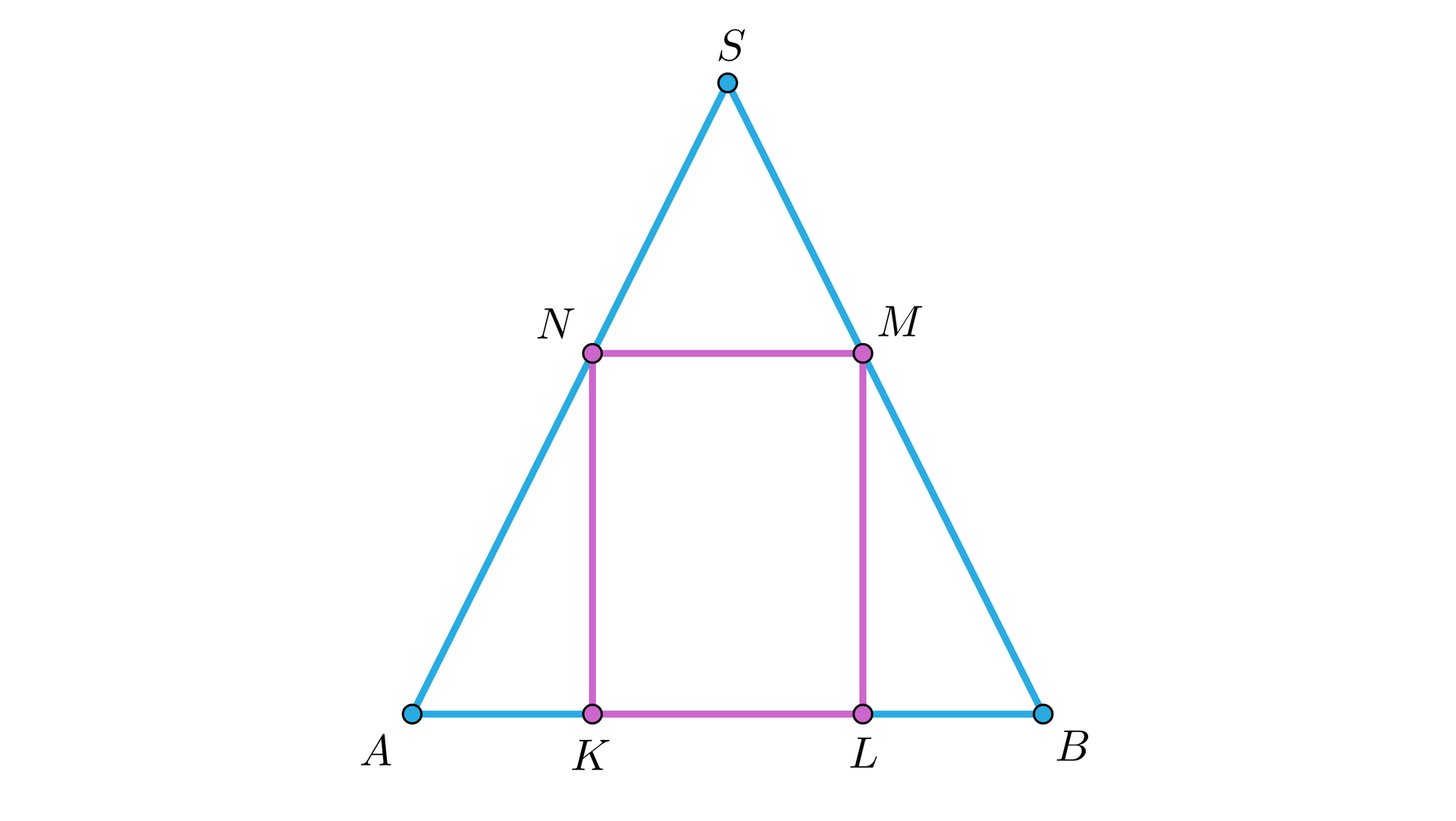
Poprowadźmy wysokość stożka .

Zauważmy, że trójkąty , , są trójkątami podobnym na podstawie cechy kąt, kąt, kąt. Fakt ten będzie pomocny w planowaniu strategii rozwiązywania zadań dotyczących walca wpisanego w stożek.
Pierwsze trzy przykłady pokazują, w jaki sposób można wykorzystać podobieństwo odpowiednich trójkątów w tego typu zadaniach.
Walec o wysokości, której długość wynosi wpisano w stożek. Przekrojem osiowym stożkaPrzekrojem osiowym stożka jest trójkąt równoboczny o boku długości . Obliczmy długość promienia podstawy walca wpisanego w ten stożek.
Rozwiązanie:
Wykreślmy przekrój osiowy brył opisanych w zadaniu.
Przyjmijmy oznaczenia, które pozwolą prowadzić rozwiązanie postawionego problemu.
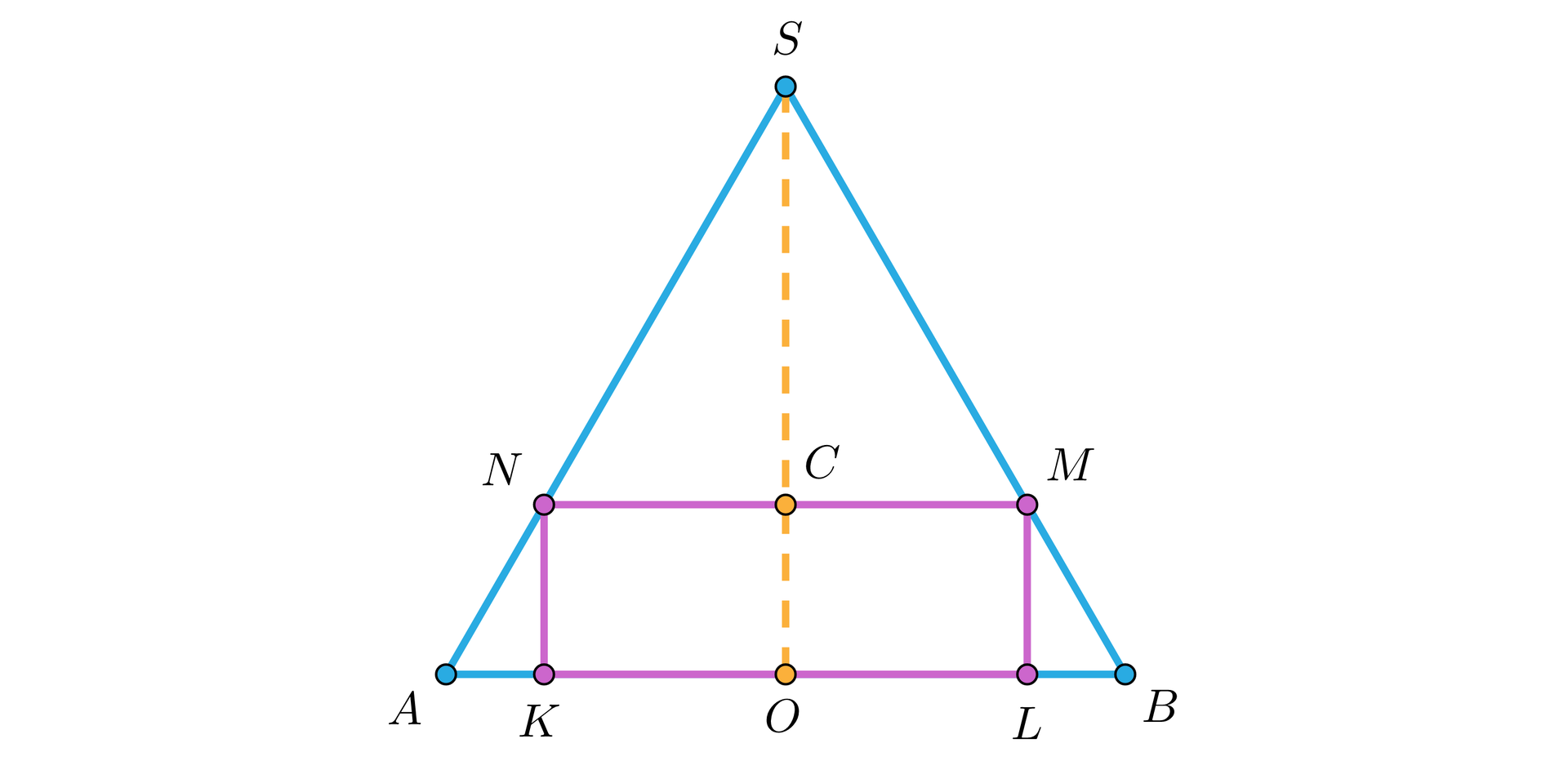
– długość promienia podstawy walca;
– długość wysokości walca;
– długość promienia podstawy stożka;
– długość wysokości stożka.
Z warunków zadania wiemy, że , i jako długość wysokości trójkąta równobocznego.
Zauważmy, że trójkąt jest podobny do trójkąta na podstawie cechy kąt, kąt, kąt.
Wynika stąd zależność , zatem , stąd , stąd ostatecznie mamy .
Walec, którego przekrojem osiowym jest kwadrat, wpisano w stożek o wysokości długości i promieniu podstawy długości . Obliczmy długość promienia podstawy walca.
Rozwiązanie:
Wykonujemy czytelny rysunek i przyjmujemy oznaczenia. Wystarczy narysować przekrój osiowy walcaprzekrój osiowy walca wpisanego w stożek.

– długość promienia podstawy walca;
– długość wysokości walca;
– długość promienia podstawy stożka;
– długość wysokości stożka.
Z warunków zadania mamy: oraz . Ponieważ przekrój walca jest kwadratem, to .
Zauważmy, że trójkąt jest podobny do trójkąta , stąd mamy zależność , zatem . Stąd wynika, że . Ostatecznie otrzymujemy .
W stożek o promieniu podstawy długości wpisano walec o wysokości długości i promieniu podstawy długości . Wyznaczmy długość wysokości stożka.
Rozwiązanie:
Wykonujemy rysunek przedstawiający tę sytuację.

Przyjmujemy oznaczenia.
– długość promienia podstawy walca;
– długość wysokości walca;
– długość promienia podstawy stożka;
– długość wysokości stożka.
Zauważmy, że trójkąt jest podobny do trójkąta , stąd mamy zależność .
Z warunków zadania otrzymujemy zatem , stąd .
W stożek wpisano walec. Długość wysokości walca jest równa długości promienia podstawy stożka.
Wyznacz tangens kąta zawartego pomiędzy wysokością stożka a jego tworzącą, wiedząc, że stosunek pola powierzchni całkowitej walca do pola powierzchni podstawy stożka wynosi .
Rozwiązanie:
Rozwiązanie zadania zaczynamy od wykonania czytelnego rysunku i przyjęcia oznaczeń. Wystarczy naszkicować odpowiedni przekrój osiowy.
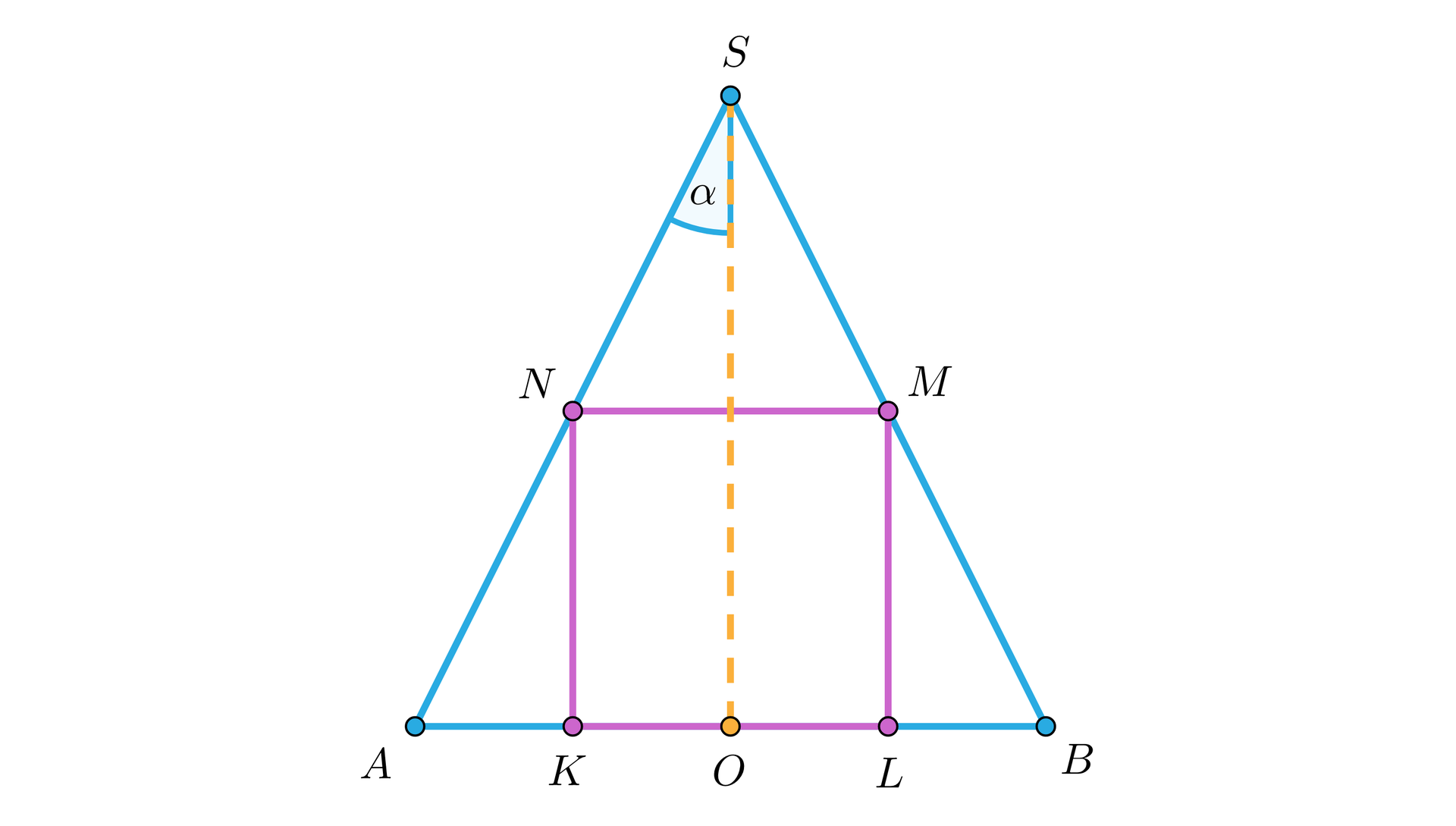
– długość promienia podstawy walca;
– długość wysokości walca;
– długość promienia podstawy stożka;
– długość wysokości stożka.
Z warunków zadania mamy i . Stąd po podstawieniu otrzymujemy zależność , zatem .
Zauważmy, że , zatem z trójkąta mamy , stąd .
Otrzymane wcześniej równanie podzielmy obustronnie przez , stąd , zatem lub . Wiemy, że , stąd ostatecznie
Walec wpisano w stożek. Długość promienia podstawy stożka wynosi . Stosunek objętości walca do objętości stożka wynosi . Obliczmy długość promienia walca.
Rozwiązanie:
Wykreślamy przekrój osiowy tych brył.
– długość promienia podstawy walca;
– długość wysokości walca;
– długość promienia podstawy stożka;
– długość wysokości stożka.
Z warunków zadania mamy zależność , zatem , stąd , zatem .
Zauważmy, że trójkąt jest podobny do trójkąta , stąd mamy zależność , zatem , stąd . Podstawiamy tę zależność do zależności , stąd mamy , po przekształceniach otrzymujemy równanie .
Rozwiązaniami równania są lub , stąd ostatecznie .
Słownik
przekrój stożka płaszczyzną zawierającą oś obrotu stożka; przekrój osiowy stożka jest trójkątem równoramiennym
przekrój walca płaszczyzną zawierającą oś obrotu walca; przekrój osiowy walca jest prostokątem