Przeczytaj

Dwa trójkąty prostokątne mają zawsze jeden kąt taki sam – kąt prosty. Wobec tego w przypadku trójkątów prostokątnych cechy bbb, bkb i kkk podobieństwa trójkątów przyjmują znacznie prostszą postać. Cechy bbb oraz bkb sprowadzają się do jednej cechy.

Odpowiednikiem cech bbb lub bkb może być każde z następujących dwóch twierdzeń.

Trójkąty podobne – porównanie przyprostokątnych

Twierdzenie: Trójkąty podobne – porównanie przyprostokątnych

Jeżeli przyprostokątne jednego trójkąta prostokątnego są proporcjonalne do przyprostokątnych drugiego trójkąta prostokątnego, to te trójkąty są podobne.

R1GLOkJKiH5ix

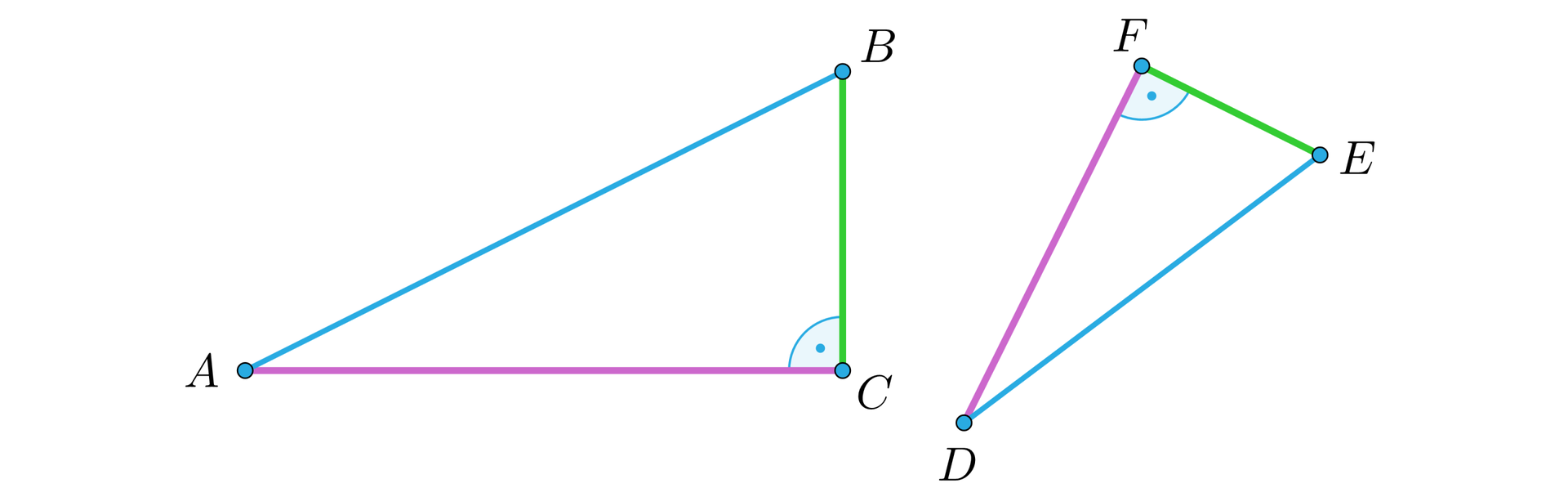
Ilustracja przedstawia dwa trójkąty prostokątne. Pierwszy A B C, drugi D F E. Bok A C jest zaznaczony tym samym kolorem co bok D F. Bok A B jest zaznaczony takim samym kolorem co bok D E. Bok B C jest zaznaczony takim samym kolorem jak bok F E.

Jeżeli $\frac{|A C|}{|B C|} = \frac{|D F|}{|E F|}$ , to trójkąt $A B C$ jest podobny do trójkąta $D E F$ .

Trójkąty podobne – porównanie przeciwprostokątnych

Twierdzenie: Trójkąty podobne – porównanie przeciwprostokątnych

Jeżeli przeciwprostokątna oraz jedna z przyprostokątnych jednego trójkąta prostokątnego są proporcjonalne do przeciwprostokątnej oraz jednej z przyprostokątnych drugiego trójkąta prostokątnego, to te trójkąty są podobne.

R1MJP8WT2gOCd

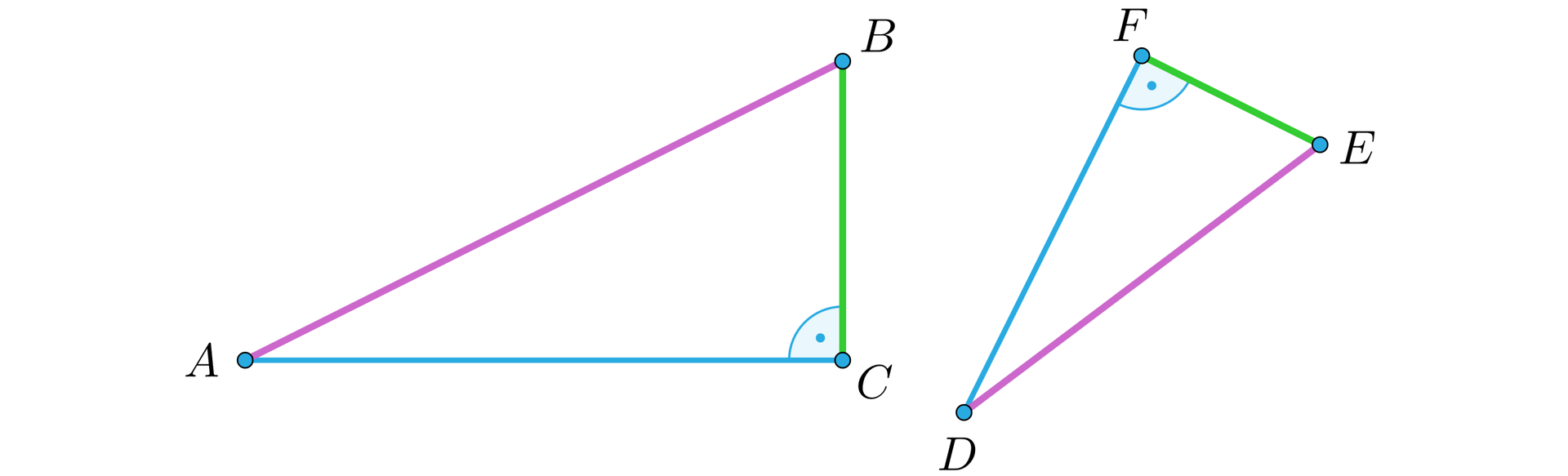
Jeżeli $\frac{|A B|}{|B C|} = \frac{|D E|}{|E F|}$ , to trójkąt $A B C$ jest podobny do trójkąta $D E F$ .

Odpowiednikiem cechy kkk jest następujące twierdzenie.

Trójkąty podobne – porównanie kątów

Twierdzenie: Trójkąty podobne – porównanie kątów

Jeżeli kąt ostry jednego trójkąta prostokątnego jest równy kątowi ostremu drugiego trójkąta prostokątnego, to te trójkąty są podobne.

Rh1z5gKgQL5dj

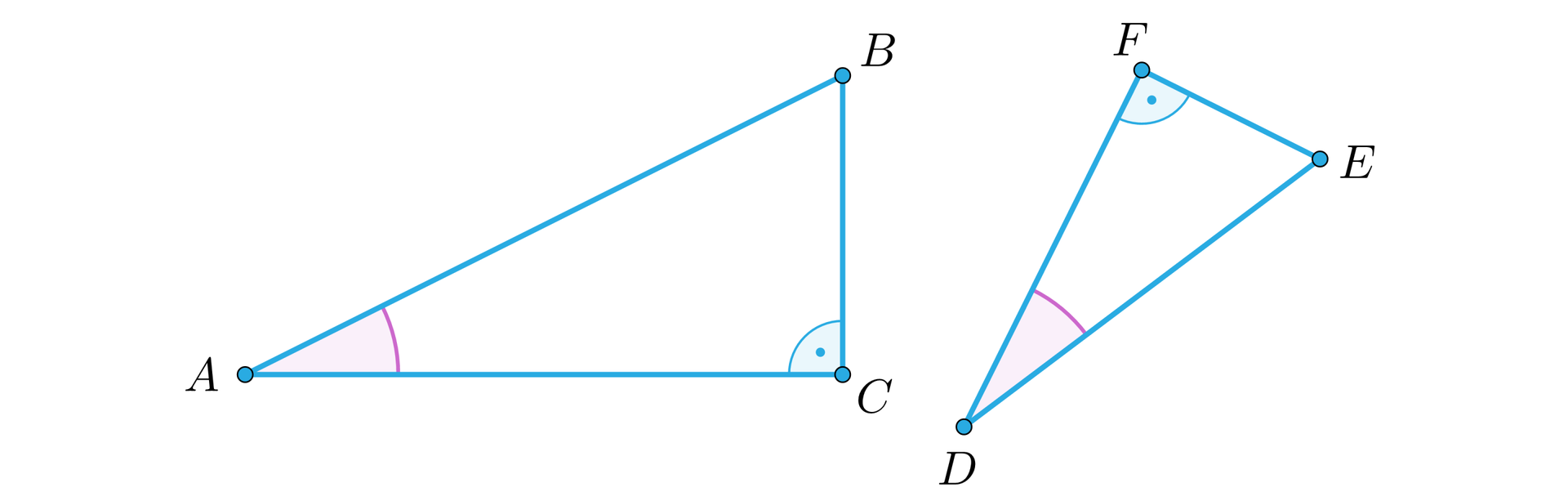
Ilustracja przedstawia dwa trójkąty prostokątne. Pierwszy A B C, drugi D F E. Kąt przy wierzchołku A jest taki sam jak kąt przy wierzchołku D.

Jeżeli $|∢ B A C| = |∢ E D F|$ , to trójkąt $A B C$ jest podobny do trójkąta $D E F$ .

Przykład 1

Rozstrzygniemy, czy trójkąty są podobne.

Przypadek $I$ :
R16LUSNrNaLD7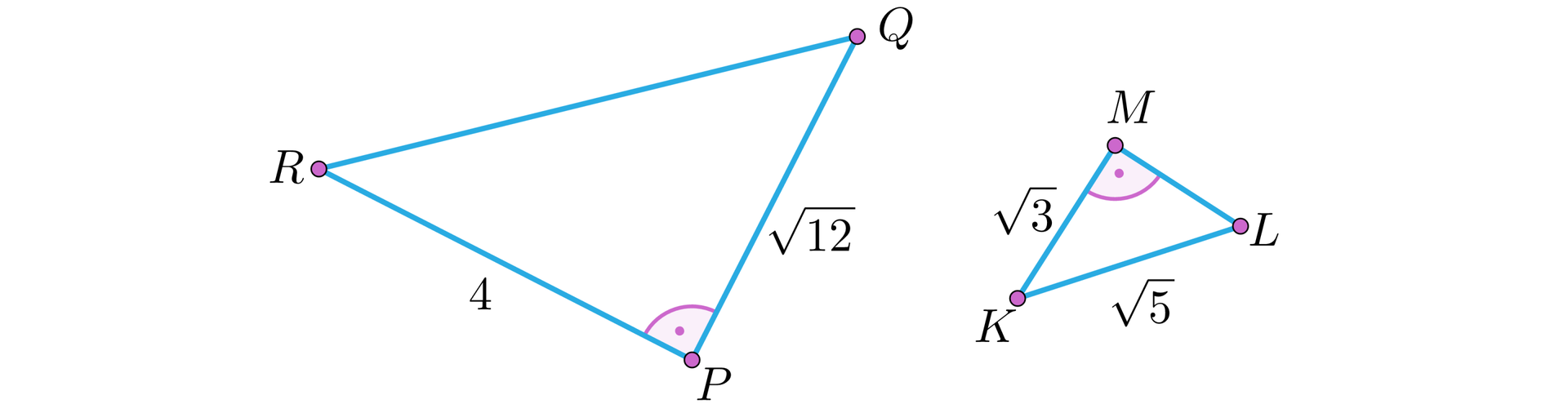
Rozwiązanie:
Z twierdzenia Pitagorasa dla trójkąta $P Q R$ otrzymujemy
$|Q R| = \sqrt{{|P R|}^{2} + {|P Q|}^{2}} = \sqrt{4^{2} + {(\sqrt{12})}^{2}} = \sqrt{16 + 12} = \sqrt{28} = 2 \sqrt{7}$ .
W trójkącie $K L M$ obliczmy stosunek długości przyprostokątnej $K M$ do długości przeciwprostokątnej $K L$ .
Jest on równy $\frac{|K M|}{|K L|} = \frac{\sqrt{3}}{\sqrt{5}} = \frac{\sqrt{15}}{5}$ .
W trójkącie $P Q R$ stosunki długości obu przyprostokątnych do długości przeciwprostokątnej są równe $\frac{|P R|}{|Q R|} = \frac{4}{2 \sqrt{7}} = \frac{\sqrt{14}}{7}$ oraz $\frac{|P Q|}{|Q R|} = \frac{\sqrt{12}}{2 \sqrt{7}} = \frac{2 \sqrt{3}}{2 \sqrt{7}} = \frac{\sqrt{21}}{7}$ .
Ponieważ $\frac{\sqrt{14}}{7} \neq \frac{\sqrt{15}}{5}$ i $\frac{\sqrt{21}}{7} \neq \frac{\sqrt{15}}{5}$ , więc trójkąty $P Q R$ i $K L M$ nie są podobne.
Przypadek $II$ :
R1ZmI0VKCYn0v
Rozwiązanie:
Wyznaczymy kąt ostry przy wierzchołku $B$ w trójkącie $A B C$ .
$|∢ A B C| = 90 ° - |∢ B A C| = 90 ° - 35 ° = 55 °$
Ponieważ kąty ostre przy wierzchołkach $B$ i $F$ w trójkątach prostokątnych $A B C$ i $E G F$ są równe, więc te trójkąty są podobne.

Przykład 2

Trójkąt $A B C$ jest prostokątny. Punkt $D$ jest spodkiem wysokości $C D$ opuszczonej z wierzchołka kąta prostego tego trójkąta.

ReydsTNCPTVED

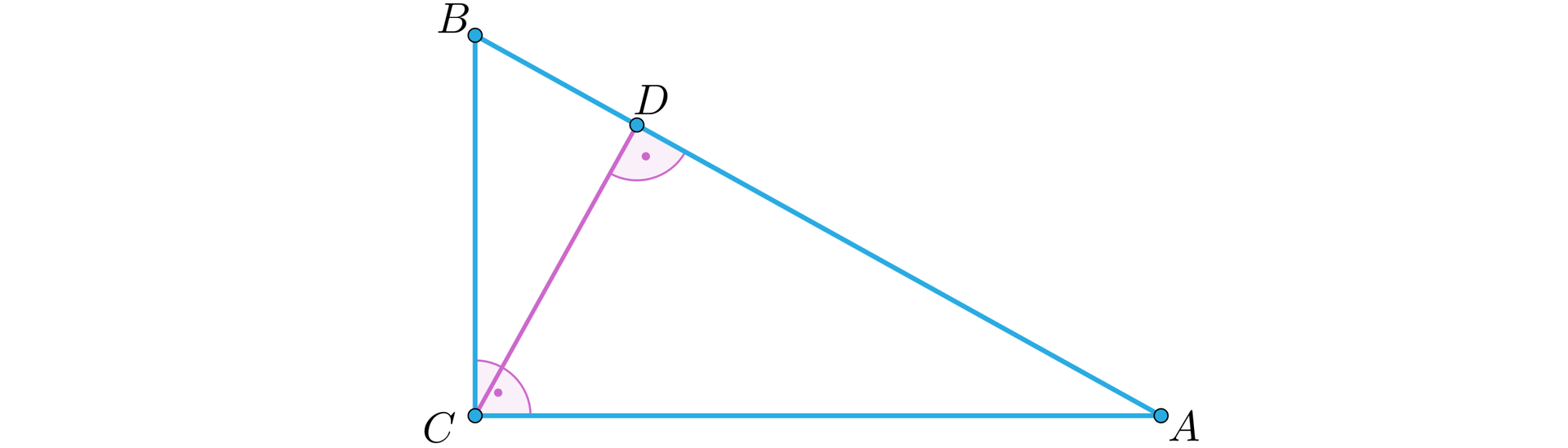
Ilustracja przedstawia trójkąt prostokątny A B C. Kąt przy wierzchołku C jest prosty. Z wierzchołka C upuszczono wysokość na przeciwprostokątną A B. Na przeciwprostokątnej powstał punkt D.

Wykażemy, że: $|C D| = \sqrt{|A D| \cdot |B D|}$ .

Własność tę nazywamy twierdzeniem o wysokości trójkąta prostokątnego opuszczonej na przeciwprostokątną. Możemy ją sformułować następująco:

Długość wysokości trójkąta prostokątnego opuszczonej na przeciwprostokątną jest średnią geometryczną długości odcinków, na jakie spodek tej wysokości dzieli przeciwprostokątną tego trójkąta.

Rozwiązanie:

Trójkąty $A B C$ i $A C D$ są podobne, gdyż oba są prostokątne i mają wspólny kąt ostry przy wierzchołku $A$ .

Trójkąty $A B C$ i $C B D$ też są podobne, bo oba są prostokątne i mają wspólny kąt ostry przy wierzchołku $B$ . Zatem trójkąty $A C D$ i $C B D$ są podobne.

Z tego podobieństwa wynika, że $\frac{|C D|}{|A D|} = \frac{|B D|}{|C D|}$ .

Stąd ${|C D|}^{2} = |A D| \cdot |B D|$ , zatem $|C D| = \sqrt{|A D| \cdot |B D|}$ .

To kończy dowód.

Zauważmy ponadto, że w trójkącie $A B C$ :

R5FrenBTNPKlx

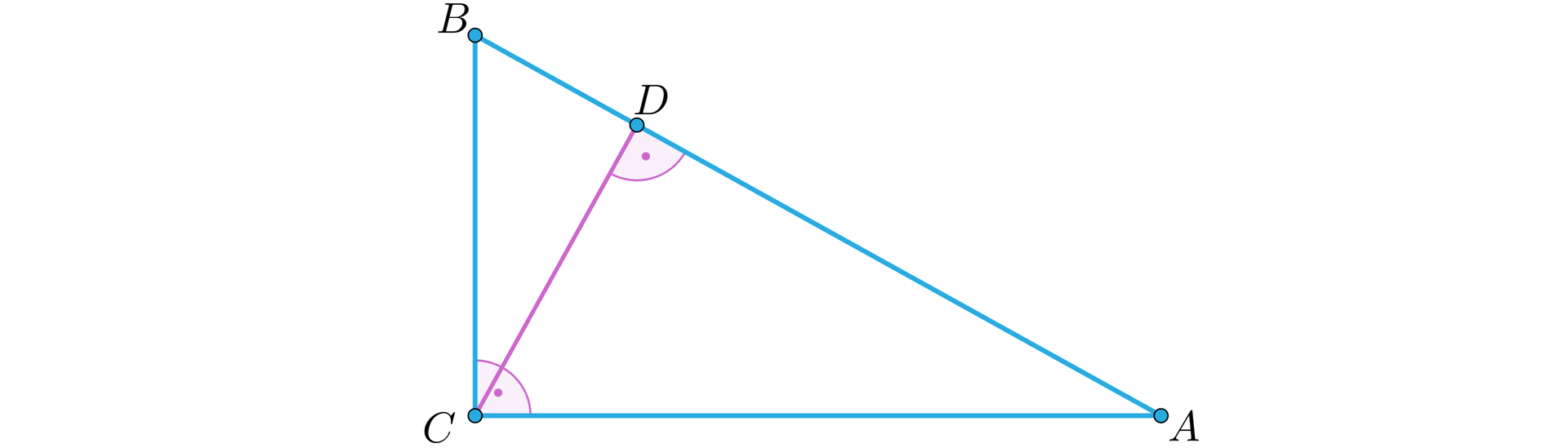
zachodzą również następujące związki:

${|A C|}^{2} = |A B| \cdot |A D|$
${|B C|}^{2} = |A B| \cdot |B D|$

Rzeczywiście:

z podobieństwa trójkątów $A B C$ i $A C D$ wynika, że $\frac{|A C|}{|A B|} = \frac{|A D|}{|A C|}$ , co daje ${|A C|}^{2} = |A B| \cdot |A D|$
z podobieństwa trójkątów $A B C$ i $C B D$ wynika, że $\frac{|B C|}{|A B|} = \frac{|B D|}{|B C|}$ , co daje ${|B C|}^{2} = |A B| \cdot |B D|$

Przykład 3

W trapezie prostokątnym przekątne przecinają się pod kątem prostym. Wykaż, że wysokość tego trapezu jest średnią geometrycznąśrednia geometrycznaśrednią geometryczną długości jego podstaw.

Rozwiązanie:

Przyjmijmy oznaczenia jak na rysunku.

R1LacCd0znFFm

Ilustracja przedstawia trapez prostokątny A B C D. Dłuższa, dolna podstawa A B ma długość a, górna podstawa D C ma długość b. Odcinek A D ma miarę h i jest wysokością trapezu. Trapez posiada dwie przekątne A C oraz B D. Przecinają się pod kątem 90 stopni i tworzą punkt S.

Wówczas tezę możemy zapisać w postaci $h = \sqrt{a \cdot b}$ .

Trójkąty prostokątne $A C D$ i $A D S$ mają wspólny kąt ostry przy wierzchołku $A$ , więc są to trójkąty podobne.

Trójkąty prostokątne $A D S$ i $B D A$ mają wspólny kąt ostry przy wierzchołku $D$ , więc również są to trójkąty podobne.

Stąd wynika, że trójkąt $A C D$ jest podobny do trójkąta $B D A$ .

Zatem $\frac{|D C|}{|A D|} = \frac{|A D|}{|A B|}$ , czyli $\frac{b}{h} = \frac{h}{a}$ . Stąd $h^{2} = a \cdot b$ , więc $h = \sqrt{a \cdot b}$ .

To kończy dowód.

Przykład 4

W trójkącie prostokątnym $A B C$ poprowadzono wysokość $C D$ opuszczoną na przeciwprostokątną $A B$ . Na przyprostokątnych $A C$ i $B C$ obrano takie punkty – odpowiednio – $E$ i $F$ , że czworokąt $C E D F$ jest prostokątem (zobacz rysunek). Pola trójkątów $A D E$ i $C D F$ są równe odpowiednio $16$ i $9$ .

RPDwawEnrDJgm

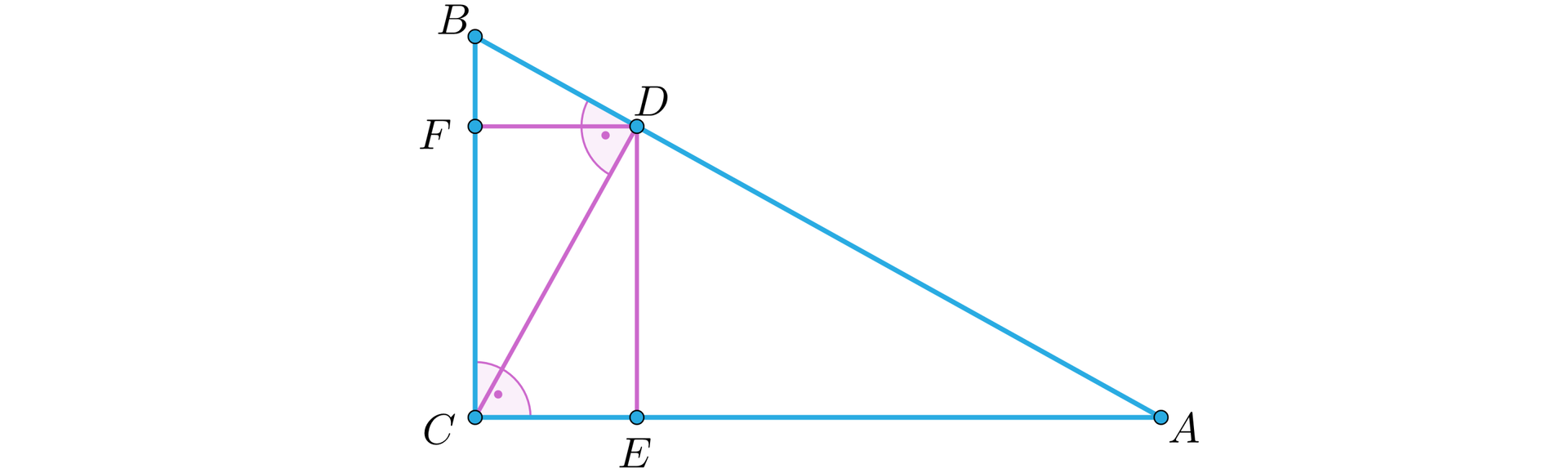
Oblicz pole trójkąta $A B C$ .

Rozwiązanie:

Trójkąty $A B C$ i $D B F$ są podobne, gdyż oba są prostokątne i mają równe kąty ostre przy wierzchołkach $A$ i $D$ .

Równość kątów $E A D$ i $F D B$ wynika z twierdzenia o kątach odpowiadających.

Trójkąty $D C E$ i $C D F$ są przystające, gdyż czworokąt $C E D F$ jest prostokątem, więc $|C E| = |F D|$ i $|D E| = |F C|$ , a bok $C D$ jest wspólnym bokiem tych trójkątów (cecha bbb).

Zatem $P_{D C E} = P_{C D F} = 9$ .

Trójkąty $C D E$ i $A D E$ mają wspólną wysokość $D E$ , więc stosunek pól tych trójkątów jest równy stosunkowi długości ich podstaw, czyli $\frac{|C E|}{|A E|} = \frac{9}{16}$ , ale $|C E| = |F D|$ , więc $\frac{|F D|}{|A E|} = \frac{9}{16}$ .

Stosunek $\frac{|F D|}{|A E|}$ to skala podobieństwa trójkąta $D B F$ do trójkąta $A B C$ , więc z twierdzenia o stosunku pól figur podobnych otrzymujemy $\frac{P_{D B F}}{P_{A D E}} = {(\frac{9}{16})}^{2}$ , czyli $\frac{P_{D B F}}{16} = {(\frac{9}{16})}^{2}$ .

Stąd $P_{D B F} = \frac{81}{16}$ . Wobec tego $P_{A B C} = P_{D B F} + 2 P_{C D F} + P_{A D E} = \frac{81}{16} + 2 \cdot 9 + 16 = 39 \frac{1}{16}$ .

Przykład 5

Na przyprostokątnych $A C$ i $B C$ trójkąta prostokątnego $A B C$ zbudowano, na zewnątrz tego trójkąta, kwadraty $A C D E$ i $B C E F$ . Odcinki $B E$ i $A C$ przecinają się w punkcie $K$ , a odcinki $A F$ i $B C$ przecinają się w punkcie $L$ (zobacz rysunek).

RtzMjXcabPYD4

Ilustracja przedstawia trójkąt prostokątny A B C . Na przyprostokątnej A C i B C trójkąta zbudowano, na zewnątrz trójkąta kwadraty A C D E i B C E D. Odcinki BE i A C przecinają się w punkcie K, a odcinki A F i B C przecinają się w punkcie L.

Udowodnij, że $|K C| = |L C|$ .

Rozwiązanie:

Niech $|A C| = b$ oraz $|B C| = a$ .

Czworokąty $A C D E$ i $B C E F$ to kwadraty, więc $|A C| = |C D| = |D E| = b$ oraz $|B C| = |C E| = |E F| = a$ .

Trójkąty $A F E$ i $A L C$ są podobne, gdyż oba są prostokątne i mają wspólny kąt ostry przy wierzchołku $A$ .

Tak samo trójkąty $B D E$ i $B C K$ są podobne, gdyż oba są prostokątne i mają wspólny kąt ostry przy wierzchołku $B$ .

Z tych podobieństw wynika, że

$\frac{|C L|}{|A C|} = \frac{|E F|}{|A E|}$ oraz $\frac{|K C|}{|B C|} = \frac{|D E|}{|B D|}$ , czyli $\frac{|C L|}{b} = \frac{a}{a + b}$ oraz $\frac{|K C|}{a} = \frac{b}{a + b}$ .

Stąd $|C L| = \frac{a b}{a + b}$ oraz $|K C| = \frac{a b}{a + b}$ . Zatem $|K C| = |L C|$ .

To kończy dowód.

Słownik

średnia geometryczna

średnią geometryczną dwóch liczb nieujemnych $x$ i $y$ nazywamy liczbę $\sqrt{x \cdot y}$ ; średnią geometryczną $n$ liczb nieujemnych $x_{1}$ , $x_{2}$ , $x_{3}$ , $. . .$ , $x_{n}$ nazywamy liczbę $\sqrt[n]{x_{1} \cdot x_{2} \cdot x_{3} \cdot . . . \cdot x_{n}}$

Wprowadzenie

Aplet

Słownik