Zacznijmy od problemu geometrycznego: Czy istnieje na płaszczyźnie trójkąt, w którym przynajmniej jedna dwusieczna kąta jest jednocześnie środkową boku?

Rozwiązanie

Oczywiście, od razu powiesz, że w trójkącie równobocznym dwusieczne wszystkich kątów są środkowymi boków. Masz rację. Ale zgłębiając dalej problem możemy zadać sobie kolejne pytanie: Czy istnieje inne rozwiązanie?

I znowu, korzystając z już nabytej wiedzy z geometrii, odpowiesz: w każdym trójkącie równoramiennym, ale nierównobocznym, istnieje jedna dwusieczna kąta, która jest jednocześnie środkową boku. To jest prawda, ale przecież istnieją inne trójkąty niż równoramienne i równoboczne. Ponawiamy więc pytanie: Czy istnieje inne rozwiązanie?

Udowodnimy, że nie istnieje inne rozwiązanie postawionego problemu na płaszczyźnie, to znaczy udowodnijmy twierdzenie:

w trójkącie różnobocznym żadna dwusieczna kąta nie jest jednocześnie środkową boku.

Założenie: trójkąt jest trójkątem różnobocznym

Teza: żadna dwusieczna kąta nie jest jednocześnie środkową boku w tym trójkącie

Ponieważ trudno jest tutaj zacząć dowód od przekształcania założenia (trójkątów różnobocznych jest nieskończenie wiele i niemożliwe jest rozpatrzenie każdego z nich), więc udowodnimy twierdzenie metodą nie wprost.

Twierdzenie zapisane w postaci kontrapozycji ma postać:

jeżeli co najmniej jedna dwusieczna kąta w trójkącie jest środkową przeciwległego boku, to trójkąt nie jest różnoboczny.

Dowód:

Wykonujemy rysunek pomocniczy:

Konstruujemy kąt, jego dwusieczną i obieramy dowolny punkt na dwusiecznej (z wyjątkiem wierzchołka kąta). Konstruujemy prostopadłą do dwusiecznej przechodzącą przez wybrany punkt. Otrzymaliśmy trójkąt równoramienny $ABC$:

R1QA0wWWVic54

Na ilustracji przedstawiono kąt o wierzchołku C, którego ramiona przechodzą przez punkty A i B. Po połączeniu punktów A i B powstał trójkąt równoramienny. Zaznaczono kąty alfa przy wierzchołku A, oraz B. Z wierzchołka C opuszczono dwusieczną kąta $ACB$ do podstawy trójkąta $AB$ w punkcie D.

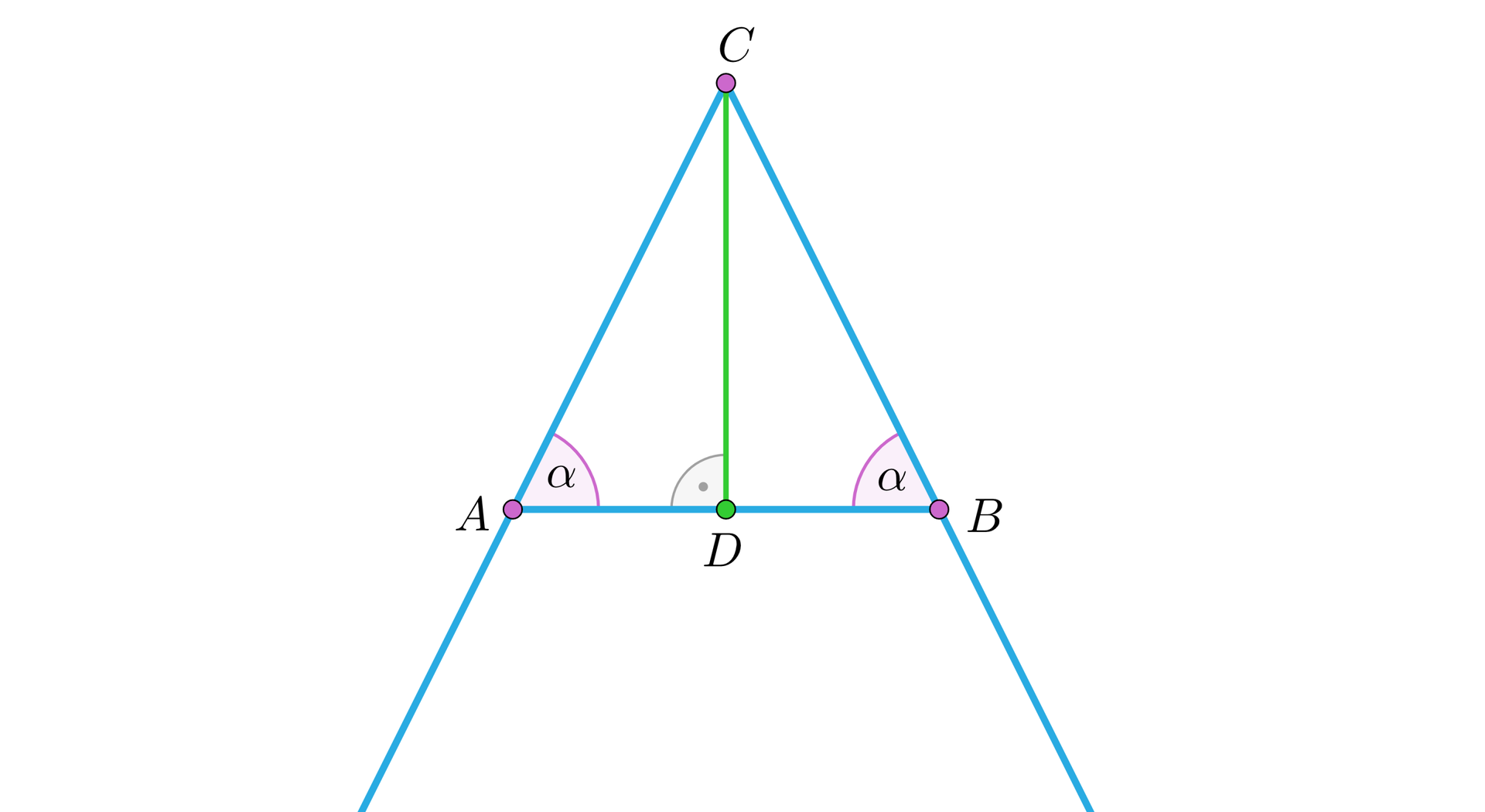
Załóżmy, że jest możliwe, aby dwusieczna kąta w trójkącie różnobocznym była jednocześnie środkową przeciwległego boku. Przeprowadźmy przez punkt $D$ na dwusiecznej prostą, która nie jest prostopadła do dwusiecznej. Otrzymaliśmy trójkąt różnoboczny $EFC$:

R6KqMQrdgsctA

Na ilustracji przedstawiono kąt o wierzchołku C, którego ramiona przechodzą przez punkty A i B. Po połączeniu punktów A i B powstał trójkąt równoramienny. Zaznaczono kąty alfa przy wierzchołku A, oraz B. Z wierzchołka C opuszczono dwusieczną kąta $ACB$ do podstawy trójkąta $AB$ w punkcie D. Na ramieniu $BC$ zaznaczono punkt F. Narysowano prostą przechodzącą przez punkt F, D, oraz przecinającą przeciwległe ramię kąta w punkcie E.

Jeżeli nasza dwusieczna ma być środkową boku, to odcinki ED i DF powinny być równej długości. Czy są? Jak to sprawdzić?

Spójrzmy na te odcinki jako na boki trójkątów. Czy trójkąty EDA i DBF są przystające?

Pamiętamy, że dwa trójkąty są przystające, jeżeli mają takie same kąty i takie same boki. W naszym przypadku oznacza to, że dwa kąty przeciwległe do boków $ED$ i $DF$ powinny być takie same. Korzystamy tu z cechy przystawania trójkątów kąt‑bok‑kąt, mając równość kątów wierzchołkowych $BDF$ i $ADE$ oraz równość odcinków $AD$ i $DB$. Równość kątów $EAD$ i $DBF$ oznaczałaby, że kąty oznaczone powinny mieć miary po $90°$, gdyż dwa kąty $\alpha$ (jak na rysunku) tworzą kąt półpełny.

RveIvDMwaynYd

Na ilustracji przedstawiono kąt o wierzchołku C, którego ramiona przechodzą przez punkty A i B. Po połączeniu punktów A i B powstał trójkąt równoramienny. Zaznaczono kąty alfa przy wierzchołku A, oraz B. Z wierzchołka C opuszczono dwusieczną kąta $ACB$ do podstawy trójkąta $AB$ w punkcie D. Na ramieniu $BC$ zaznaczono punkt F. Narysowano prostą przechodzącą przez punkt F, D, oraz przecinającą przeciwległe ramię kąta w punkcie E. Kąty $BDF$, oraz $EDA$ oznaczono beta.

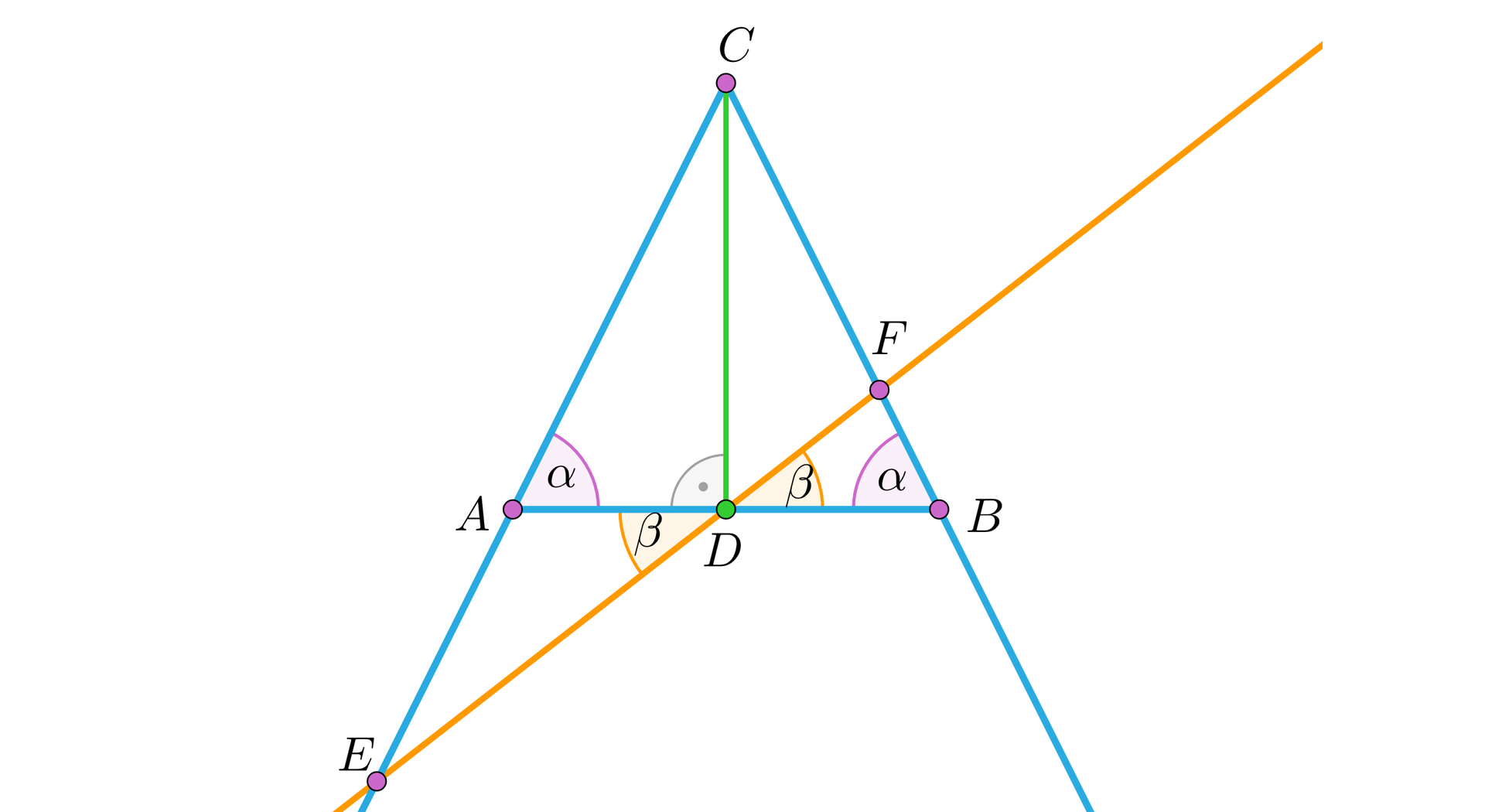
Ale wtedy ramiona kątów powinny być równoległe do siebie. To jest niemożliwe, ponieważ nie istniałby wtedy trójkąt.

RkIjBeXZVEoJb

Na ilustracji przedstawiono kąt o wierzchołku C, którego ramiona przechodzą przez punkty A i B. Po połączeniu punktów A i B powstał trójkąt równoramienny. Zaznaczono kąty alfa przy wierzchołku A, oraz B. Z wierzchołka C opuszczono dwusieczną kąta $ACB$ do podstawy trójkąta $AB$ w punkcie D. Na ramieniu $BC$ zaznaczono punkt F. Narysowano prostą przechodzącą przez punkt F, D, oraz przecinającą przeciwległe ramię kąta w punkcie E. Kąty $BDF$, oraz $EDA$ oznaczono beta. Przez punkt A, oraz B poprowadzono przerywane linie, równoległe do siebie.

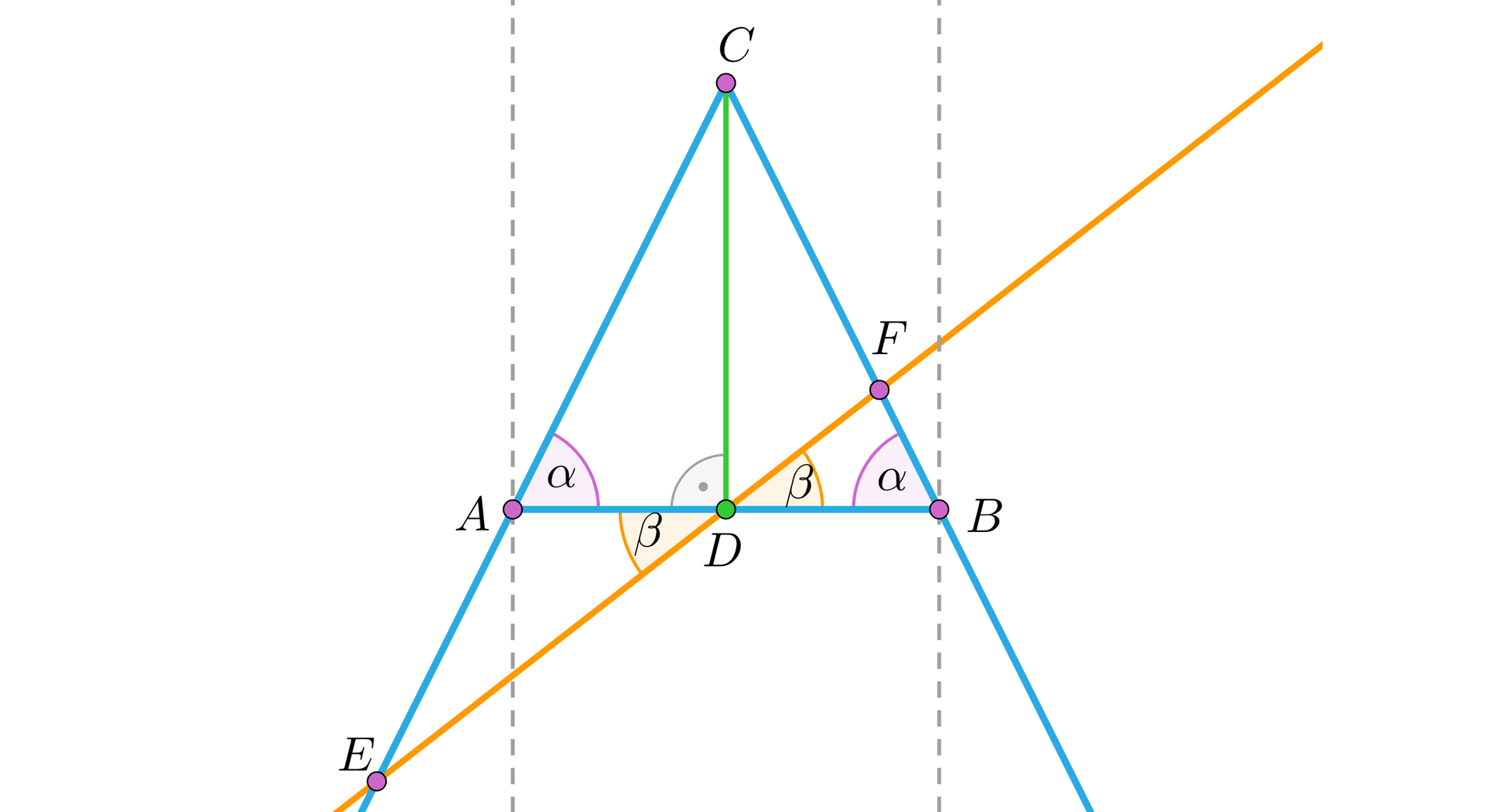
Pokazaliśmy, że gdyby w trójkącie różnobocznym dwusieczna kąta była środkową przeciwległego boku, to nasz trójkąt nie byłby trójkątem! Tak więc – zgodnie z określeniem dowodu nie wprost: „zaprzeczenie tezy prowadzi do wniosku sprzecznego z założeniem, bądź też z jakimś twierdzeniem prawdziwym” – wychodząc od zaprzeczenia tezy pokazaliśmy sprzeczność z warunkami istnienia trójkąta (w trójkącie na płaszczyźnie nie mogą istnieć dwa kąty proste).

c.n.d.

Udowodnimy, że jeżeli $m>0$, to $m+\frac{4}{m^2}\ge 3$.

Rozwiązanie

Założenie: $m>0$

Teza: $m+\frac{4}{m^2}\ge 3$

Zaprzeczenie założenia: $m\le 0$

Zaprzeczenie tezy: $m+\frac{4}{m^2}<3$

Prowadzimy dowód nie wprostdowód nie wprostdowód nie wprost, czyli dowodzimy twierdzenie zapisane w postaci kontrapozycji:

Jeśli $m+\frac{4}{m^2}<3$ to $m\le 0$

Dowód:

Przekształcamy nierówność:

$m+\frac{4}{m^2}<3$

$m^3+4<3m^2$

$m^3–3m^2+4<0$

$m^3+m^2-4m^2+4<0$

$m^2\left(m+1\right)-4\left(m^2-1\right)<0$

$m^2\left(m+1\right)-4\left(m-1\right)\left(m+1\right)<0$

$\left(m+1\right)\left(m^2-4m+4\right)<0$

$\left(m+1\right){\left(m-2\right)}^2<0$

Aby powyższa nierówność była prawdziwa, musi być spełniona nierówność $m+1<0$, czyli $m<-1$.

Powyższa nierówność nie może być spełniona dla żadnej liczby $m$ dodatniej. Udowodniliśmy, że zaprzeczenie tezy naszego twierdzenia prowadzi do zaprzeczenia założenia, a więc twierdzenie

Jeżeli $m>0$, to $m+\frac{4}{m^2}\ge 3$.

jest prawdziwe.

c.n.d.

Udowodnimy, że suma liczby wymiernej i liczby niewymiernej jest liczbą niewymierną.

Twierdzenie brzmi: Niech $a$ będzie liczbą wymierną i $b$ liczbą niewymierną. Wówczas suma $a+b$ jest liczbą niewymierną.

Rozwiązanie

Założenie: $a$ jest liczbą wymierną, $b$ jest liczbą niewymierną

Teza: $a+b$ jest liczbą niewymierną

Dowód metodą nie wprost:

Załóżmy, że suma $a+b$ jest liczbą wymierną. Możemy wtedy zapisać (zgodnie z określeniem liczby wymiernej): $a+b=\frac{m}{n}$, gdzie $m$ i $n$ to liczby całkowite, przy czym $n\ne 0$. Z założenia wiemy, że $a$ jest liczbą wymierną, więc możemy zapisać: $a=\frac{p}{q}$, gdzie $p$ i $q$ to liczby całkowite, przy czym $q\ne 0$. Tak więc

$b=\left(a+b\right)-a=\frac{m}{n}-\frac{p}{q}=\frac{mq-pn}{nq}$

Licznik i mianownik tego ułamka są liczbami całkowitymi, mianownik jest liczbą różną od zera jako iloczyn liczb różnych od zera, więc $b$ jest liczbą wymierną, co stanowi sprzeczność z założeniem, że liczba $b$ jest liczbą niewymierną.

Tak więc zaprzeczając tezie i doprowadzając do sprzeczności z założeniem udowodniliśmy nasze twierdzenie wyjściowe.

Udowodnimy twierdzenie: Niech $n$ będzie liczbą całkowitą. Jeśli $n^2$ jest liczbą nieparzystą, to $n$ jest liczbą nieparzystą.

Rozwiązanie

Założenie: $n^2$ jest liczbą nieparzystą

Teza: $n$ jest liczbą nieparzystą

Twierdzenie w postaci kontrapozycjitwierdzenie w postaci kontrapozycjiTwierdzenie w postaci kontrapozycji:

Niech $n$ będzie liczbą całkowitą. Jeśli $n$ jest liczbą parzystą, to $n^2$ jest liczbą parzystą.

Dowód:

Zanegujmy tezę, czyli załóżmy, że $n$ jest liczbą parzystą. Wówczas możemy zapisać, że $n=2k$ dla jakiejś liczby całkowitej $k$. Stąd $n^2={\left(2k\right)}^2=4k^2=2·2k^2$, czyli liczba $n^2$ jest liczbą parzystą, co przeczy założeniu twierdzenia. Tak więc dowodząc twierdzenia w formie kontrapozycji udowodniliśmy twierdzenie wyjściowe.

Udowodnimy, że $\cos 10°$ jest liczbą niewymierną.

Rozwiązanie

Załóżmy, że $\cos 10°$ jest liczbą wymierną, czyli możemy zapisać: $\cos \left(10°\right)=\frac{m}{n}$, gdzie $m$ i $n$ to liczby całkowite, przy czym $n\ne 0$. Skorzystajmy ze wzoru na cosinus kąta potrojonego i zapiszmy:

$\cos \left(30°\right)=\cos \left(3·10°\right)=4\cos {\left(10°\right)}^3-3\cos \left(10°\right)=4{\left(\frac{m}{n}\right)}^3-\frac{3m}{n}=$

$=\frac{4m^3-3m{n}^2}{n^3}=\frac{p}{q}$

gdzie $p$ i $q$ to liczby całkowite, przy czym $q\ne 0$, czyli $\cos 30°$ jest liczbą wymierną.

Wiemy jednak, że $\cos \left(30°\right)=\frac{\sqrt{3}}{2}$, czyli jest liczbą niewymierną. Tak więc zaprzeczając tezie doszliśmy do sprzeczności z dobrze nam znanym faktem matematycznym. Tym samym udowodniliśmy nasze twierdzenie wyjściowe.

zdanie złożone mające postać „jeśli $p$ to $q$”, gdzie $p$, $q$ są zdaniami logicznymi

zdanie oznajmujące złożone z dwóch zdań, przy czym jedno wynika z drugiego

równoważność implikacji prostej i przeciwstawnej, czyli $\left(p\Rightarrow q\right)\iff \left(~q\Rightarrow ~p\right)$

dla danego twierdzenia to zdanie orzekające wynikanie zaprzeczenia założenia z zaprzeczenia tezy

dowód polegający na wykazaniu, że zaprzeczenie tezy prowadzi do wniosku sprzecznego z założeniem, bądź też z jakimś twierdzeniem prawdziwym