Przeczytaj

Poniższe twierdzenie, zwane jedynką trygonometryczną, pokazuje związek między sinusemsinus kąta ostregosinusem i cosinusemcosinus kąta ostregocosinusem kąta ostrego. Jest to inne wysłowienie twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa.

Jedynka trygonometryczna

Twierdzenie: Jedynka trygonometryczna

Dla każdego kąta ostrego $α$ prawdziwa jest zależność:

$\sin^{2} α + \cos^{2} α = 1$ .

Dowód

Przy oznaczeniach z rysunku obok mamy:

$\sin^{2} α + \cos^{2} α = {(\frac{a}{c})}^{2} + {(\frac{b}{c})}^{2} = \frac{a^{2} + b^{2}}{c^{2}} = \frac{c^{2}}{c^{2}} = 1$ ,

RONCFCJAyIx7q1

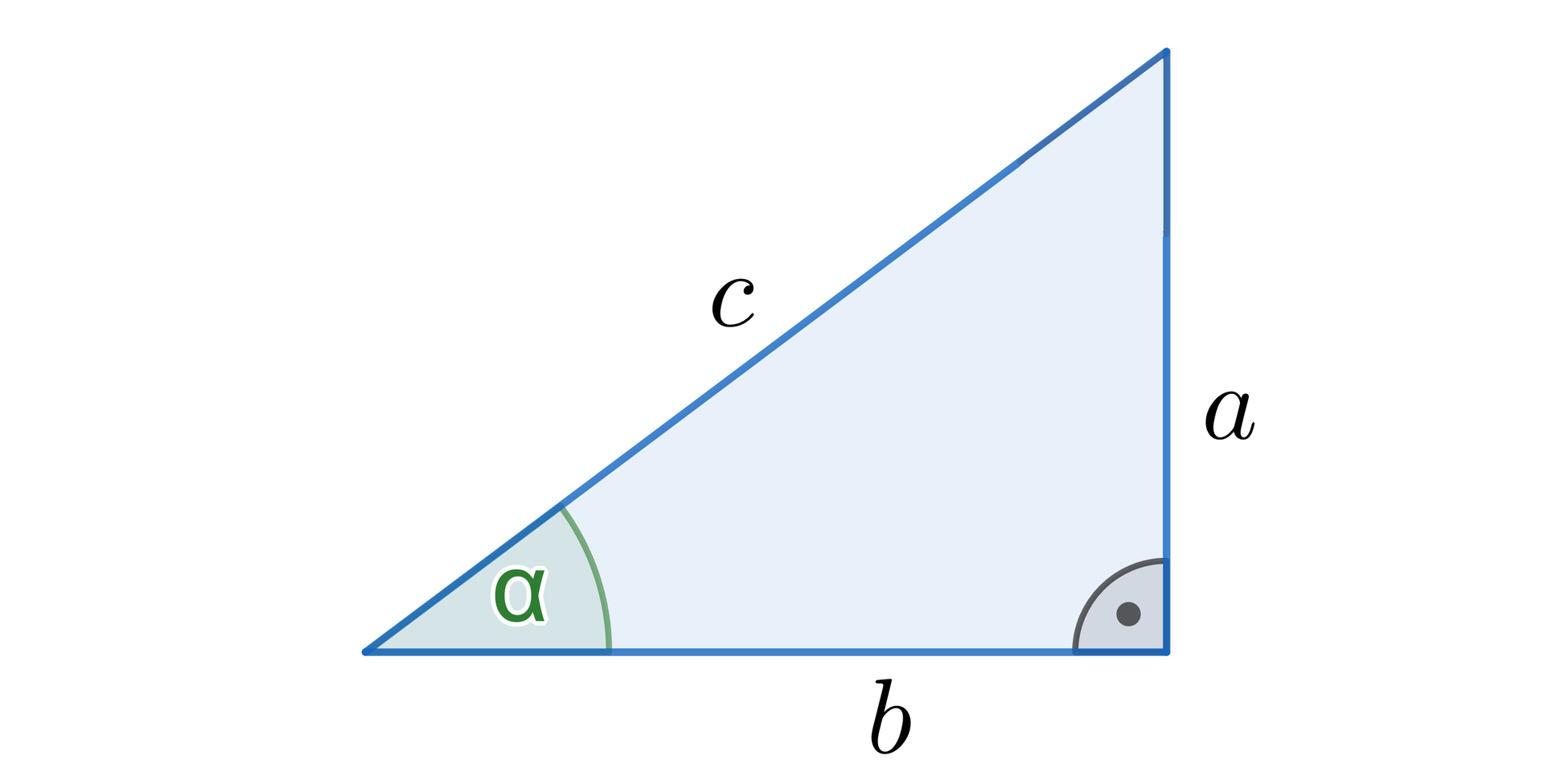
Ilustracja przedstawia trójkąt prostokątny, jego pionowa przyprostokątna jest podpisana literą a, jego pozioma przyprostokątna jest podpisana literą b, a jego przeciwprostokątna jest podpisana literą c. Kąt pomiędzy przeciwprostokątną a przyprostokątną b jest podpisana literą alfa.

bowiem

$a^{2} + b^{2} = c^{2}$

na mocy twierdzenia Pitagorasa.

Przykład 1

Sinus kąta $α$ w trójkącie prostokątnym jest równy $\frac{5}{13}$ . Wyznaczymy wartość cosinusa tego kąta.

Rozwiązanie

Wiemy, że: $\sin^{2} α + \cos^{2} α = 1$ , więc: $\cos^{2} α = 1 - \sin^{2} α = 1 - {(\frac{5}{13})}^{2} = 1 - (\frac{25}{169}) = (\frac{144}{169}) = {(\frac{12}{13})}^{2} .$

Cosinus kąta ostrego jest dodatni, zatem $\cos α = \frac{12}{13} .$

Zależność między funkcjami

\sin

\cos

tg

tego samego kąta

Twierdzenie: Zależność między funkcjami

\sin

\cos

tg

tego samego kąta

Dla każdego kąta ostrego $α$ w trójkącie prostokątnym zachodzi zależność:

$\frac{\sin α}{\cos α} = tg α$

Dowód. Przy oznaczeniach z poprzedniego rysunku mamy:

$\frac{\sin α}{\cos α} = (\frac{\frac{a}{c}}{\frac{b}{c}}) = \frac{a}{c} \cdot \frac{c}{b} = \frac{a}{b} = tg α$ .

Przykład 2

Wiemy, że sinus kąta $α$ w trójkącie prostokątnym jest równy $\frac{3}{5}$ . Wyznaczymy wartość tangensatangens kąta ostregotangensa tego kąta.

Rozwiązanie

Korzystając z jedynki trygonometrycznej, obliczamy: $\cos^{2} α = 1 - \sin^{2} α = 1 - {(\frac{3}{5})}^{2} = \frac{16}{25} = {(\frac{4}{5})}^{2}$ .

Cosinus kąta ostrego jest dodatni, zatem $\cos α = \frac{4}{5} .$

Wobec tego:

$tg α = \frac{\sin α}{\cos α} = \frac{3}{5} : \frac{4}{5} = \frac{3}{4}$ .

Bezpośrednio z definicji sinusa, cosinusa i tangensa skorzystamy w dowodzie następnego twierdzenia.

Wzory redukcyjne

Twierdzenie: Wzory redukcyjne

Dla każdego kąta ostrego $α$ w trójkącie prostokątnym zachodzą równości: $\sin (90 ° - α) = \cos α$ oraz $\cos (90 ° - α) = \sin α$ . Ponadto: $tg (90 ° - α) = \frac{1}{tg α}$ .

Dowód

Wprowadźmy oznaczenie: $β = 90^{\circ} - α$ .

REodUNyZ0pDiM1

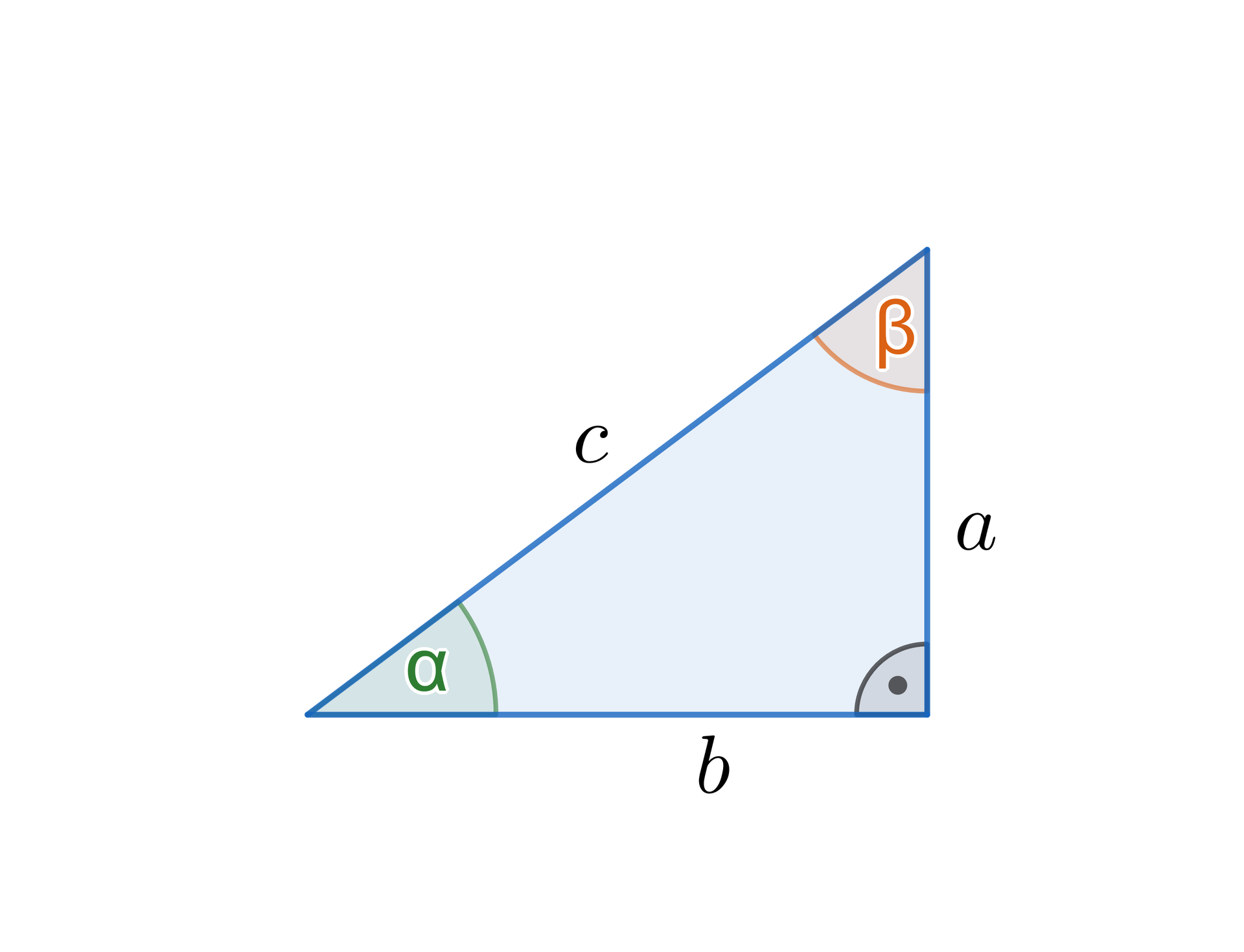
Wtedy przy oznaczeniach z rysunku obok, otrzymujemy:

$\sin β = \frac{b}{c} = \cos α, \cos β = \frac{a}{c} = \sin α$ oraz

$tg β = \frac{b}{a} = \frac{1}{\frac{a}{b}} = \frac{1}{tg α}$ .

Przykład 3

Obliczymy wartość wyrażenia: ${(\cos 53 ° + \cos 37 °)}^{2} - 2 \cdot \sin 53 ° \cdot \sin 37 ° + 3 \cdot tg 53 ° \cdot tg 37 °$ .

Rozwiązanie

Ponieważ $53 ° + 37 ° = 90 °$ , więc zachodzą równości:

$\cos 53 ° = \sin 37 °$ , $\sin 53 ° = \cos 37 °$ oraz $tg 53 ° = \frac{1}{tg 37 °}$ .

Zatem:

${(\cos 53 ° + \cos 37 °)}^{2} - 2 \cdot \sin 53 ° \cdot \sin 37 ° + 3 \cdot tg 53 ° \cdot tg 37 ° =$

$= {(\sin 37 ° + \cos 37 °)}^{2} - 2 \cdot \cos 37 ° \cdot \sin 37 ° + 3 \cdot \frac{1}{tg 37 °} \cdot tg 37 ° =$

$= \sin^{2} 37 ° + 2 \cdot \sin 37 ° \cdot \cos 37 ° + \cos^{2} 37 ° - 2 \cdot \sin 37 ° \cdot \cos 37 ° + 3 \cdot 1 =$

$= 1 + 3 = 4$

Przykład 4

Obliczymy wartość iloczynu $tg 10 ° \cdot tg 40 ° \cdot tg 50 ° \cdot tg 80 ° .$

Rozwiązanie

Ponieważ $80 ° = 90 ° - 10 °$ i $50 ° = 90 ° - 40 °$ , więc:

$tg 80 ° = \frac{1}{tg 10 °}$ i $tg 50 ° = \frac{1}{tg 40 °}$ .

A zatem:

$tg 10 ° \cdot tg 40 ° \cdot tg 50 ° \cdot tg 80 ° = tg 10 ° \cdot tg 40 ° \cdot \frac{1}{tg 40 °} \cdot \frac{1}{tg 10 °} = 1$ .

Przykład 5

Wiedząc, że $α$ jest kątem ostrym i $tg α = 5$ , obliczymy wartość wyrażenia:

$\frac{2 \sin α + 3 \cos α}{4 \sin α - 5 \cos α}$ .

Rozwiązanie

Ponieważ $tg α = \frac{\sin α}{\cos α} = 5$ , więc $\sin α = 5 \cos α$ .

Zatem otrzymujemy:

$\frac{2 \sin α + 3 \cos α}{4 \sin α - 5 \cos α}$ $= \frac{2 \cdot 5 \cos α + 3 \cos α}{4 \cdot 5 \cos α - 5 \cos α} = \frac{13 \cos α}{15 \cos α} = \frac{13}{15}$ .

Ważne!

Tożsamość trygonometryczna to równość, w której zmienne występują wyłącznie w argumentach funkcji trygonometrycznych, prawdziwa dla wszystkich wartości tych zmiennych, dla których funkcje mają sens.

Przykład 6

Wykażemy, że dla dowolnego kąta ostrego $α$ zachodzi tożsamość: ${(\sin α + \cos α)}^{2} + {(\sin α - \cos α)}^{2} = 2$ .

Rozwiązanie

Zapisaną w postaci złożonego wyrażenia lewą stronę równości $(L)$ przekształcamy równoważnie tak, aby dojść do strony prawej $(P)$ .

Przyjmujemy:

$L = {(\sin α + \cos α)}^{2} + {(\sin α - \cos α)}^{2}$ i $P = 2$ .

Mamy: ${(\sin α + \cos α)}^{2} = \sin^{2} α + 2 \sin α \cos α + \cos^{2} α = 1 + 2 \sin α \cos α$ , podobnie:

${(\sin α - \cos α)}^{2} = 1 - 2 \sin α \cos α$ .

Stąd: $L = 1 - 2 \sin α \cos α + 1 + 2 \sin α \cos α = 2$ ,

czyli $L = P$ .

Słownik

sinus kąta ostrego

stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej

cosinus kąta ostrego

stosunek długości przyprostokątnej leżącej przy kącie do długości przeciwprostokątnej

tangens kąta ostrego

stosunek długości przyprostokątnej leżącej naprzeciw tego kąta do długości przyprostokątnej leżącej przy tym kącie

twierdzenie Pitagorasa

jeżeli trójkąt jest prostokątny, to suma kwadratów dwóch długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej

Wprowadzenie

Film samouczek

Słownik