Przeczytaj

Odległość punktu $X$ od płaszczyzny $π$ będziemy oznaczać $d (X, π)$ .

Jeśli punkt $X$ leży na płaszczyźnie $π$ , to jego odległość od tej płaszczyzny jest równa $0$ .

Jeśli punkt $X$ nie leży na płaszczyźnie $π$ , to jego odległość od $π$ jest równa długości najkrótszego odcinka, którego jednym z końców jest $X$ , zaś drugim punkt płaszczyzny $π$ .

R17v1MY8lha03

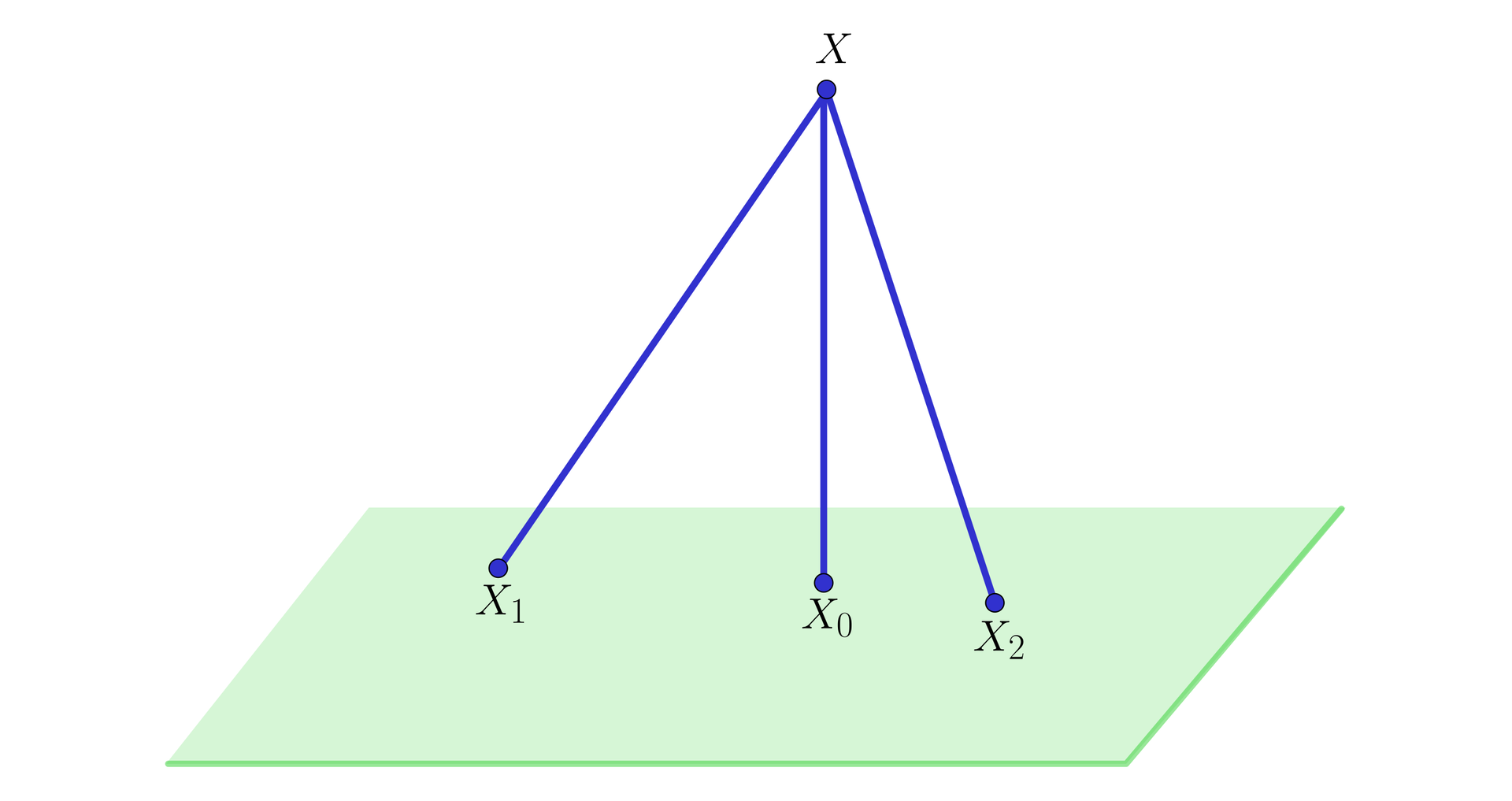
Ilustracja przedstawia płaszczyznę pi oraz punkt X oddalony od tej płaszczyzny. Punkt X został połączony z trzema innymi punktami znajdującymi się na płaszczyźnie pi. Dzięki temu powstały trzy odcinki, odcinek X indeks dolny jeden koniec indeksu X, odcinek X indeks dolny zero koniec indeksu X oraz odcinek X indeks dolny dwa koniec indeksu X.

|X X_{0}| < |X X_{1}|

|X X_{0}| < |X X_{2}|

Łatwo zauważyć, że najkrótszy odcinek łączący $X$ z punktem płaszczyzny $π$ jest do niej prostopadły.

RQEHg5vLarSrw

Ilustracja przedstawia płaszczyznę pi oraz punkt X oddalony od tej płaszczyzny. Na płaszczyźnie pi zaznaczono również dwa punkty, punkt X indeks dolny jeden koniec indeksu oraz punkt X indeks dolny zero koniec indeksu. Wszystkie trzy punkty zostały połączone w taki sposób, że powstał trójkąt prostokątny X indeks dolny zero koniec indeksu, X, X indeks dolny jeden koniec indeksu. Przyprostokątną trójkąta są odcinki X indeks dolny jeden koniec indeksu, X indeks dolny zero koniec indeksu oraz odcinek X indeks dolny zero koniec indeksu X, natomiast odcinek X, X indeks dolny jeden koniec indeksu jest przeciwprostokątną. Wewnątrz trójkąta zaznaczono również kąty alfa i beta. Kąt alfa znajduje się przy wierzchołku X indeks dolny zero koniec indeksu i jest kątem prostym, natomiast kąt beta przy wierzchołku X indeks dolny jeden koniec indeksu.

|X X_{0}| < |X X_{1}|

, bo

β < α

Rozważmy punkty $X_{0}$ oraz $X_{1}$ należące do płaszczyzny $π$ takie, że odcinek $X X_{0}$ jest do niej prostopadły. Wówczas trójkąt $X X_{0} X_{1}$ jest prostokątny i $|∢ X X_{1} X_{0}| < 90 °$ . Ponieważ naprzeciwko kąta o mniejszej mierze leży krótszy bok, więc z tego, że $|∢ X X_{1} X_{0}| < |∢ X X_{0} X_{1}|$ wynika, iż $|X X_{0}| < |X X_{1}|$ .

Przykład 1

Rozważmy prostopadłościan o krawędziach wychodzących z jednego wierzchołka, które mają długości $2$ , $3$ , $4$ i wierzchołkach jak na rysunku.

R1TjPU9h9Quel

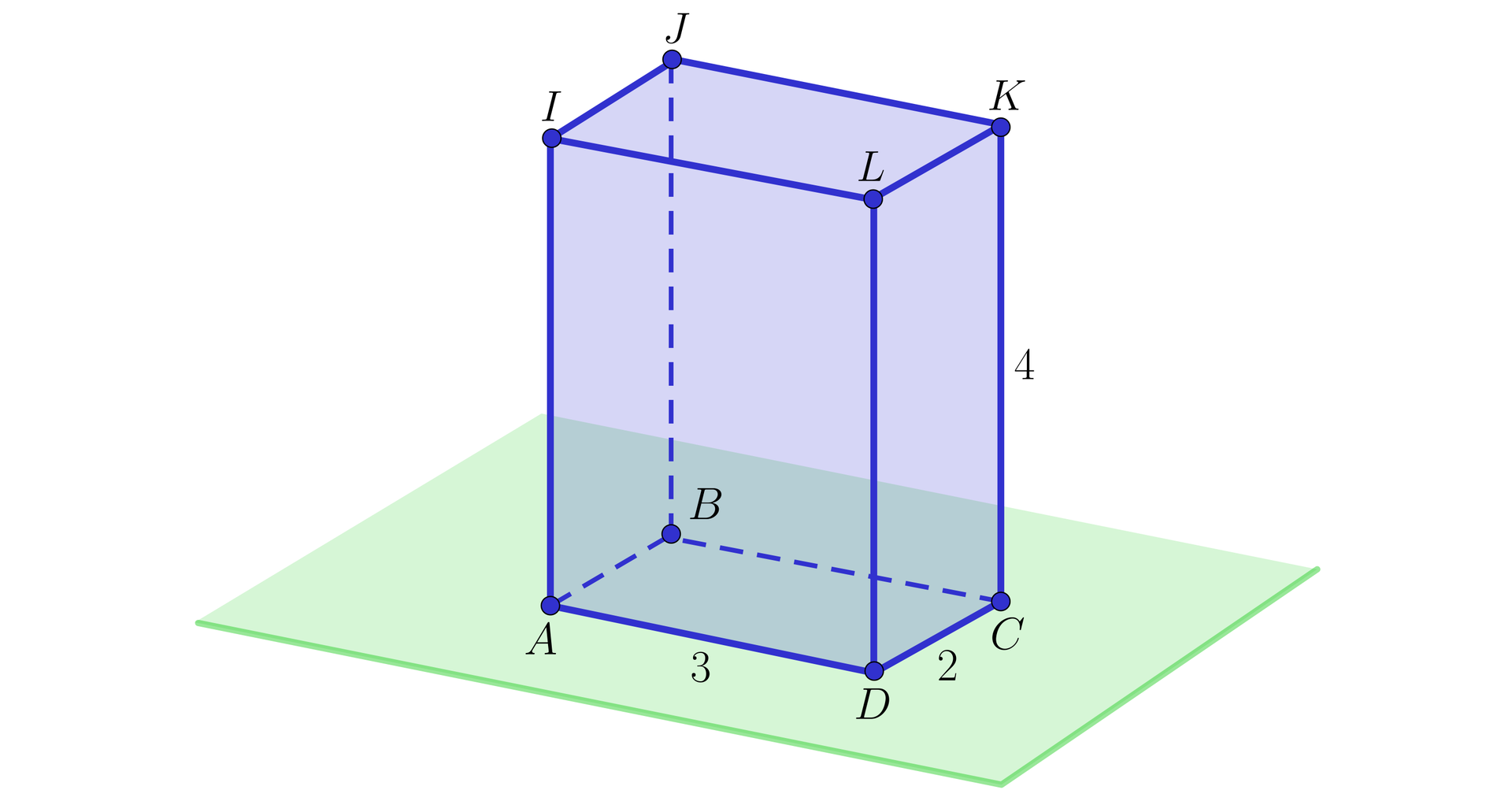
Ilustracja przedstawia prostopadłościan A B C D I J K L, gdzie wierzchołek I znajduje się nad A, wierzchołek J nad B, wierzchołek K nad C, wierzchołek L nad D oraz płaszczyznę zawierającą się w dolnej podstawie A B C D. Podpisano także długości odpowiednich odcinków. Odcinek A D o długości trzy, odcinek D C o długości dwa oraz odcinek C K o długości cztery.

Odległość każdego z punktów $I$ , $J$ , $K$ , $L$ od płaszczyzny $A B C D$ jest równa $4$ . Odległość każdego z punktów $D$ , $C$ , $K$ , $L$ od płaszczyzny $A B J I$ jest równa $3$ . Odległość każdego z punktów $A$ , $D$ , $L$ , $I$ od płaszczyzny $B C K J$ jest równa $2$ .

Przykład 2

Punkty $A$ i $B$ leżą na płaszczyźnie $π$ . Odcinki $A C$ i $B D$ są prostopadłe do tej płaszczyzny i mają odpowiednio długości $10$ i $8$ . Uzasadnimy, że proste $A D$ i $B C$ przecinają się w jednym punkcie oraz obliczymy odległość tego punktu od płaszczyznyodległość punktu od płaszczyznyodległość tego punktu od płaszczyzny $π$ .

Rozwiązanie

Możemy zauważyć, że ponieważ proste $A C$ i $B D$ są prostopadłe do tej samej płaszczyzny, którą jest $π$ , to są one równoległe. Wynika stąd, że leżą na jednej płaszczyźnie – nazwijmy ją $φ$ . Oznacza to, że proste $A D$ i $B C$ też leżą na płaszczyźnie $φ$ , więc przecinają się w jednym punkcie, nazwijmy go $S$ .

Zauważmy teraz, że możliwe są dwa przypadki położenia punktów $A$ i $B$ względem płaszczyzny $π$ :

I. Punkty $C$ i $D$ leżą po tej samej stronie płaszczyzny $π$ .

RtX9RKRZkuPwJ

Ilustracja przedstawia płaszczyznę pi oraz dwa trójkąty prostokątne o tej samej podstawie A B. Pierwszy trójkąt A B C posiada kąt prosty przy wierzchołku A oraz kąt alfa przy wierzchołku C. Odcinek A C ma długość dziesięć i jest prostopadły do płaszczyzny pi. Drugi trójkąt A B D posiada kąt prosty przy wierzchołku B. Odcinek B D ma długość osiem i również jest prostopadły do płaszczyzny pi. Odcinki A C i B D są do siebie równoległe. Odcinki A D i B C przecinają się w punkcie S tworząc trójkąt A B S. Z punktu S poprowadzono wysokość trójkąta upuszczoną na podstawę A B w punkcie S prim. Powstał nowy trójkąt B S S prim, z zaznaczonym kątem prostym przy wierzchołku S prim oraz kątem alfa przy wierzchołku S.

Ponieważ proste $A C$ i $B D$ są równoległe, więc kąty $A C B$ i $C B D$ mają równe miary (kąty naprzemianległe). Również kąty $A C B$ i $S' S B$ mają równe miary (kąty odpowiadające). Na mocy cechy kąt‑kąt‑kąt trójkąt $S S' B$ jest podobny do trójkąta $C A B$ oraz trójkąt $A C S$ jest podobny do trójkąta $D B S$ . Z powyższych podobieństw wynikają stosunki:

$\frac{|S S'|}{|B S|} = \frac{|A C|}{|B C|}$ oraz $\frac{|C S|}{|A C|} = \frac{|B S|}{|B D|}$

czyli

$\frac{|S S'|}{|B S|} = \frac{10}{|C S| + |B S|}$ oraz $\frac{|C S|}{10} = \frac{|B S|}{8}$ .

Z pierwszej równości mamy

$|S S'| = \frac{10 |B S|}{|C S| + |B S|} (*)$

zaś z drugiej

$|C S| = \frac{10 |B S|}{8} = \frac{5 |B S|}{4}$ .

Możemy teraz $|C S| = \frac{5 |B S|}{4}$ podstawić do równości $(*)$ :

$|S S'| = \frac{10 |B S|}{|C S| + |B S|} = \frac{10 |B S|}{\frac{5 |B S|}{4} + |B S|} = \frac{10}{\frac{5}{4} + 1} = \frac{10}{\frac{9}{4}} = \frac{40}{9}$

Zatem odległość punktu $S$ od płaszczyzny $π$ to $\frac{40}{9} = 4 \frac{4}{9}$ .

II. Punkty $C$ i $D$ leżą po różnych stronach płaszczyzny $π$ .

Rh4zDCzPCPjTw

Ilustracja przedstawia płaszczyznę pi. Na płaszczyźnie zaznaczono dwa punkty, punkt A oraz B. Nad punktem A znajduje się punkt C, natomiast długość odcinka A C ma długość dziesięć. Utworzono trójkąt prostokątny A B C o kącie prostym przy wierzchołku A oraz kącie beta przy wierzchołku B. Poniżej punktu B pod płaszczyzną znajduje się punkt D, natomiast odcinek B D ma długość dziesięć. Przedłużono przeciwprostokątną C B trójkąta A B C, oraz przedłużono odcinek A D. Miejsce przecięcia się obu prostych znajdujące się pod płaszczyzną pi oznaczono puntem S. Punkt S zrzutowano na płaszczyznę pi tworząc tym samym punkt S prim oraz trójkąt prostokąty B S S prim. Wewnątrz tego trójkąta zaznaczono kąt prosty znajdujący się przy wierzchołku S prim oraz kąt beta przy wierzchołku B.

W tym przypadku możemy zauważyć, że kąty $A B C$ oraz $S^{'} B S$ mają równe miary jako kąty wierzchołkowe. Zatem na mocy cechy kąt‑kąt‑kąt podobne są trójkąty $A B C$ i $S' B S$ . Jako że kąt $B A D$ jest kątem wspólnym trójkątów prostokątnych $B A D$ i $S' A S$ , to na mocy cechy kąt‑kąt‑kąt trójkąty również są podobne.

Z podobieństw tych wynikają stosunki:

$\frac{|A C|}{|A B|} = \frac{|S S'|}{|B S'|}$ oraz $\frac{|A B|}{|B D|} = \frac{|A S'|}{|S S'|}$ .

Po podstawieniu otrzymujemy odpowiednio

$\frac{10}{|A B|} = \frac{|S S'|}{|B S'|}$ oraz $\frac{|A B|}{8} = \frac{|A B| + |B S'|}{|S S'|}$ .

Z pierwszego równania mamy $|B S'| = \frac{|A B| \cdot |S S'|}{10}$ , co możemy podstawić do drugiego równania:

$\frac{|A B|}{8} = \frac{|A B| + \frac{|A B| \cdot |S S'|}{10}}{|S S'|}$ , które po przekształceniach daje kolejno

$|A B| \cdot |S S'| = 8 |A B| + \frac{8}{10} |A B| \cdot |S S'|$

$|S S'| = 8 + \frac{4}{5} |S S'|$

$\frac{1}{5} |S S'| = 8$

$|S S'| = 40$

Zatem odległość punktu przecięcia prostych $A D$ i $B C$ od płaszczyzny $π$ w tym przypadku jest równa $40$ .

Uwaga!

W rozwiązaniu powyższego zadania można posłużyć się znanym faktem z geometrii płaszczyzny. Jeśli poprowadzimy prostą równoległą do podstaw $|A B| = a$ i $|C D| = b$ trapezu $A B C D$ , która przechodzi przez punkt $S$ przecięcia przekątnych tego trapezu i przecina ramiona $A D$ i $B C$ w punktach $K$ i $L$ , to każdy z odcinków $K S$ i $L S$ ma długość $\frac{a b}{a + b}$ .

Przykład 3

Zauważmy, że zbiór wszystkich punktów przestrzeni trójwymiarowej, których trzecia współrzędna jest równa $0$ , czyli punktów o współrzędnych $(x, y, 0)$ , tworzy płaszczyznę:

RRyr3kVTzoGWM

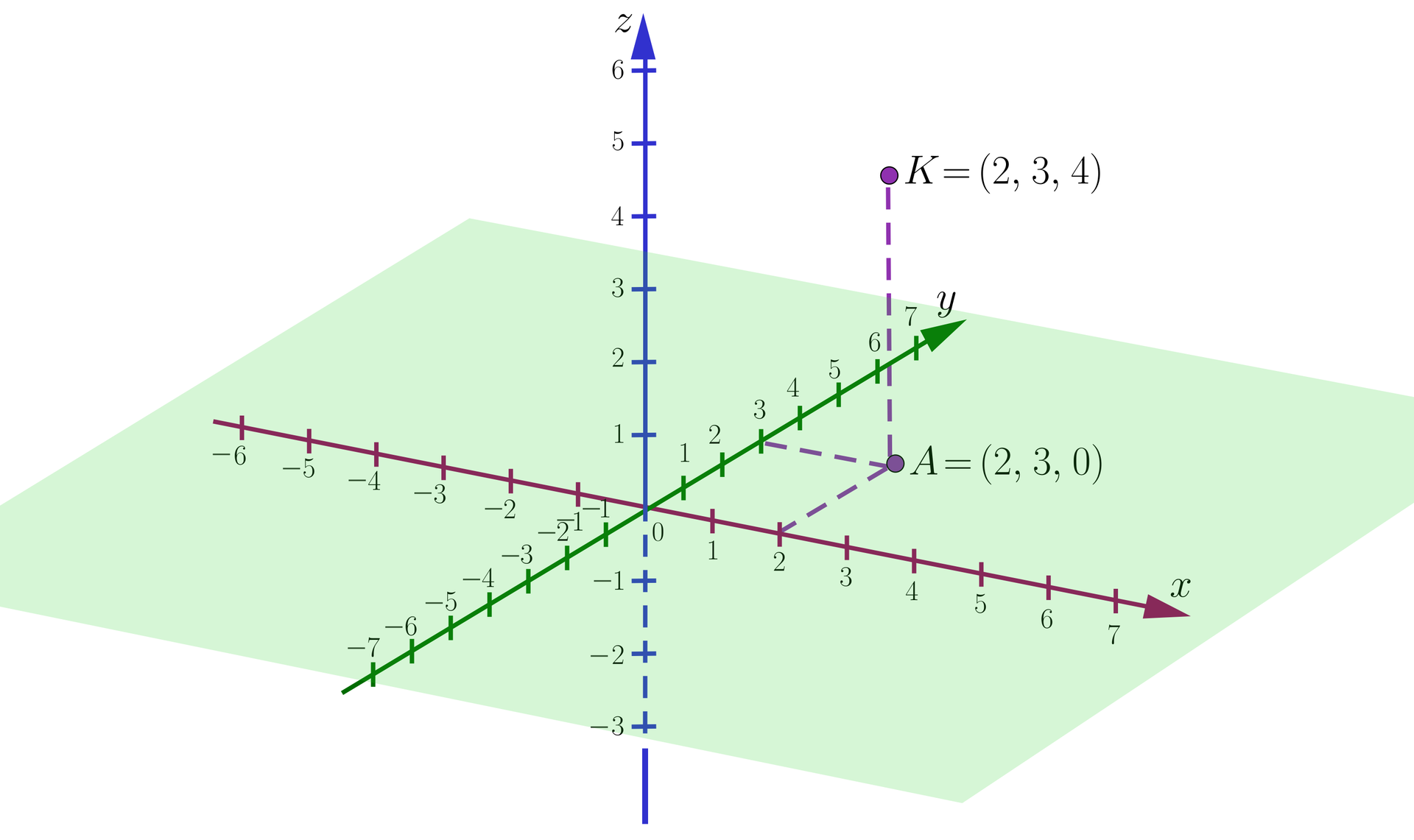
Ilustracja przedstawia trójwymiarowy układ współrzędnych z osią X od minus siedmiu do siedmiu, z osią Y od minus siedmiu do siedmiu oraz z osią Z od minus trzech do sześciu oraz płaszczyznę pi zawierającą się w osiach X i Y. Na układzie współrzędnych zaznaczono również dwa punkty, punkt A zawierający się wewnątrz płaszczyzny pi, o współrzędnych nawias dwa średnik trzy średnik zero koniec nawiasu oraz punkt K znajdujący się nad punktem A, o współrzędnych nawias dwa średnik trzy średnik cztery koniec nawiasu.

Zatem płaszczyzna na rysunku powyżej ma równanie $z = 0$ .

Odległość punktu $K = (2, 3, 4)$ od płaszczyzny o równaniu $z = 0$ jest równa $4$ .

Słownik

odległość punktu od płaszczyzny

jeśli dany punkt leży na płaszczyźnie $π$ , to jego odległość od $π$ jest równa $0$ , jeśli punkt nie leży na płaszczyźnie $π$ , to jego odległość od $π$ jest równa odległości od jego rzutu prostokątnego na $π$

Wprowadzenie

Prezentacja multimedialna

Słownik