Ocenimy, czy  siatka graniastosłupa prawidłowego czworokątnegograniastosłup prawidłowy czworokątnygraniastosłupa prawidłowego czworokątnego może zawierać:

a) $4$ kwadraty o boku $a$ oraz $2$ prostokąty o bokach $a$ i $b$

Rozwiązanie:
Zauważmy, że wybierając dwa kwadraty o boku $a$ na górną i dolną podstawę graniastosłupa prawidłowego czworokątnego, dwa pozostałe kwadraty oraz $2$ prostokąty o bokach $a$ i $b$ będą tworzyć jego powierzchnię boczną. Nie są to figury przystające, więc z podanych wielokątów nie możemy zbudować siatki graniastosłupa prawidłowego czworokątnego.

b) dokładnie $5$ kwadratów o boku $a$

Rozwiązanie:
Siatka dowolnego graniastosłupa czworokątnego składa się z sześciu elementów. Zatem nie da się zbudować z podanych elementów graniastosłupa prawidłowego czworokątnego.

Obliczymy pole powierzchni całkowitej graniastosłupówpole powierzchni całkowitej graniastosłupa prawidłowego czworokątnegopole powierzchni całkowitej graniastosłupów których siatki przedstawiają poniższe rysunki.

Rozwiązanie:

a) Rysunek przedstawia siatkę sześcianu.

R15Kb5pD6ZuTn

Grafika przedstawia siatkę sześcianu. Siatka przedstawiona jest w taki sposób że cztery kwadraty o boku a ułożone są jeden na drugim a do drugiego od góry kwadratu przylegają kwadraty po obu stronach tworząc krzyż. W kwadracie na samym dole oznaczono boki odległością a oraz przekątną tego kwadratu o długości 4.

Ze wzoru na przekątną kwadratu (ściany sześcianu) mamy $a\sqrt{2}=4$.

Stąd wyliczamy długość krawędzi sześcianu $a=2\sqrt{2}$. Zatem pole powierzchni $P_c=6a^2=6·8=48$.

b) Rysunek przedstawia siatkę graniastosłupa prawidłowego czworokątnego.

Ra1EiiG2mfqTS

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego o podstawie kwadratu o boku a i wysokości h. Siatka przedstawiona jest w taki sposób że cztery prostokąty o podstawie a i wysokości h ułożone są przylegająco wysokościami . Powyżej oraz poniżej do drugiego prostokąta przylegają kwadraty o boku a. W trzecim prostokącie oznaczono kąt $60°$ między przekątną o długości 4 a podstawą a. W pierwszym prostokącie oznaczono kąt prosty między podstawą a i wysokością h.

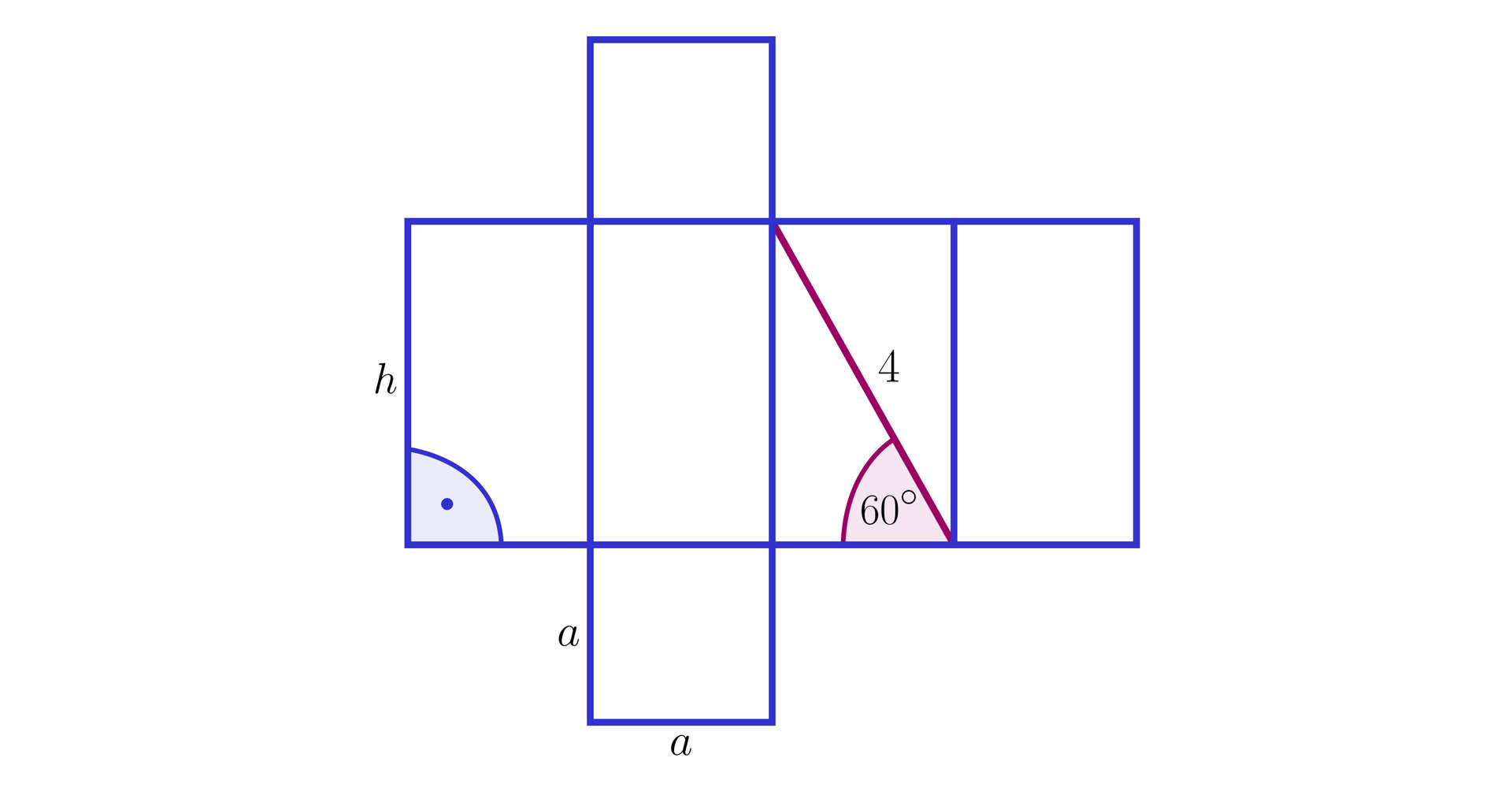
Aby obliczyć pole powierzchni całkowitej znajdziemy długość krawędzi podstawy oraz długość wysokości.

Przekątna ściany bocznej ma długość $4$ i jest nachylona do krawędzi podstawy pod kątem o mierze $60°$. Mamy zatem $\sin 60°=\frac{h}{4}=\frac{\sqrt{3}}{2}$, stąd $h=2\sqrt{3}$.

Obliczymy długość krawędzi podstawy. Mamy $\cos 60°=\frac{a}{4}=\frac{1}{2}$, stąd $a=2$.

Możemy obliczyć pole powierzchni całkowitej:

$P_c=2a^2+4ah=2·2^2+4·2\sqrt{3}·2=8+16\sqrt{3}$.

Obliczymy pole powierzchnipole powierzchni całkowitej graniastosłupa prawidłowego czworokątnegopole powierzchni i objętość graniastosłupa prawidłowego czworokątnegoobjętość graniastosłupa prawidłowego czworokątnegoobjętość graniastosłupa prawidłowego czworokątnego, którego siatkę przedstawia poniższy rysunek.

R9ueVUQ7MNWGT

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego o podstawie kwadratu o boku a i wysokości h. Siatka przedstawiona jest w taki sposób że cztery prostokąty o podstawie a i wysokości h ułożone są przylegająco wysokościami . W ostatnim prostokącie oznaczono przekątne przecinające się pod kątem $\alpha$ równym $60°$ . Podstawa prostokątna ma długość $4\sqrt{3}$. Powyżej oraz poniżej do drugiego prostokąta przylegają kwadraty.

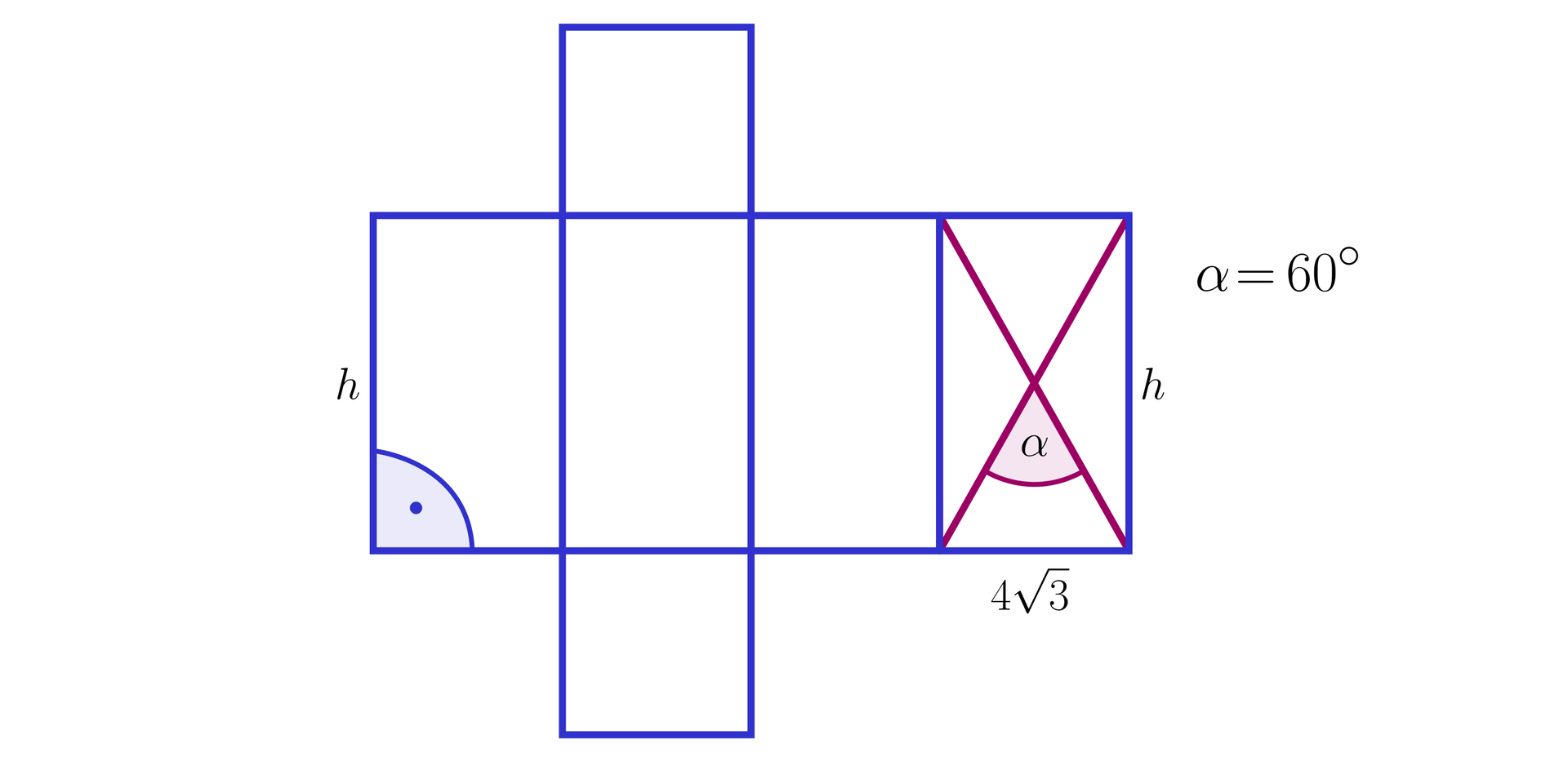
Rozwiązanie:

R15SHHQnJebm6

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego o podstawie kwadratu o boku a i wysokości h. Siatka przedstawiona jest w taki sposób że cztery prostokąty o podstawie a i wysokości h ułożone są przylegająco wysokościami . W ostatnim prostokącie oznaczono przekątne przecinające się pod kątem równym $60°$ . Podstawa prostokątna ma długość $4\sqrt{3}$. Powyżej oraz poniżej do drugiego prostokąta przylegają kwadraty. Ostatni prostokąt oznaczono jako ABCD z punktem przecięcia się przekątnych S.

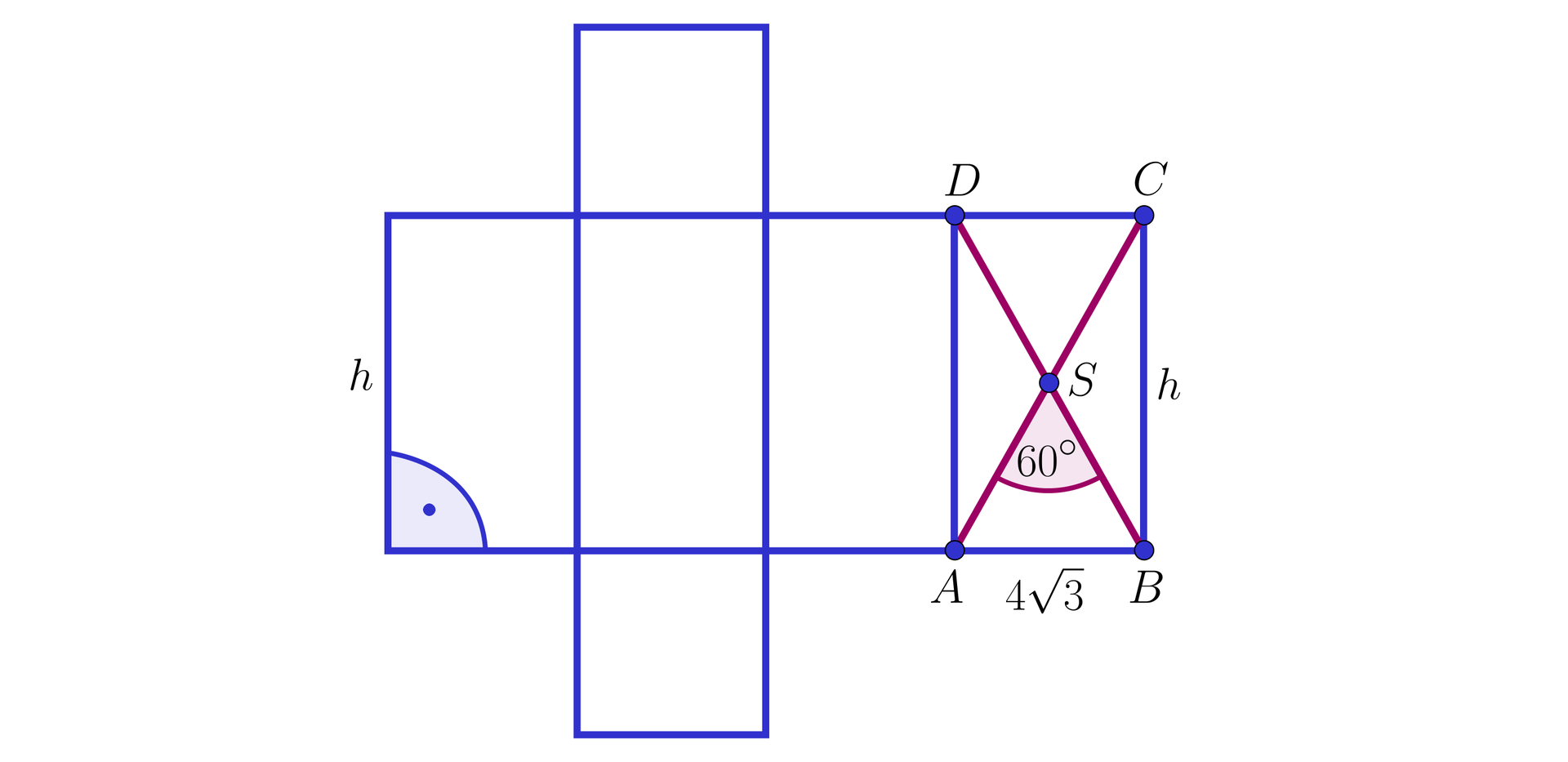
Rozważmy siatkę graniastosłupa prawidłowego czworokątnego przedstawionego na rysunku powyżej. Przekątne ściany bocznej, która jest prostokątem, przecinają się pod kątem ostrym o mierze $60°$.

Trójkąt $ABS$ jest trójkątem równoramiennym (w prostokącie przekątne są równe i dzielą się na połowy), zatem kąty $\sphericalangle SAB$ oraz $\sphericalangle SBA$ mają równe miary, po $60°$.

Stąd trójkąt $ASB$ jest nie tylko równoramienny, ale i równoboczny.

Zatem $\left|AS\right|=\left|BS\right|=\left|AB\right|=4\sqrt{3}$.

Przekątne ściany bocznej, która jest prostokątem dzielą się na połowy, czyli $\left|BS\right|=\left|SD\right|=4\sqrt{3}$, stąd $\left|BD\right|=8\sqrt{3}$.

Korzystając z twierdzenia Pitagorasatwierdzenie Pitagorasatwierdzenia Pitagorasa dla trójkąta $ABD$ możemy wyliczyć długość boku $h$, który jest również wysokością graniastosłupa:

$h^2={\left(8\sqrt{3}\right)}^2-{\left(4\sqrt{3}\right)}^2=144$, zatem $h=12$.

Możemy policzyć pole powierzchni całkowitej i objętość graniastosłupaobjętość graniastosłupa prawidłowego czworokątnegoobjętość graniastosłupa:

$P_c=2·{\left(4\sqrt{3}\right)}^2+4·12·4\sqrt{3}=96+192\sqrt{3}$,

$V={\left(4\sqrt{3}\right)}^2·12=576$.

Korzystając z danych przedstawionych na siatce graniastosłupa prawidłowego czworokątnego obliczymy jego pole powierzchni.

Ro6krSE6kOdqM

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego o podstawie kwadratu. Siatka przedstawiona jest w taki sposób że cztery prostokąty ułożone są przylegająco dłuższymi bokami czyli wysokościami h. Powyżej pierwszego prostokąta oraz poniżej ostatniego przylegają kwadraty o boku a. W drugim prostokącie oznaczono kąt prosty pomiędzy wysokością a podstawą prostokąta. W pierwszym prostokącie na środka dłuższych boków leżą punkty P i R. Od tych punktów odchodzą odcinki do punktu S leżącego na środku podstawy oznaczonej AB . Odcinki te mają długość 3 a kąt pomiędzy nimi wynosi $60°$. Odcinki PA oraz RB mają długość równą $\frac{1}{2}h$ a odcinek AS ma długość $\frac{1}{2}a$.

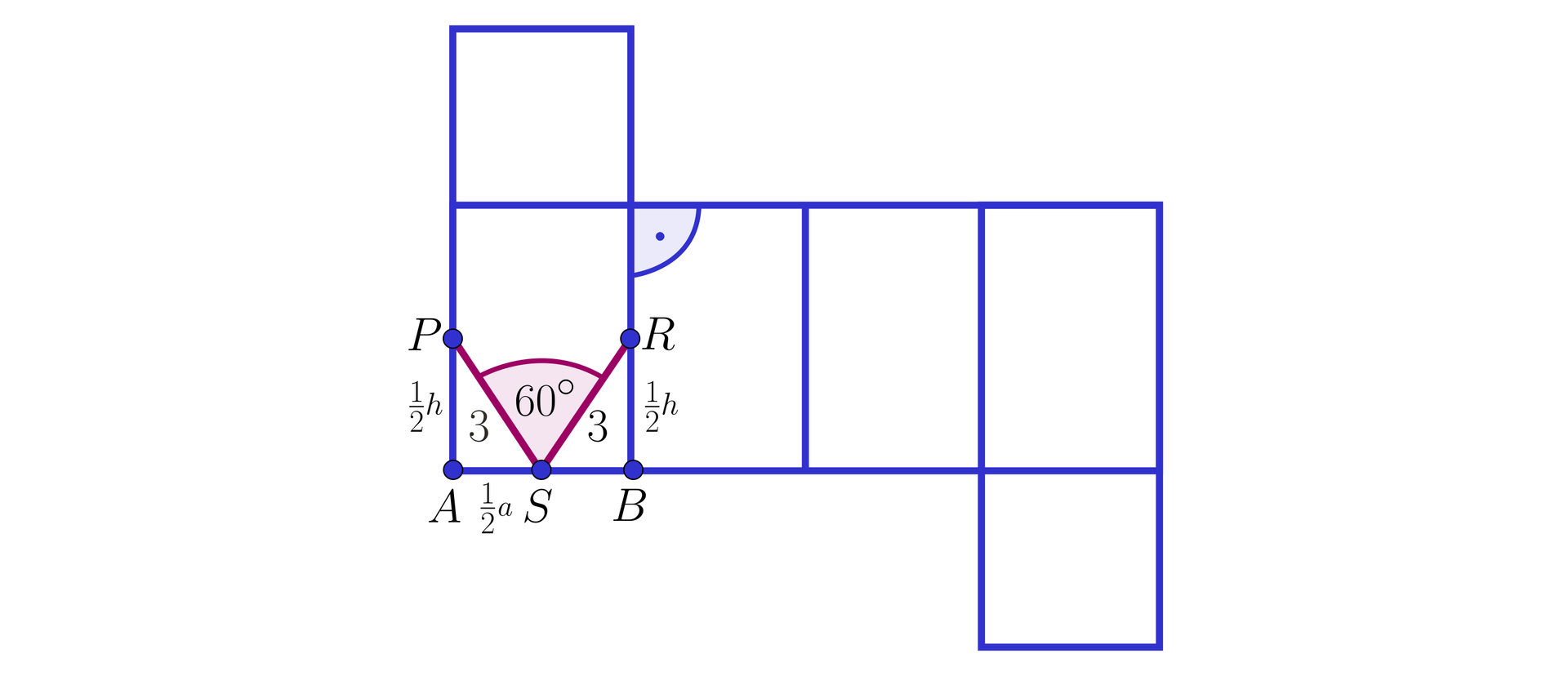
Rozwiązanie:

Z przedstawionego rysunku mamy:

$\left|PS\right|=\left|SR\right|=3$ oraz kąty $\sphericalangle PSA$ i $\sphericalangle RSB$ są równe, bo trójkąty $PAS$ i $RBS$ są prostokątne i przystające.

Zatem $\sphericalangle PSA=\sphericalangle RSB=60°$.

Dla trójkąta $PAS$ mamy $\mathrm{tg}60°=\frac{\frac{1}{2}h}{\frac{1}{2}a}=\sqrt{3}$, stąd $h=a\sqrt{3}$.

Korzystając z twierdzenia Pitagorasa dla trójkąta $PAS$ mamy:

$\frac{1}{4}{h}^2+\frac{1}{4}{a}^2=9$.

Podstawiając za $h=a\sqrt{3}$ otrzymujemy $\frac{3}{4}{a}^2+\frac{1}{4}{a}^2=9$, stąd $a^2=9$, czyli $a=3$ i $h=3\sqrt{3}$.

Możemy policzyć pole powierzchni całkowitej graniastosłupa:

$P_c=2·3^2+4·3·3\sqrt{3}=18+36\sqrt{3}$.

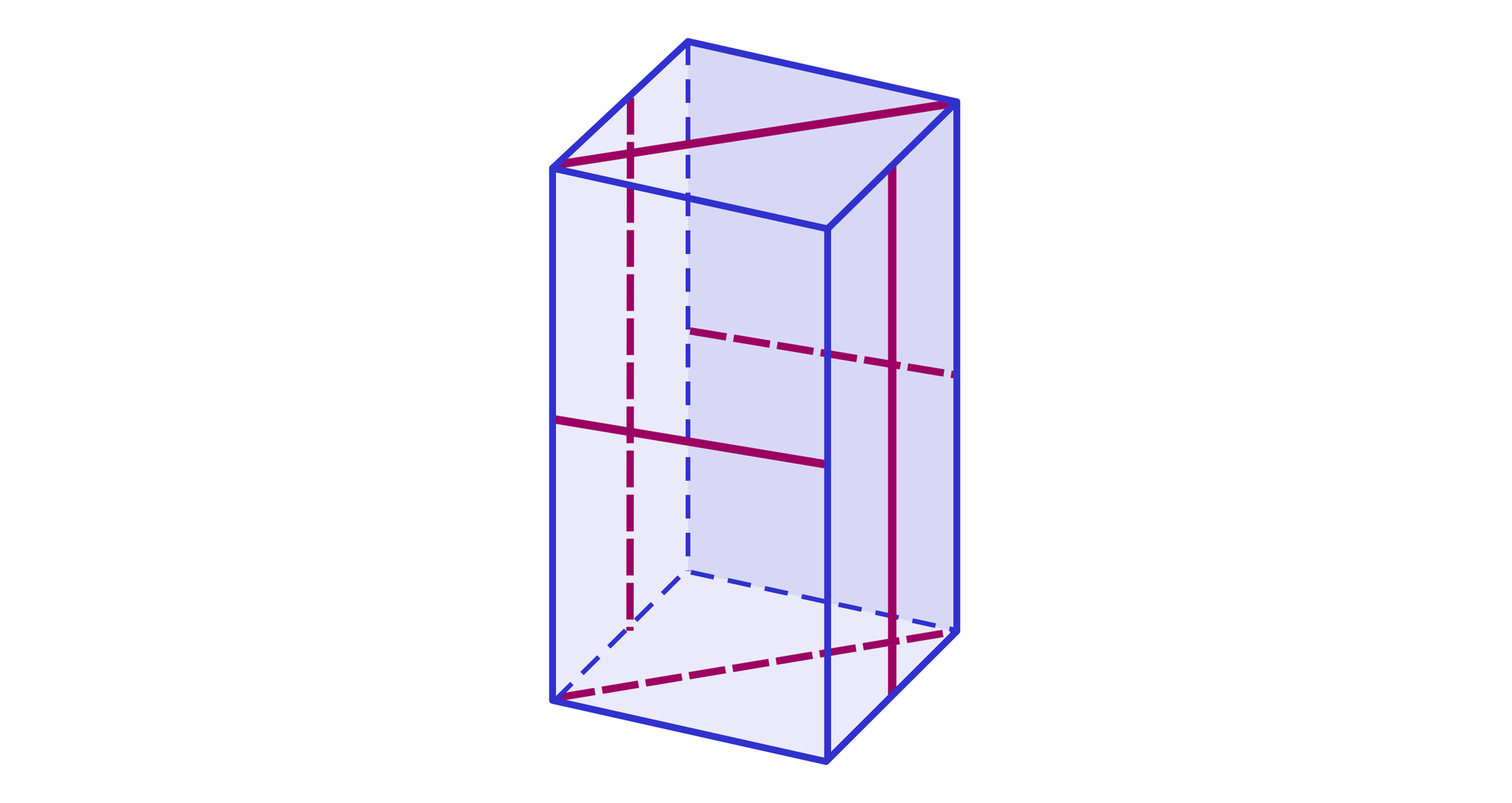
Który z poniższych rysunków przedstawia siatkę z której można skleić graniastosłup prawidłowy czworokątnygraniastosłup prawidłowy czworokątnygraniastosłup prawidłowy czworokątny przedstawiony na poniższym rysunku.

RV0YHisgQsE67

Grafika przedstawia graniastosłup prawidłowy czworokątny. Przekątne podstaw oznaczone są czerwonymi liniami , jedna przerywaną a druga ciągłą. Boki graniastosłupa również podzielono na pół liniami , dwa wzdłużnie a dwa poprzecznie, naprzemianlegle. Jeden poprzecznie podzielono linią przerywaną a drugi ciągłą. Wzdłużnie boki podzielono w ten sam sposób.

Rozwiązanie:

a)

R13D6afSazJmI

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego. Siatka przedstawiona jest w taki sposób że cztery prostokąty ułożone są przylegająco wysokościami. Powyżej oraz poniżej drugiego prostokąta przylegają kwadraty. Przekątne kwadratów oznaczone są czerwonymi liniami. Boki graniastosłupa również podzielono na pół liniami , dwa wzdłużnie a dwa poprzecznie na mniejsze prostokąty, naprzemianlegle tak że pierwszy i trzeci prostokąt podzielone są na węższe prostokąty a drugi i czwarty na kwadraty.

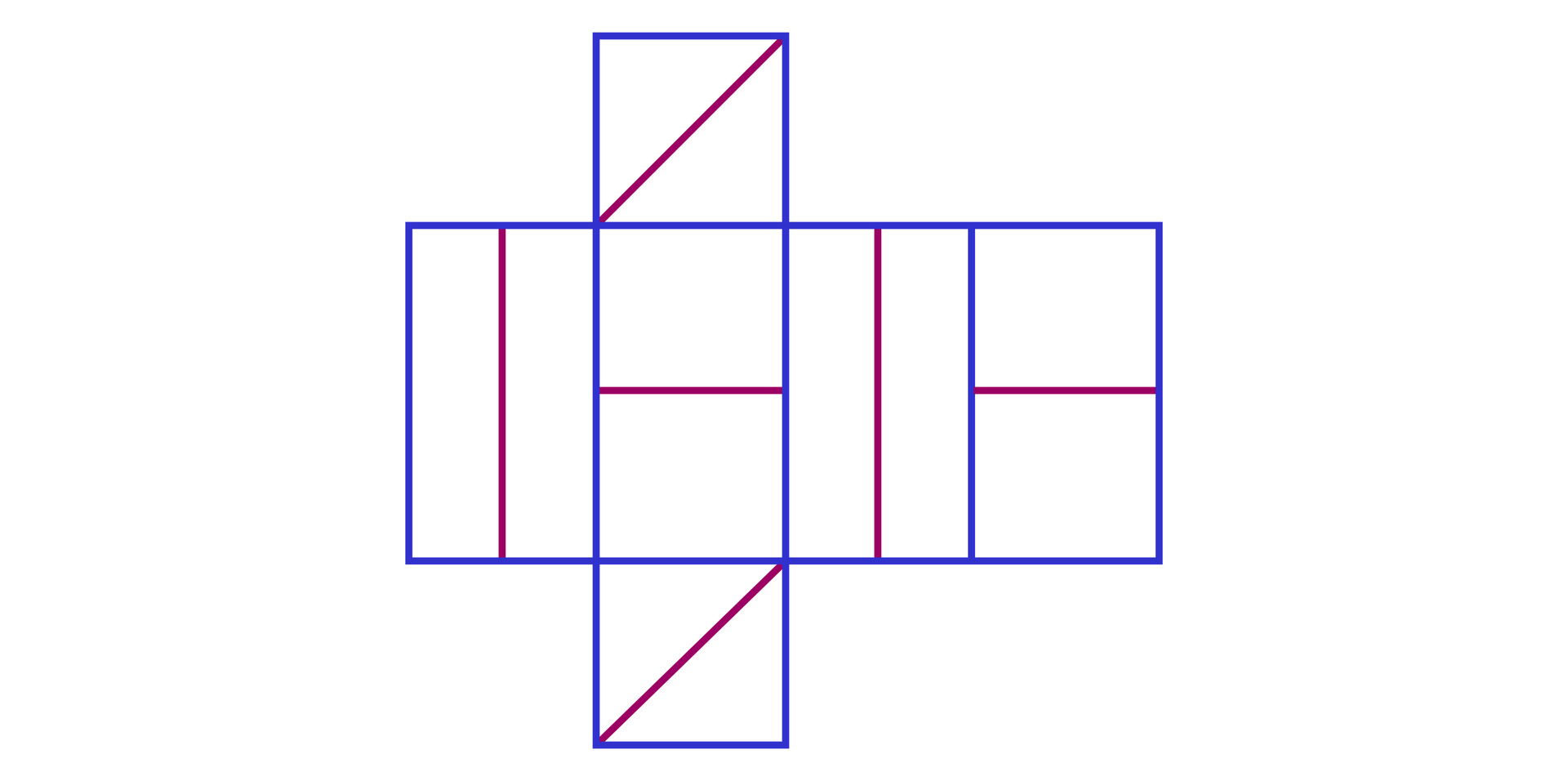
Rysunek przedstawia prawidłową siatkę. Odcinki na przeciwległych ścianach bocznych i podstawach są równoległe do siebie.

b)

R9Z92VXHK2XX7

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego. Siatka przedstawiona jest w taki sposób że cztery prostokąty ułożone są przylegająco wysokościami. Powyżej oraz poniżej do drugiego prostokąta przylegają kwadraty. Przekątne kwadratów oznaczone są czerwonymi liniami. Boki graniastosłupa również podzielono na pół liniami , dwa wzdłużnie a dwa poprzecznie na mniejsze prostokąty, naprzemianlegle tak że pierwszy i czwarty prostokąt podzielone są na węższe prostokąty a drugi i trzeci na kwadraty.

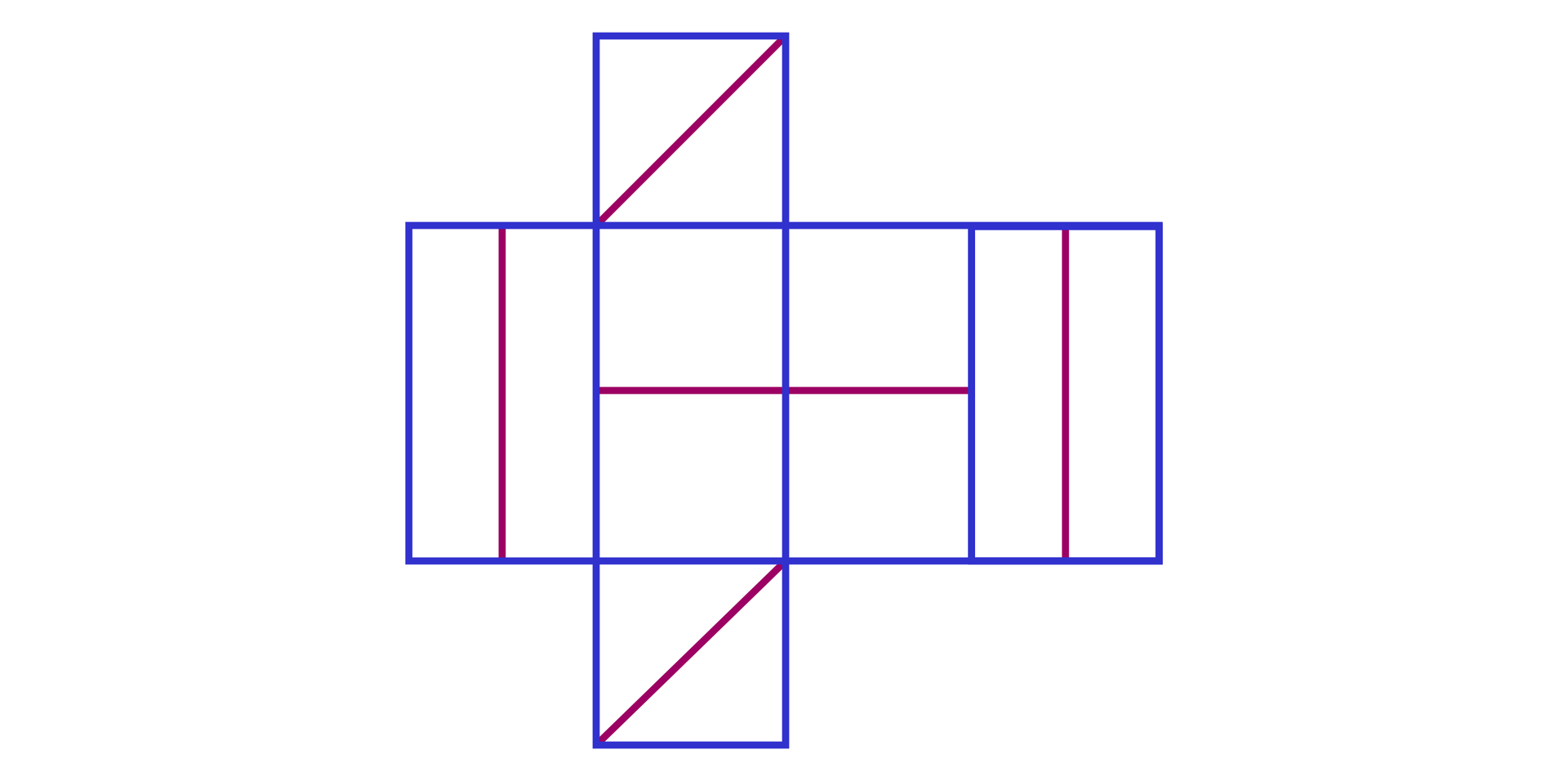
Rysunek nie przedstawia prawidłowej siatki. Odcinki na przeciwległych ścianach bocznych nie są równoległe do siebie.

c)

Rd554pvHBXm1C

Grafika przedstawia siatkę graniastosłupa prawidłowego czworokątnego. Siatka przedstawiona jest w taki sposób że cztery prostokąty ułożone są przylegająco wysokościami. Powyżej oraz poniżej do drugiego prostokąta przylegają kwadraty. Kwadraty podstaw przedzielono w połowie czerwonymi liniami tworząc prostokąty. Boki graniastosłupa również podzielono na pół liniami , dwa wzdłużnie a dwa poprzecznie na mniejsze prostokąty, naprzemianlegle tak że pierwszy i trzeci prostokąt podzielone są na węższe prostokąty a drugi i czwarty na kwadraty.

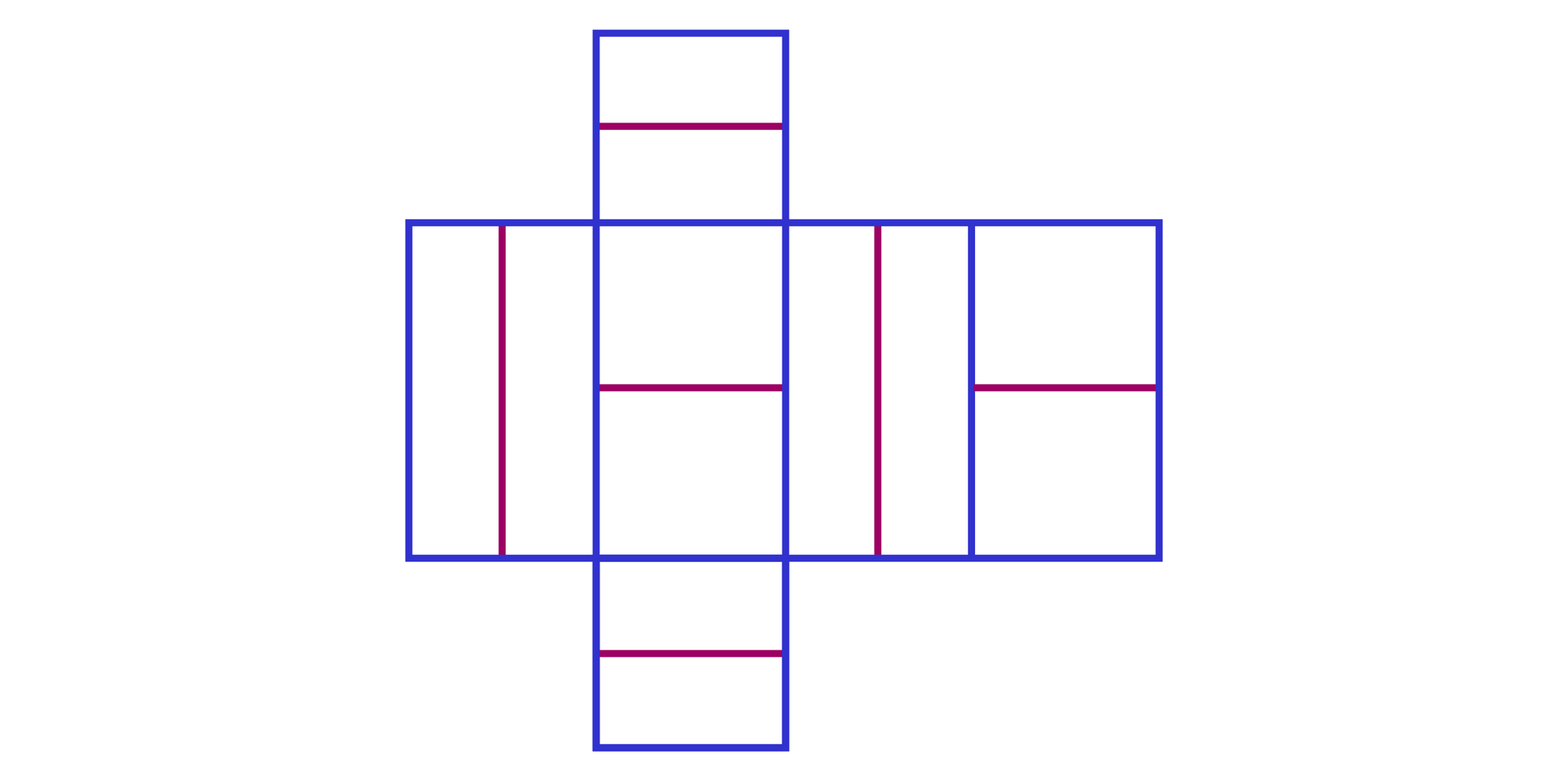
Rysunek nie przedstawia prawidłowej siatki. Odcinki na przeciwległych ścianach bocznych są równoległe do siebie, ale odcinki na podstawach nie są równoległymi przekątnymi podstaw.

jest to graniastosłup prosty, którego podstawą jest kwadrat

w dowolnym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej tego trójkąta

jest równa iloczynowi pola podstawy przez wysokość

jest równe sumie pól jego podstaw i pola powierzchni bocznej; pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe polu jego siatki