Przeczytaj

Równanie kwadratowe zupełne – jest to równanie postaci:

a x^{2} + b x + c = 0,

gdzie:
$a$ , $b$ i $c$ – są dowolnymi liczbami rzeczywistymi różnymi od zera.

Liczba rozwiązań równania kwadratowego zupełnego jest uzależniona od znaku wyróżnika trójmianu kwadratowego, zwanego deltą.

Liczba rozwiązań równania kwadratowego

Twierdzenie: Liczba rozwiązań równania kwadratowego

Rozważmy równanie kwadratowe $a x^{2} + b x + c = 0$ , $a \neq 0$ .

Jeżeli $∆ > 0$ , to równanie ma dwa pierwiastki:
$x_{1} = \frac{- b - \sqrt{∆}}{2 a}$ , $x_{2} = \frac{- b + \sqrt{∆}}{2 a}$ .
Jeżeli $∆ = 0$ , to równanie ma jeden pierwiastek, nazwany podwójnym pierwiastkiem:
$x_{0} = \frac{- b}{2 a}$ .
Jeżeli $∆ < 0$ , to równanie nie ma pierwiastków.

Dlatego w rozwiązywaniu zadań dotyczących analizy liczby rozwiązań równania rozpatrujemy znak wyróżnika trójmianu kwadratowego.

Aby pierwiastki równania kwadratowego zupełnegorównanie kwadratowe zupełnerównania kwadratowego zupełnego były określonego znaku, dodajemy jeszcze warunki związane ze wzorami Viete’a.

Równanie kwadratowe ma dwa pierwiastki jednakowych znaków wtedy i tylko wtedy, gdy spełnione są następujące warunki:

$\{\begin{cases} 1 . ∆ \geq 0 \\ 2 . x_{1} \cdot x_{2} > 0 \end{cases}$ .

Równanie kwadratowe ma dwa pierwiastki różnych znaków wtedy i tylko wtedy, gdy spełnione są następujące warunki:

$\{\begin{cases} 1 . ∆ > 0 \\ 2 . x_{1} \cdot x_{2} < 0 \end{cases}$ .

Równanie kwadratowe ma dwa różne pierwiastki ujemne wtedy i tylko wtedy, gdy spełnione są warunki:

$\{\begin{cases} 2 . ∆ > 0 \\ 3 . x_{1} \cdot x_{2} > 0 \\ 4 . x_{1} + x_{2} < 0 \end{cases}$ .

Równanie kwadratowe ma dwa różne pierwiastki dodatnie wtedy i tylko wtedy gdy, spełnione są warunki:

$\{\begin{cases} 2 . ∆ > 0 \\ 3 . x_{1} \cdot x_{2} > 0 \\ 4 . x_{1} + x_{2} > 0 \end{cases}$ .

Przykład 1

Wyznaczymy takie wartości parametru $m$ , dla których równanie kwadratowe $(m - 2) x^{2} + 2 m x + (m + 3) = 0$ ma dwa różne pierwiastki rzeczywiste.

Rozwiązanie

Najpierw ustalimy, dla jakich wartości parametru $m$ równanie jest kwadratowe.

Aby równanie było kwadratowe: $m - 2 \neq 0 \Rightarrow m \neq 2$ .

Aby równanie miało dwa różne pierwiastki rzeczywiste $∆ > 0$ .

Wyznaczymy wyrównik trójmianu:

$∆ = {(2 m)}^{2} - 4 \cdot (m - 2) (m + 3) = 4 m^{2} - 4 \cdot (m^{2} + 3 m - 2 m - 6) =$

Zatem:

$= 4 m^{2} - 4 m^{2} - 4 m + 24 = - 4 m + 24$

$- 4 m + 24 > 0$

$- 4 m > - 24$

$m < 6$

Czyli $\{\begin{cases} m \in ℝ ∖ \{2\} \\ m \in (- \infty, 6) \end{cases}$ .

Zatem, aby równanie miało dwa różne pierwiastki rzeczywiste, musi zachodzić warunek $m \in (- \infty, 2) \cup (2, 6)$ .

Przykład 2

Ustalimy liczbę pierwiastków równania $z x^{2} - 4 x - 1 = 0$ w zależności od parametru $z$ .

Rozwiązanie

1. Jeżeli $z = 0$ równanie jest liniowe. Obliczymy teraz rozwiązanie tego równania.
$0 \cdot x^{2} - 4 x - 1 = 0$
$- 4 x = 1$
$x = - \frac{1}{4}$
Czyli dla $z = 0$ równanie liniowe ma jedno rozwiązanie.

2. Jeżeli $z \in ℝ ∖ \{0\}$ równanie jest kwadratowe.
$z x^{2} - 4 x - 1 = 0$
$∆ = {(- 4)}^{2} - 4 \cdot z \cdot (- 1) = 16 + 4 z$ .

Aby równanie kwadratowe miało dwa rozwiązania $∆ > 0$ .
$16 + 4 z > 0$
$4 z > - 16$
$z > - 4$
$z \in (- 4, 0) \cup (0, \infty)$ .
Aby równanie kwadratowe miało jedno rozwiązanie $∆ = 0$ , czyli $z = - 4$ .
Aby równanie kwadratowe nie posiadało rozwiązań $∆ < 0$ , czyli $z < - 4$ .
$z \in (- \infty, - 4)$ .

Odpowiedź:

Równanie $z x^{2} - 4 x - 1 = 0$ ma:

dwa rozwiązania dla $z \in (- 4, 0) \cup (0, \infty)$ ,

jedno rozwiązanie dla $z \in \{- 4, 0\}$ ,

nie posiada rozwiązań dla $z \in (- \infty, - 4)$ .

Przykład 3

Obliczymy, dla jakich wartości parametru $m$ równanie $(m + 3) x^{2} + 2 x + (m - 2) = 0$ ma dokładnie jedno rozwiązanie.

Rozwiązanie

Dla $m + 3 = 0$ , czyli $m = - 3$ , równanie jest liniowe.
$2 x + (- 3 - 2) = 0$
$2 x - 5 = 0$
$2 x = 5$
$x = \frac{5}{2}$
Równanie ma dokładnie jedno rozwiązanie.
Jeżeli $m \neq - 3$ , to otrzymujemy równanie kwadratowe, które ma jedno rozwiązanie, jeżeli $∆ = 0$ .
$(m + 3) x^{2} + 2 x + (m - 2) = 0$
$∆ = 4 - 4 \cdot (m + 3) (m - 2) = 4 - 4 \cdot (m^{2} - 2 m + 3 m - 6) =$
$= 4 - 4 m^{2} - 4 m + 24 = - 4 m^{2} - 4 m + 28$
$∆ = 0$ wtedy i tylko wtedy, gdy: $- 4 m^{2} - 4 m + 28 = 0 | : (- 4)$
$m^{2} + m - 7 = 0$
$∆_{m} = 1 - 4 \cdot (- 7) = 29 \Rightarrow \sqrt{∆_{m}} = \sqrt{29}$
$m_{1} = \frac{- 1 - \sqrt{29}}{2}$
$m_{2} = \frac{- 1 + \sqrt{29}}{2}$
Równanie ma jedno rozwiązanie dla $m \in \{- 3, \frac{- 1 - \sqrt{29}}{2}, \frac{- 1 + \sqrt{29}}{2}\}$ .

Przykład 4

Wyznaczymy takie wartości parametru $m$ , dla których suma odwrotności dwóch pierwiastków równania $m x^{2} + (m - 1) x + 3 = 0$ jest równa $1$ .

Rozwiązanie

Równanie musi spełniać warunki:

1. $a \neq 0$

2. $∆ \geq 0$

3. $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 1$

$a \neq 0$ wtedy i tylko wtedy, gdy $m \neq 0$
$∆ = {(m - 1)}^{2} - 4 \cdot m \cdot 3 = m^{2} - 2 m + 1 - 12 m = m^{2} - 14 m + 1$
$m^{2} - 14 m + 1 \geq 0$
$∆_{m} = {(- 14)}^{2} - 4 \cdot 1 = 196 - 4 = 192$
$\sqrt{∆_{m}} = 8 \sqrt{3}$
$m_{1} = \frac{14 - 8 \sqrt{3}}{2} = 7 - 4 \sqrt{3}$
$m_{2} = \frac{14 + 8 \sqrt{3}}{2} = 7 + 4 \sqrt{3}$
$m \in (- \infty, 7 - 4 \sqrt{3}⟩ \cup ⟨7 + 4 \sqrt{3}, \infty)$ .
$\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{x_{2} + x_{1}}{x_{1} \cdot x_{2}} = \frac{\frac{- b}{a}}{\frac{c}{a}} = - \frac{b}{c}$
$\frac{- (m - 1)}{3} = 1$
$m - 1 = - 3$
$m = - 2$ .

Uwzględniając rozwiązane warunków $(1)$ , $(2)$ i $(3)$ otrzymujemy: dla $m = - 2$ suma odwrotności pierwiastków równania jest równa $1$ .

Przykład 5

Wyznaczymy wartości parametru $p$ , dla których równanie $(1 - p) x^{2} - 2 p x + p + 3 = 0$ ma dwa różne pierwiastki ujemne.

Rozwiązanie

Równanie ma dwa różne pierwiastki ujemne wtedy i tylko wtedy, gdy spełnione są warunki:

$\{\begin{cases} 1 . a \neq 0 \\ 2 . ∆ > 0 \\ {3 . x}_{1} \cdot x_{2} > 0 \\ 4 . x_{1} + x_{2} < 0 \end{cases}$ .

$a = 1 - p$
$1 - p \neq 0$
$p \neq 1$ .
$∆ = {(- 2 p)}^{2} - 4 \cdot (1 - p) (p + 3) = 4 p^{2} - 4 \cdot (p + 3 - p^{2} - 3 p) =$
$= 4 p^{2} + 8 p - 12 + 4 p^{2} = 8 p^{2} + 8 p - 12$
$∆ > 0$ wtedy i tylko wtedy, gdy: $8 p^{2} + 8 p - 12 > 0$
$2 p^{2} + 2 p - 3 > 0$
$∆_{p} = 4 - 4 \cdot 2 \cdot (- 3) = 4 + 24 = 28$
$\sqrt{∆_{p}} = \sqrt{28} = 2 \sqrt{7}$
$p_{1} = \frac{- 2 - 2 \sqrt{7}}{4} = \frac{- 1 - \sqrt{7}}{2}$
$p_{2} = \frac{- 2 + 2 \sqrt{7}}{4} = \frac{- 1 + \sqrt{7}}{2}$
$p \in (- \infty, \frac{- 1 - \sqrt{7}}{2}) \cup (\frac{- 1 + \sqrt{7}}{2}, \infty)$ .
$x_{1} \cdot x_{2} > 0$
$\frac{p + 3}{1 - p} > 0 | \cdot {(1 - p)}^{2}$ , $p \neq 1$
$(p + 3) (1 - p) > 0$
$p = - 3 \lor p = 1$
$p \in (- 3, 1)$ .
$x_{1} + x_{2} < 0$
$\frac{2 p}{1 - p} < 0 | \cdot {(1 - p)}^{2}$
$2 p (1 - p) < 0$
$p = 0$ lub $p = 1$
$p \in (- \infty, 0) \cup (1, \infty)$ .

Znajdujemy część wspólną zbioru rozwiązań $(1)$ , $(2)$ , $(3)$ , $(4)$ .

Rua0Fpx4JSMfc

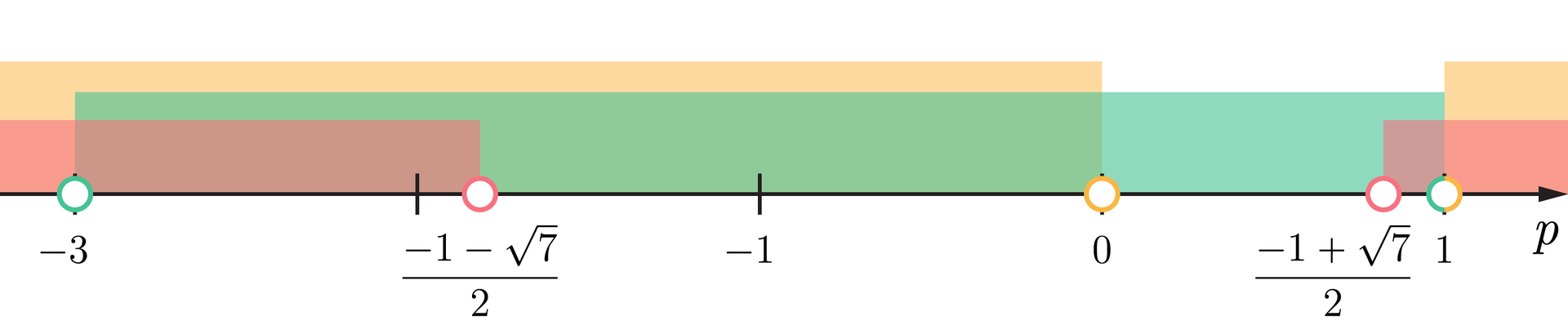
Ilustracja przedstawia poziomą oś p z zaznaczonymi na niej następującymi liczbami od lewej: -3, -1-72, -1, 0, -1+72, 1. Na osi zaznaczono następujące przedziały: -∞,-1-72, -∞,0, -3, 1, -1+72,+∞, 1, +∞.

Ostatecznie: $p \in (- 3, \frac{- 1 - \sqrt{7}}{2})$ .

Słownik

równanie kwadratowe zupełne

równanie postaci:

a x^{2} + b x + c = 0,

gdzie:
$a$ , $b$ i $c$ – są dowolnymi liczbami rzeczywistymi różnymi od zera

Wprowadzenie

Galeria zdjęć interaktywnych

Słownik