Przeczytaj
Kąt między dwiema prostymi
Zaczniemy rozważania od wyznaczenia procedury obliczania miary kąta między dwiema prostymikąta między dwiema prostymi. Załóżmy, że mamy dane dwie proste o równaniach : i : , przecinające się w punkcie . Pamiętamy, że ich współczynniki kierunkowe, i , są jednocześnie wartościami tangensów kątów pomiędzy prostymi i a osią . Łatwo zobaczyć, że miara kąta pomiędzy prostymi jest równa różnicy miar kątów między tymi prostymi a osią .
Oznaczmy: i .
Ze wzoru na tangens różnicy kątów możemy wywnioskować, że tangens kąta między prostymi wynosi:
Na zakończenie zauważmy, że czasami możemy otrzymać ujemną wartość miary kąta, co oznaczałoby, że znaleźliśmy kąt rozwarty pomiędzy naszymi prostymi, zatem wygodniej jest w powyższych wzorach używać wartości bezwzględnej, to znaczy przyjąć
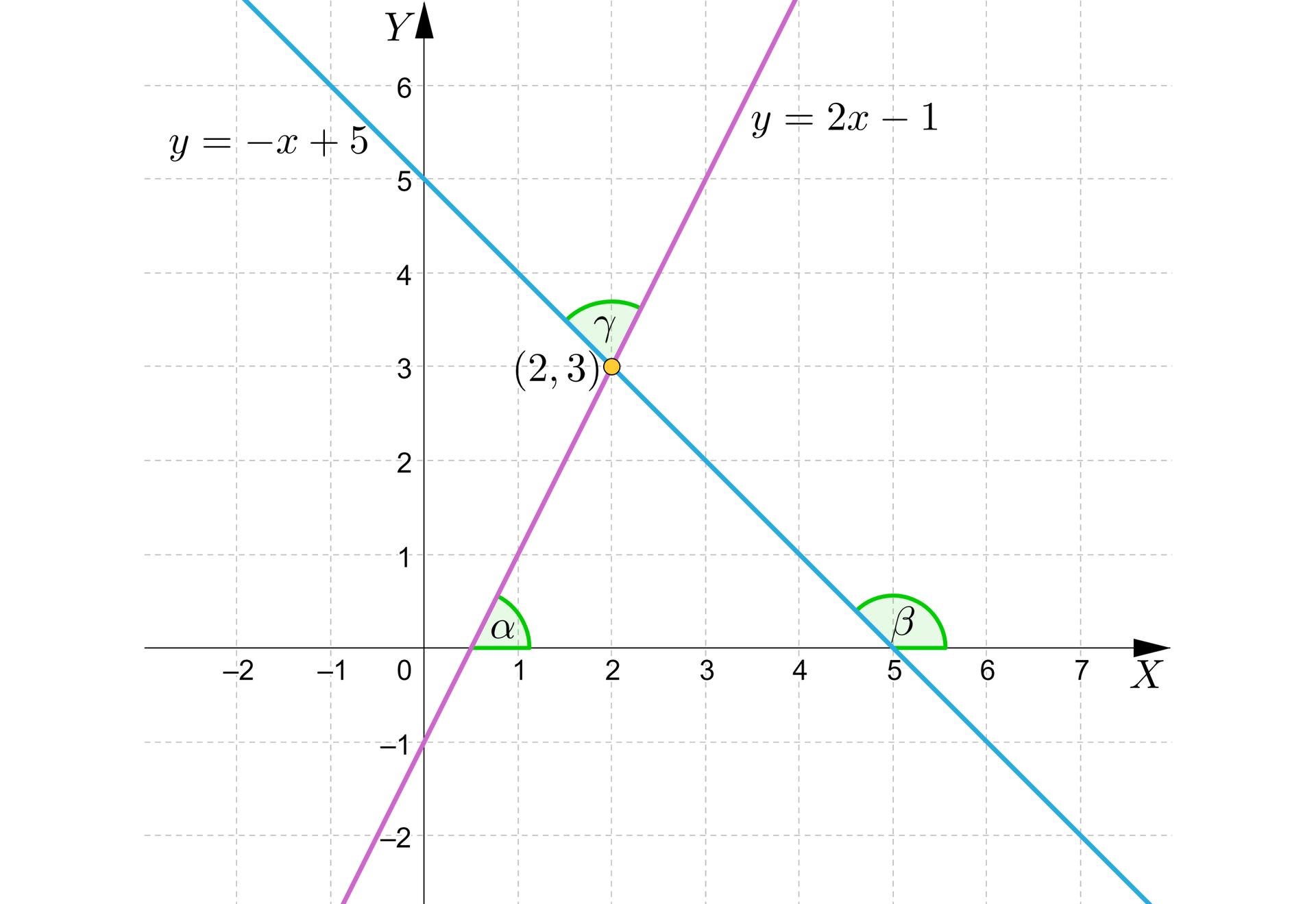
Rozważmy proste i , przecinające się w punkcie . Wyznaczymy miarę kąta ich przecięcia.
Rozwiązanie
Tangens kąta pomiędzy prostymi i jest równy:
,
czyli miara kąta między tymi prostymi wynosi około .
Kąt między wykresami dwóch funkcji
W matematyce, w wielu przypadkach definiujemy nowe, trudne pojęcia, używając prostszych, dobrze znanych – za przykład może posłużyć chociażby pojęcie granicy funkcji, które opiera się na granicy ciągu liczbowego. Miarę kąta między wykresami funkcji definiujemy jako miarę kąta pomiędzy stycznymi do tych krzywych.
Przypomnijmy, że styczna do krzywejstyczna do krzywej w danym punkcie to prosta, która w małym otoczeniu tego punktu ma przebieg podobny do przebiegu krzywej oraz ma w tym otoczeniu dokładnie jeden punkt wspólny z krzywą. Jeżeli zatem mamy funkcję różniczkowalną i punkt , należący do jej wykresu, to równanie stycznej jest postaci:
Dla naszych celów potrzebować będziemy jedynie współczynników kierunkowych prostych stycznych, czyli wartości pochodnych danych funkcji w zadanym punkcie.
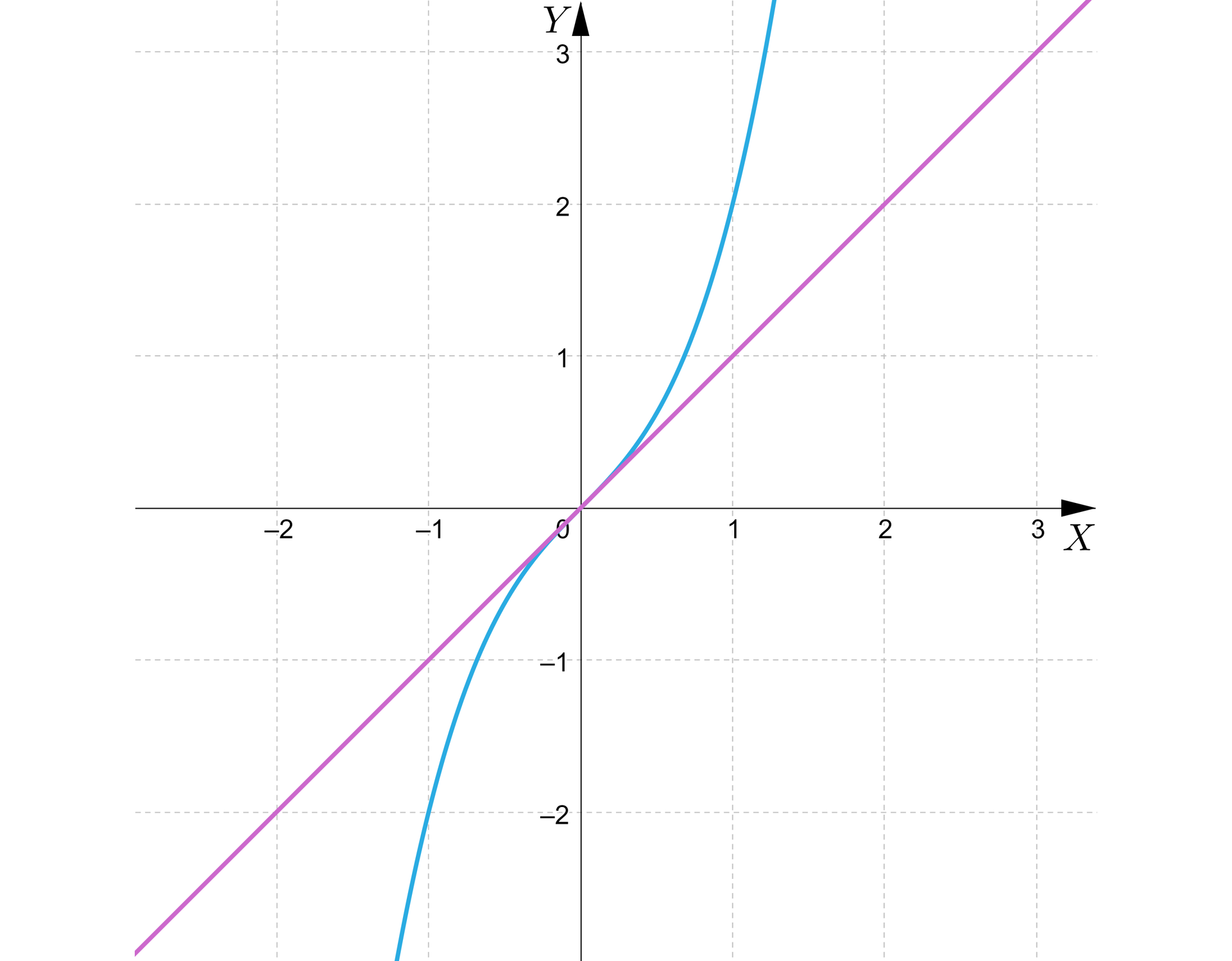
Wyznaczymy miarę kąta pomiędzy wykresem funkcji a osią w punkcie .
Rozwiązanie
Pochodna funkcji ma postać: , więc współczynnik kierunkowy stycznej jest równy .
Oś opisujemy równaniem: , czyli jej współczynnik kierunkowy: .
Tangens kąta pomiędzy funkcją a osią w punkcie jest równy:
,
czyli miara kąta między tymi prostymi wynosi .
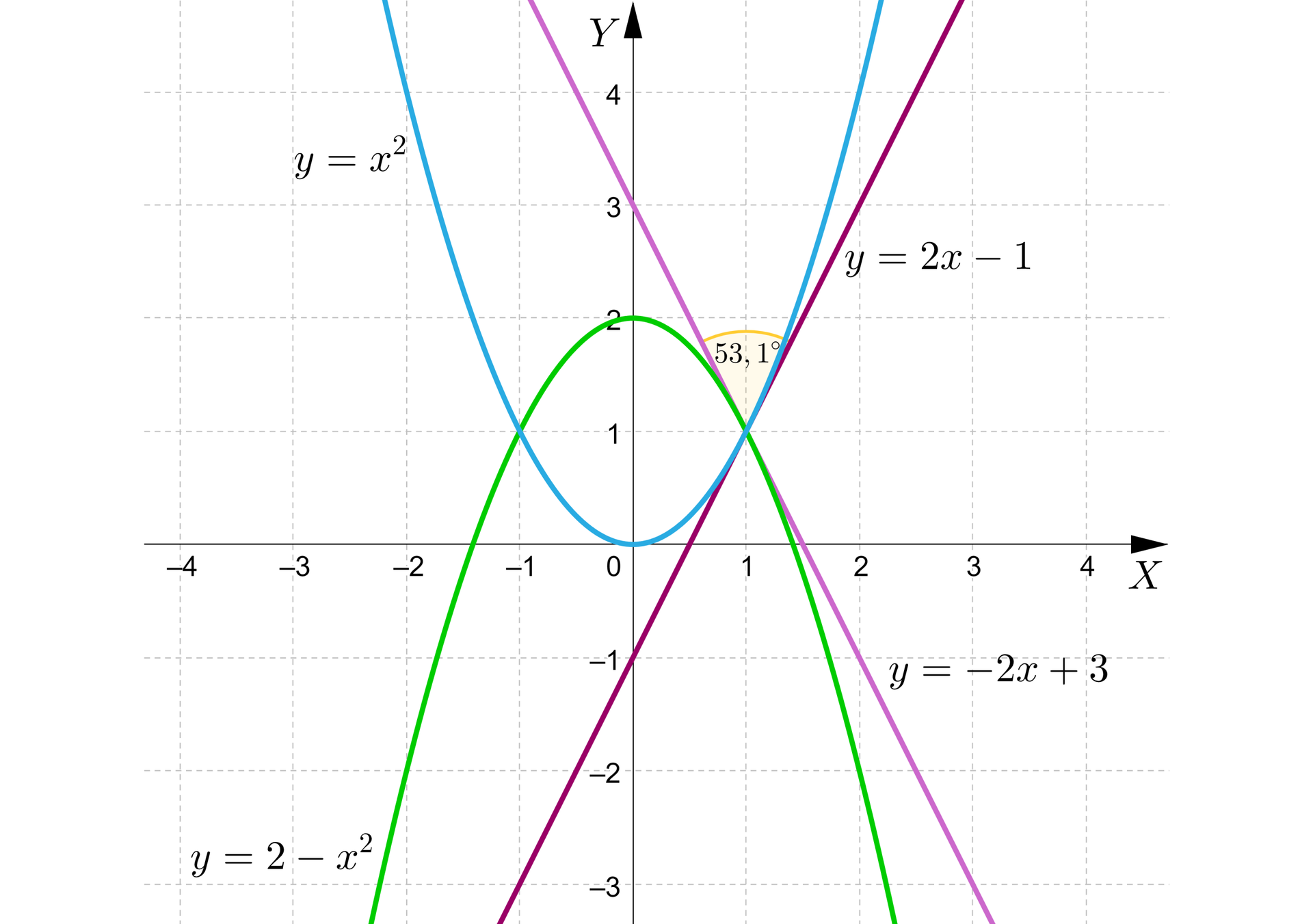
Wyznaczymy miarę kąta pomiędzy wykresami funkcjikąta pomiędzy wykresami funkcji i .
Rozwiązanie
Parabole te mają dwa punkty przecięcia: i .
Ponieważ obliczenia w obu punktach by się pokrywały, dla uproszczenia wybierzemy punkt .
Pochodna funkcji jest postaci: , a funkcji : .
W punkcie współczynniki kierunkowe stycznych są równe: i .
Stąd możemy wyznaczyć wartość tangensa kąta pomiędzy wykresami tych funkcji w punkcie , to znaczy:
,
oraz miarę tego kąta około: .
Wyznaczymy miarę kąta, pod którym przecina się wykres funkcji kwadratowej oraz wykres funkcji liniowej .
Rozwiązanie
Najpierw musimy wyznaczyć punkty przecięcia tych wykresów. W tym celu musimy rozwiązać równanie .
Ma ono dwa rozwiązania: i .
W obydwu przypadkach wyznaczymy odpowiednie kąty przecięcia.
Pochodna funkcji wynosi , więc jej wartość w punkcie będzie równa , a w punkcie będzie równa .
W obu przypadkach badamy przecięcie z tą samą prostą, o współczynniku kierunkowym równym .
W pierwszym przypadku tangens kąta przecięcia wynosi:
, czyli miara kąta jest równa około .
W drugim przypadku tangens jest równy: ,
czyli miara kąta wynosi około: .
Wyznaczanie funkcji o zadanych kątach przecięcia wykresów
Rozpatrzmy dwie parabole: jedną o równaniu , a drugą – o równaniu z parametrem : . Wyznaczymy wartość parametru tak, aby kąt przecięcia był prosty i by punkt przecięcia wykresów leżał w pierwszej ćwiartce układu współrzędnych.
Rozwiązanie
Zauważmy, że nie znamy punktu przecięcia wykresów tych funkcji. Uzależnimy zatem wszystkie wyniki od nieznanej wartości , którą na końcu wyznaczymy tak, by kąt pomiędzy parabolami był kątem prostym.
Punkt jest punktem przecięcia wykresów funkcji, gdy jego współrzędne spełniać będą równanie , czyli .
Po przekształceniu otrzymujemy , co daje , tym samym lub .
Jeśli punkt przecięcia należy do pierwszej ćwiartki układu współrzędnych, to: .
Pochodne funkcji i są równe odpowiednio: i , zatem współczynniki kierunkowe stycznych w punkcie styczności wynoszą i .
Stąd możemy wyznaczyć wartość tangensa kąta pomiędzy wykresami tych funkcji w punkcie :
.
Szukamy takich parabol, żeby kąt pomiędzy nimi był prosty, ale niestety tangens kąta prostego nie istnieje, zatem nie możemy powtórzyć rozumowania z powyższych przykładów.
Możemy jednak skorzystać z faktu, że dwie proste są prostopadłe, gdy iloczyn ich współczynników kierunkowych będzie równy .
W naszym przypadku prowadzi nas to do równania , czyli .
Stąd otrzymujemy i .
Poszukiwania parametru możemy spróbować wykonać graficznie, na przykład używając apletu.
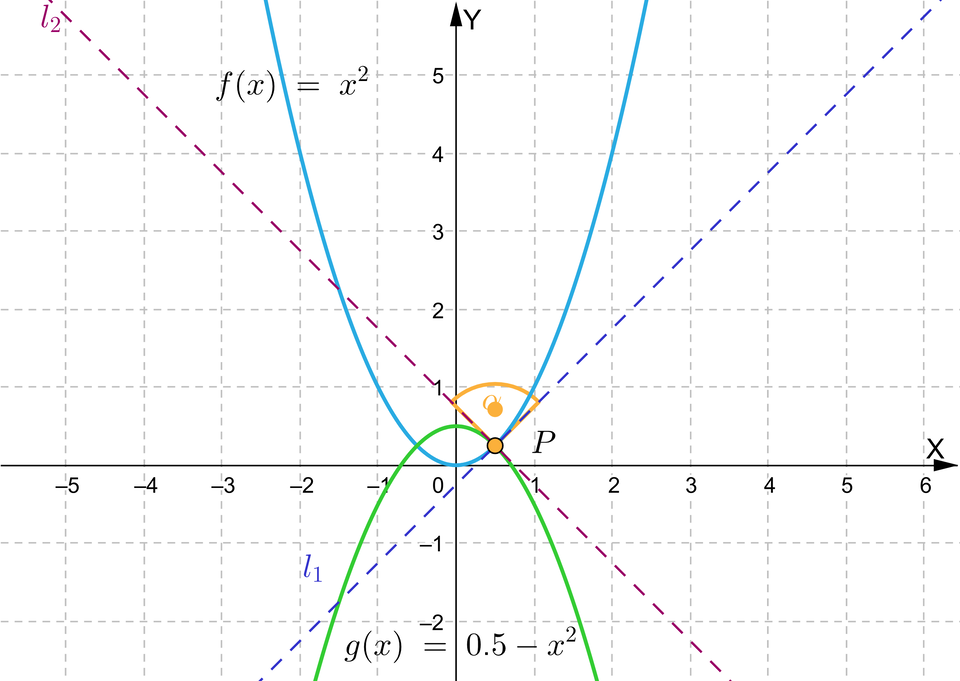
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DY0qk5kfb
Słownik
wartość bezwzględna różnicy miar kątów, jakie te proste tworzą z osią
kąt pomiędzy stycznymi do danych wykresów funkcji w punkcie przecięcia
prosta, która w małym otoczeniu tego punktu ma przebieg zbliżony do przebiegu krzywej oraz ma w tym otoczeniu dokładnie jeden punkt wspólny z krzywą