Styczną do okręgustyczna do okręguStyczną do okręgu nazywamy prostą, która ma dokładnie jeden punkt wspólny z tym okręgiem. Punkt ten nazywamy punktem styczności.

R1ZCflQTudLDT

Rysunek przedstawia okrąk o środku w punkcie $S$ i promieniu $r$ oraz ukośną prostą styczną do tego okręgu. Na ilustracji wyróżniono zamalowanym kółkiem punkt styczności $P$ i podpisano go. Ze środka okręgu poprowadzono promień do punktu $P$ oraz zaznaczono kąt prosty między promieniem a prostą przy wierzchołku $P$.

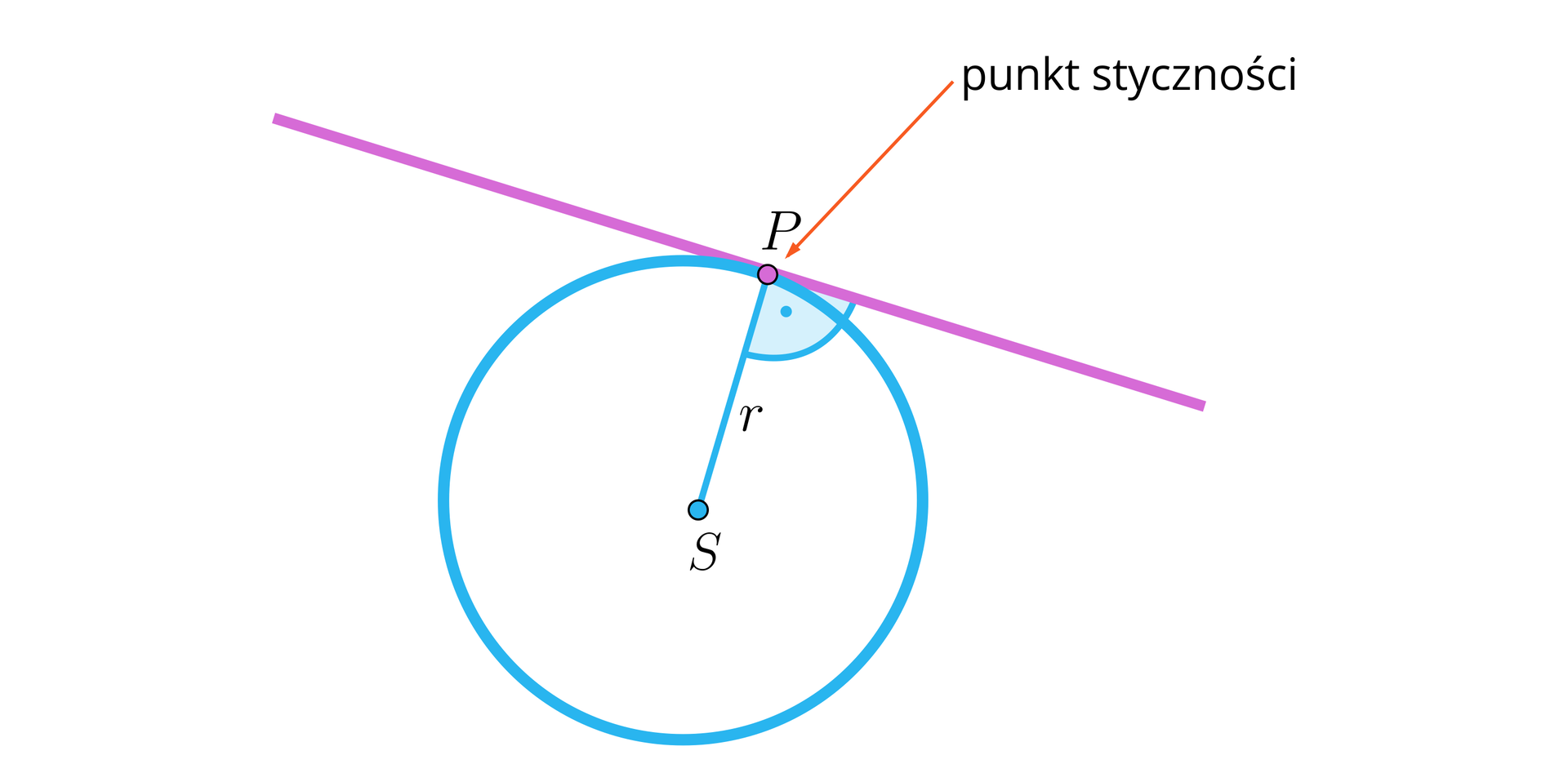
Styczna do okręgustyczna do okręguStyczna do okręgu jest prostopadła do promienia łączącego punkt styczności i środek okręgu.

Wyznaczymy równanie stycznej do okręgu o równaniu ${\left(x+1\right)}^2+{\left(y-3\right)}^2=5$, przechodzącej przez punkt $\left(1,2\right)$.

Z równania okręgu możemy odczytać środek $S=\left(-1,3\right)$ oraz promień $r=\sqrt{5}$.

Styczna do okręgu ma równanie $y=ax+b$.

Ponieważ punkt $\left(1,2\right)$ należy do tej prostej, zatem otrzymujemy równanie $2=a+b$, więc $b=2-a$.

Prosta jest postaci $y=ax+2-a$, co po przekształceniu do postaci ogólnej daje $ax-y+2-a=0$.

Wykorzystamy wzór na odległość punktu od prostej $d=\frac{\left|Ax+By-C\right|}{\sqrt{A^2+B^2}}$ oraz fakt, że odlegość środka okręgu od podanego punktu jest równa długości promienia okręgu.

Zatem mamy równanie $\frac{\left|-a-3+2-a\right|}{\sqrt{a^2+1}}=\sqrt{5}$.

Po przekształceniu równania otrzymujemy, że $\left|-2a-1\right|=\sqrt{5}\sqrt{a^2+1}$.

Podnosimy obie strony równania do kwadratu i przekształcamy do postaci $a^2-4a+4=0$, co daje ${\left(a-2\right)}^2=0$, więc $a=2$.

Otrzymujemy, że $b=0$.

Zatem szukana styczna jest postaci $y=2x$.

Wyznaczymy równanie stycznej do okręgu o równaniu ${\left(x-3\right)}^2+{\left(y+2\right)}^2=25$, przechodzącej przez punkt $\left(0,2\right)$.

Prosta styczna jest postaci $y=ax+b$.

Ponieważ punkt $\left(0,2\right)$ należy do tej prostej, zatem jest ona postaci $y=ax+2$.

Rozwiążemy układ równań $\left\{\begin{array}{l}{\left(x-3\right)}^2+{\left(y+2\right)}^2=25\\ y=ax+2\end{array}\right.$.

Aby prosta była styczna do okręgu, to układ musi mieć jedno rozwiązanie.

Po podstawieniu otrzymujemy równanie ${\left(x-3\right)}^2+{\left(ax+4\right)}^2=25$

Po uporządkowaniu mamy, że $\left(a^2+1\right)x^2+\left(8a-6\right)x=0$. Obliczamy wyróżnik, który musi wynosić $0$, zatem mamy równanie ${\left(8a-6\right)}^2=0$.

Z równania wynika, że $a=\frac{3}{4}$.

Zatem szukana styczna jest postaci $y=\frac{3}{4}x+2$.

Wyznaczymy równanie stycznej do okręgu ${\left(x-2\right)}^2+y^2=10$, przechodzącej przez punkt $\left(1,3\right)$.

Z równania okręgu możemy odczytać, że $S=\left(2,0\right)$ oraz $r=\sqrt{10}$.

Ponieważ styczna jest prostopadła do promienia okręgu w punkcie styczności, wyznaczymy równanie prostej prostopadłej.

Prosta przechodząca przez punkty $\left(1,3\right)$ i $\left(2,0\right)$ ma współczynnik kierunkowy równy $a=-3$.

Zatem współczynnik kierunkowy stycznej wynosi $a=\frac{1}{3}$.

Styczna przechodzi przez punkt $\left(1,3\right)$, zatem mamy równanie $3=\frac{1}{3}+b$.

Zatem $b=2\frac{2}{3}$.

Równanie szukanej stycznej jest postaci $y=\frac{1}{3}x+2\frac{2}{3}$.

Wyznaczymy równanie stycznej do okręgu o równaniu ${\left(x-2\right)}^2+{\left(y+1\right)}^2=4$, przechodzącej przez punkt $\left(2,1\right)$.

Odczytujemy dane $S=\left(2,-1\right)$, $r=2$ oraz $\left(x_a,y_b\right)=\left(2,1\right)$.

Po podstawieniu do wzoru na równanie stycznej otrzymujemy, że $\left(2-2\right)\left(x-2\right)+\left(1+1\right)\left(y+1\right)=4$.

Zatem równanie stycznej jest postaci $y=1$.

Wyznaczymy dla jakiego parametru $m$ okrąg $x^2+{\left(y+2\right)}^2=m+4$ i prosta $y=2x-1$ mają dokładnie jeden punkt wspólny.

Aby równanie przedstawiało okrąg, to powinien zachodzić warunek $m+4>0$, więc $m\in \left(-4,\infty \right)$.

W celu wyznaczenia wartości parametru rozwiążemy układ równań, w którym jedno równanie jest równaniem okręgu, a drugie równanie opisuje prostą.

Zatem mamy $\left\{\begin{array}{l}{x}^2+{\left(y+2\right)}^2=m+4\\ y=2x-1\end{array}\right.$.

Podstawiamy drugie równanie do pierwszego równania w miejsce niewiadomej $y$. Otrzymujemy równanie $x^2+{\left(2x+1\right)}^2=m+4$, co po przekształceniu daje równanie $5x^2+4x-m-3=0$.

Aby prosta i okrąg miały dokładnie jeden punkt wspólny, to wyróżnik musi być równy $0$.

Obliczamy $∆=16-20·\left(-m-3\right)=76+20m$.

Z równania $∆=0$ oraz po uzgodnieniu z założeniem otrzymujemy, że $m=-3\frac{4}{5}$.

prosta, która ma dokładnie jeden punkt wspólny z okręgiem

równanie postaci $\left(x_a-a\right)\left(x-a\right)+\left(y_b-b\right)\left(y-b\right)=r^2$, gdzie środek $S=\left(a,b\right)$ oraz $r$ - promień okręgu, $\left(x_a,y_b\right)$ - punkt, przez który przechodzi styczna