Przeczytaj
Wykresem funkcji kwadratowej określonej na zbiorze wzorem
gdzie , , i jest parabolaparabola.
Jeżeli
, to ramiona paraboli, która jest wykresem funkcji kwadratowej są skierowane do dołu,
RVnNZvt86eHPg 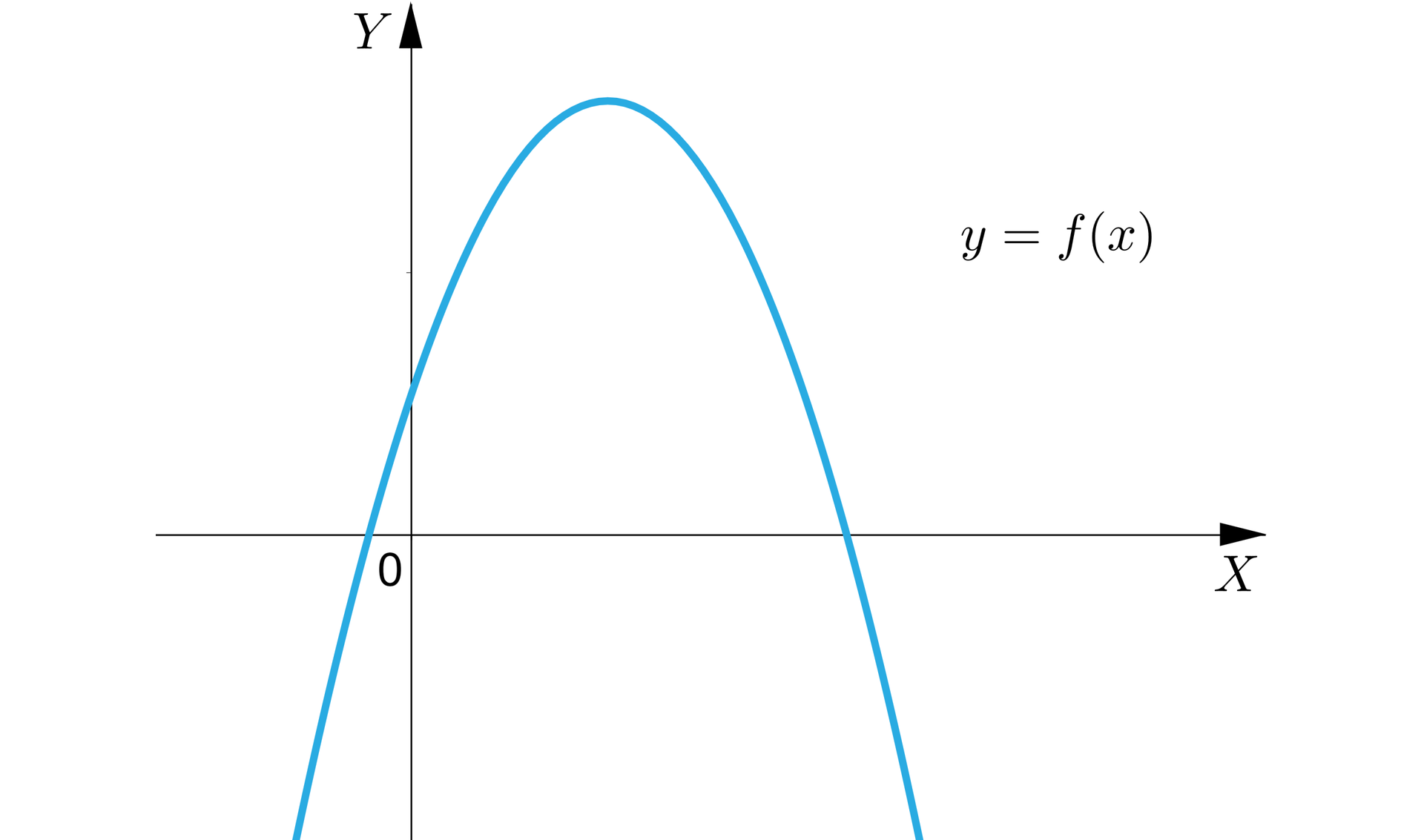
, to ramiona paraboli, która jest wykresem funkcji kwadratowej są skierowane do góry.
R168jdz0NvDPU 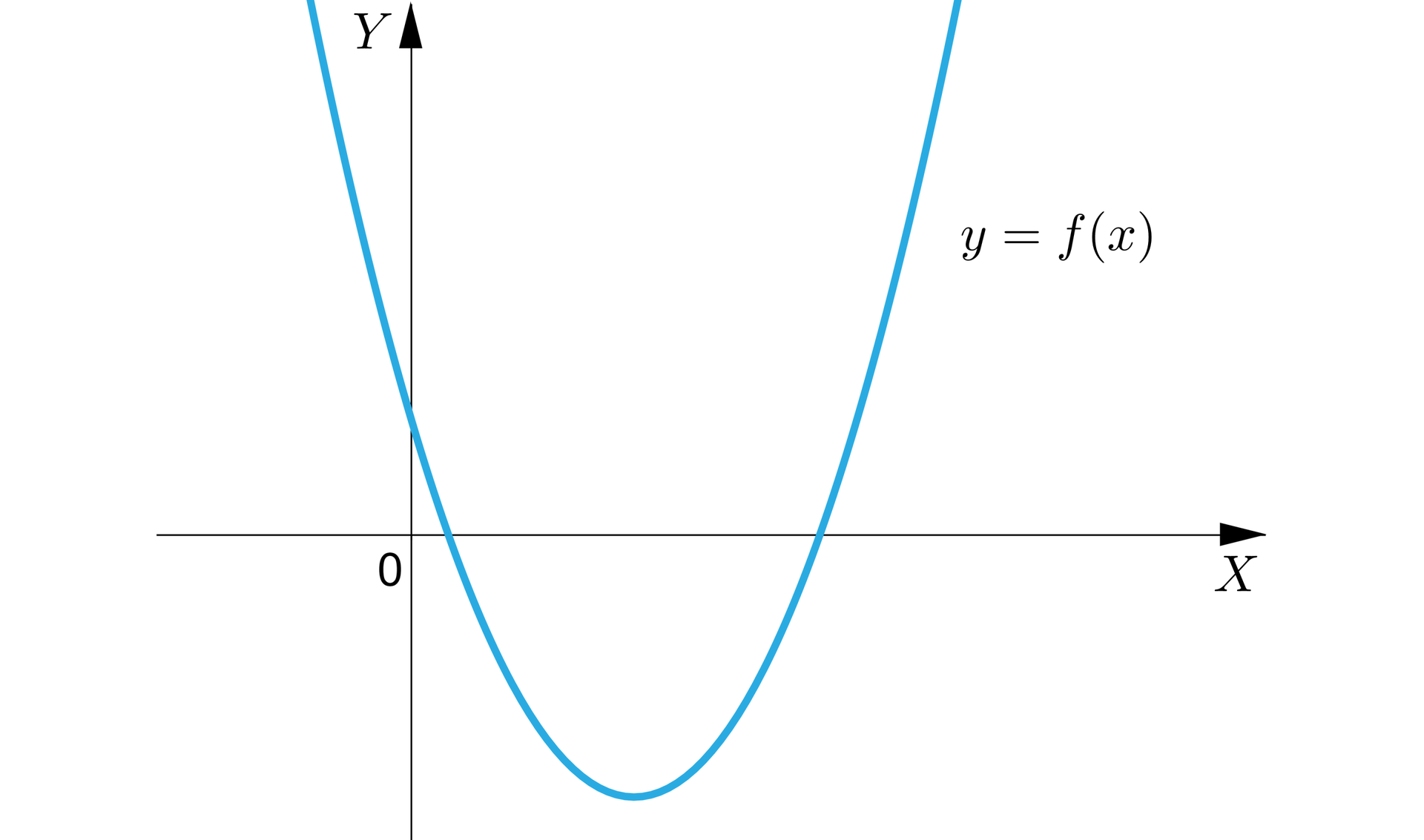
Zdefiniujmy pojęcie osi symetrii wykresu funkcji.
Oś symetrii wykresu funkcji to prosta, względem której ten wykres jest sam do siebie symetryczny.
Oś symetrii paraboli – wykresu funkcji kwadratowej
Jeżeli funkcja kwadratowa jest określona wzorem
gdzie , , i , a wierzchołkiem paraboli, która jest wykresem tej funkcji kwadratowej jest punkt o współrzędnych , to osią symetrii wykresu tej funkcji jest prosta o równaniu
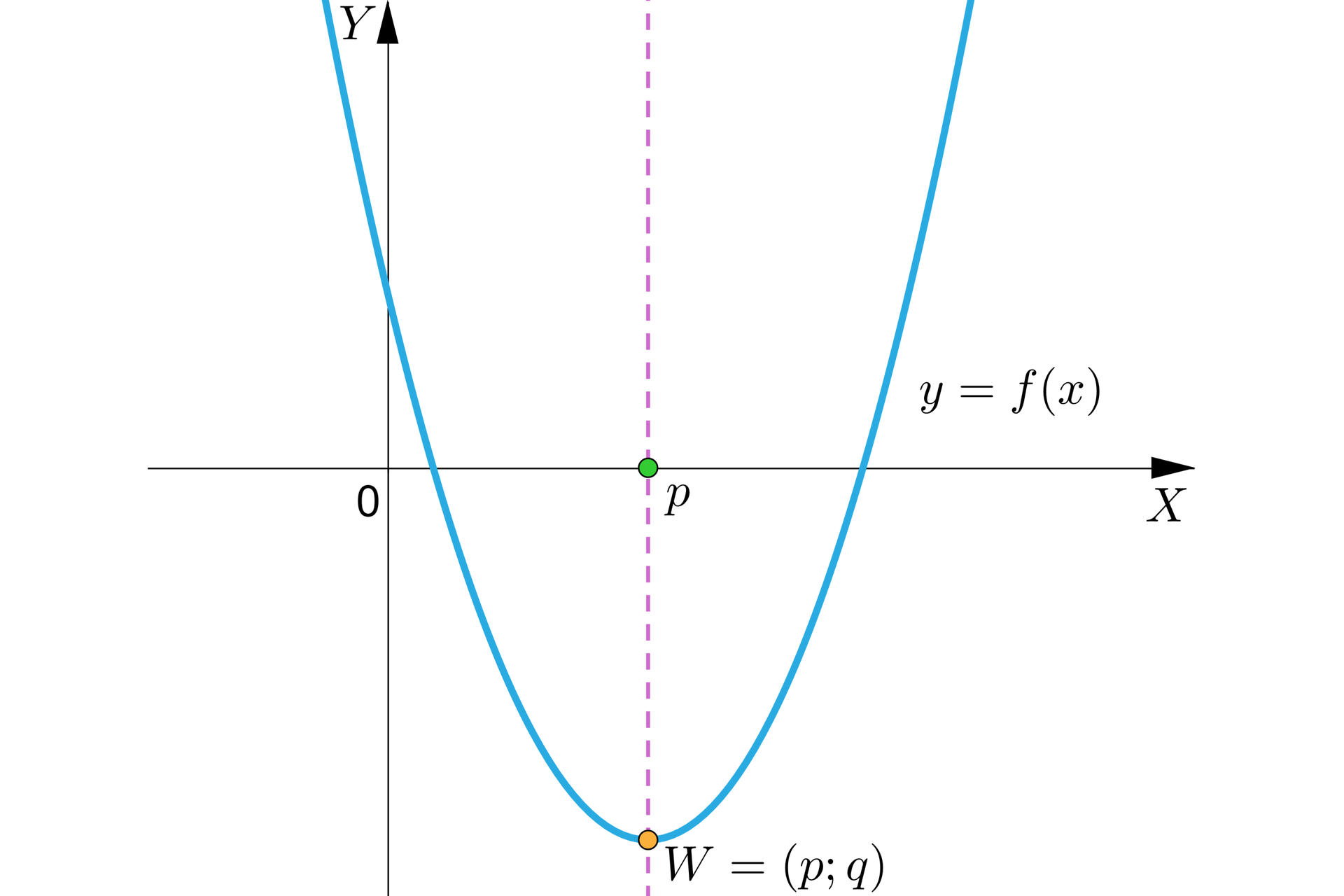
Wzór na równanie osi symetrii wykresu funkcji kwadratowej nie zależy od położenia ramion paraboli.
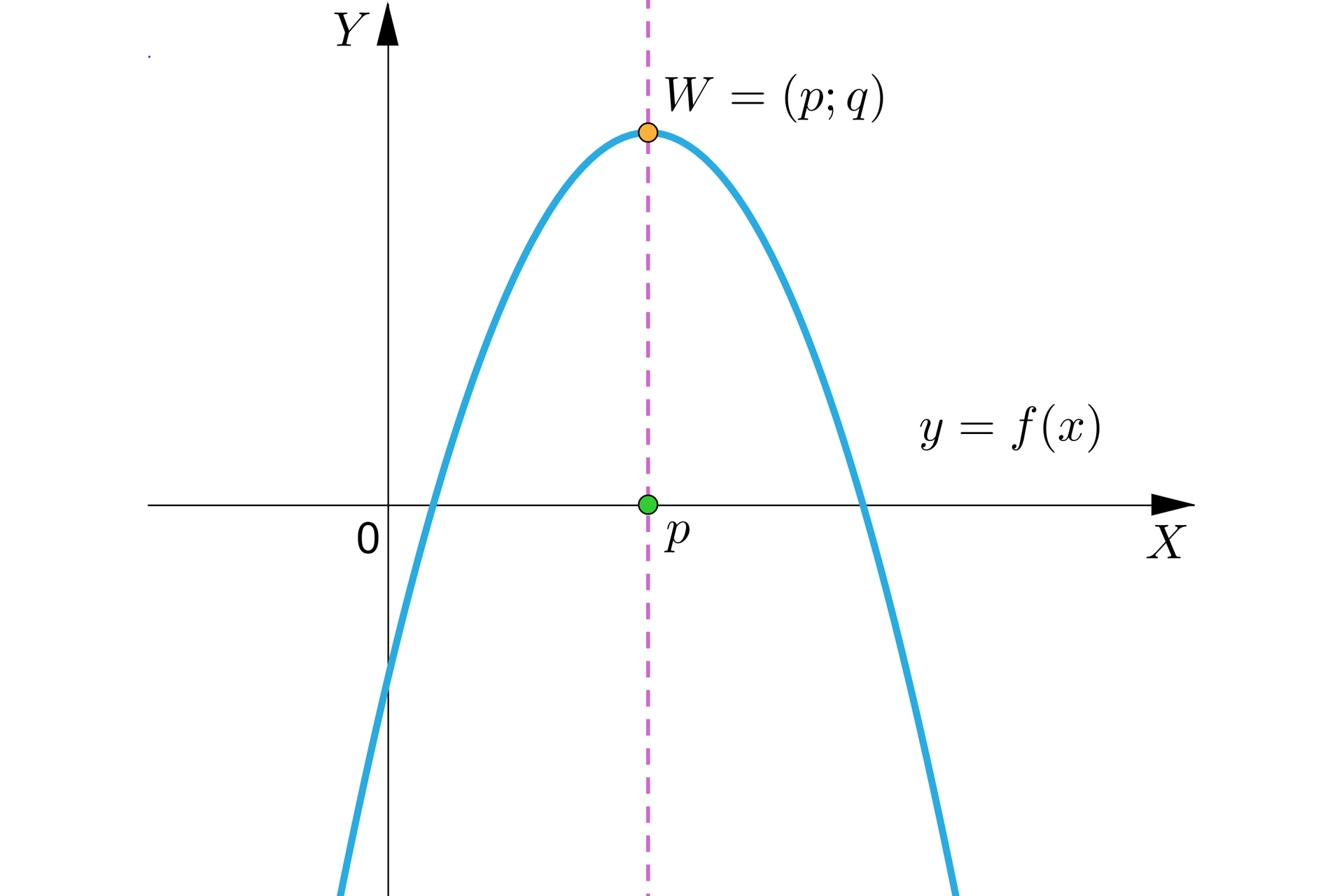
Oś symetrii wykresu funkcji kwadratowej jest zawsze równoległa do osi układu współrzędnych.
Wyznaczymy równanie osi symetrii wykresu funkcji kwadratowej określonej wzorem:
a)
b)
Rozwiązanie:
a) oraz , zatem
b) oraz , zatem
Jeżeli funkcja kwadratowafunkcja kwadratowa jest określona za pomocą wzoru w postaci kanonicznej , to bez wykonywania obliczeń możemy wyznaczyć równanie osi symetrii jej wykresu.
Wyznaczymy równanie osi symetrii wykresu funkcji kwadratowej określonej wzorem:
a)
b)
c)
Rozwiązanie:
Za każdym razem odczytujemy wartość współczynnika , zatem osią symetrii wykresu funkcji jest prosta o równaniu:
a)
b)
c)
Zauważmy, że jeśli do wykresu funkcji kwadratowej określonej wzorem należą punkty, których pierwsze współrzędne to odpowiednio i oraz punkty te leżą po obu stronach osi symetrii wykresu, w równych odległościach od jej wierzchołka, to równanie osi symetrii wykresu takiej funkcji kwadratowej opisujemy za pomocą wzoru
Do wykresu funkcji kwadratowej należą punkty o współrzędnych oraz . Wyznaczymy równanie osi symetrii paraboli, która jest wykresem tej funkcji.
Rozwiązanie:
Jeżeli do wykresu funkcji kwadratowej należą punkty o współrzędnych oraz , to korzystając z powyższej własności równanie osi symetrii jest postaci:
Na rysunku przedstawiono wykresy funkcji kwadratowych , , i .

Odczytamy równania osi symetrii wykresów tych funkcji.
Rozwiązanie:
Równania osi symetrii tych funkcji są określone poniższymi wzorami:
dla wykresu funkcji : ,
dla wykresu funkcji : ,
dla wykresu funkcji : ,
dla wykresu funkcji : .
Wyznaczymy, dla jakich wartości parametru m osią symetrii wykresu funkcji kwadratowej określonej wzorem jest prosta o równaniu .
Rozwiązanie:
Wartości współczynników ze wzoru funkcji kwadratowej wynoszą odpowiednio:
Zatem oś symetrii paraboli, która jest wykresem funkcji kwadratowej opisuje równanie:
Wobec tego do wyznaczenia wartości parametru rozwiązujemy równanie:
oraz
Wobec tego .
Wyznaczymy, dla jakich wartości parametru równaniem osi symetrii wykresu funkcji kwadratowej określonej wzorem jest prosta, która leży w i ćwiartce układu współrzędnych.
Rozwiązanie:
Wartości współczynników ze wzoru funkcji kwadratowej wynoszą odpowiednio:
Zatem oś symetrii paraboli, która jest wykresem funkcji kwadratowej opisuje równanie:
Jeżeli oś symetrii wykresu tej funkcji leży w i ćwiartce układu współrzędnych, to do wyznaczenia wartości parametru rozwiązujemy nierówność:
Zatem , czyli .
Do wykresu funkcji kwadratowej określonej wzorem , gdzie , , oraz należą punkty o współrzędnych , oraz . Wyznaczymy równanie osi symetrii wykresu tej funkcji.
Rozwiązanie:
Jeżeli do wykresu funkcji kwadratowej należą punkty o współrzędnych , oraz , to do wyznaczenia wartości współczynników , , rozwiązujemy układ równań:
Zatem osią symetrii paraboli, która jest wykresem funkcji jest prosta o równaniu:
Wyznaczymy równanie osi symetrii wykresu funkcji określonej wzorem .
Rozwiązanie:
Zauważmy, że wzór funkcji możemy zapisać w następującej postaci:
Wykres tej funkcji przedstawiono na poniższym rysunku.
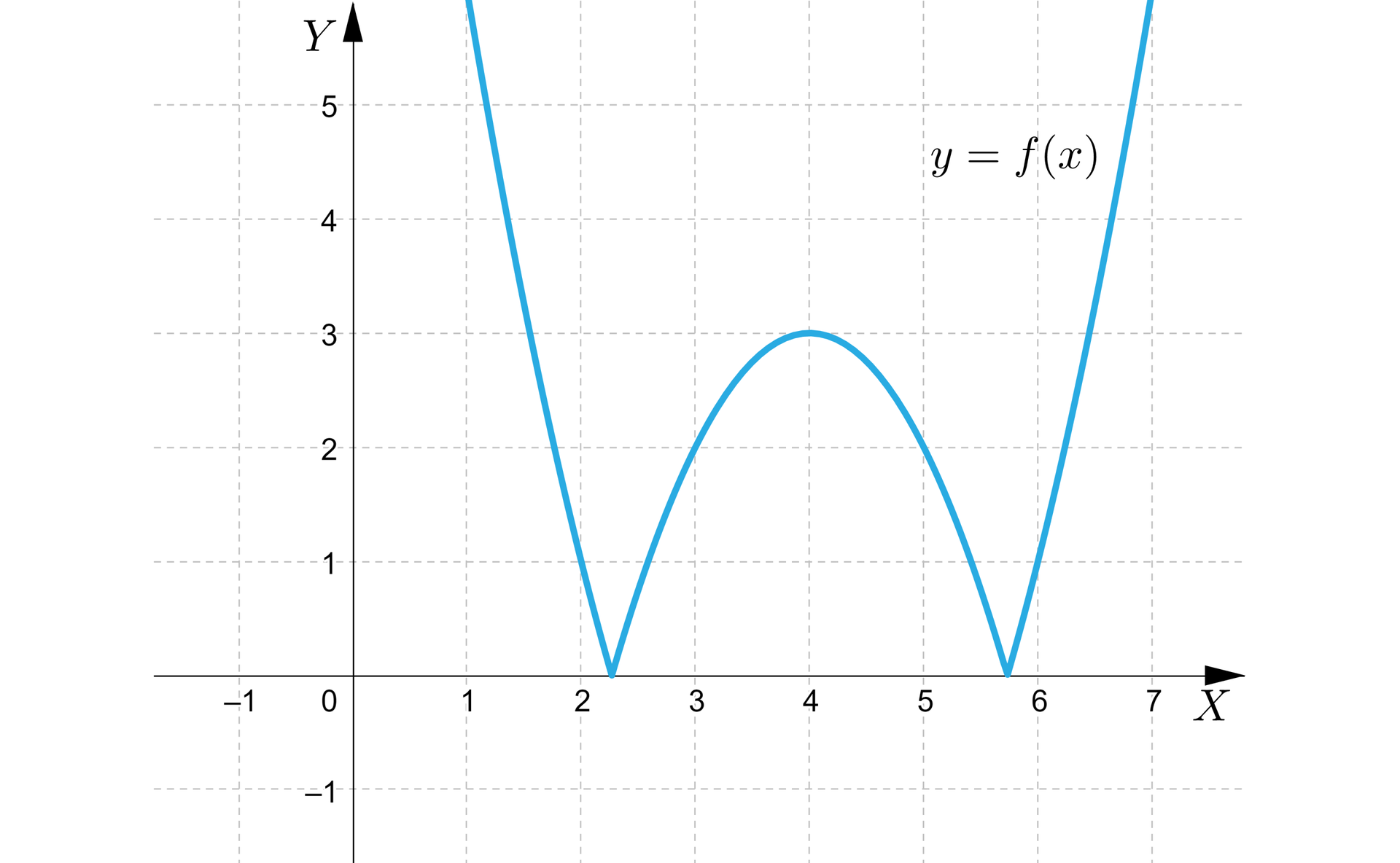
Zatem osią symetrii wykresu tej funkcji jest prosta o równaniu .
Słownik
wykres funkcji kwadratowej
funkcja określona wzorem
gdzie , , i