Przeczytaj
Ucząc się stereometrii spotkaliśmy się już z kątem między prostą a płaszczyzną. W tym materiale omówimy niełatwy, ale kluczowy moment w wielu zadaniach ze stereometrii, a mianowicie moment, w którym musimy zaznaczyć właściwy kąt w podanej bryle. Zajmiemy się oczywiście ostrosłupami.
Wykorzystaj poniższy aplet, aby zaobserwować, jak zaznaczyć w ostrosłupie kąt między krawędzią boczną ostrosłupa a płaszczyzną jego podstawy. Jest to jeden z najczęściej występujących kątów w zadaniach. Zmieniając położenie suwaka możesz obserwować różne nachylenia krawędzi bocznej ostrosłupa do jego podstawy.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfBWskNyM
Powyższy aplet przedstawia jedynie obserwacje dotyczące kąta między krawędzią boczną a podstawą ostrosłupa prawidłowego. Możemy jednak analogicznie pracować na kącie między wysokością ściany bocznej poprowadzonej z wierzchołka (tzw. apotemą) a podstawą ostrosłupa:
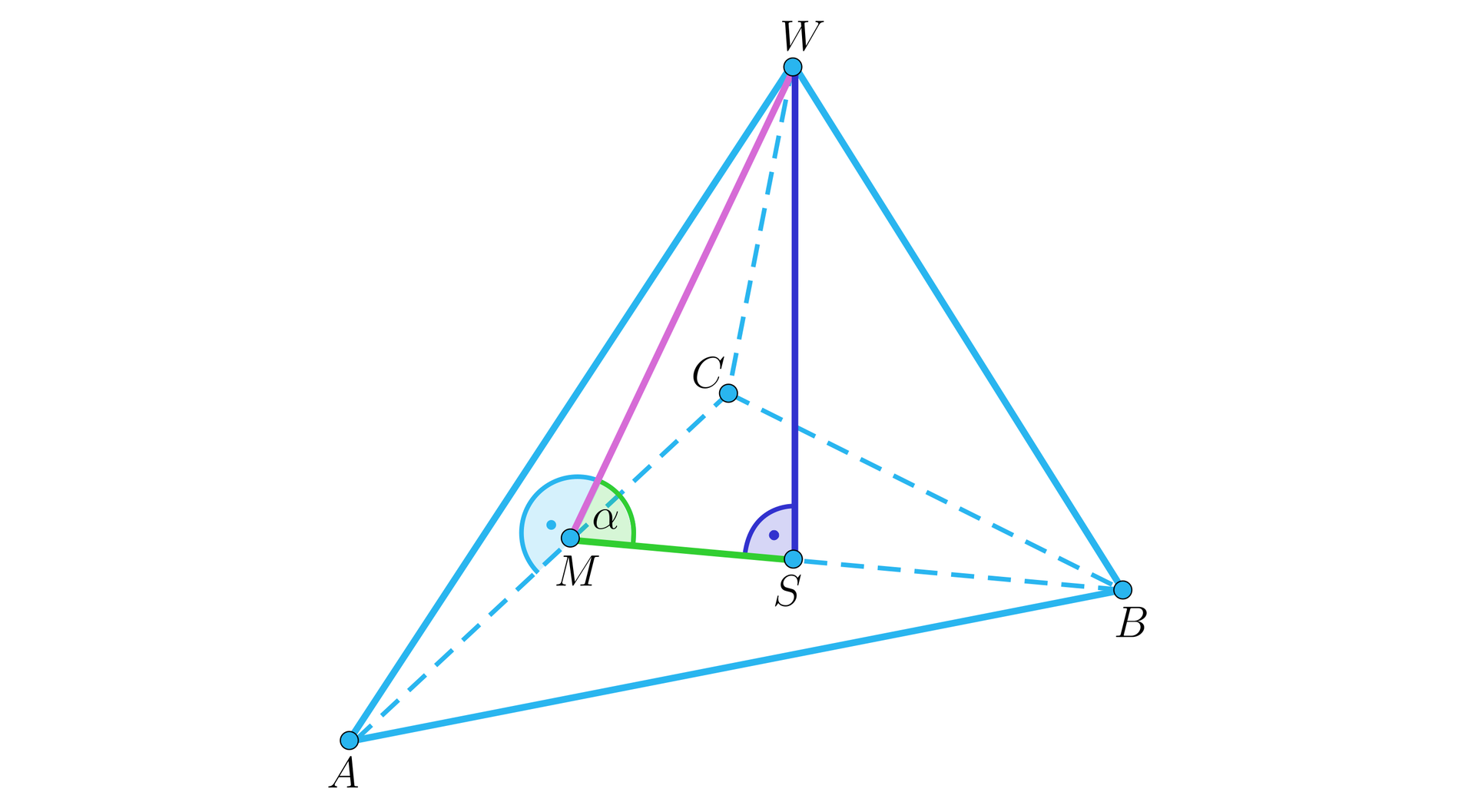
albo między wysokością ostrosłupa a jego ścianą boczną:
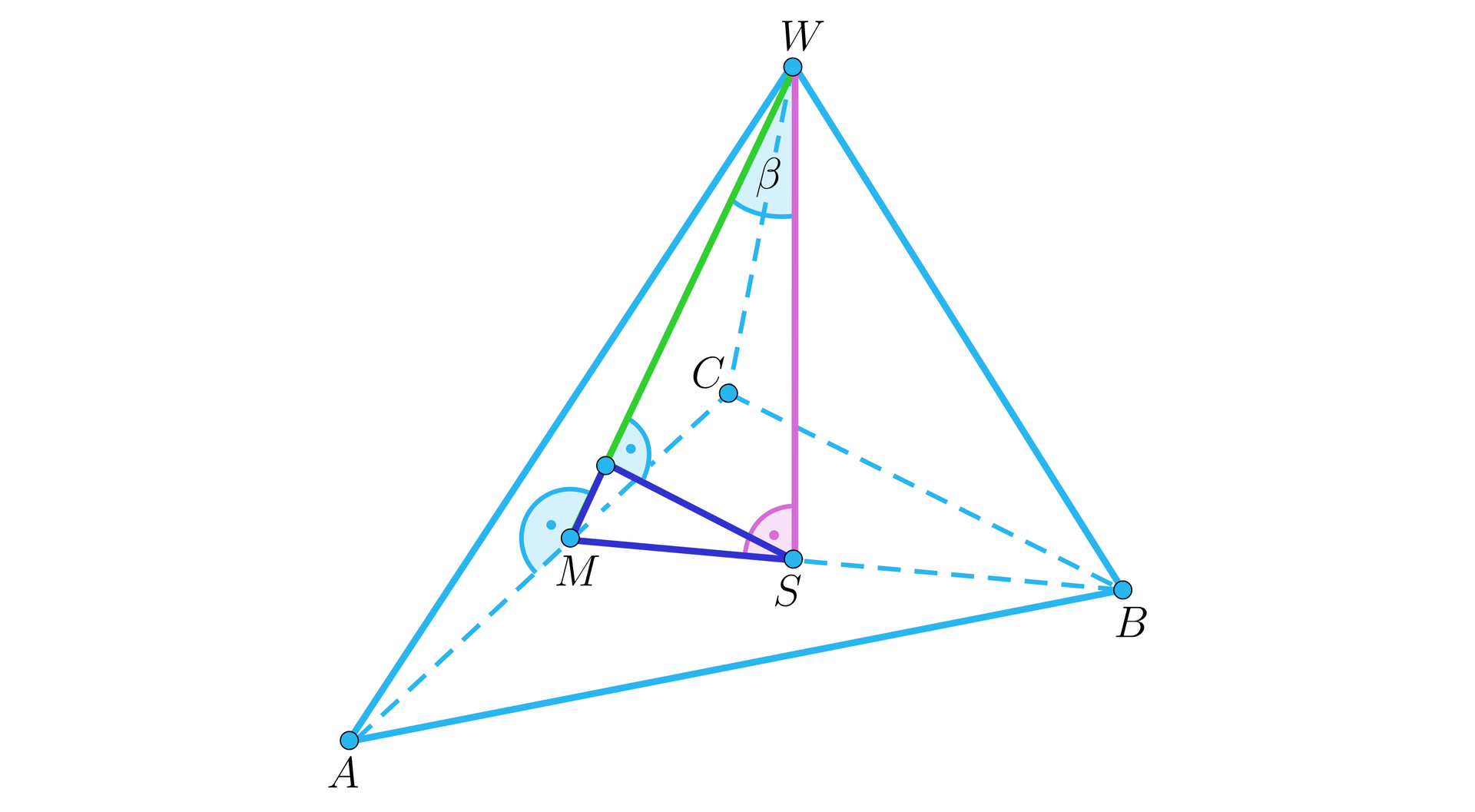
W każdym z tych przypadków musimy pamiętać, aby starannie przemyśleć, co jest rzutem prostokątnym danej prostej na wskazaną płaszczyznę. Aby ułatwić ten proces, na powyższych rysunkach każdorazowo na różowo zaznaczono odcinek uwzględniony w definicji kąta a na zielono jego rzut prostokątny na ścianę.
Jednocześnie w zadaniach skupionych na wyznaczaniu miar pewnych kątów często mamy do czynienia z sytuacją, gdy autor zadania nie podaje nam żadnej danej długości odcinka. Do kłopotów z interpretacją opisanego kąta dochodzi wówczas problem pracy na wyrażeniach algebraicznych, w których finalnie muszą skrócić się wszystkie przyjęte przez nas oznaczenia literowe długości poszczególnych odcinków. Przeanalizujmy kilka przykładów, aby zapoznać się z najczęściej stosowanymi metodami pracy w zadaniach dotyczących kątów między prostymi a płaszczyznami w ostrosłupach.
Narysujemy ostrosłup prawidłowy trójkątny o podstawie i wierzchołku . Zaznaczymy kąt nachylenia krawędzi bocznej do płaszczyzny podstawy. Wiedząc, że jest on równy kątowi między krawędziami bocznymi i tego ostrosłupa, obliczymy miarę kąta .
Rozwiązanie:
Zaczniemy oczywiście od rysunku:
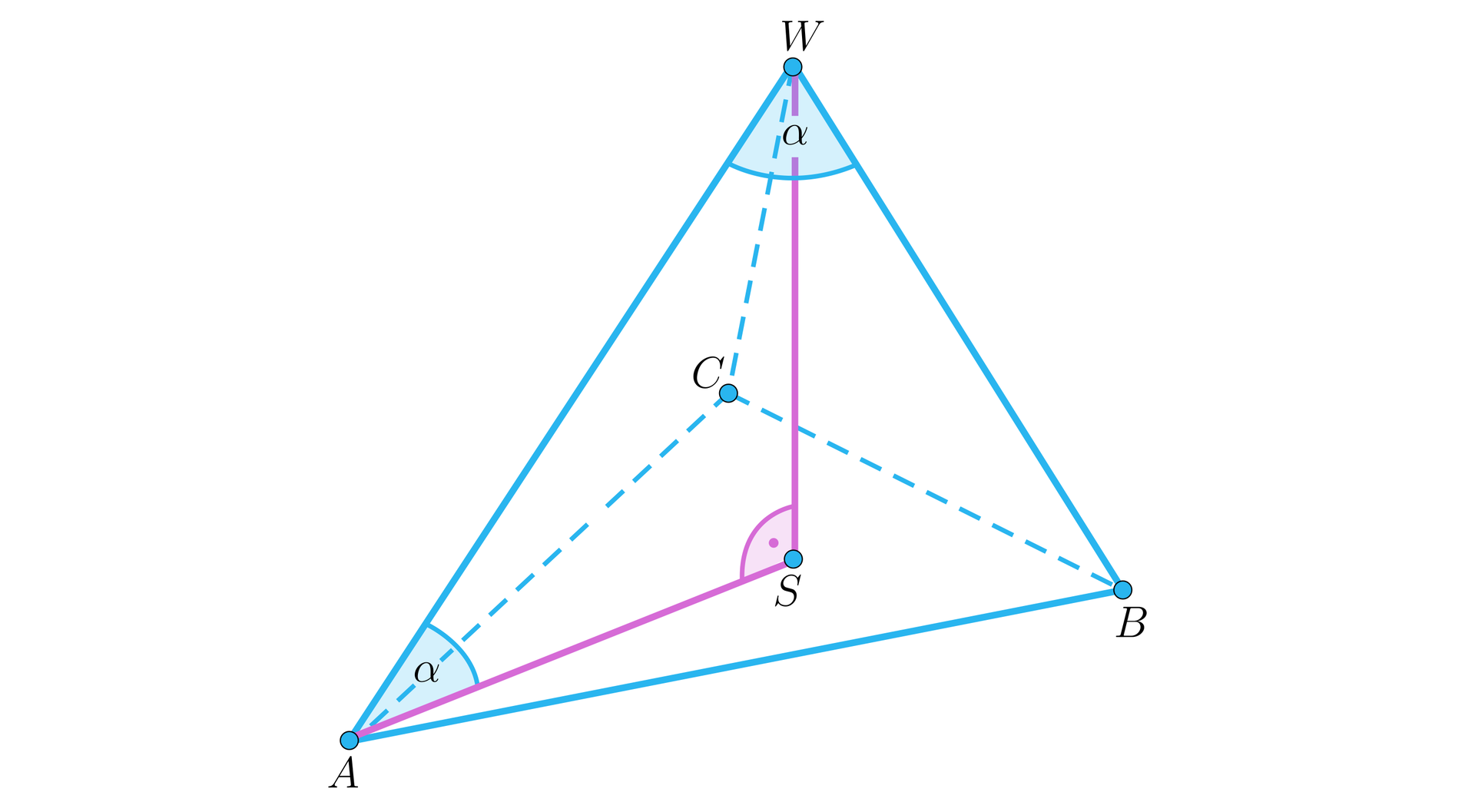
Aby zaznaczyć kąt nachylenia krawędzi bocznej do płaszczyzny podstawy, określamy najpierw rzut prostokątny tej krawędzi na podstawę. Punkt już do niej należy, natomiast rzutem prostokątnym punktu na podstawę jest oczywiście spodek wysokości ostrosłupa. Ostatecznie opisany w zadaniu kąt to kąt . Aby wyznaczyć miarę tego kąta wykorzystamy definicję funkcji trygonometrycznej cosinus w trójkącie prostokątnym . Oznaczmy długość krawędzi podstawy ostrosłupa jako , zaś długość jego krawędzi bocznej jako :
Wykorzystując informację z tekstu zadania, że kąt jest równy kątowi i stosując twierdzenie cosinusówtwierdzenie cosinusów w trójkącie , otrzymujemy związek:
.
Podstawiając teraz poprzednio otrzymaną zależność między , oraz otrzymujemy:
.
Traktując ostatnie równanie jak równanie kwadratowe o niewiadomej , otrzymujemy:
lub
Ponieważ jednak wartość pierwszego rozwiązania jest mniejsza od , rozpatrujemy jedynie drugie rozwiązanie, które w przybliżeniu jest równe .
Wykorzystując tablice matematyczne, odczytujemy, że kąt , który mieliśmy wyznaczyć, ma w przybliżeniu miarę .
Dany jest ostrosłup prawidłowy sześciokątny . Wiedząc, że tangens kąta nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy jest równy , obliczymy miary kątów wewnętrznych trójkąta , gdzie , są środkami równoległych krawędzi podstawy ostrosłupa.
Rozwiązanie:
Zacznijmy ponownie od rysunku bryły. W przypadku ostrosłupa prawidłowego wszystkie ściany boczne są trójkątami równoramiennymi przystającymi. Stąd nie ma znaczenia, przy których krawędziach zaznaczymy opisane w zadaniu kąty. Ważne jest jedynie poprawne naniesienie na rysunek rzutu prostokątnego krawędzi bocznej na płaszczyznę podstawy.

Ponownie przyjmijmy oznaczenia dla krawędzi podstawy , zaś dla wysokości ostrosłupa . Litery te pojawią się w rozwiązaniu dla poprawienia czytelności przekształceń, nie traktujemy ich jednak jako danych. W końcowej odpowiedzi nie mogą się zatem pojawić.
Wykorzystamy definicję funkcji trygonometrycznej tangens w trójkącie prostokątnym :
.
Zauważmy teraz, że jeżeli jest środkiem krawędzi podstawy, to odcinek jest wysokością trójkąta równobocznego o boku długości . Ostatecznie wykorzystując w trójkącie definicję funkcji trygonometrycznej tangens otrzymamy:
.
To oczywiście oznacza, że kąt ma miarę , jako kąt wewnętrzny trójkąta prostokątnego . Ponieważ jednak trójkąt jest trójkątem równoramiennym, bo wysokości ścian bocznych są sobie równe, to ostatecznie kąty wewnętrzne tego trójkąta są równe odpowiednio:
oraz .
Ważną umiejętnością jest rozróżnianie w ostrosłupach kątów nachylenia krawędzi bocznych do płaszczyzny podstawy oraz kątów nachylenia ścian bocznych do płaszczyzny podstawy. Aby porównać ze sobą te dwa rodzaje kątów, rozpatrzmy następujący przykład.
Wyznaczymy cosinusy kątów, jakie tworzą krawędź boczna i ściana boczna z podstawą prawidłowego ostrosłupa pięciokątnego, którego ściany boczne są trójkątami równobocznymi.
Rozwiązanie:
Przyjmijmy następujące oznaczenia dla ostrosłupa:
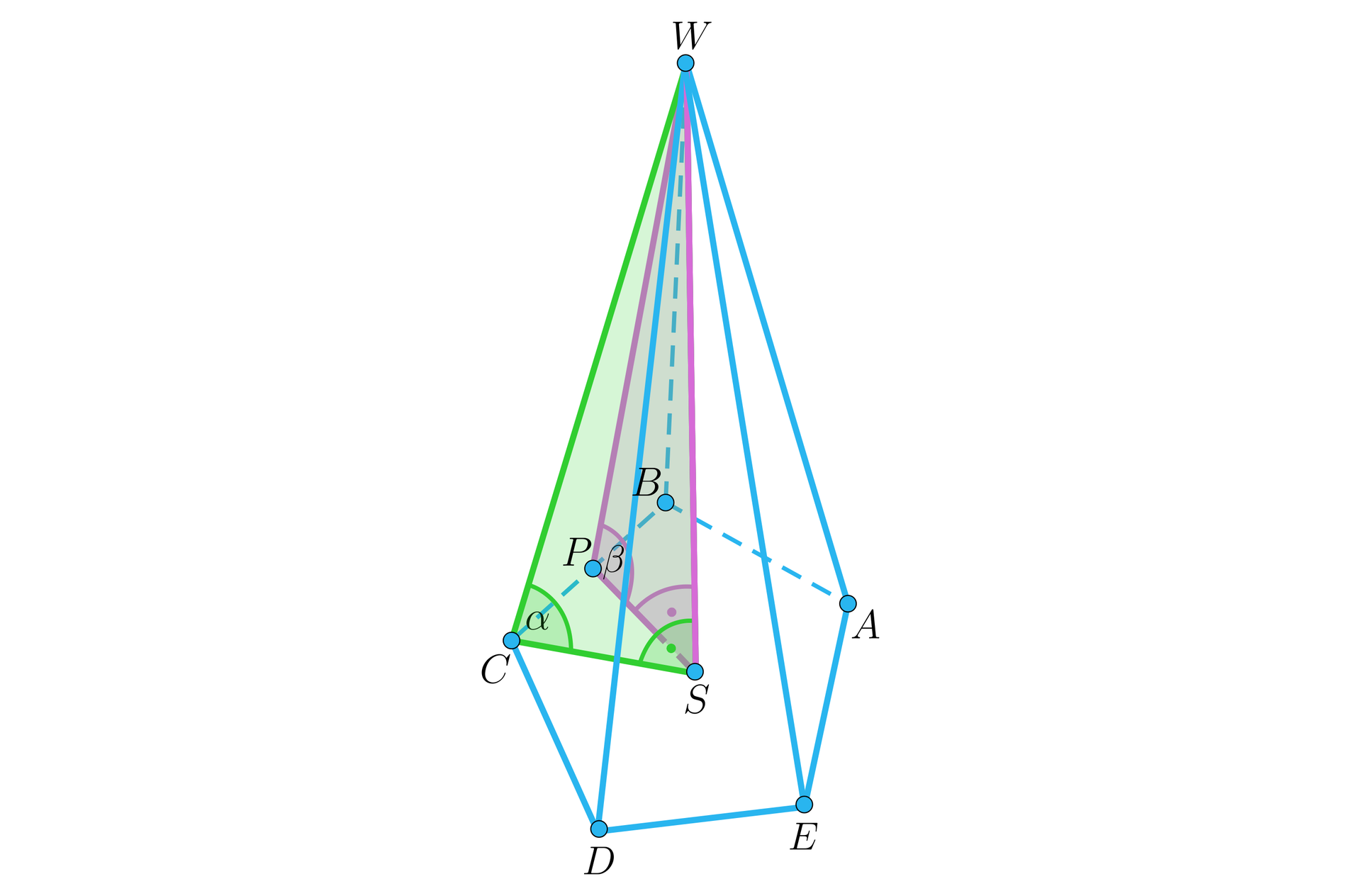
Mamy wyznaczyć miary dwóch kątów oznaczonych na rysunku symbolami i . Pierwszy kąt jest kątem między prostą a płaszczyznąkątem między prostą a płaszczyzną, drugi jest kątem między płaszczyznamikątem między płaszczyznami. Ponieważ wszystkie ściany boczne są trójkątami równobocznymi, to wszystkie krawędzie ostrosłupa są tej samej długości. Oznaczmy tę długość symbolem .
Rozważmy najpierw własności podstawy naszego ostrosłupa, czyli pięciokąta foremnego.

Skoro pięciokąt jest foremny, to jego kąt środkowykąt środkowy ma miarę . Pozwala to wyznaczyć długości odcinków oraz w zależności od przyjętej długości krawędzi .
Odcinek (promień okręgu wpisanego do pięciokąta) wyrażamy przez z trójkąta :
.
Jednocześnie ten sam trójkąt pozwala nam wyznaczyć odcinek (promień okręgu opisanego na pięciokącie):
Wykorzystując tablice trygonometryczne, możemy odszukać dokładne wartości funkcji oraz . Mamy zatem:
oraz
Ostatecznie wykorzystując w ostrosłupie trójkąt otrzymujemy cosinus kąta między krawędzią boczną a płaszczyzną podstawy ostrosłupa:
Analogicznie dla trójkąta wyznaczamy cosinus kąta między ścianą boczną a płaszczyzną podstawy ostrosłupa:
.
Oczywiście, jeżeli zamiast dokładnych wartości funkcji trygonometrycznych kąta wykorzystalibyśmy ich wartości przybliżone, to wartość merytoryczna naszego rozwiązania nie uległaby zmianie.
Zaznaczanie kątów w ostrosłupach prawidłowychostrosłupach prawidłowych jest dość powtarzalne. Po rozwiązaniu kilku zadań można zapamiętać, gdzie znajdują się rzuty najczęściej wykorzystywanych odcinków. Dlatego aby sprawdzić swoją umiejętność pracy z kątem między prostą a płaszczyzną w ostrosłupach, warto popracować z zadaniami, w których rozpatrywany ostrosłup nie jest prawidłowy.
Podstawą ostrosłupa jest kwadrat . Krawędź boczna tego ostrosłupa jest prostopadła do płaszczyzny podstawy. Najdłuższa i najkrótsza krawędź boczna tego ostrosłupa pozostają ze sobą w stosunku . Obliczymy sinusy kątów nachylenia krawędzi bocznych ostrosłupa do jego płaszczyzny podstawy.
Rozwiązanie:
Zacznijmy od rysunku:
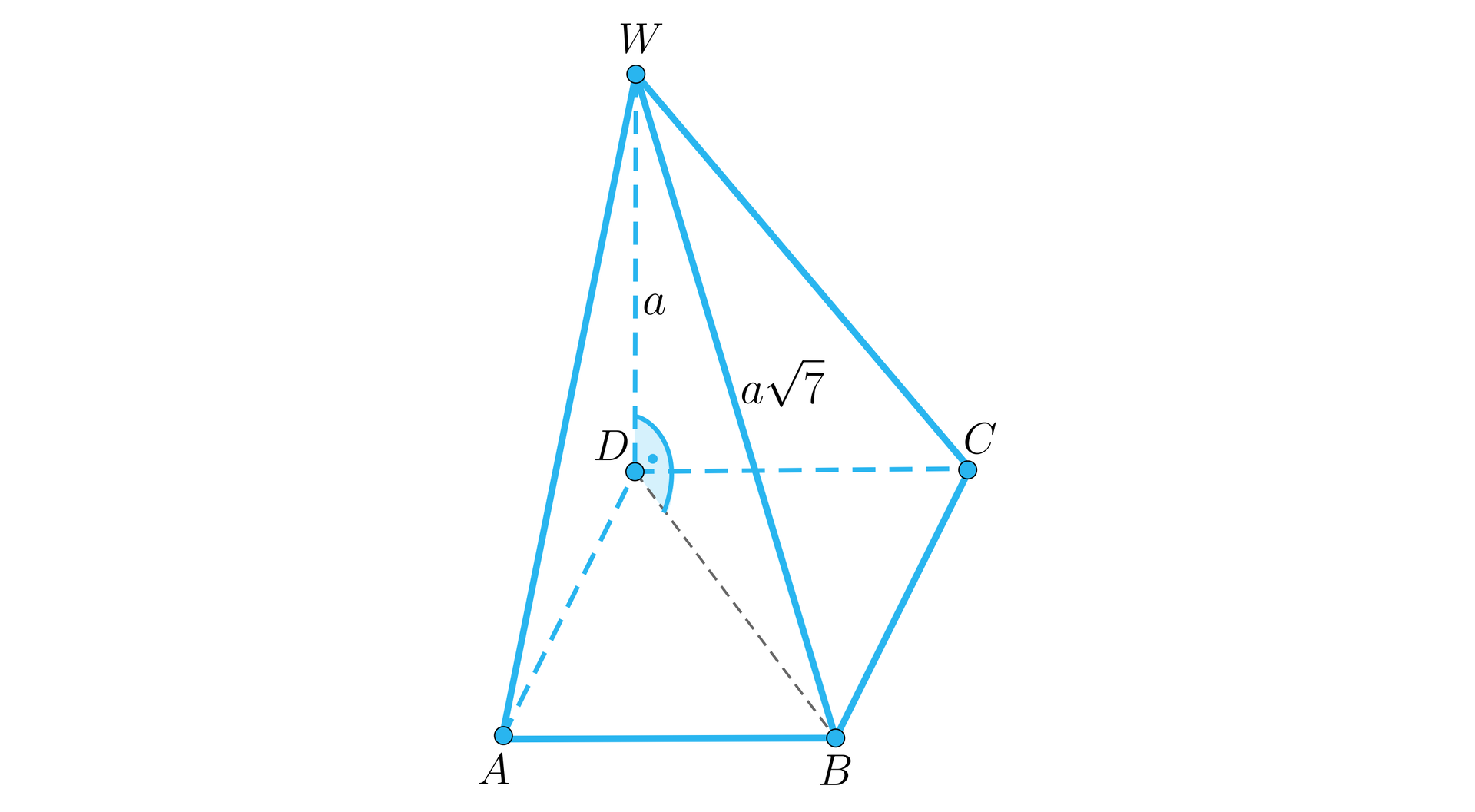
Przeanalizujemy najpierw kąty nachylenia poszczególnych krawędzi bocznych do płaszczyzny podstawy. Jeżeli krawędź jest prostopadła do podstawy, to pierwszy z poszukiwanych sinusów kątów to . Dla pozostałych krawędzi bocznych jeden ich koniec już należy do podstawy, zaś drugim końcem jest punkt . Rzutem prostokątnym tego punktu na płaszczyznę jest punkt . Konsekwentnie rzutem prostokątnym odcinka na podstawę jest odcinek , dla odcinka jest to odcinek i dla odcinka jest to odcinek .
Na rysunku sytuację możemy przedstawić następująco:
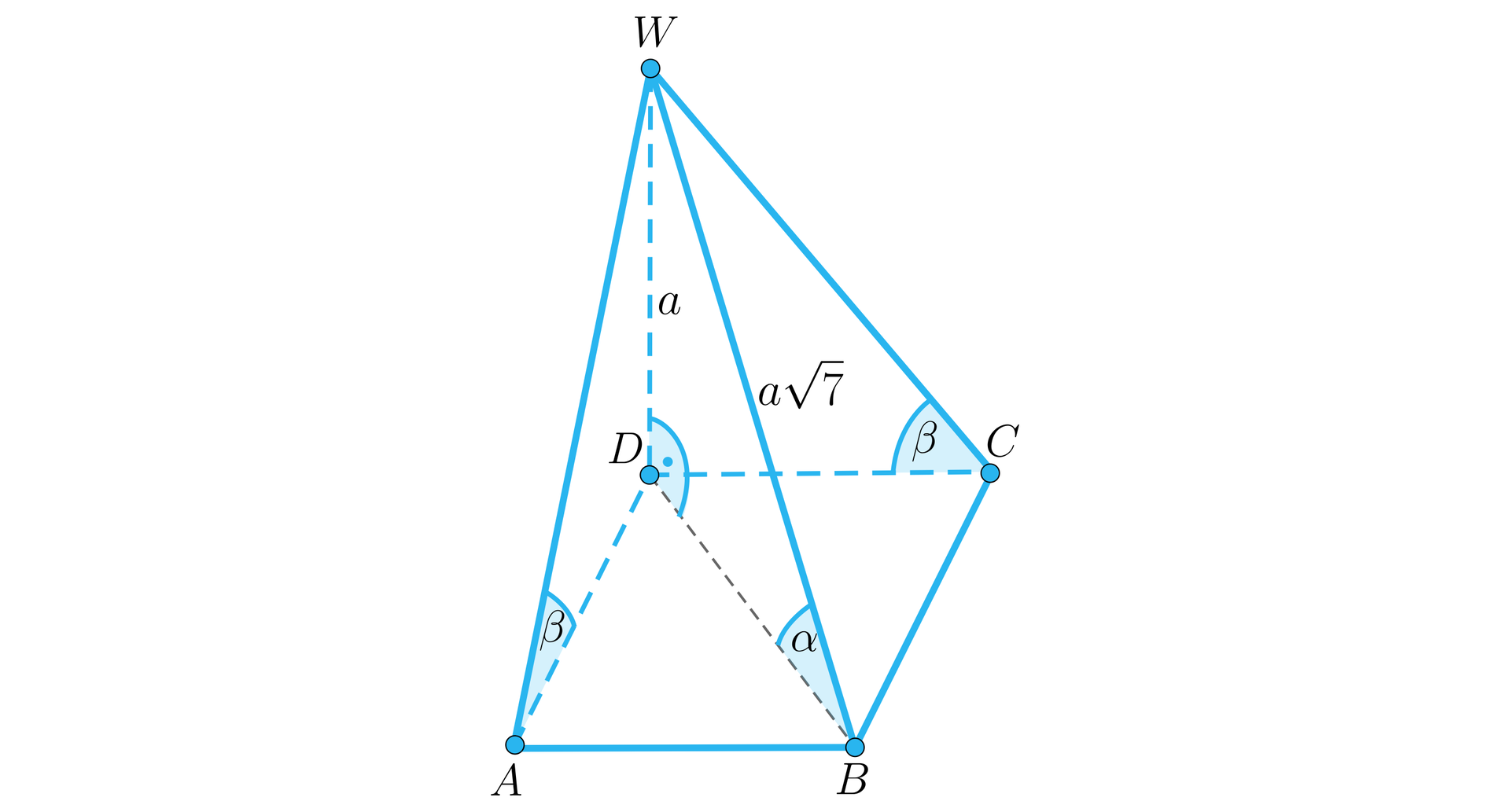
Musimy zatem obliczyć sinus kąta między krawędzią boczną a przekątną podstawy:
.
Analogicznie postępujemy obliczając sinus kąta nachylenia krawędzi oraz krawędzi do płaszczyzny podstawy:
.
Brakującą długość krawędzi bocznej wyznaczymy na mocy twierdzenia Pitagorasa stosowanego kolejno w trójkątach , oraz :
Możemy już obliczyć sinus kąta :
.
Rozwiązanie ostatniego przykładu wymagało nie tyle biegłości w zastosowaniu trygonometrii, co umiejętności poprawnego zastosowania definicji kąta między prostą a płaszczyzną. Warto zauważyć, że kąt nachylenia krawędzi bocznej do płaszczyzny podstawy pokrył się z kątem między krawędzią boczną a krawędzią podstawy, zaś kąt nachylenia krawędzi bocznej do płaszczyzny podstawy pokrył się z kątem między krawędzią boczną a przekątną podstawy ostrosłupa. Błędna interpretacja wspomnianej definicji doprowadziłaby do błędnego rozwiązania zadania. Należy zatem w każdym przypadku dobrze przemyśleć swoje decyzje, aby potem doprowadzić do prawidłowego rezultatu.
Na koniec jeszcze jeden aplet, na którym są widoczne różnego rodzaju kąty w ostrosłupach. Niech takie podsumowanie pozwoli na uporządkowanie poznanych wiadomości o kątach w ostrosłupach.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfBWskNyM
Słownik
kąt między prostą a jej rzutem prostopadłym na daną płaszczyznę
każda z dwóch części przestrzeni, na jakie dzielą ją dwie półpłaszczyzny, nazywane ścianami kąta dwuściennego, mające wspólną krawędź nazywaną krawędzią kąta dwuściennego, wraz z punktami każdej półpłaszczyzny
twierdzenie określające związek między kątem wewnętrznym trójkąta i bokami tego trójkąta:
w dowolnym trójkącie kwadrat długości jednego z boków jest równy sumie kwadratów długości pozostałych dwóch boków pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta między nimi zawartego
ostrosłup prosty, którego podstawa jest wielokątem foremnym
kąt, którego wierzchołkiem jest środek okręgu opisanego na tym wielokącie, a ramiona zawierają promienie tego okręgu poprowadzone do dwóch sąsiednich wierzchołków wielokąta