Przeczytaj
Zadania optymalizacyjne z jednej strony wymagają za każdym razem indywidualnego podejścia, z drugiej mają pewien powtarzający się schemat postępowania.
Uzależnienie wszystkich potrzebnych wymiarów od jednej zmiennej
Wyznaczenie funkcji opisującej badaną wielkość
Wyznaczenie dziedziny otrzymanej funkcji
Obliczenie pochodnej otrzymanej funkcji
Wyznaczenie miejsc zerowych pochodnej
Uzasadnienie maksimum/minimum funkcji
Obliczenie największej/najmniejszej wartości funkcji
Z blachy należy zrobić zbiornik w kształcie prostopadłościanu o objętości . Spód tego zbiornika jest kwadratem. Koszt blachy na wykonanie podłogi i pokrywy wynosi , natomiast koszt materiału na ściany boczne wynosi . Wyznaczymy wymiary zbiornika aby koszt budowy był jak najmniejszy.
Rozwiązanie:
Oznaczmy:
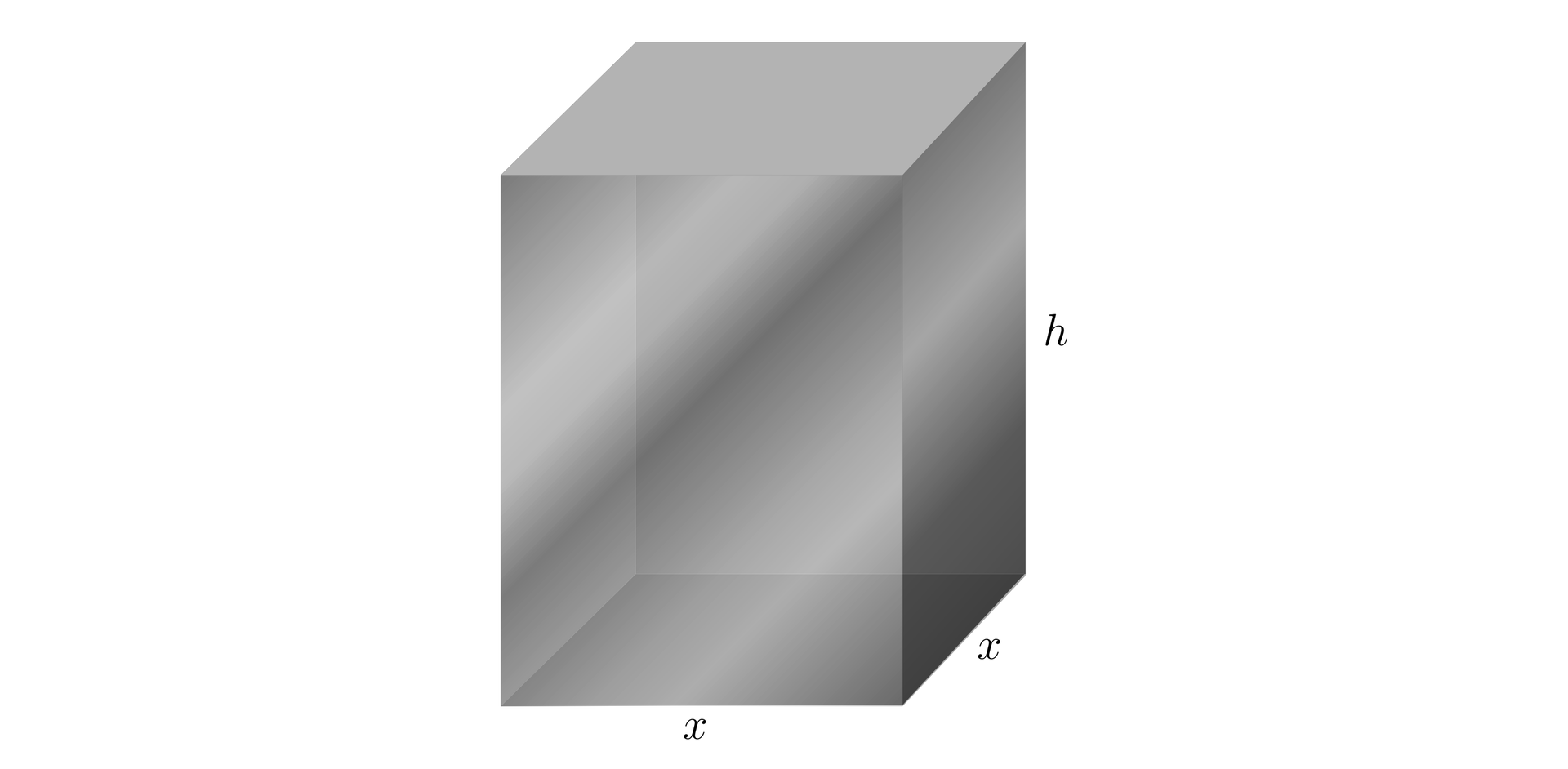
Objętość możemy zapisać . Podstawiając dane oraz wyznaczając wysokość otrzymujemy
Pole powierzchni całkowitej wynosi . Następnie utworzymy funkcję kosztu, z danych . Mamy zatem
Stąd otrzymujemy funkcję zmiennej opisującą koszt wykonania zbiornika w zależności od długości krawędzi podstawy.
Wyznaczymy dziedzinę, boki muszą być dodatnie
Wyznaczymy pochodną
Miejscem zerowej pochodnej jest . Możemy zaobserwować, że należy do dziedziny
Naszkicujemy wykres pochodnej w otoczeniu miejsca zerowego
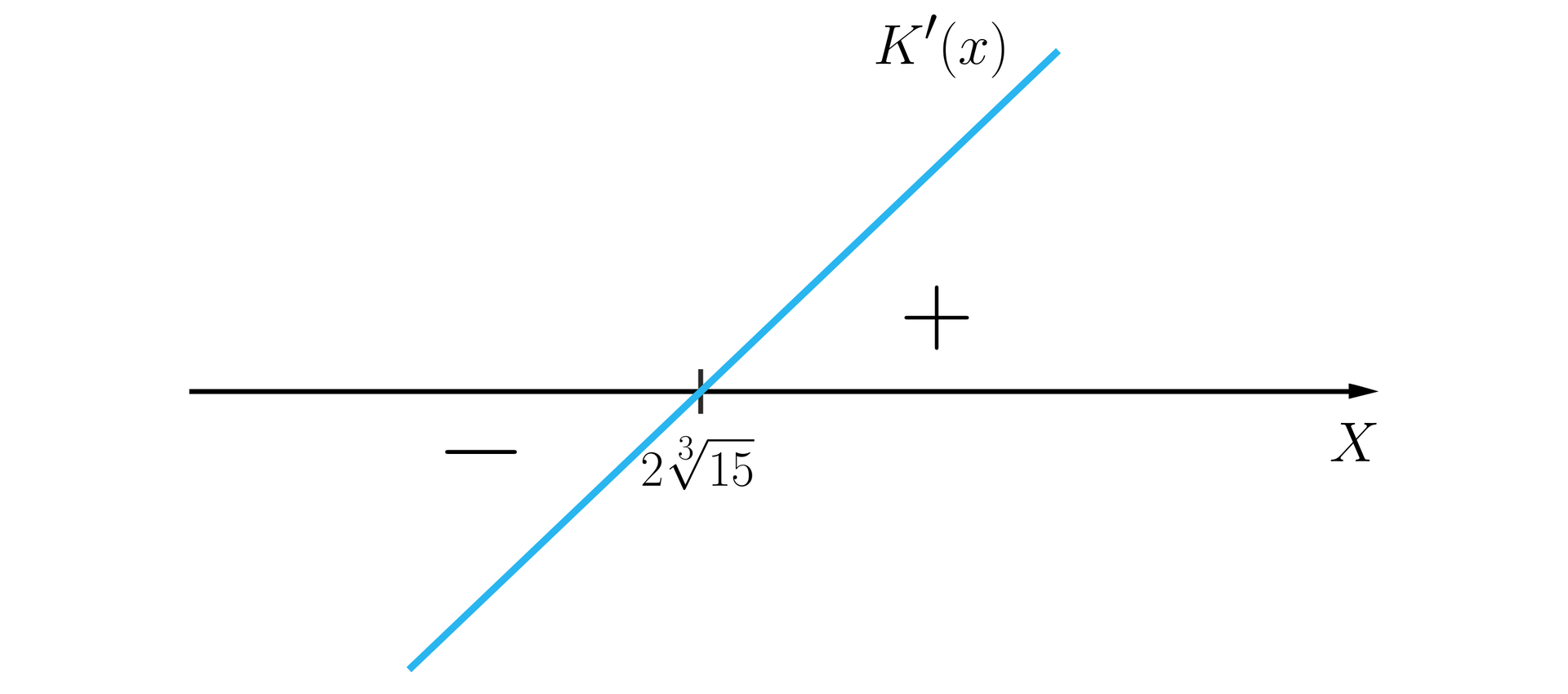
Wyznaczymy tabelę
MIN |
Funkcja osiąga minimum dla . Zatem koszt wykonania zbiornika będzie najmniejszy, gdy . Wówczas wysokość zbiornika wynosi .
Wymiary zbiornika to .
W galerii sztuki zawieszony jest obraz o wysokości , tak, że jego dolny brzeg znajduje się na wysokości oczu oglądającego tj. od podłogi (zobacz rysunek). Wyznaczymy w jakiej odległości oglądający powinien postawić aparat na podłodze, aby kąt widzenia obrazu był największy (pomiń wysokość aparatu).
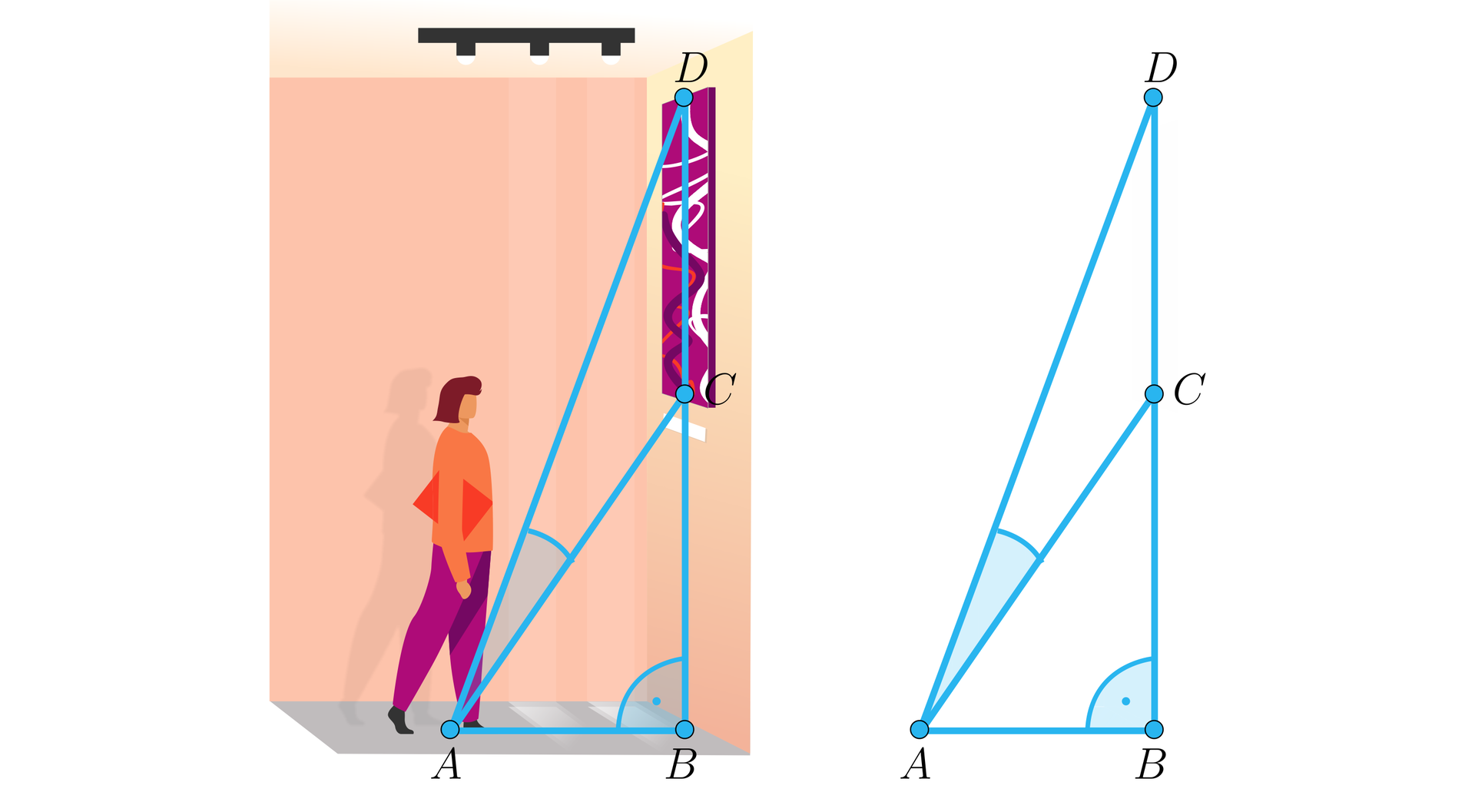
Rozwiązanie:
Przyjmijmy oznaczenia jak na rysunku.
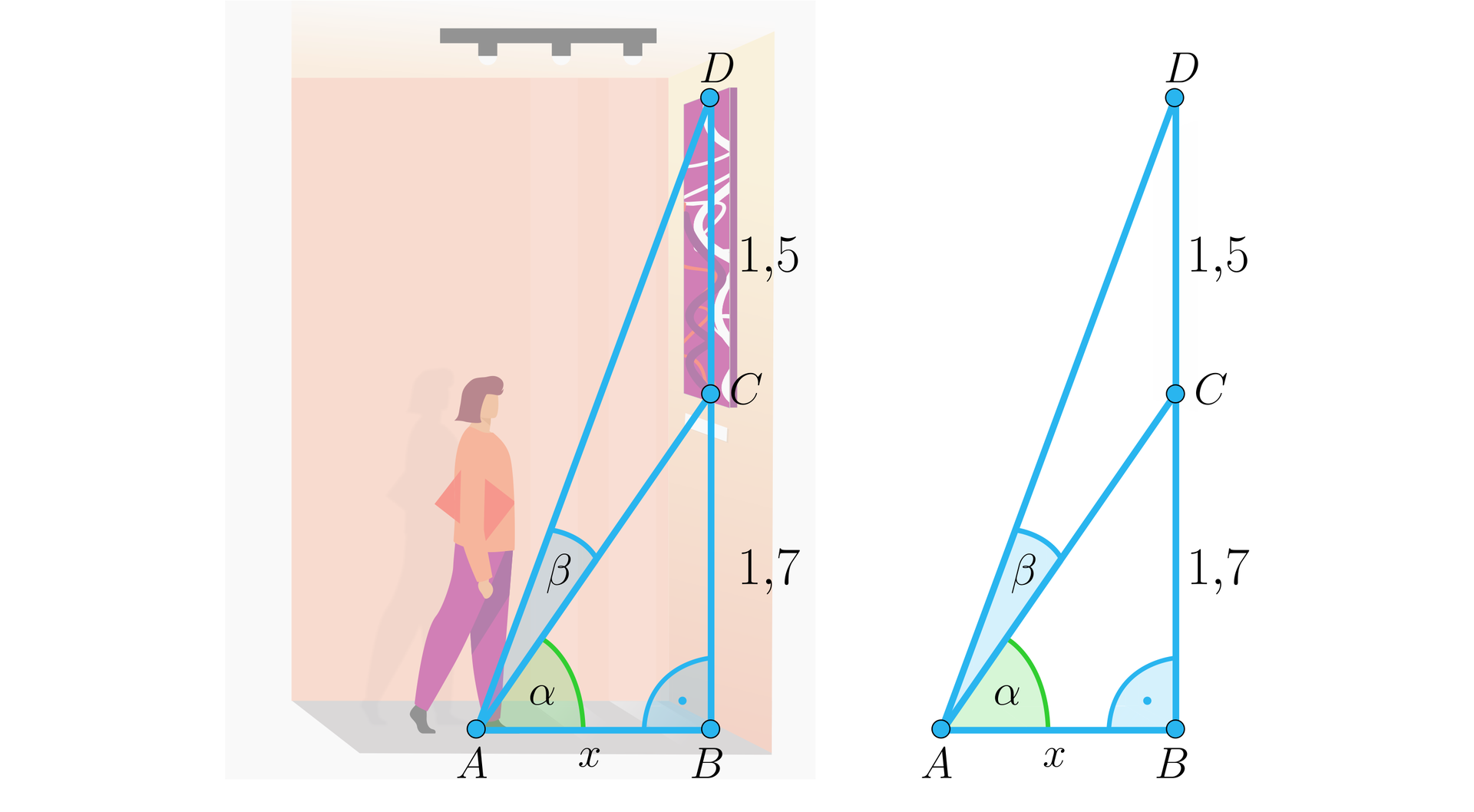
Zauważmy, że oraz .
Rozpisując wzór na tangens sumy kątówtangens sumy kątów mamy, że
, tj. .
Stąd
Wyznaczymy
Zauważmy, że dla kąta z przedziału funkcja tangens jest rosnąca. Dlatego szukając maksimum lokalnego funkcji możemy szukać maksimum lokalnego funkcji
Dziedziną jest zbiór
Wyznaczymy pochodną korzystając ze wzoru na iloraz pochodnych
Aby wyznaczyć miejsce zerowej pochodnej wystarczy licznik przyrównać do zera. Miejsca zerowe zaokrąglimy do dwóch miejsc po przecinku oraz . Pierwsze miejsce zerowe nie należy do dziedziny. Naszkicujemy wykres pochodnej.
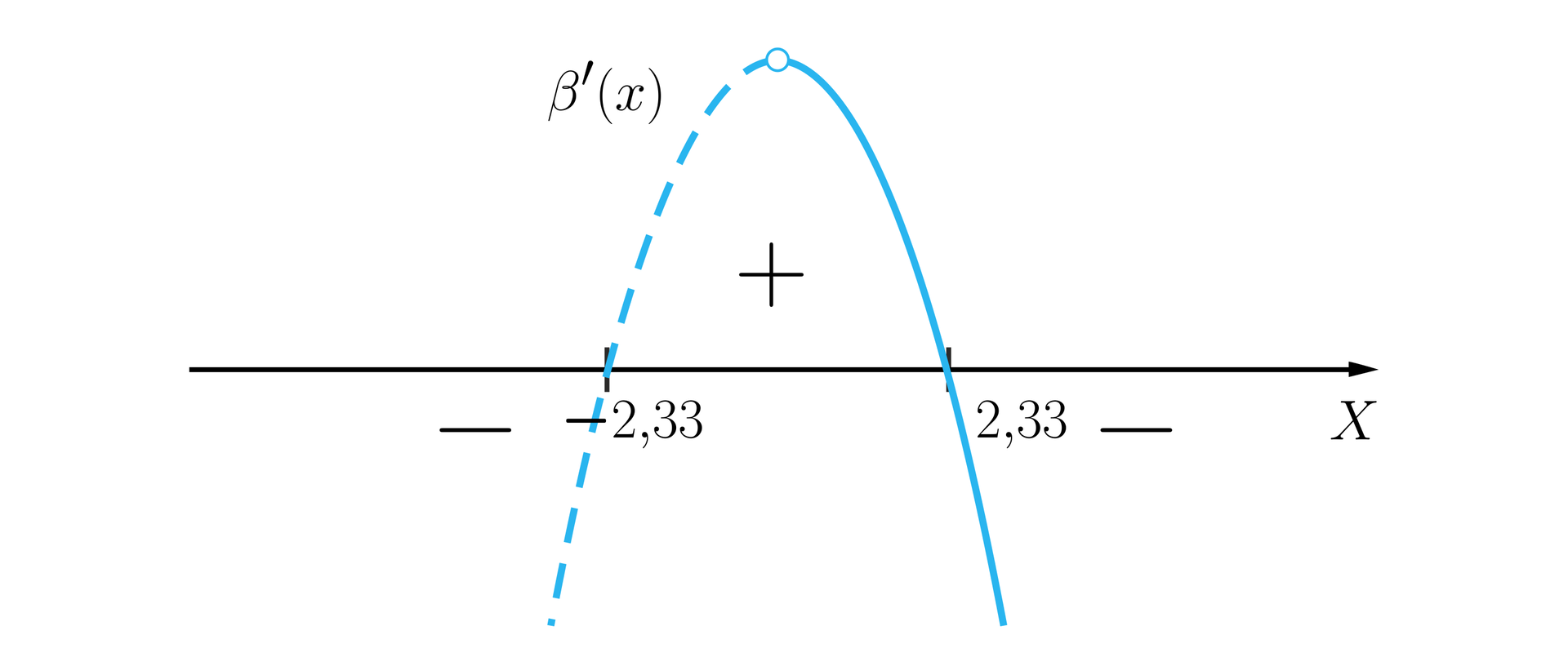
Stworzymy tabelę.
MAX |
Funkcja osiąga maksimum w . Oglądający powinien postawić aparat w odległości od ściany.
W zbiorniku znajdowało się litrów wody. Po odkręceniu zaworów, w ciągu pierwszej minuty do zbiornika napłynęło litrów wody, a w każdej następnej minucie o litry wody więcej niż w poprzedniej. Jednocześnie przez zawór odpływowy w ciągu każdej minuty wydostawało się litrów wody. Wyznaczymy w jakiej minucie było w zbiorniku najmniej wody.
Rozwiązanie:
Napływanie wody do zbiornika jest ciągiem arytmetycznym oznaczmy jako o pierwszym wyrazie i różnicy . Natomiast wypływanie wody ze zbiornika jest ciągiem arytmetycznym oznaczmy go jako o pierwszym wyrazie i różnicy .
Utworzymy nowy ciąg , taki, że . Ciąg jest ciągiem arytmetycznym o pierwszym wyrazie i różnicy .
Wyznaczymy sumę początkowych wyrazów ciągu sumę początkowych wyrazów ciągu . Skorzystamy ze wzoru
W zbiorniku było wcześniej litrów wody. Otrzymaliśmy w ten sposób funkcję zmiennej opisującą liczbę litrów wody w zbiorniku w czasie
Oczywiście badając ciągi myślimy o liczbach naturalnych. Jednak rozszerzmy dziedzinę rozważanej funkcji do wszystkich liczb rzeczywistych dodatnich, tj.
Wyznaczymy pochodną
Miejscem zerowym pochodnej jest , oczywiście należy do dziedziny.
Naszkicujemy wykres pochodnej w otoczeniu miejsca zerowego
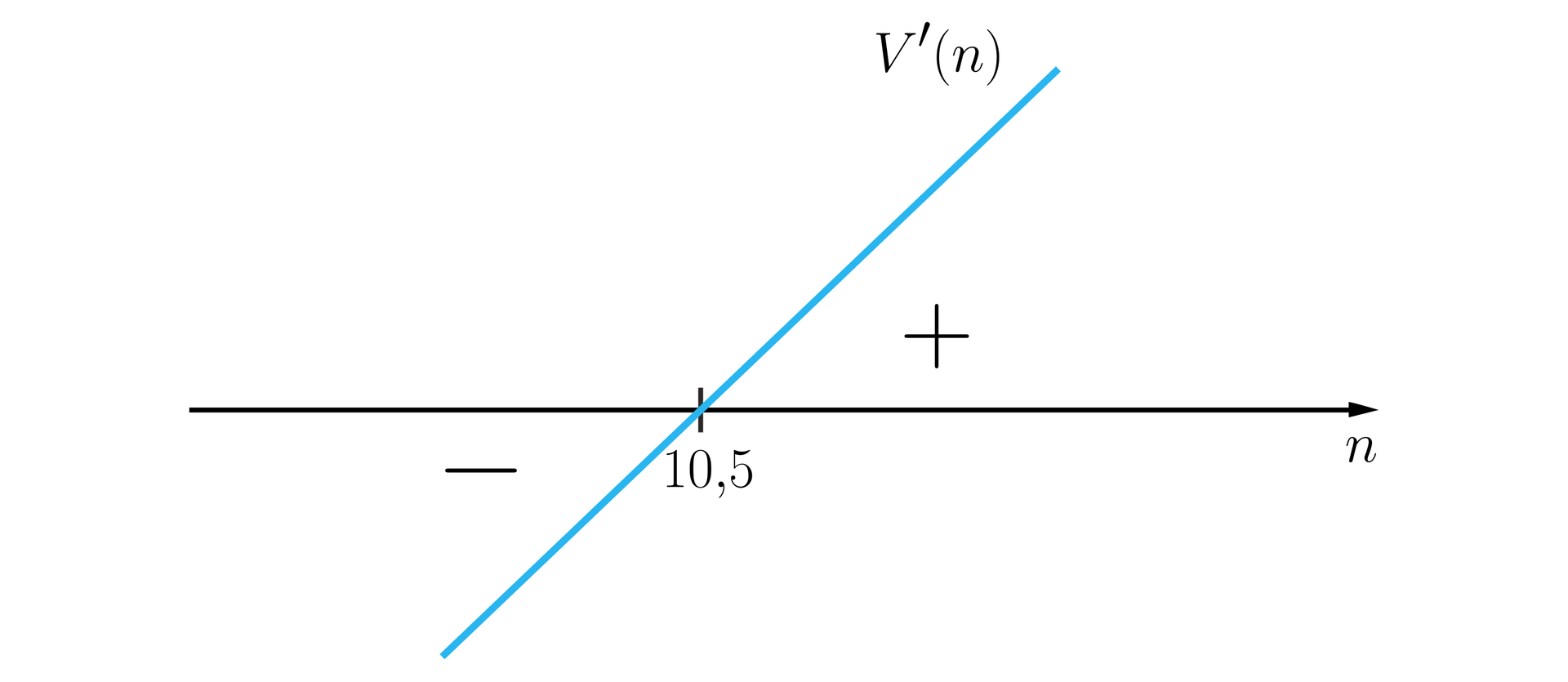
Wyznaczymy tabelę
MIN |
Funkcja osiąga minimum dla . Oznacza to, że najwięcej wody w zbiorniku mieliśmy w jedenastej minucie.
Sprzedawca kupuje w hurtowni telefony komórkowe płacąc za sztukę. Sprzedaje telefonów w cenie za sztukę. Pewnego razu zaobserwował, że obniżka ceny o każde kolejne zwiększa o liczbę sprzedanych telefonów. Wyznaczymy jaką cenę powinien ustalić sprzedawca, aby jego zysk był największy.
Rozwiązanie:
Oznaczmy:
– obniżka ceny o pięć złotych, razy,
– liczba sprzedanych telefonów po obniżce,
– zysk po obniżce.
Tworzymy funkcję zmiennej opisującą zysk uzyskany po -tej obniżce
Wyznaczymy dziedzinę funkcji pamiętając, że liczba sprzedanych telefonów to liczba naturalna oraz że sprzedawca nie sprzeda telefonu za mniej niż zł.
Wyznaczymy pochodną korzystając ze wzoru na pochodną iloczynupochodną iloczynu
Upraszczając
Miejscem zerowym pochodnej jest . Możemy zaobserwować, że należy do dziedziny. Naszkicujemy wykres funkcji pochodnej
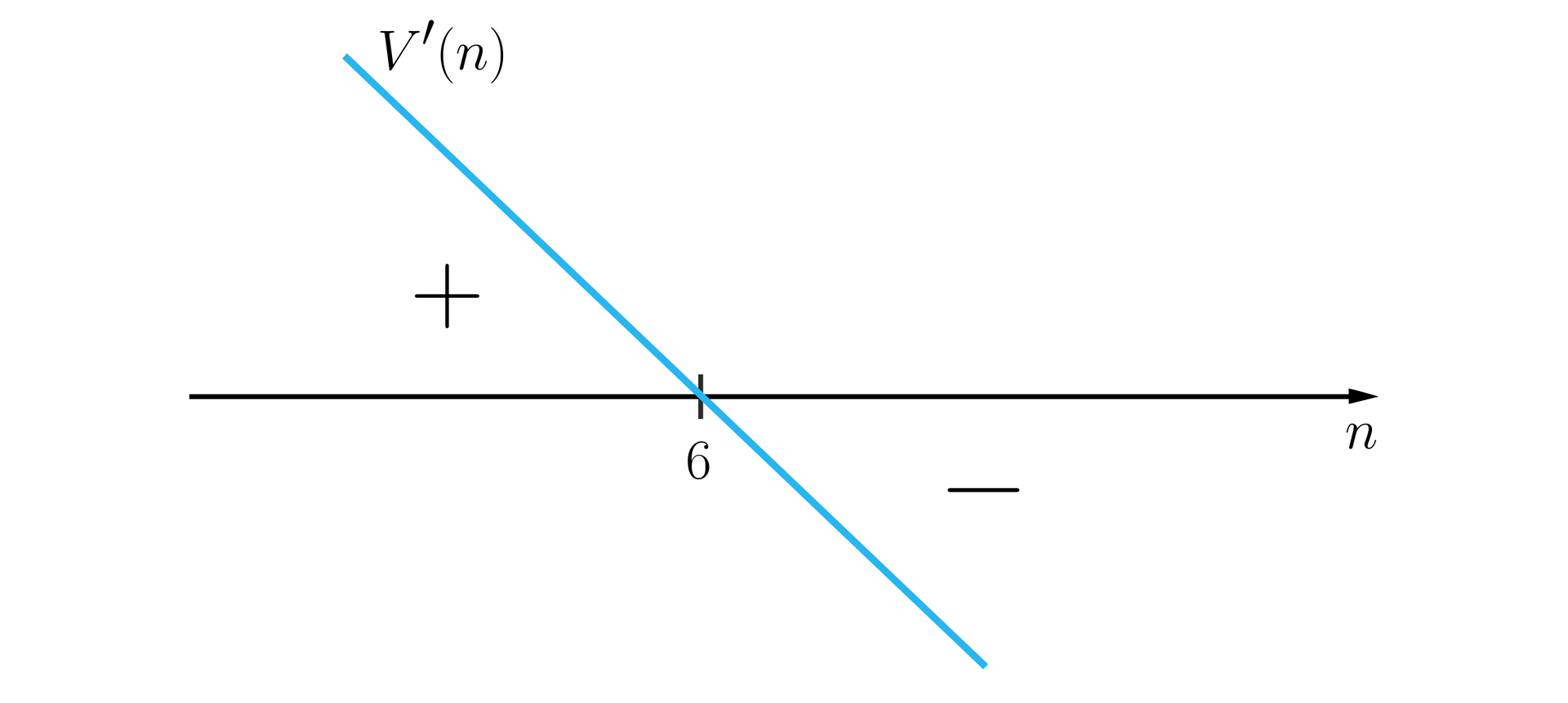
Słownik
wyraża się wzorem
dla wszystkich , oprócz tych dla których , lub jest nieokreślony
możemy ją wyliczyć ze wzoru
możemy wyznaczyć ze wzoru
lub