Dane jest równanie $\frac{-3}{x-1}-2=m$ z niewiadomą $x$ i parametrem $m$. Wyznaczymy wartość parametru $m$, dla którego równanie:

a) ma rozwiązanie,
b) ma rozwiązanie będące liczbą dodatnią.

Rozwiązanie

Sporządzamy wykres funkcji $s\left(x\right)=\frac{-3}{x-1}-2$.

Wykres funkcji przedstawia rysunek:

RPxEBLe13vS7k

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do 7, oraz pionową osią y od minus 6 do pięć. W płaszczyźnie układu zaznaczono dwie krzywe będące wykresem funkcji $y=s\left(x\right)$. Krzywe mają kształt hiperboli, ich pozioma asymptota to $y=-2$, z kolei pionowa asymptota ma równanie $x=1$. W układzie zaznaczony został również obszar znajdujący się po prawej stronie od osi y, pionowa linia wyznaczająca ten obszar została namalowana linia przerywaną.

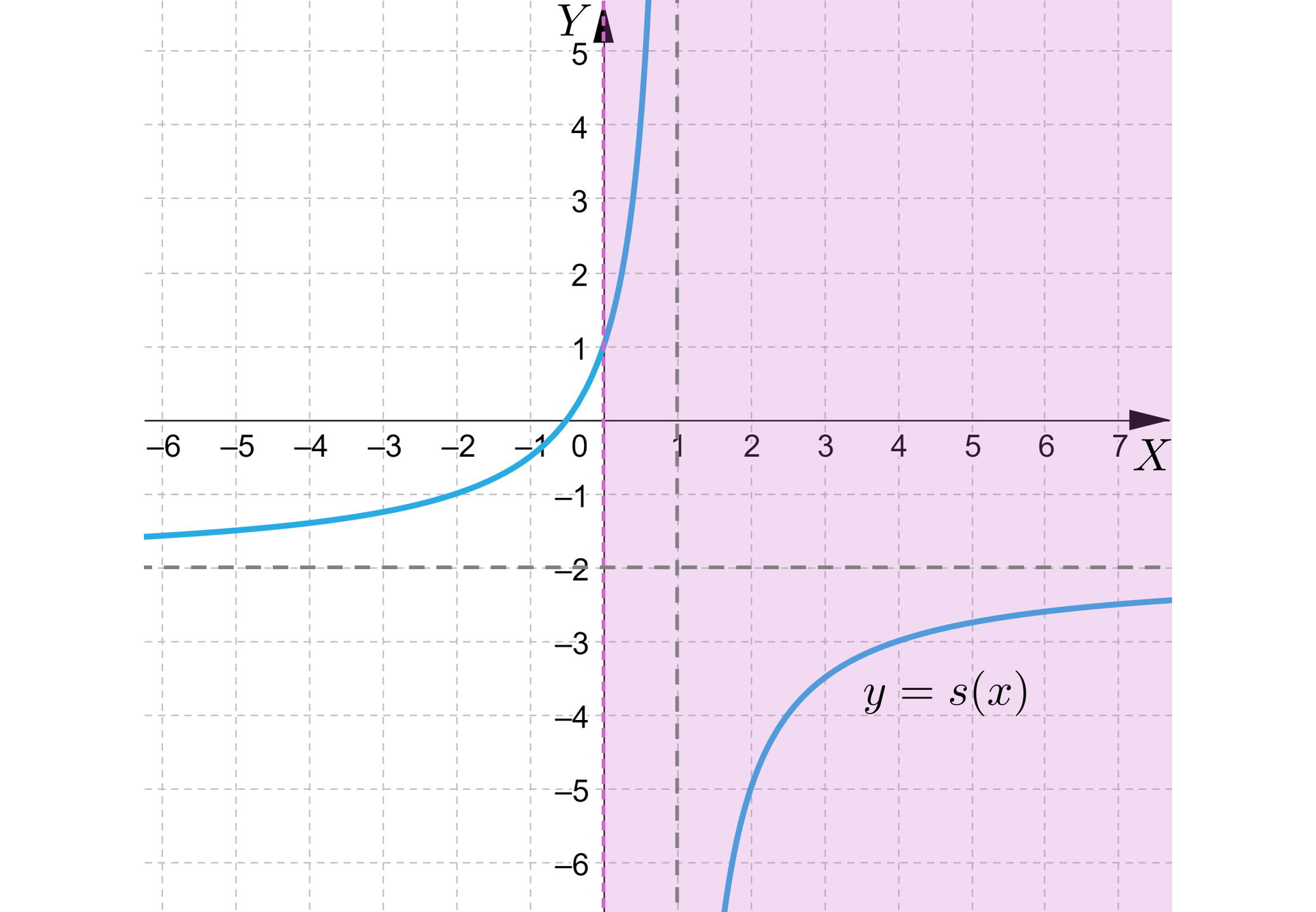
Prawą stronę równania przedstawiamy za pomocą wykresu   funkcji stałej $g\left(x\right)=m$.  Wykresem tej funkcji jest prosta równoległa do osi $X$. Równanie będzie miało rozwiązanie, gdy wykresy  funkcji $s\left(x\right)$ oraz $g\left(x\right)$ będą miały punkt wspólny. Zauważmy, że tylko dla jednego położenia wykresu  funkcji $g\left(x\right)$ tak się nie stanie. Taka sytuacja jest dla $g\left(x\right)=-2$.

Odpowiedź

a) Równanie ma rozwiązanie dla $m\in \mathrm{ℝ}\setminus \left\{-2\right\}$.

b) Równanie ma rozwiązanie dodatnie dla $m\in \left(-\infty ;-2\right)\cup \left(1;\infty \right)$ - odczytujemy z wykresu te wartości funkcji $g\left(x\right)$, dla których oba wykresy  funkcji będą miały punkt wspólny po prawej stronie osi $Y$, czyli dla $x>0$. Innymi słowy odczytujemy, dla jakiego $y$ wykres funkcji znajduje się w kolorowym obszarze.

Dane jest równanie $\frac{-2x-2}{x+2}=m+5$ z niewiadomą $x$ i parametrem $m$. Wyznaczymy wartość parametru $m$, dla którego równanie ma rozwiązanie będące liczbą mniejszą od $\left(-3\right)$.

Rozwiązanie

Sporządzamy wykres funkcji: $w\left(x\right)=\frac{-2x-2}{x+2}$.

W tym celu przekształcimy wzór funkcji do postaci kanonicznej:

$w\left(x\right)=\frac{-2x-2}{x+2}=\frac{-2\left(x+2\right)+2}{x+2}=-2+\frac{2}{x+2}$.

Wykres funkcji przedstawia rysunek:

R1Mw914z5b3Nr

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 8 do 4, oraz pionową osią y od minus 6 do pięć. W płaszczyźnie układu zaznaczono dwie krzywe będące wykresem funkcji $y=w\left(x\right)$. Wykres ma kształt hiperboli, jego pozioma asymptota to $y=-2$, z kolei pionowa asymptota ma równanie $x=-2$. W układzie zaznaczone zostały również dwa obszary, pierwszy z nich znajduje się po lewej stronie od pionowej prostej namalowanej linią przerywaną o równaniu $x=-3$. Drugi obszar zawiera się pomiędzy poziomymi prostymi narysowanymi liniami przerywanymi o równaniach $y=-2$ oraz $y=-4$.

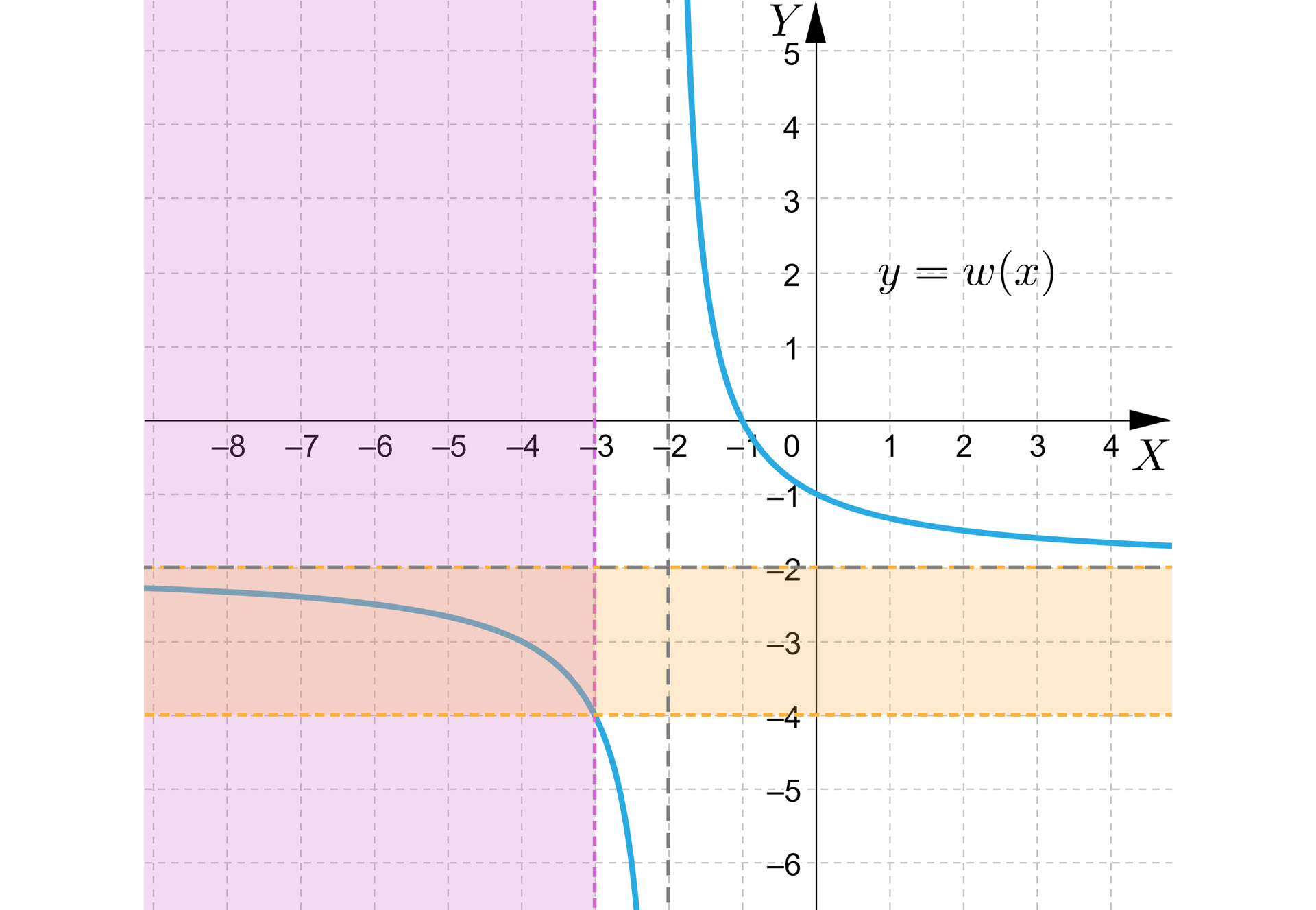
Prawą  stronę równania obrazujemy za pomocą wykresu funkcji   $g\left(x\right)=m+5$. Wykresem tej funkcji jest prosta równoległa do osi $X$. Równanie będzie miało rozwiązanie mniejsze od $\left(-3\right)$, gdy wykresy funkcji $w\left(x\right)$ oraz $g\left(x\right)$ będą miały punkt wspólny w obszarze fioletowym. Zauważmy, że wtedy wartości funkcji $g\left(x\right)$ muszą być większe od $\left(-4\right)$ i mniejsze od $\left(-2\right)$ - obszar pomarańczowy na rysunku:

czyli $-4<m+5<-2$,

zatem $-9<m<-7$.

Ustalimy liczbę rozwiązań równania $\frac{2\left|x\right|-3}{\left|x\right|+3}=3-m^2$ w zależności od parametru $m$.

Rozwiązanie

Sporządzamy wykres funkcji $k\left(x\right)=\frac{2\left|x\right|-3}{\left|x\right|+3}$.

W tym celu przekształcamy wzór  funkcji do postaci kanonicznej:

$k\left(x\right)=\frac{2\left|x\right|-3}{\left|x\right|+3}=\frac{2\left(\left|x\right|+3\right)-9}{\left|x\right|+3}=2-\frac{9}{\left|x\right|+3}$.

Wykres funkcji przedstawia rysunek:

R8HjiFzDnoNqA

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do 6, oraz pionową osią y od minus 2 do pięć. W płaszczyźnie układu zaznaczono dwie krzywe będące wykresem funkcji $y=k\left(x\right)$. Pierwsza pojawia się na płaszczyźnie w drugiej ćwiartce układu współrzędnych przechodzi przez punkt o współrzędnych nawias minus sześć średnik jeden zamknięcie nawiasu i biegnie po łuku do punktu nawias zero średnik minus jeden. Druga krzywa jest odbiciem lustrzanym pierwszej, rozpoczyna się w punkcie nawias zero średnik minus jeden i biegnie po łuku przez punkt nawias sześć średnik jeden zamknięcie nawiasu i wychodzi poza płaszczyznę układu w pierwszej ćwiartce układu współrzędnych. W układzie zaznaczony został przedział znajdujący się pomiędzy poziomymi prostymi narysowanymi liniami przerywanymi o równaniach $y=2$ i $y=-1$.

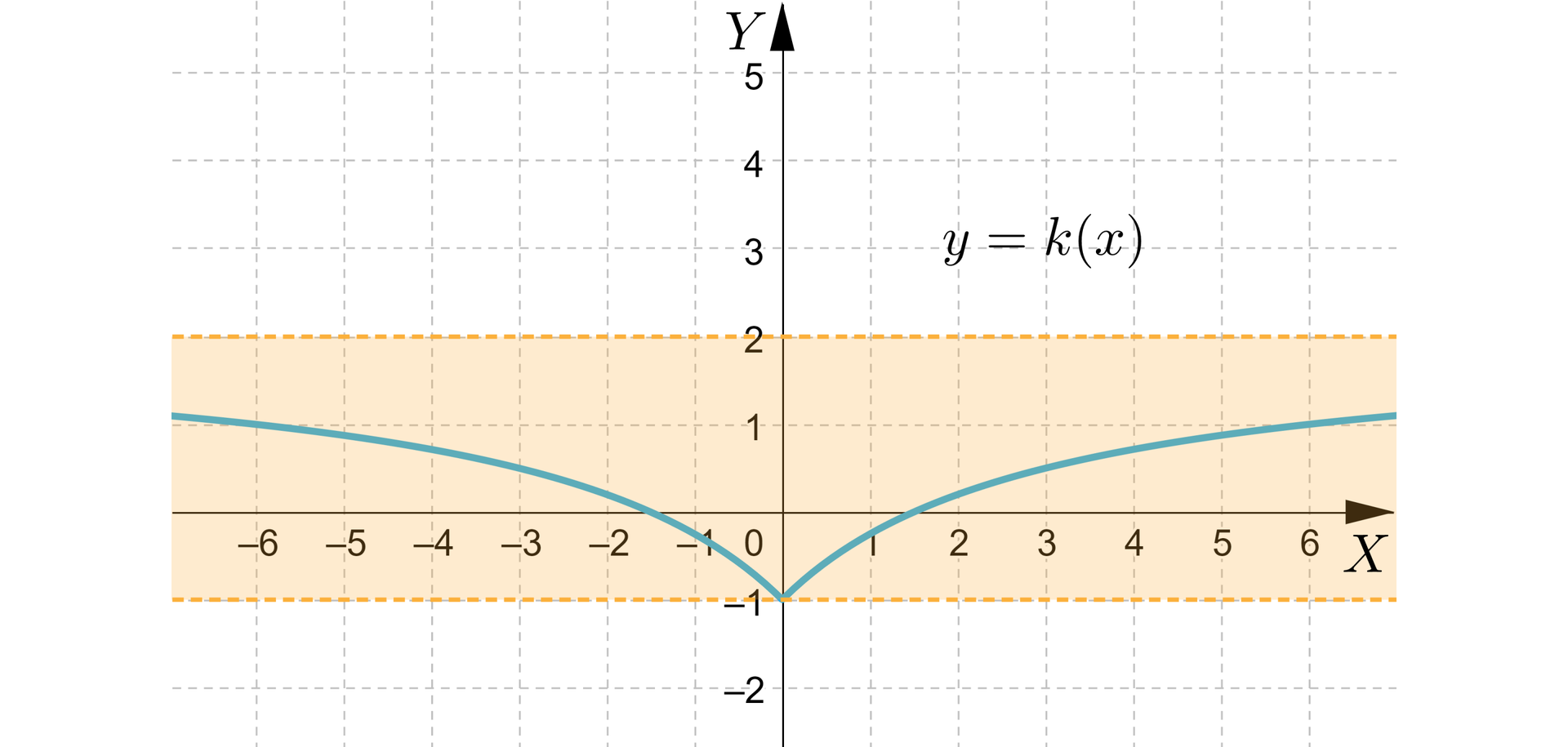
Prawą stronę równania  zobrazujemy za pomocą wykresu funkcji   $g\left(x\right)=3-m^2$.  Wykresem tej funkcji jest prosta równoległa do osi $X$. Równanie będzie miało rozwiązanie, gdy wykresy  funkcji $k\left(x\right)$ oraz $g\left(x\right)$ będą miały punkt wspólny.

Zauważmy, że jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w białym obszarze, to nie ma punktu wspólnego z wykresem funkcji $k\left(x\right)$, czyli równanie nie ma rozwiązań.

Jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w pomarańczowym obszarze, to ma dwa punkty wspólne z wykresem funkcji $k\left(x\right)$, czyli równanie ma dwa rozwiązania.

Dla $g\left(x\right)=-1$ wykresy funkcji mają jeden punkt wspólny, czyli równanie ma jedno rozwiązanie.

Odpowiedź

Równanie ma:

• 0 rozwiązań dla $3-m^2<-1$ lub $3-m^2\ge 2$,

  czyli $4-m^2<0$ lub $1-m^2\ge 0$,

  zatem $m\in \left(-\infty ;-2\right)\cup ⟨-1;1⟩\cup \left(2;\infty \right)$;

• 1 rozwiązanie dla $3-m^2=-1$,

  czyli $4-m^2=0$,

  zatem dla $m\in \left\{-2;2\right\}$;

• 2 rozwiązania dla $3-m^2>-1$ i $3-m^2<2$,

  czyli $4-m^2>0$ i $1-m^2<0$,

  zatem $m\in \left(-2;-1\right)\cup \left(1;2\right)$.

Ustalimy liczbę rozwiązań równania $\left|\frac{x-2}{x+2}\right|=m$ w zależności od parametru $m$.

Rozwiązanie

Sporządzamy wykres funkcji $f\left(x\right)=\left|\frac{x-2}{x+2}\right|$.

W tym celu przekształcamy wzór funkcji do postaci kanonicznej:

$f\left(x\right)=\left|\frac{x-2}{x+2}\right|=\left|\frac{x+2-4}{x+2}\right|=\left|1-\frac{4}{x+2}\right|$.

Wykres funkcji przedstawia rysunek:

RIIhmmuJ2f2RQ

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 7 do 5, oraz pionową osią y od minus 2 do pięć. W płaszczyźnie układu zaznaczono dwie krzywe będące wykresem funkcji $y=f\left(x\right)$. Pierwsza krzywa ma kształt hiperboli, jej pozioma asymptota to $y=-2$, z kolei pionowa asymptota ma równanie $x=1$. Druga krzywa składa się z dwóch części, pionowa część biegnie po łuku wzdłuż pionowej asymptoty, przecina oś y  w punkcie nawias zero średnik jeden zamknięcie nawiasu i biegnie do punktu nawias dwa średnik zero zamknięcie nawiasu. Stąd druga część krzywej biegnie po łuku wzdłuż poziomej asymptty i wychodzi poza płaszczyznę układu. W układzie zaznaczone zostały również dwa obszary, pierwszy z nich znajduje się powyżej poziomej prostej namalowanej linią przerywaną o równaniu $x=0$. Drugi obszar zawiera się poniżej tej prostej, z tym że tym razem została ona zaznaczona linią ciągłą.

Prawą stronę  równania  zobrazujemy za pomocą wykresu  funkcji  $g\left(x\right)=m$.   Wykresem tej funkcji jest prosta równoległa do osi $X$. Równanie będzie miało rozwiązanie, gdy  wykresy funkcji $f\left(x\right)$ oraz $g\left(x\right)$ będą miały punkt wspólny.

Zauważmy, że jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w fioletowym obszarze, to nie ma punktu wspólnego z wykresem funkcji $f\left(x\right)$, czyli równanie nie ma rozwiązań.

Jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w pomarańczowym obszarze (ale oprócz 0 i 1), to ma dwa punkty wspólne z wykresem funkcji $f\left(x\right)$, czyli równanie ma dwa rozwiązania.

Dla $g\left(x\right)=0$ i $g\left(x\right)=1$ wykresy funkcji mają jeden punkt wspólny, czyli równanie ma jedno rozwiązanie.

Odpowiedź

Równanie ma:

• 0 rozwiązań dla $m<0$;

• 1 rozwiązanie dla $m=0$ lub $m=1$;

• 2 rozwiązania dla $m\in \left(0;1\right)\cup \left(1;\infty \right)$.

Ustalimy liczbę rozwiązań równania $\left|\frac{-3\left|x\right|+2}{\left|x\right|-1}\right|=m$ w zależności od parametru $m$.

Rozwiązanie

Sporządzamy wykres funkcji $q\left(x\right)=\left|\frac{-3\left|x\right|+2}{\left|x\right|-1}\right|$.

W tym celu przekształcamy wzór  funkcji do postaci kanonicznej:

$q\left(x\right)=\left|\frac{-3\left|x\right|+2}{\left|x\right|-1}\right|=\left|\frac{-3\left(\left|x\right|-1\right)-1}{\left|x\right|-1}\right|=\left|-3-\frac{1}{\left|x\right|-1}\right|$.

Wykres funkcji przedstawia rysunek:

R4TPvbbNdI8nm

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do 6, oraz pionową osią y od minus 2 do siedem. W płaszczyźnie układu zaznaczono wykres funkcji $y=q\left(x\right)$, składa się on z trzech krzywych. Pierwsza krzywa ma kształt hiperboli o asymptotach: pionowa $x=-1$ i pozioma $y=3$. Druga krzywa składa się z czterech części: najpierw biegnie po łuku po prawej stronie pionowej asymptoty o równaniu $x=-1$ aż do punktu leżącego na osi x pomiędzy wartością minus jeden i zero, z tego punktu wykres biegnie po łuku do punktu nawias zero średnik dwa zamknięcie nawiasu, następnie biegnie znów po łuku do punktu znajdującego się na osi x pomiędzy wartościami zero i jeden, stąd ostatnia część biegnie po łuku wzdłuż pionowej asymptoty o równaniu $x=1$. Trzecia krzywa ma kształt hiperboli, której pionowa asymptota ma równanie $x=1$, a pozioma asymptota ma równanie $y=3$. W układzie zaznaczono również dwa obszary pierwszy z nich zawiera się pomiędzy dwiema poziomymi prostymi namalowanymi liniami przerywanymi o równaniach: $y=2$ oraz $y=3$. Drugi obszar składa się z dwóch fragmentów, pierwszy z nich znajduje się pomiędzy prostymi zaznaczonymi liniami przerywanymi o równaniach $y=0$ oraz $y=2$, a drugi fragment znajduje się powyżej prostej zaznaczonej linią przerywaną o równaniu $y=3$.

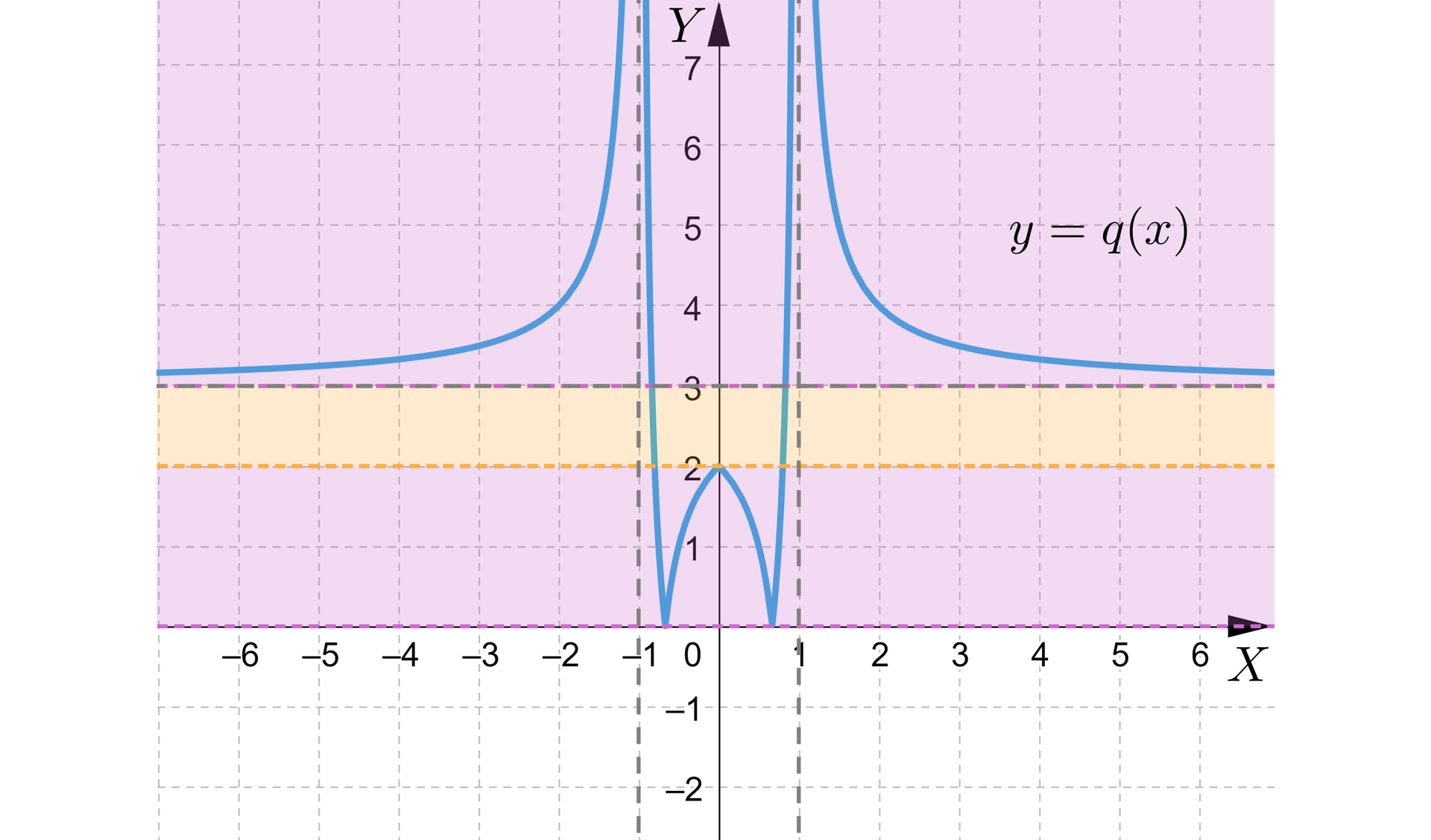
Prawą stronę równania obrazujemy za pomocą  funkcji stałej $g\left(x\right)=m$.   Wykresem tej funkcji jest prosta równoległa do osi $X$. Równanie będzie miało rozwiązanie, gdy wykresy funkcji $q\left(x\right)$ oraz $g\left(x\right)$ będą miały punkt wspólny.

Zauważmy, że jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w białym obszarze, to nie ma punktu wspólnego z wykresem funkcji $q\left(x\right)$, czyli równanie nie ma rozwiązań.

Jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w fioletowym obszarze, to ma cztery punkty wspólne z wykresem funkcji $q\left(x\right)$, czyli równanie ma cztery rozwiązania.

Jeśli wykres funkcji stałej $g\left(x\right)$ znajduje się w pomarańczowym obszarze lub na fioletowej lini, to ma dwa punkty wspólne z wykresem funkcji $q\left(x\right)$, czyli równanie ma dwa rozwiązania.

Dla $g\left(x\right)=2$ i wykresy funkcji mają trzy punkty wspólne, czyli równanie ma trzy rozwiązanie.

Odpowiedź

Równanie ma:

• 0 rozwiązań dla $m<0$;

• 2 rozwiązania dla $m\in \left\{0\right\}\cup \left(2;3\right.⟩$;

• 3 rozwiązania dla $m=2$;

• 4 rozwiązania dla $m\in \left(0;2\right)\cup \left(3;\infty \right)$.

funkcja, która jest ilorazem dwóch wielomianów

takie przekształcenie równania, w wyniku którego powstaje równanie o takim samym zbiorze rozwiązań

wyrażenie algebraiczne będące sumą jednomianów