Przeczytaj

Prostą, która ma dwa punkty wspólne z okręgiemokrąg o środku O i promieniu rokręgiem nazywamy sieczną okręgu.

Odcinek $A$ $B$ siecznej, ograniczony punktami przecięcia z okręgiem, nazywamy cięciwą okręgucięciwa okręgucięciwą okręgu.

R16lT1vaNRh7S

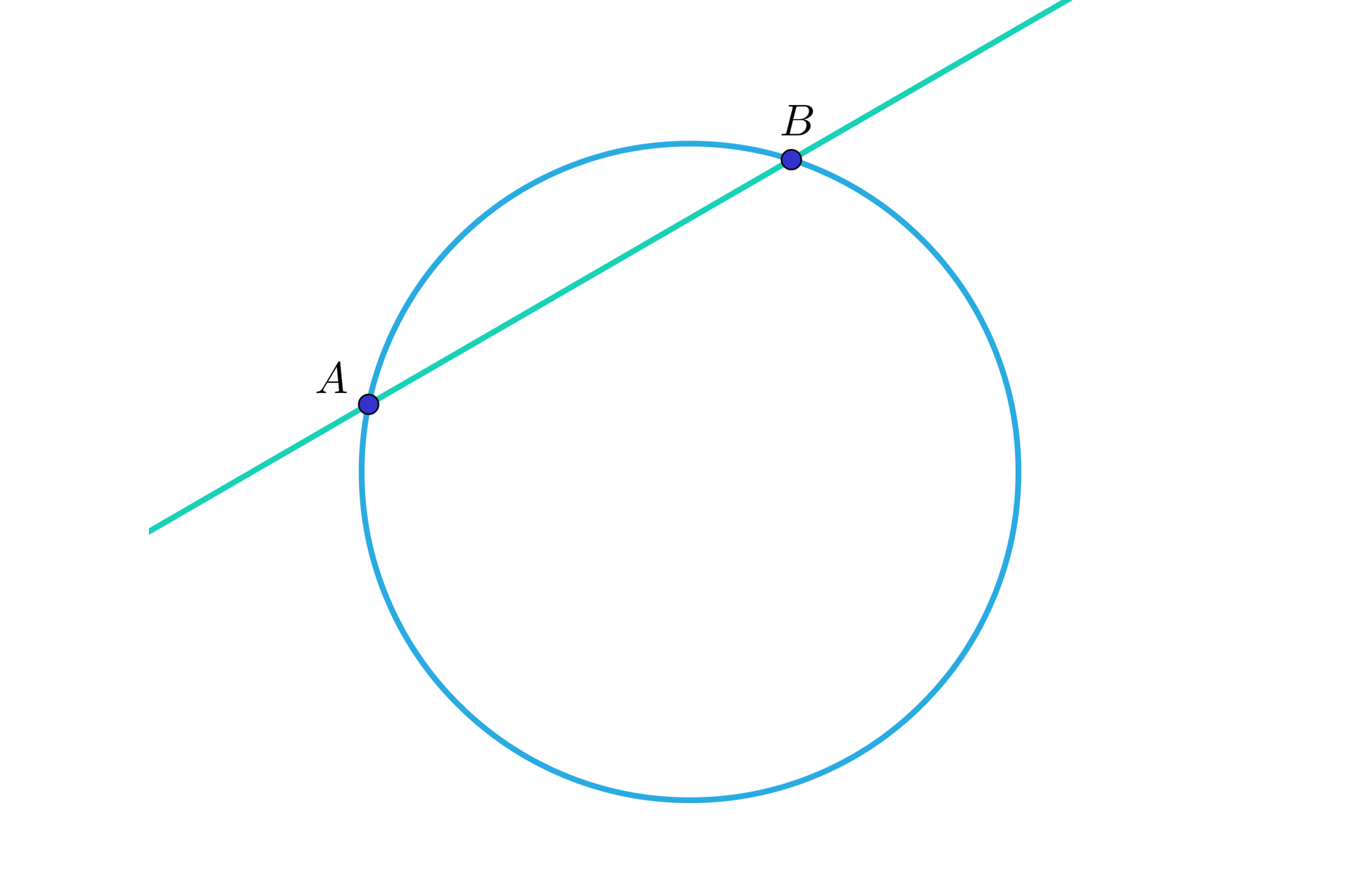
Grafika przedstawia okrąg przez który przechodzi prosta. Punkty przecięcia prostej z okręgiem podpisano A oraz B.

Wzajemne położenie okręgu i prostej na płaszczyźnie można określić badając odległość prostej od środka okręgu.

Jeżeli odległość środka okręgu od prostej jest mniejsza od długości promienia okręgu, to prosta i okrąg mają dwa punkty wspólne. Taką prostą nazywamy wtedy sieczną okręgusieczna okręgusieczną okręgu.

Odległość punktu $A = (x_{0}, y_{0})$ od prostej $A x + B y + C = 0$ opisuje wzór

d = \frac{|{A x}_{0} + {B y}_{0} + C|}{\sqrt{A^{2} + B^{2}}}

W naszym przypadku, odległość środka okręgu o równaniu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ od prostej $A x + B y + C = 0$ będącej sieczną, jest mniejsza od długości promienia, czyli:

d = \frac{|A \cdot a + B \cdot b + C|}{\sqrt{A^{2} + B^{2}}} < r

gdzie:
$O = (a, b)$ – środek okręgu,
$r$ – promień okręgu.

RFHiRTu5AwzKv

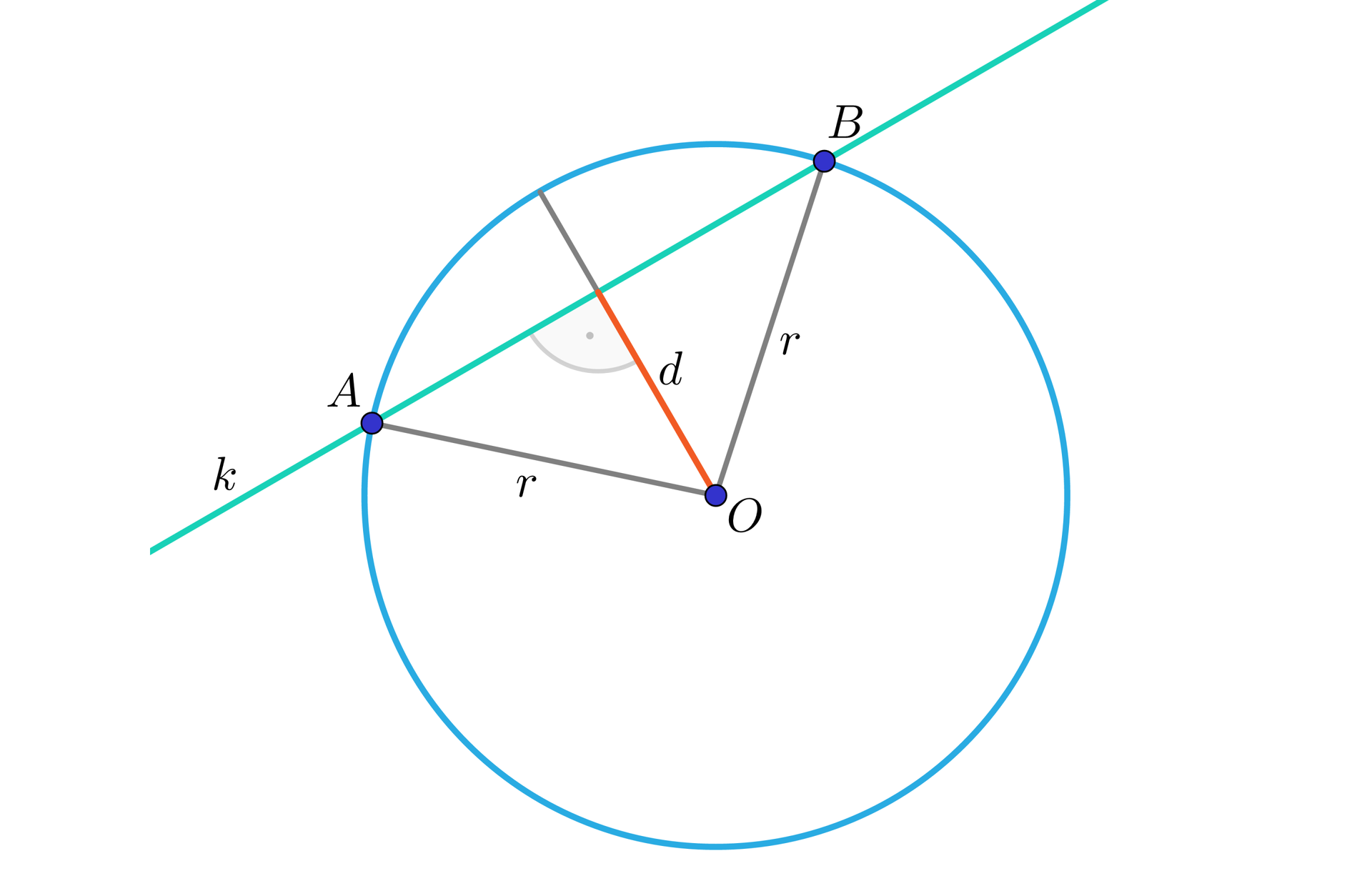
Grafika przedstawia okrąg o środku w punkcie O przez który przechodzi prosta k. Punkty przecięcia prostej z okręgiem podpisano A oraz B. Odcinki AO oraz BO podpisano literami r. Ze środka okręgu poprowadzono promień pod kątem prostym do prostej k. Odcinek leżący na tym promieniu, znajdujący się pomiędzy środkiem okręgu a prostą podpisano literą d.

Jeżeli odległość środka okręgu od prostej jest równa długości promienia okręgu, to prosta i okrąg mają jeden punkt wspólny. Taką prostą nazywamy wtedy styczną do okręgu. Z kolei jeśli odległość środka okręgu od prostej jest większa od długości promienia okręgu, to okrąg i prosta są rozłączne.

Przykład 1

Określimy wzajemne położenie prostej $3 x - y - 1 = 0$ i okręgu $x^{2} + y^{2} = 9$ .

Rozwiązanie:

Równanie $x^{2} + y^{2} = 9$ przedstawia okrąg o środku $O = (0, 0)$ i promieniu $r = 3$ .

Obliczamy odległość $d$ punktu $O$ od prostej o podanym równaniu.

$A = 3$ , $B = - 1$ , $C = - 1$ , $x_{0} = 0$ , $y_{0} = 0$ , $r = 3$ .

Zgodnie ze wzorem $d = \frac{|{A x}_{0} + {B y}_{0} + C|}{\sqrt{A^{2} + B^{2}}}$ , mamy zatem $d = \frac{|3 \cdot 0 + (- 1) \cdot 0 - 1|}{\sqrt{3^{2} + {(- 1)}^{2}}} = \frac{|- 1|}{\sqrt{10}} = \frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10}$ .

Tak więc $d = \frac{\sqrt{10}}{10} < 3 = r$ .

Rozwiązanie możemy również przedstawić graficznie, umieszczając w układzie współrzędnych okrąg o równaniu $x^{2} + y^{2} = 9$ i prostą $3 x - y - 1 = 0$ .

W układzie współrzędnych rysujemy okrąg o środku $O = (0, 0)$ i promieniu $r = 3$ oraz prostą $3 x - y - 1 = 0$ . Prosta przedstawiona w postaci kierunkowej $y = 3 x - 1$ przecina oś $X$ w punkcie $(\frac{1}{3}, 0)$ (wynika to z rozwiązania równania $0 = 3 x - 1$ ), natomiast oś $Y$ w punkcie $(0, - 1)$ .

R1PgLoiOCSJvB

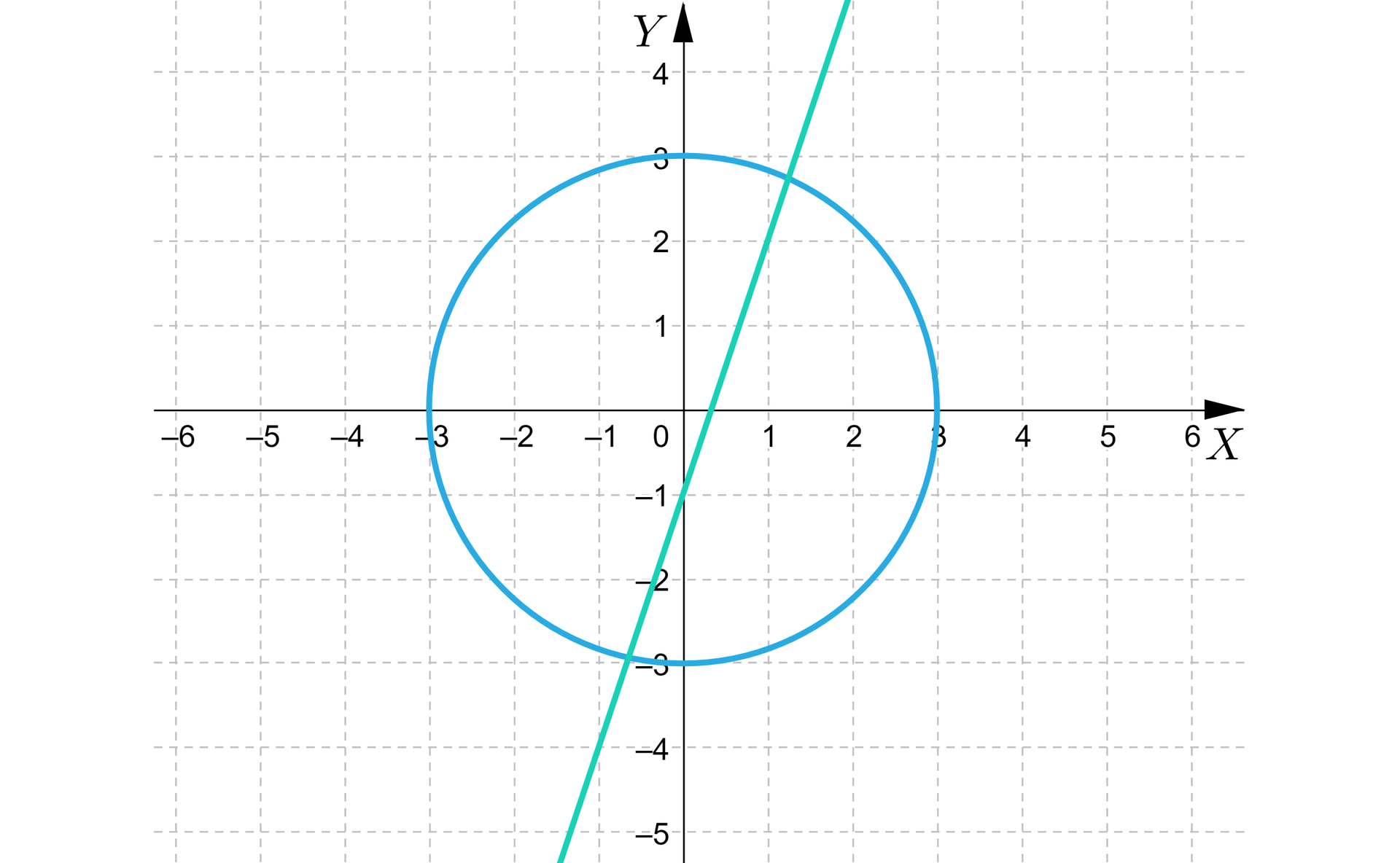
Grafika przedstawia układ współrzędnych z poziomą osią x od minus sześciu do sześciu i pionową osią y od minus pięciu do czterech. Na płaszczyźnie zaznaczono okrąg oraz prostą. Okrąg ma środek w środku układu współrzędnych i promień o długości trzy. Prosta przechodzi przez punkt początek nawiasu, 0, minus 1, zamknięcie nawiasu, oraz punkt początek nawiasu, 1, 2, zamknięcie nawiasu. Prosta przecina okrąg w dwóch punktach.

Prosta $3 x - y - 1 = 0$ jest zatem sieczną okręgu $x^{2} + y^{2} = 9$ .

Wzajemne położenie prostej $y = m x + n$ i okręgu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ możemy określić poprzez analizę liczby rozwiązań układu równań:

\{\begin{cases} y = m x + n \\ {(x - a)}^{2} + {(y - b)}^{2} = r^{2} \end{cases}

Po podstawieniu $y = m x + n$ do drugiego równania, otrzymujemy równanie kwadratowe.

Możliwe są trzy przypadki:

$∆ > 0$ – prosta ma z okręgiem dwa (różne) punkty wspólne – jest sieczną okręgusieczna okręgusieczną okręgu,
$∆ < 0$ – prosta nie ma punktu wspólnego z okręgiem,
$∆ = 0$ – prosta ma z okręgiem jeden punkt wspólny (podwójny), czyli jest styczną do okręgu.

Ważne!

Prosta $y = m x + n$ jest sieczną okręgu ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , gdy równanie kwadratowe wynikające z układu równań:

\{\begin{cases} y = m x + n \\ {(x - a)}^{2} + {(y - b)}^{2} = r^{2} \end{cases}

ma dwa rozwiązania.

Przykład 2

Sprawdzimy w jakich punktach prosta $x - y + 1 = 0$ przecina okrąg o równaniu $x^{2} + y^{2} + 2 x - 4 y - 4 = 0$ .

Rozwiązanie:

Prostą o równaniu $x - y + 1 = 0$ zapisujemy w postaci kierunkowej $y = x + 1$ .

Aby znaleźć punkty wspólne prostej i okręgu, rozwiązujemy układ równań:

$\{\begin{cases} y = x + 1 \\ x^{2} + y^{2} + 2 x - 4 y - 4 = 0 \end{cases}$

Podstawiamy $y = x + 1$ do równania $x^{2} + y^{2} + 2 x - 4 y - 4 = 0$ i otrzymujemy

$x^{2} + {(x + 1)}^{2} + 2 x - 4 \cdot (x + 1) - 4 = 0$ ,

$x^{2} + x^{2} + 2 x + 1 + 2 x - 4 x - 4 - 4 = 0$ ,

$2 x^{2} - 7 = 0$ .

Równanie $2 x^{2} - 7 = 0$ ma dwa rozwiązania: $x_{1} = \sqrt{\frac{7}{2}}$ i $x_{2} = - \sqrt{\frac{7}{2}}$ .

Ponieważ $y = x + 1$ , stąd $y_{1} = \sqrt{\frac{7}{2}} + 1$ i $y_{2} = - \sqrt{\frac{7}{2}} + 1$ .

Punkty $(\sqrt{\frac{7}{2}}, \sqrt{\frac{7}{2}} + 1)$ i $(- \sqrt{\frac{7}{2}}, - \sqrt{\frac{7}{2}} + 1)$ są punktami przecięcia siecznej $x - y + 1 = 0$ z okręgiem $x^{2} + y^{2} + 2 x - 4 y - 4 = 0$ .

Przykład 3

Obliczymy długość cięciwy, którą okrąg $x^{2} + y^{2} = 20$ odcina na prostej $5 x - 12 y + 44 = 0$ .

Rozwiązanie:

Sporządźmy poglądowy rysunek.

R7vTPjZ2TwGXH

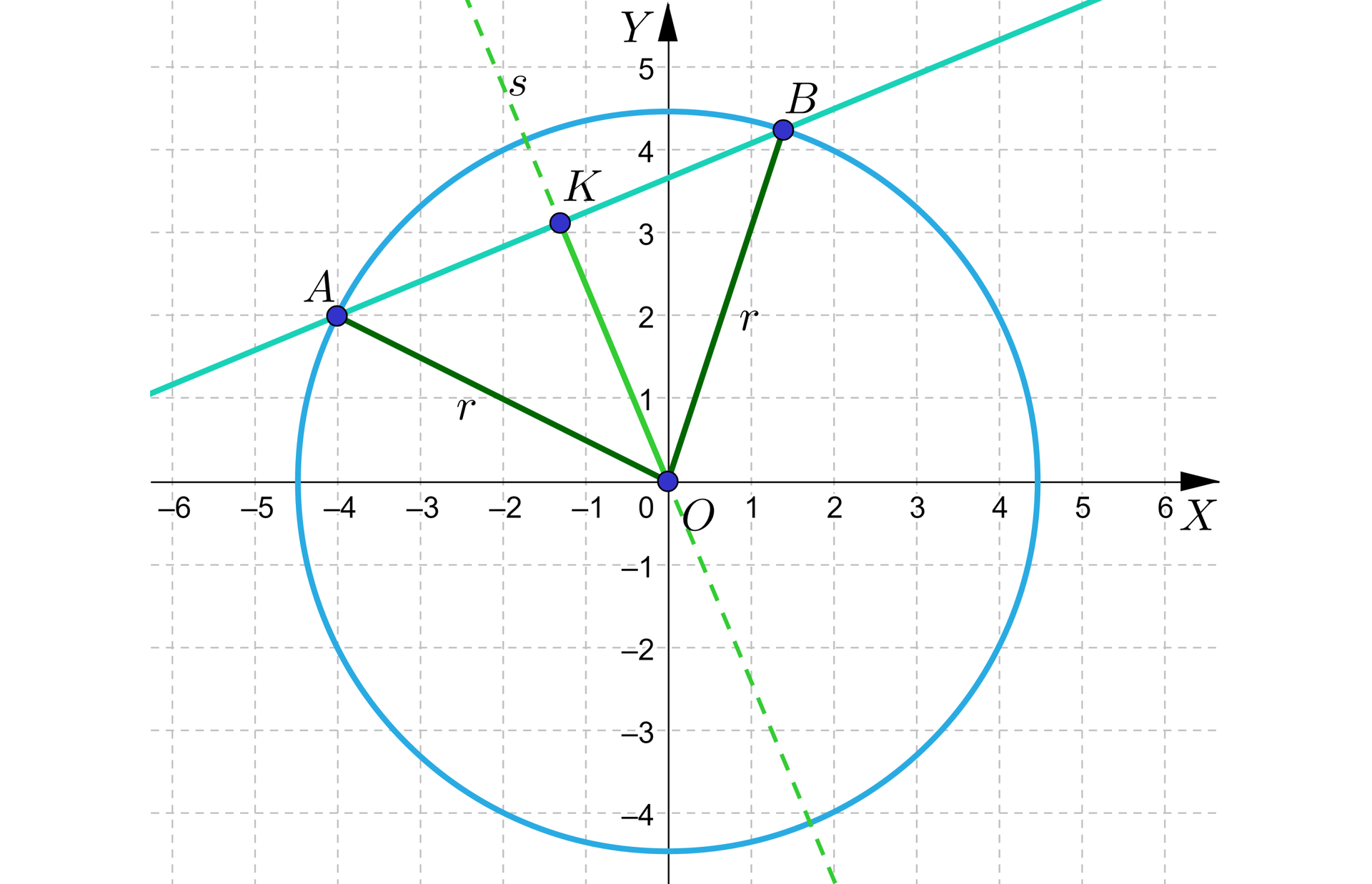
Grafika przedstawia układ współrzędnych z poziomą osią x od minus sześciu do sześciu i pionową osią y od minus czterech do pięciu. Na płaszczyźnie zaznaczono okrąg oraz dwie proste. Okrąg ma środek O w środku układ współrzędnych i przechodzi przez punkt początek nawiasu, 4, 2, zamknięcie nawiasu. Na okręgu zaznaczone są dwa punkty A oraz B. Współrzędne punktu A to początek nawiasu, minus 4 , 2, zamknięcie nawiasu. Natomiast punkt B znajduje się w pierwszej ćwiartce układu współrzędnych. Odcinki AO oraz BO podpisano literą r. Prosta przechodzi przez punkty A oraz B. Przez środek okręgu linią przerywaną poprowadzono prostą s. Przerywana prosta przecina pierwszą prostą pomiędzy punktami A i B. Punkt przecięcia się prostych podpisano literą K. Odcinek KO zaznaczono linią ciągłą.

Prosta $5 x - 12 y + 44 = 0$ przecina okrąg w punktach $A$ i $B$ . Długość odcinka $B$ jest długością cięciwy.

Symetralna $s$ cięciwy $A B$ jest do niej prostopadła, przechodzi przez punkt $O$ i dzieli cięciwę na dwie części o równej długości. Utworzony trójkąt $O K B$ jest prostokątny.

Obliczając odległość prostej $5 x - 12 y + 44 = 0$ od środka okręgu $x^{2} + y^{2} = 20$ , wyznaczymy długość odcinka $K O$ .

Równanie $x^{2} + y^{2} = 20$ przedstawia okrąg o środku $O = (0, 0)$ i promieniu $r = \sqrt{20}$ .

Obliczamy odległość $d$ punktu $O$ od prostej o równaniu $5 x - 12 y + 44 = 0$ .

$A = 5$ , $B = - 12$ , $C = 44$ , $x_{0} = 0$ , $y_{0} = 0$ .

Ze wzoru $d = \frac{|{A x}_{0} + {B y}_{0} + C|}{\sqrt{A^{2} + B^{2}}}$ , mamy zatem $d = \frac{|5 \cdot 0 + (- 12) \cdot 0 + 44|}{\sqrt{5^{2} + {(- 12)}^{2}}} = \frac{|44|}{\sqrt{169}} = \frac{44}{13}$ .

Punkt $K$ jest środkiem odcinka $A B$ , oznaczmy $|A K| = |K B| = x$ .

Ponieważ $|O B| = r$ , $|K O| = d$ , $|K B| = x$ , to z twierdzenia Pitagorasa dla trójkąta prostokątnego $O K B$ możemy zapisać: $d^{2} + x^{2} = r^{2}$ .

Po podstawieniu $r = \sqrt{20}$ , $d = \frac{44}{13}$ , otrzymujemy równanie ${(\frac{44}{13})}^{2} + x^{2} = {(\sqrt{20})}^{2}$ , z którego wyznaczymy $x$ .

$x^{2} = 20 - \frac{1936}{169} = \frac{3380 - 1936}{169} = \frac{1444}{169}$ , stąd $x = \frac{38}{13}$ .

Ponieważ $|A K| = |K B| = x$ i $K$ jest środkiem odcinka $A B$ , więc $|A B| = 2 x = 2 \cdot \frac{38}{13} = \frac{76}{13}$ .

Długość cięciwy, którą okrąg $x^{2} + y^{2} = 20$ odcina na prostej $5 x - 12 y + 44 = 0$ , wynosi $\frac{76}{13}$ .

Przykład 4

Z punktu $A$ okręgu poprowadzono dwie prostopadłe cięciwy: $A B$ i $A C$ . Udowodnij, że $B C$ jest średnicą tego okręgu.

Rozwiązanie:

Umieszczamy punkt $A$ w początku układu współrzędnych. Ponieważ cięciwy $A B$ i $A C$ są do siebie prostopadłe, to jeśli punkt $B$ umieścimy na osi $X$ , punkt $C$ znajdzie się na osi $Y$ .

$A = (0, 0)$ , $B = (b, 0)$ , $C = (0, c)$ .

R192aHGEkhaCb

Grafika przedstawia układ współrzędnych z poziomą osią x od minus dziewięciu do trzech i pionową osią y od minus dwóch do siedmiu. Na płaszczyźnie zaznaczono okrąg. Na okręgu zaznaczono trzy punkty A, B oraz C. Punkt A ma współrzędne początek nawiasu, 0, 0, zamknięcie nawiasu, punkt B ma współrzędne początek nawiasu, b, 0, zamknięcie nawiasu, punkt C ma współrzędne początek nawiasu, 0, c, zamknięcie nawiasu. Punkty A, B oraz C połączono w taki sposób, że utworzyły trójkąt prostokątny. O jednej przyprostokątnej leżącej na osi x i drugiej przyprostokątnej leżącej na osi y.

Niech $K$ będzie środkiem odcinka $B C$ , wtedy $K = (\frac{b}{2}, \frac{c}{2})$ . Obliczamy długości odcinków $K B$ , $K C$ i $K A$ :

${|K B|}^{2} = {(b - \frac{b}{2})}^{2} + {(0 - \frac{c}{2})}^{2} = {(\frac{b}{2})}^{2} + {(\frac{- c}{2})}^{2} = {(\frac{b}{2})}^{2} + {(\frac{c}{2})}^{2}$ ,

${|K C|}^{2} = {(0 - \frac{b}{2})}^{2} + {(c - \frac{c}{2})}^{2} = {(\frac{- b}{2})}^{2} + {(\frac{c}{2})}^{2} = {(\frac{b}{2})}^{2} + {(\frac{c}{2})}^{2}$ ,

${|K A|}^{2} = {(0 - \frac{b}{2})}^{2} + {(0 - \frac{c}{2})}^{2} = {(\frac{- b}{2})}^{2} + {(\frac{- c}{2})}^{2} = {(\frac{b}{2})}^{2} + {(\frac{c}{2})}^{2}$ .

Zatem $|K B| = |K C| = |K A|$ , czyli punkty $A$ , $B$ , $C$ są tak samo odległe od punktu $K$ . W związku z tym, $K$ jest środkiem okręgu przechodzącego przez punkty $A$ , $B$ , $C$ . W związku z powyższym, $B C$ jest średnicą danego okręgu.

Zauważmy, że mogliśmy rónież skorzystać z faktu, że kąt $B A C$ jest kątem prostym oraz że kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku.

Słownik

okrąg o środku O i promieniu r

zbiór wszystkich punktów $P$ płaszczyzny, których odległość od punktu $O$ jest równa $r$

sieczna okręgu

prosta, która ma dokładnie dwa punkty wspólne z okręgiem

cięciwa okręgu

odcinek siecznej ograniczony jej punktami przecięcia z okręgiem

Wprowadzenie

Animacja

Słownik