Przeczytaj
Jeśli funkcja jest różniczkowalna w punkcie i ma w tym punkcie ekstremum, to
Punkty, w których pochodna funkcji jest równa zeru nazywamy punktami stacjonarnymi.
Zerowanie się pochodnej jest warunkiem koniecznym istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem wystarczającym.
Funkcja może mieć ekstremum lokalne jedynie w punktach, w których jej pochodna nie istnieje albo istnieje i jest równa zeru.
Jeśli funkcja jest różniczkowalna w przedziale i dla oraz dla , to funkcja ma w punkcie minimum.
Jeśli funkcja jest różniczkowalna w przedziale i dla oraz dla , to funkcja ma w punkcie maksimum.
Algorytm szukania ekstremum funkcji
Niech funkcja będzie ciągła na przedziale i niech ma pochodną właściwą lub niewłaściwą poza skończoną liczbą punktów tego przedziału. Ekstrema tej funkcji szukamy postępując według następującego algorytmu:
Sprawdzamy, kiedy spełniony jest warunek konieczny istnienia ekstremum funkcji. W tym celu znajdujemy punkty zerowania się pochodnej funkcji oraz punkty, w których pochodna właściwa tej funkcji nie istnieje.
Następnie posługujemy się twierdzeniem o warunku wystarczającym istnienia ekstremum. Badamy zmianę „znaku” pochodnej w punktach stacjonarnych, tj. przy przejściu przez punkt, w którym pochodna zeruje się.
Określamy rodzaj ekstremum według następujących reguł:
Jeśli pochodna przy przejściu przez punkt stacjonarny zmienia znak z ujemnego na dodatni, to funkcja osiąga w tym punkcie minimum.
Jeśli pochodna przy przejściu przez punkt stacjonarny zmienia znak z dodatniego na ujemny, to funkcja osiąga w tym punkcie maksimum.
Jeśli pochodna przy przejściu przez punkt stacjonarny nie zmienia znaku, to funkcja nie posiada w tym punkcie ekstremum.
Wyznaczymy ekstrema lokalne następującej funkcji .
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze . Jej pochodna dana jest wzorem
, .
Na mocy pierwszego Twierdzenia o warunku koniecznym istnienia ekstremum, funkcja różniczkowalnafunkcja różniczkowalna może mieć ekstremum w punkcie, wtedy i tylko, gdy jej pochodna jest w tym punkcie jest równa zeru.
Sprawdźmy, kiedy pochodna .
Otrzymujemy kolejno:
, gdy , czyli lub .
Sprawdzamy warunek wystarczający istnienia ekstremum funkcji.
Badamy zmianę znaku pochodnej w otoczeniu punktów stacjonarnych korzystając z jej wykresu.
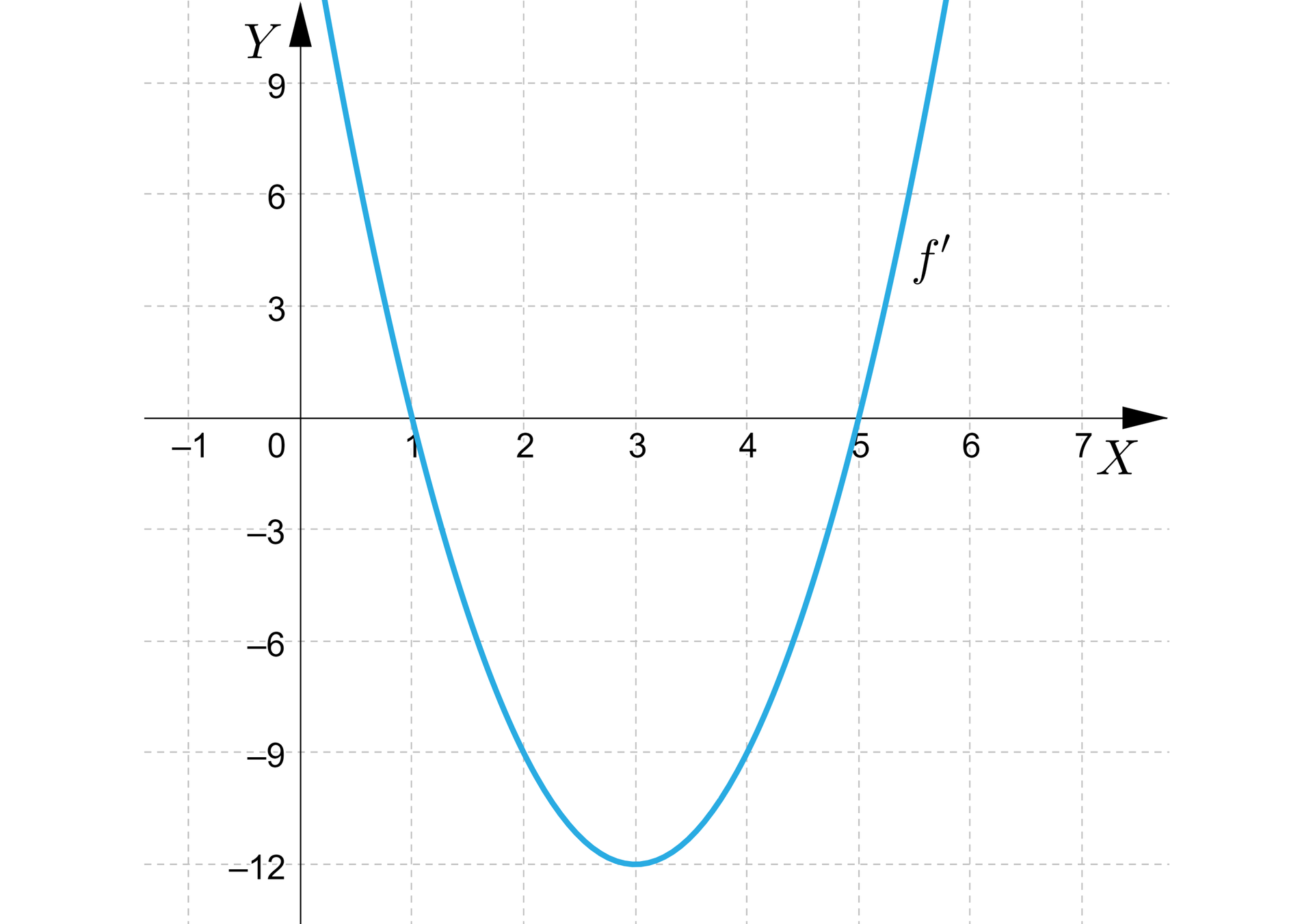
W otoczeniu punktu pochodna zmienia znak z dodatniego na ujemny, zatem w tym punkcie funkcja ma maksimum równe .
W otoczeniu punktu pochodna zmienia znak z ujemnego na dodatni, zatem w tym punkcie funkcja ma minimum równe .
Wyznaczymy ekstrema lokalne następującej funkcji dla .
Rozwiązanie:
Dziedziną funkcji jest zbiór .
Funkcja jako funkcja wymierna jest różniczkowalna w całej dziedzinie. Jej pochodna dana jest wzorem
, .
Sprawdzamy, kiedy spełniony jest warunek konieczny istnienia ekstremum, czyli kiedy pochodna .
Otrzymujemy kolejno:
, gdy , czyli , stąd lub .
Sprawdzamy warunek wystarczający istnienia ekstremum funkcji.
Badamy zmianę znaku pochodnej w otoczeniu punktów stacjonarnych korzystając z jej wykresu.
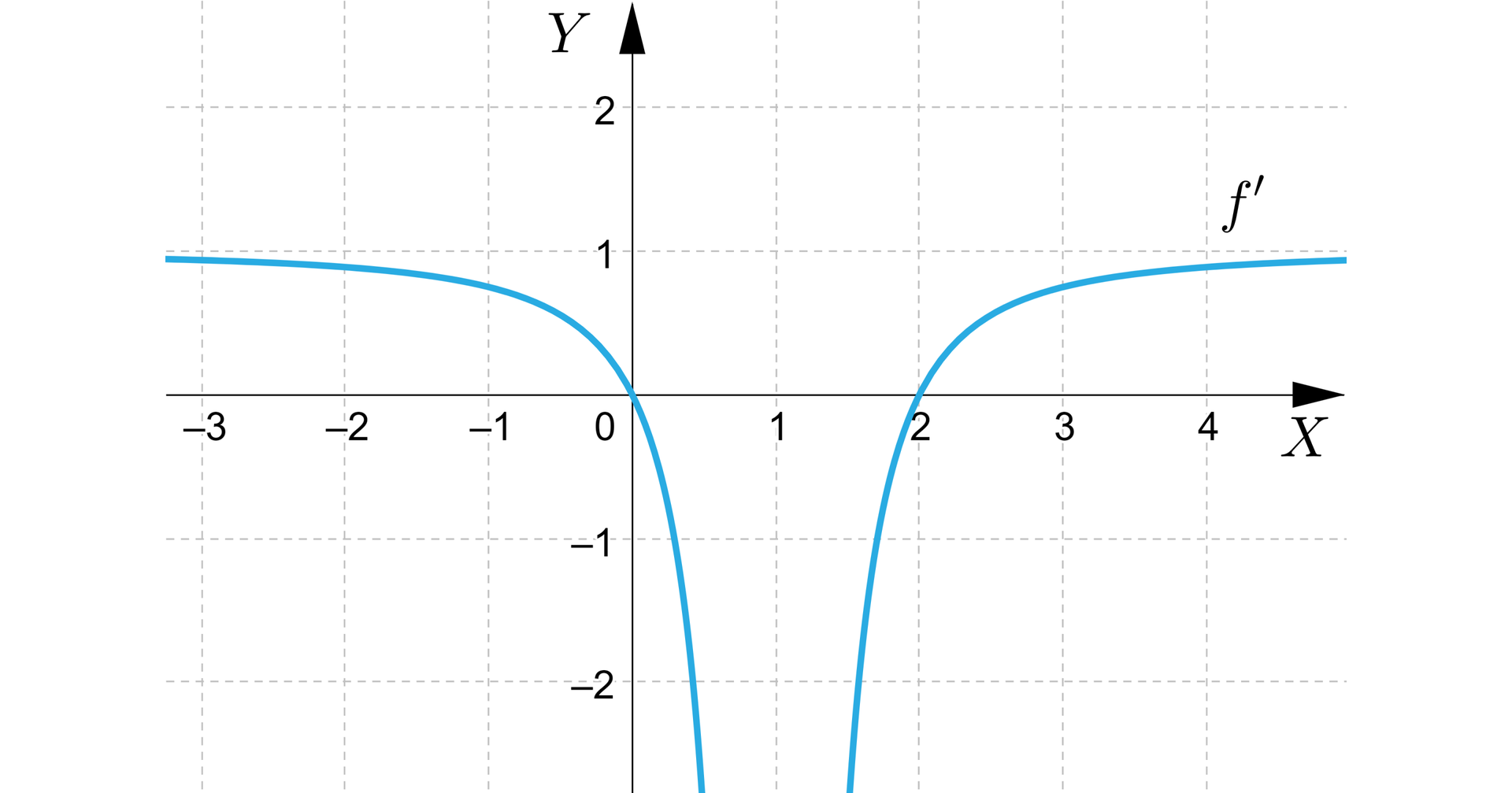
W otoczeniu punktu pochodna zmienia znak z dodatniego na ujemny, zatem w tym punkcie funkcja ma maksimum równe .
W otoczeniu punktu pochodna zmienia znak z ujemnego na dodatni, zatem w tym punkcie funkcja ma minimum równe .
Uwaga:
Dla rozważanej funkcji badanie znaku pochodnej można ograniczyć do badania znaku funkcji znajdującej się w liczniku pochodnej
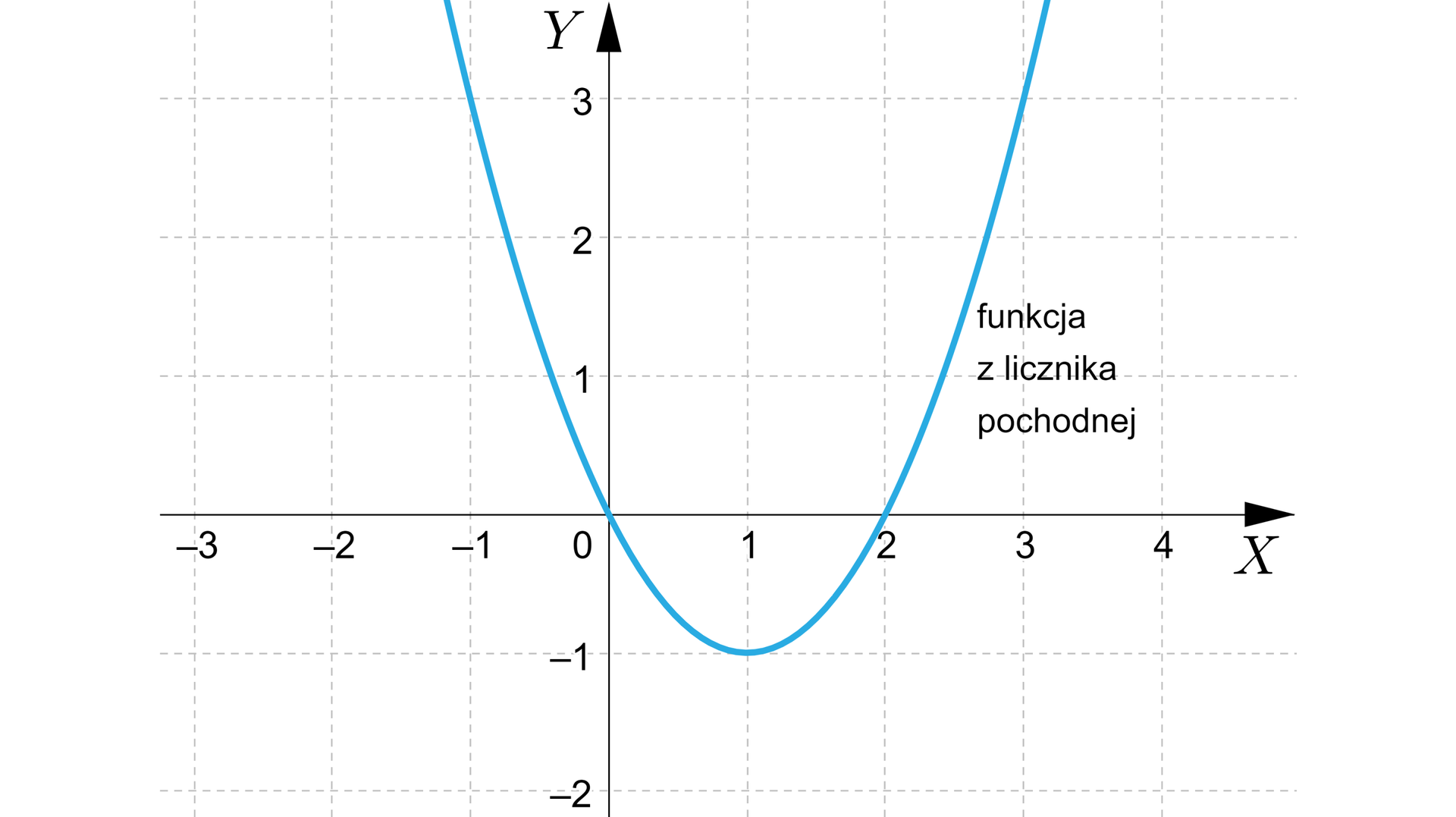
Zmiana znaku funkcji z licznika wpływa na znak całej pochodnej.
Wyznaczymy ekstrema lokalne następującej funkcji dla .
Rozwiązanie:
Dziedziną funkcji jest zbiór .
Funkcja jako funkcja wymierna jest różniczkowalna w całej dziedzinie. Jej pochodna dana jest wzorem
dla każdego argumentu ze zbioru .
Sprawdzamy, kiedy spełniony jest warunek konieczny istnienia ekstremum, czyli kiedy pochodna .
Otrzymujemy kolejno:
, gdy , czyli , stąd .
Sprawdzamy warunek wystarczający istnienia ekstremum funkcji.
Badamy zmianę znaku pochodnej w otoczeniu punktów stacjonarnych.
Otrzymujemy kolejno
,
,
.
,
,
.
W otoczeniu punktu pochodna zmienia znak z ujemnego na dodatni, zatem w tym punkcie funkcja ma minimum równe .
Punkt nie należy do dziedziny funkcji (ani pochodnej) zatem funkcja nie może mieć w nim ekstremum.
Sprawdzimy, ile ekstremów posiada funkcja w zależności od wartości parametru .
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze . Jej pochodna dana jest wzorem
.
Otrzymujemy kolejno
dla pochodna dla każdego argumentu z dziedziny funkcji. Zatem dla żadnego punktu z dziedziny nie jest spełniony warunek konieczny, ani wystarczający istnienia ekstremum funkcji. Funkcja nie ma ekstremum.
dla pochodna dla każdego argumentu z dziedziny funkcji. Istnieją zatem punkty, dla których spełniony jest warunek konieczny istnienia ekstremum funkcji, ale nie jest spełniony warunek wystarczający istnienia ekstremum funkcji, pochodna nie zmienia znaku. Zatem funkcja nie ma ekstremum.
dla pochodna dla każdego argumentu z dziedziny funkcji. Pochodna jest funkcją kwadratową, której wyróżnik dla . Stąd wynika, że pochodna ma dwa miejsca zerowe. Z własności funkcji kwadratowej posiadającej dwa miejsca zerowe wynika, że w otoczeniu tych miejsc pochodna zmienia znak. Zatem funkcja ma dwa ekstrema.
O funkcji wiadomo, że w punkcie posiada ekstremum równe . Znajdziemy wartości współczynników i oraz pozostałe ekstrema funkcji (jeśli je posiada).
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze . Jej pochodna dana jest wzorem
.
Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum funkcji wiemy, że funkcja ma punkty stacjonarne, wtedy i tylko wtedy, gdy . Zatem oraz .
Otrzymujemy kolejno
,
,
stad , .
Zatem pochodna funkcji dana jest wzorem .
Miejscami zerowymi pochodnej są punkty (warunek koniczny istnienia ekstremum funkcji) i .
Pochodna jest dodatnia dla oraz ujemna dla .
Zatem funkcja posiada drugie ekstremu w punkcie i jest ono równe .
Słownik
funkcję nazywamy różniczkowalną jeśli ma pochodną w każdym punkcie dziedziny