Przeczytaj

Figura środkowosymetryczna

Figurę mającą środek symetrii nazywamy figurą środkowosymetryczną.

środek symetrii figury

Definicja: środek symetrii figury

Punkt $O$ nazywamy środkiem symetrii figury, jeśli symetria o środku $O$ przekształca tę figurę na nią samą.

W poniższych przykładach zaprezentujemy kilka figur środkowosymetrycznych i wyznaczymy ich środki symetrii w układzie współrzędnych.

Odcinek jest figurą środkowosymetryczną, a środkiem symetrii odcinka jest jego środek.

Przykład 1

Wyznaczymy środek symetrii odcinka $A B$ , gdy $A = (- 2, 1)$ i $B = (4, 2)$ .

RDbNwQOsY2D0G

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 2 do czterech. Na płaszczyźnie zaznaczony jest odcinek o początku w punkcie A o współrzędnych: początek nawiasu, minus 2, 1, zamknięcie nawiasu i końcu w punkcie B o współrzędnych: początek nawiasu, 4, 2, zamknięcie nawiasu. Środek symetrii oznaczono literą O.

Rozwiązanie:

Środek symetrii $O = (x_{0}, y_{0})$ jest środkiem odcinka $A B$ .

Korzystamy ze wzorów na środek odcinka:

$x_{0} = \frac{x_{A} + x_{B}}{2}$ , $y_{0} = \frac{y_{A} + y_{B}}{2}$ .

Dla danych punktów otrzymujemy: $x_{0} = \frac{x_{A} + x_{B}}{2} = \frac{- 2 + 4}{2} = 1$ i $y_{0} = \frac{y_{A} + y_{B}}{2} = \frac{1 + 2}{2} = \frac{3}{2}$ .

Środkiem symetrii odcinka $A B$ jest punkt $O = (1, \frac{3}{2})$ .

Okrąg i koło są figurami środkowosymetrycznymi, a środkiem symetrii jest środek okręgu, koła.

Przykład 2

Podamy współrzędne środka symetrii okręgu o równaniu ${(x - 1)}^{2} + y^{2} = 4$ .

Rozwiązanie:

We współrzędnych kartezjańskich równanie okręgu o środku $O = (a, b)$ i promieniu $r$ ma postać:

${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ .

Z równania ${(x - 1)}^{2} + y^{2} = 4$ odczytujemy współrzędne środka okręgu $O = (1, 0)$ oraz długość promienia $r = 2$ .

R1enih0ylJcVz

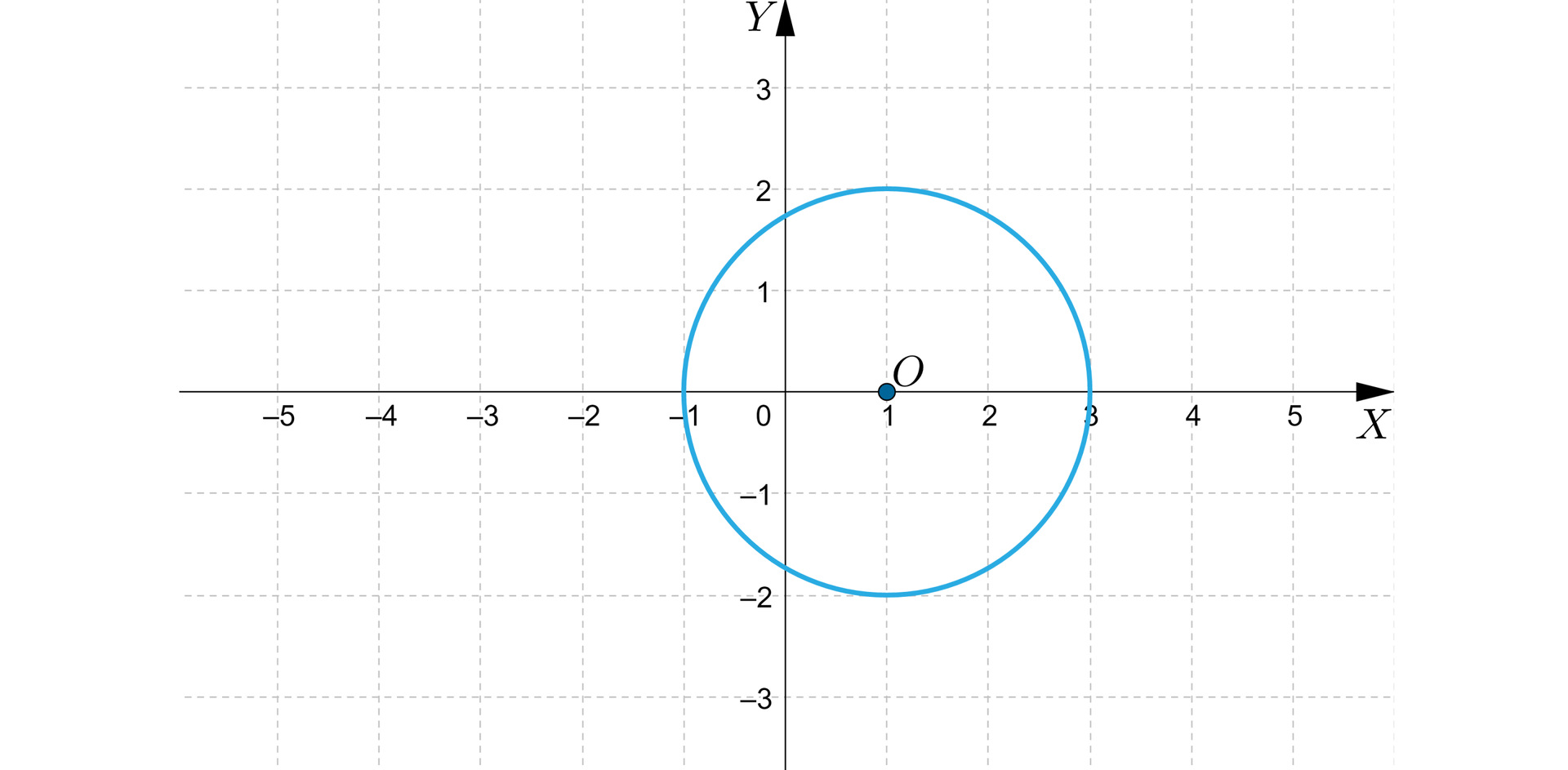
Grafika przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 3 do trzy. Na płaszczyźnie zaznaczony jest okrąg przecinający oś x w dwóch punktach kolejno: początek nawiasu, minus 1, zero, zamknięcie nawiasu oraz początek nawiasu, 3, 0, zamknięcie nawiasu. Środek okręgu znajduje się w punkcie: początek nawiasu, 1, 0, zamknięcie nawiasu.

Środkiem symetrii okręgu ${(x - 1)}^{2} + y^{2} = 4$ jest punkt $O = (1, 0)$ .

Przykład 3

Znajdziemy środek symetriiśrodek symetrii figuryśrodek symetrii okręgu przechodzącego przez punkty $A = (- 3, - 1)$ i $B = (1, - 3)$ , wiedząc, że środek okręgu leży na prostej $m$ o równaniu $y = 3 x + 2$ . Podamy równanie tego okręgu.

RxaAKRXSPMxB5

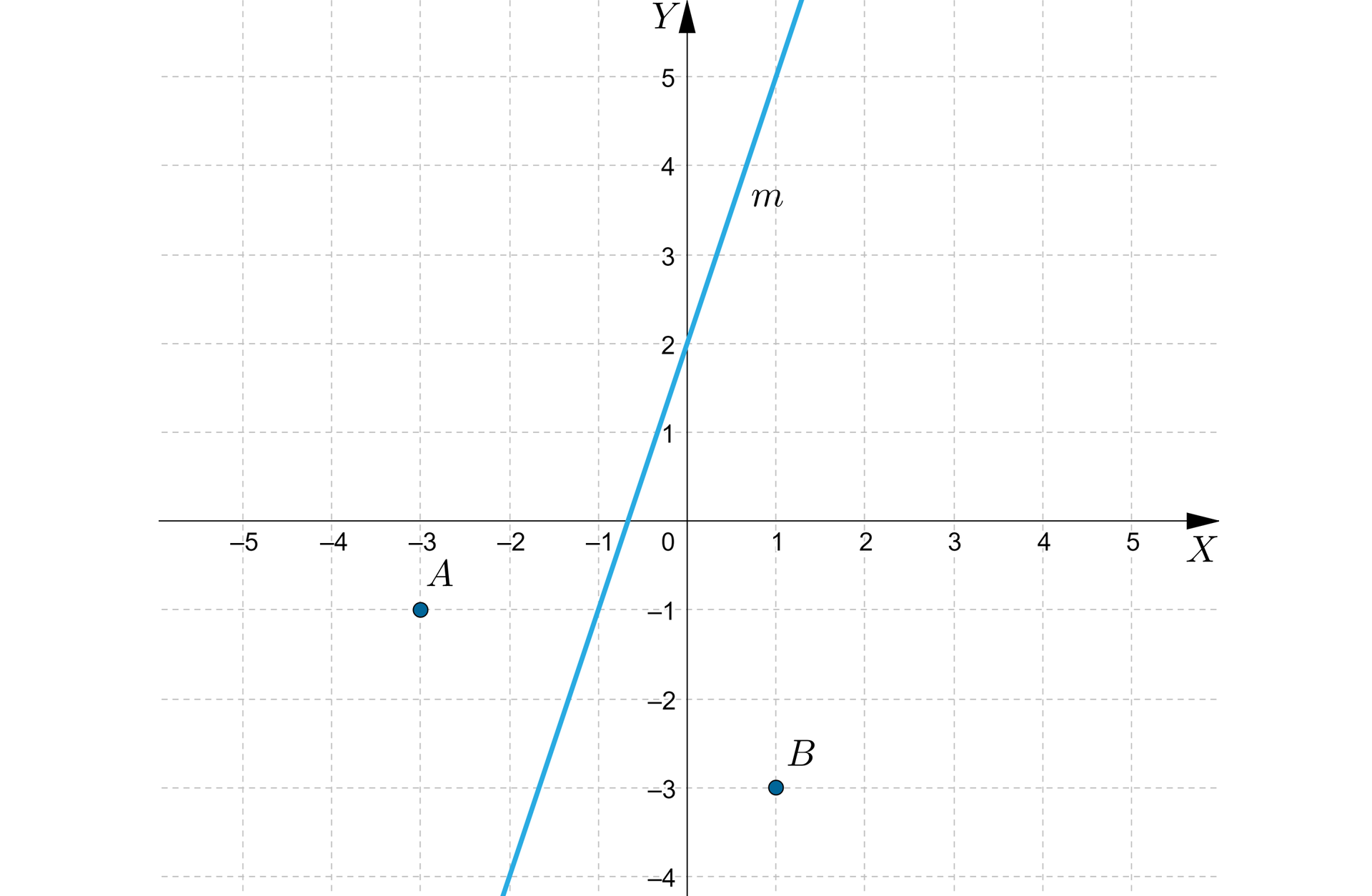
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do pięciu. Na płaszczyźnie znajduje się prosta m oraz dwa punkty A i B. Prosta jest ukośna i przecina oś y w punkcie: początek nawiasu, 0, 2, zamknięcie nawiasu. Współrzędne punktów to kolejno: punkt A: początek nawiasu, minus 3, minus 1, zamknięcie nawiasu oraz punkt B: początek nawiasu, 1, minus 3, zamknięcie nawiasu.

Rozwiązanie:

Środek okręgu leży na przecięciu symetralnej odcinka $A B$ , z prostą o równaniu $y = 3 x + 2$ .

symetralna odcinka

Definicja: symetralna odcinka

Symetralną odcinka nazywamy prostą prostopadłą do odcinka i dzielącą go na dwie równe części.

Wyznaczamy równanie symetralnej odcinka $A B$ .

Zapiszemy równanie prostej $k$ przechodzącej przez punkty $A = (- 3, - 1)$ i $B = (1, - 3)$ w postaci $y = a x + b$ .
W tym celu rozwiązujemy układ równań:
$\{\begin{cases} - 1 = a \cdot (- 3) + b \\ - 3 = a \cdot 1 + b \end{cases}$
Odejmujmy od pierwszego równania drugie i otrzymujemy:

$2 = - 4 \cdot a$ , stąd $a = - \frac{1}{2}$ .

Z drugiego równania otrzymujemy $b = - 3 - a$ , a w rezultacie $b = - 3 - (- \frac{1}{2}) = - \frac{5}{2}$ .

Równanie prostej $k$ przechodzącej przez punkty $A$ i $B$ to $k$ : $y = - \frac{1}{2} x - \frac{5}{2}$ .

R1T8TmxaEvDnS

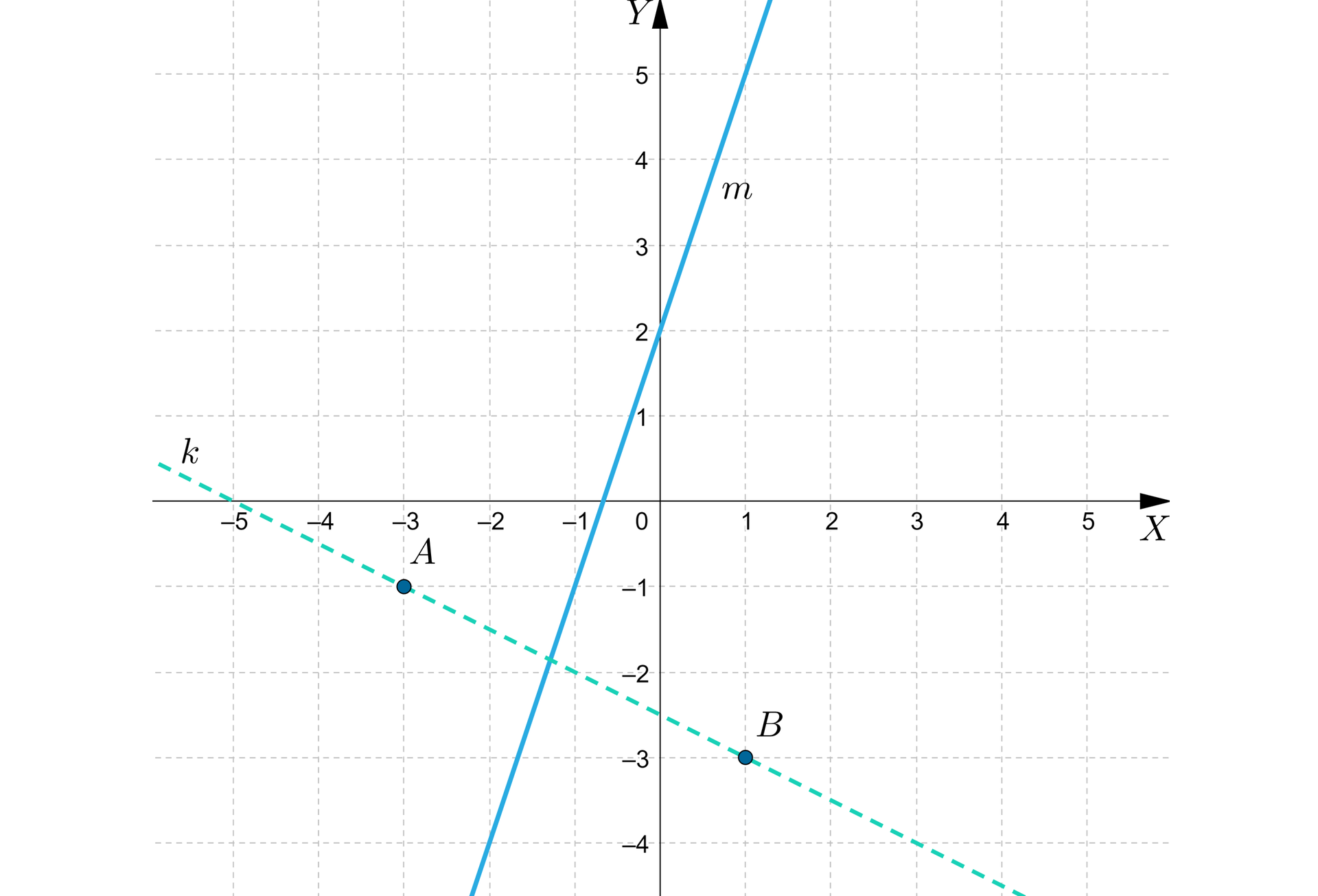
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do pięciu. Na płaszczyźnie znajdują się dwie proste m i k. Ukośna prosta m przecina oś y w punkcie: początek nawiasu, 0, 2, zamknięcie nawiasu. Prosta k namalowana linią przerywaną poprowadzona jest przez dwa punkty kolejno: punkt A o współrzędnych: początek nawiasu, minus 3, minus 1, zamknięcie nawiasu oraz punkt B o współrzędnych: początek nawiasu, 1, minus 3, zamknięcie nawiasu. Prosta k przecina oś x w punkcie: początek nawiasu, minus 5, 0, zamknięcie nawiasu.

Interesuje nas wartość współczynnika kierunkowego prostej $k$ przechodzącej przez punkty $A$ i $B$ , ponieważ szukamy równania symetralnej, która jest do prostej $k$ prostopadła.

prostopadłość prostych

Reguła: prostopadłość prostych

Jeżeli proste $y = a_{1} x + b_{1}$ i $y = a_{2} x + b_{2}$ są prostopadłe to:
$a_{2} = - \frac{1}{a_{1}}$ .

Ponieważ w naszym przypadku $a_{1} = - \frac{1}{2}$ , to z warunku prostopadłości prostych wynika, że:

$a_{2} = - \frac{1}{(- \frac{1}{2})} = 2$ .

Symetralna odcinka $A B$ jest zatem postaci $y = 2 x + b_{2}$ .

Ponieważ symetralna odcinka jest do tego odcinka prostopadła i przechodzi przez jego środek, musimy wyznaczyć współrzędne środka odcinka $A B$ , gdzie:
$A = (- 3, - 1)$ i $B = (1, - 3)$ .

Oznaczmy przez $P$ środek odcinka $A B$ :

$P = (x_{P}, y_{p})$ , gdzie $x_{P} = \frac{x_{A} + x_{B}}{2}$ , $y_{P} = \frac{y_{A} + y_{B}}{2}$ .

Otrzymujemy stąd:

$x_{P} = \frac{x_{A} + x_{B}}{2} = \frac{- 3 + 1}{2} = - 1$

oraz

$y_{P} = \frac{y_{A} + y_{B}}{2} = \frac{- 1 + (- 3)}{2} = - 2$ .

Zapiszemy teraz równanie prostej $l$ (symetralnej odcinka) przechodzącej przez punkt $P = (- 1, - 2)$ .

Prosta $l$ dana wzorem $y = 2 x + b_{2}$ przechodzi przez punkt $P = (- 1, - 2)$ , a zatem spełniona jest równość:

$- 2 = 2 \cdot (- 1) + b_{2}$ , stąd $b_{2} = 0$ .

Równanie prostej $l$ ma zatem postać $y = 2 x$ .

R1AIelDYTnjis

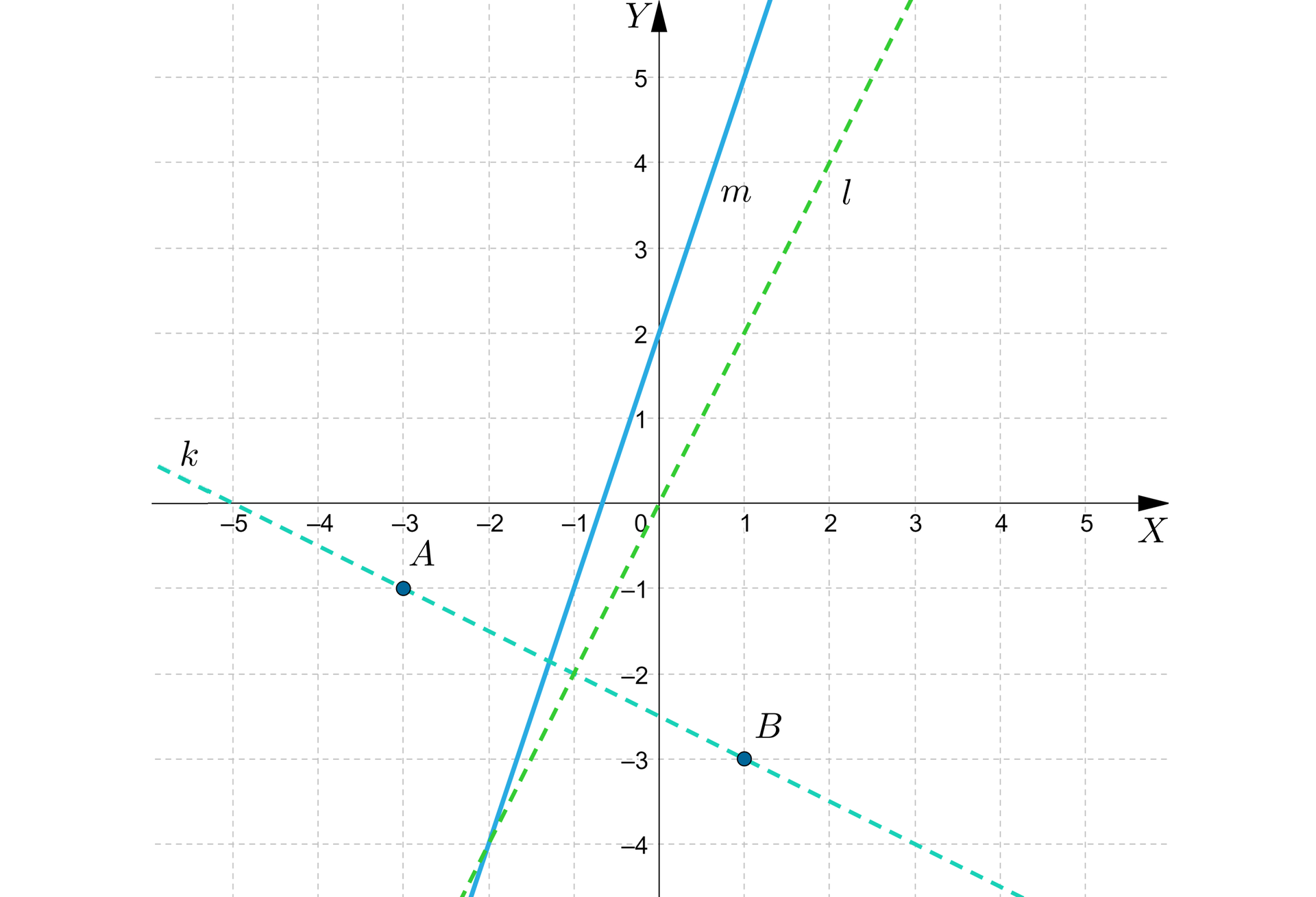
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 4 do pięciu. Na płaszczyźnie znajdują się 3 proste m, k oraz l. Prosta m przecina oś y w punkcie: początek nawiasu, 0, 2, zamknięcie nawiasu. Prosta k namalowana linią przerywaną poprowadzona jest przez 2 punkty kolejno: punkt A o współrzędnych: początek nawiasu, minus 3, minus 1, zamknięcie nawiasu oraz punkt B o współrzędnych: początek nawiasu, 1, minus 3, zamknięcie nawiasu. Prosta k przecina oś x w punkcie: początek nawiasu, minus 5, 0, zamknięcie nawiasu. Prosta l namalowana linią przerywaną przechodzi przez środek układu współrzędnych oraz przecina prostą m w punkcie: początek nawiasu, minus 2, minus 4, zamknięcie nawiasu.

Środek okręgu leży na przecięciu symetralnej odcinka $A B$ , czyli w naszym przypadku prostej $l$ o równaniu $y = 2 x$ , z prostą $m$ o równaniu $y = 3 x + 2$ .

W celu znalezienie punktu przecięcia rozwiązujemy układ równań:

$\{\begin{cases} y = 2 x \\ y = 3 x + 2 \end{cases}$

Po podstawieniu otrzymujemy równość $2 x = 3 x + 2$ .

Po rozwiązaniu otrzymujemy punkt przecięcia rozważanych prostych $O = (- 2, - 4)$

ReSVwRlCPqb24

Obliczymy teraz promień okręgu wykorzystując wzór na odległość punktów $A = (x_{1}, y_{1})$ i $B = (x_{2}, y_{2})$ :

$|A B| = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$

Skoro $r = |O A| = |O B|$ oraz $A = (- 3, - 1)$ i $O = (- 2, - 4)$ , więc mamy równość:

$r = |O A| = \sqrt{{(- 2 + 3)}^{2} + {(- 4 + 1)}^{2}} = \sqrt{{(1)}^{2} + {(- 3)}^{2}} = \sqrt{10}$

Równanie okręgu o środku $S = (a, b)$ i promieniu $r$ ma postać ${(x - a)}^{2} + {(y - b)}^{2} = r^{2}$ , co w naszym przypadku daje ${(x + 2)}^{2} + {(y + 4)}^{2} = 10$ .

Środkiem symetrii okręgu jest punkt $O = (- 2, - 4)$ .

Dowolny równoległobok jest figurą środkowosymetryczną. Środkiem symetrii równoległoboku jest punkt przecięcia przekątnych.

Przykład 4

Dane są wierzchołki $A = (- 3, 7)$ , $B = (- 5, 7)$ i $C = (2, 5)$ równoległoboku. Podaj współrzędne środka symetrii tego równoległoboku oraz współrzędne czwartego wierzchołka.

Rozwiązanie:

Środek symetrii równoległoboku leży na przecięciu przekątnych tego równoległoboku.

R15ftQo0j4pXC

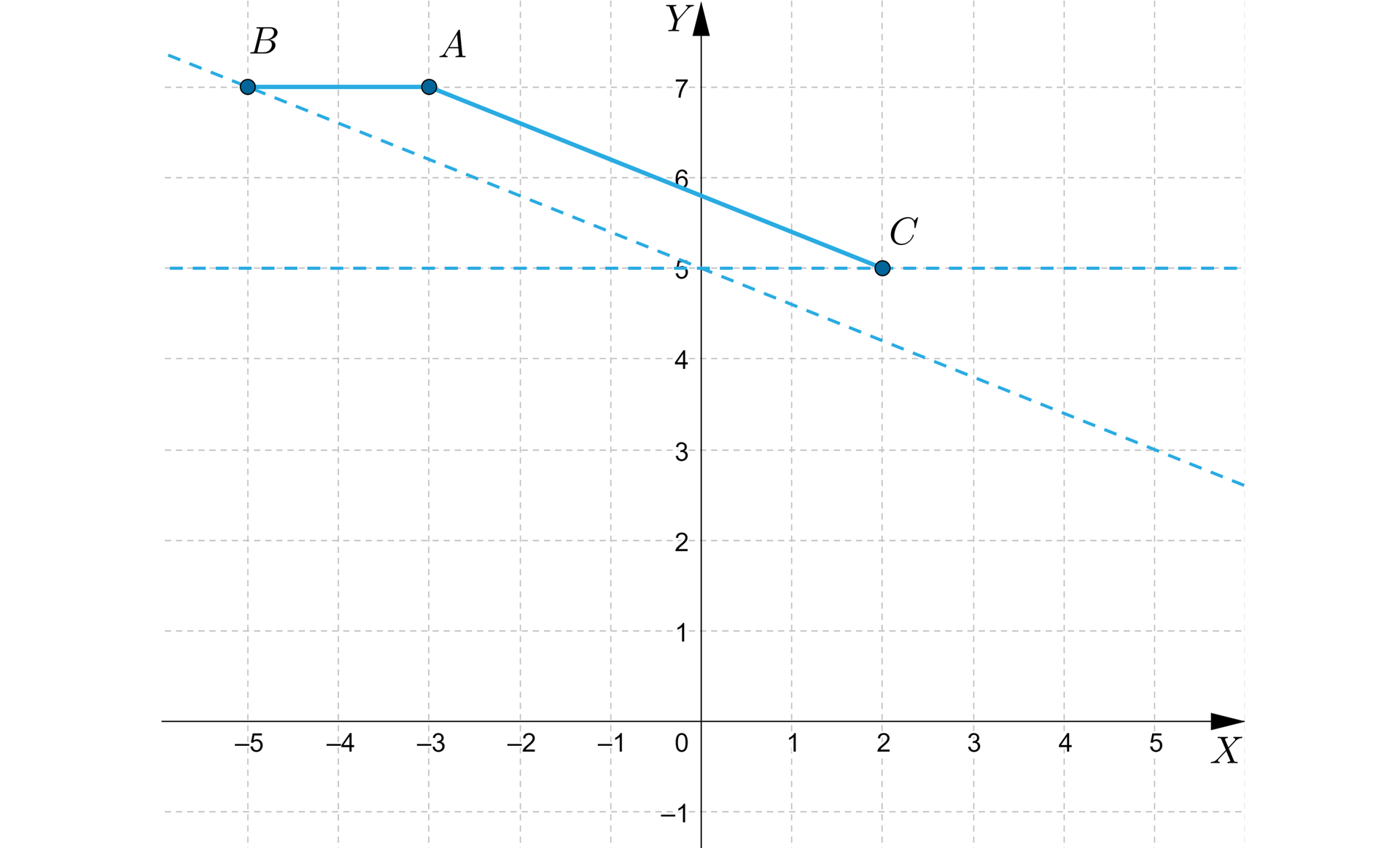
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus jeden do siedmiu. Na płaszczyźnie znajdują się 3 punkty, oraz dwie proste. Współrzędne punktów to kolejno: punkt B: początek nawiasu, minus 5, 7, zamknięcie nawiasu, punkt A: początek nawiasu, minus, 3, 7, zamknięcie nawiasu i punkt C: początek nawiasu, 2, 5, zamknięcie nawiasu. Punkty B i A tworzą jeden odcinek, natomiast punkty A i C tworzą drugi odcinek. Jedna prosta namalowana linią przerywaną przechodzi przez punkt B oraz przecina oś y w punkcie początek nawiasu, 0, 5, zamknięcie nawiasu, jest ona równoległa do odcinka AC. Druga prosta przechodzi przez punkt C i również przecina oś y w punkcie początek nawiasu, 0, 5, zamknięcie nawiasu, jest ona równoległa do odcinka BA. Proste przecinają się w punkcie: początek nawiasu, 0, 5, zamknięcie nawiasu. Proste są namalowane linią przerywaną.

Z rysunku wynika, że punkt przecięcia przekątnych leży na odcinku $B C$ .

przekątne równoległoboku

Własność: przekątne równoległoboku

Przekątne równoległoboku dzielą się na połowy.

Korzystając z powyższej własności, zastosujemy wzór na środek odcinka - w tym przypadku wyznaczymy środek $O = (x_{0}, y_{0})$ odcinka $B C$ :

$x_{0} = \frac{x_{B} + x_{C}}{2}$ , $y_{0} = \frac{y_{B} + y_{C}}{2}$ .

Otrzymujemy w ten sposób:

$x_{0} = \frac{x_{B} + x_{C}}{2} = \frac{- 5 + 2}{2} = - \frac{3}{2}$ ,

$y_{0} = \frac{y_{B} + y_{C}}{2} = \frac{7 + 5}{2} = 6$ .

Środkiem odcinka $B C$ jest punkt $O = (- \frac{3}{2}, 6)$ .

R8fMSsYgVe1c5

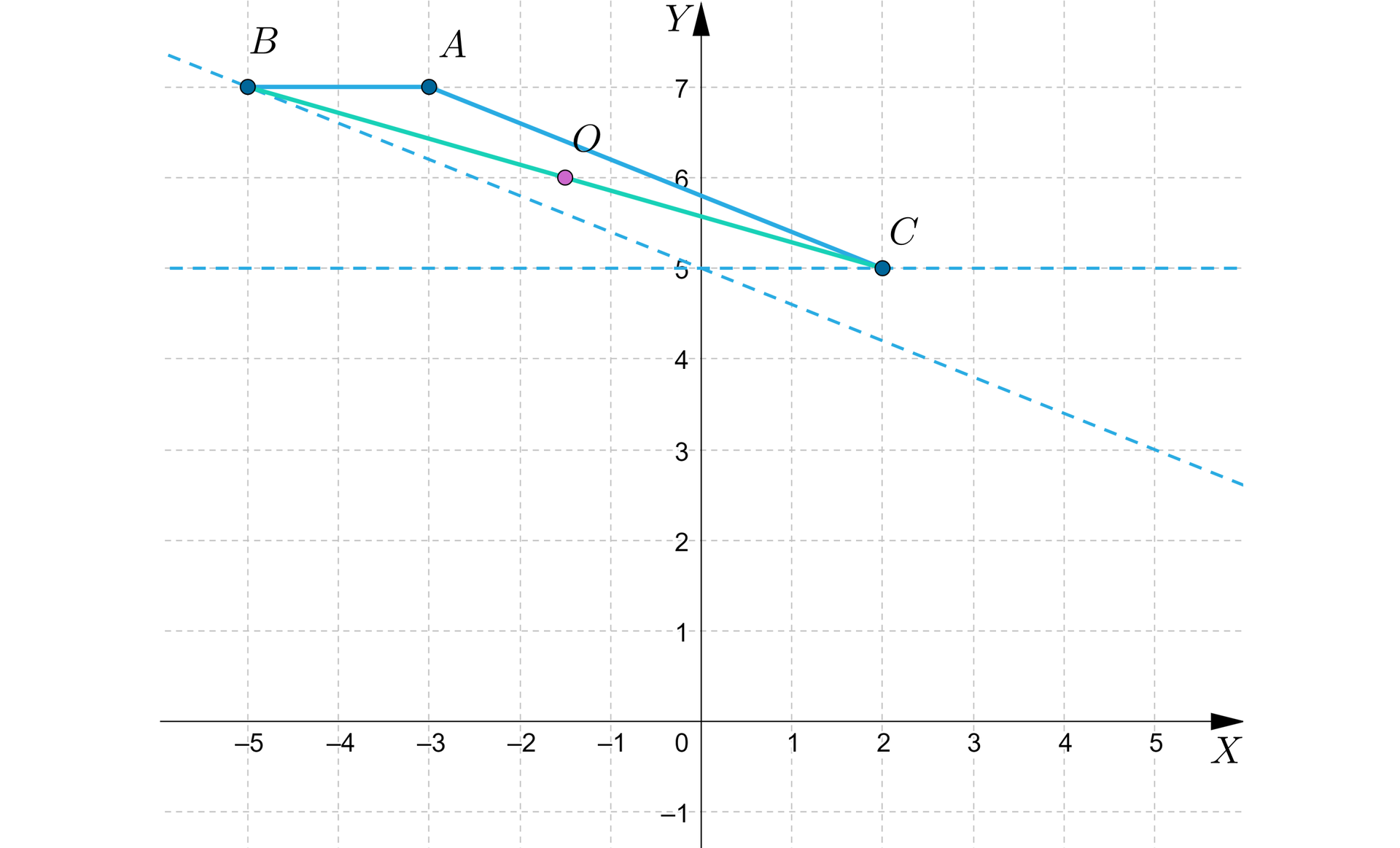
Zauważmy, że punkt $O$ jest również środkiem odcinka $A D$ . Zatem, korzystając z powyższych wzorów możemy wyznaczyć współrzędne punktu $D = (x_{D}, y_{D})$ .

$x_{0} = \frac{x_{A} + x_{D}}{2}$ , $y_{0} = \frac{y_{A} + y_{D}}{2}$ .

Mamy $x_{0} = \frac{x_{A} + x_{D}}{2} = \frac{- 3 + x_{D}}{2} = - \frac{3}{2}$ .

Otrzymujemy w ten sposób $x_{D} = 0$ .

Podobnie, $y_{0} = \frac{y_{A} + y_{D}}{2} = \frac{7 + y_{D}}{2} = 6$ , a stąd $y_{D} = 5$ .

W rezultacie otrzymujemy punkt $D = (0, 5)$ , będący czwartym wierzchołkiem równoległoboku.

R1W2Zhv6Ay47N

Ilustracja przedstawia układ wspóIlustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus jeden do siedmiu. Na płaszczyźnie znajdują się cztery punkty połączone odcinkami oraz jeden punkt narysowany wewnątrz powstałego z odcinków równoległoboku. Współrzędne punktów będących wierzchołkami równoległoboku to kolejno : punkt B: początek nawiasu, minus 5, 7, zamknięcie nawiasu, punkt A: początek nawiasu, minus 3, 7, zamknięcie nawiasu, punkt D: początek nawiasu, 0, 5, zamknięcie nawiasu, punkt C: początek nawiasu, 2, 5, zamknięcie nawiasu. Wewnątrz powstałego z odcinków równoległoboku jest punkt O, znajduje się on w drugiej ćwiartce układu współrzędnych, a jego druga współrzędna ma wartość 6.łrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do siedmiu. Na płaszczyźnie znajdują się cztery punkty połączone odcinkami oraz jeden punkt narysowany wewnątrz powstałego z odcinków równoległoboku. Współrzędne punktów będących wierzchołkami równoległoboku to kolejno : punkt B: początek nawiasu, minus 5, 7, zamknięcie nawiasu, punkt A: początek nawiasu, minus 3, 7, zamknięcie nawiasu, punkt D: początek nawiasu, 0, 5, zamknięcie nawiasu, punkt C: początek nawiasu, 2, 5, zamknięcie nawiasu. Wewnątrz powstałego z odcinków równoległoboku jest punkt O, znajduje się on w drugiej ćwiartce układu współrzędnych, a jego druga współrzędna ma wartość 6.

Przykład 5

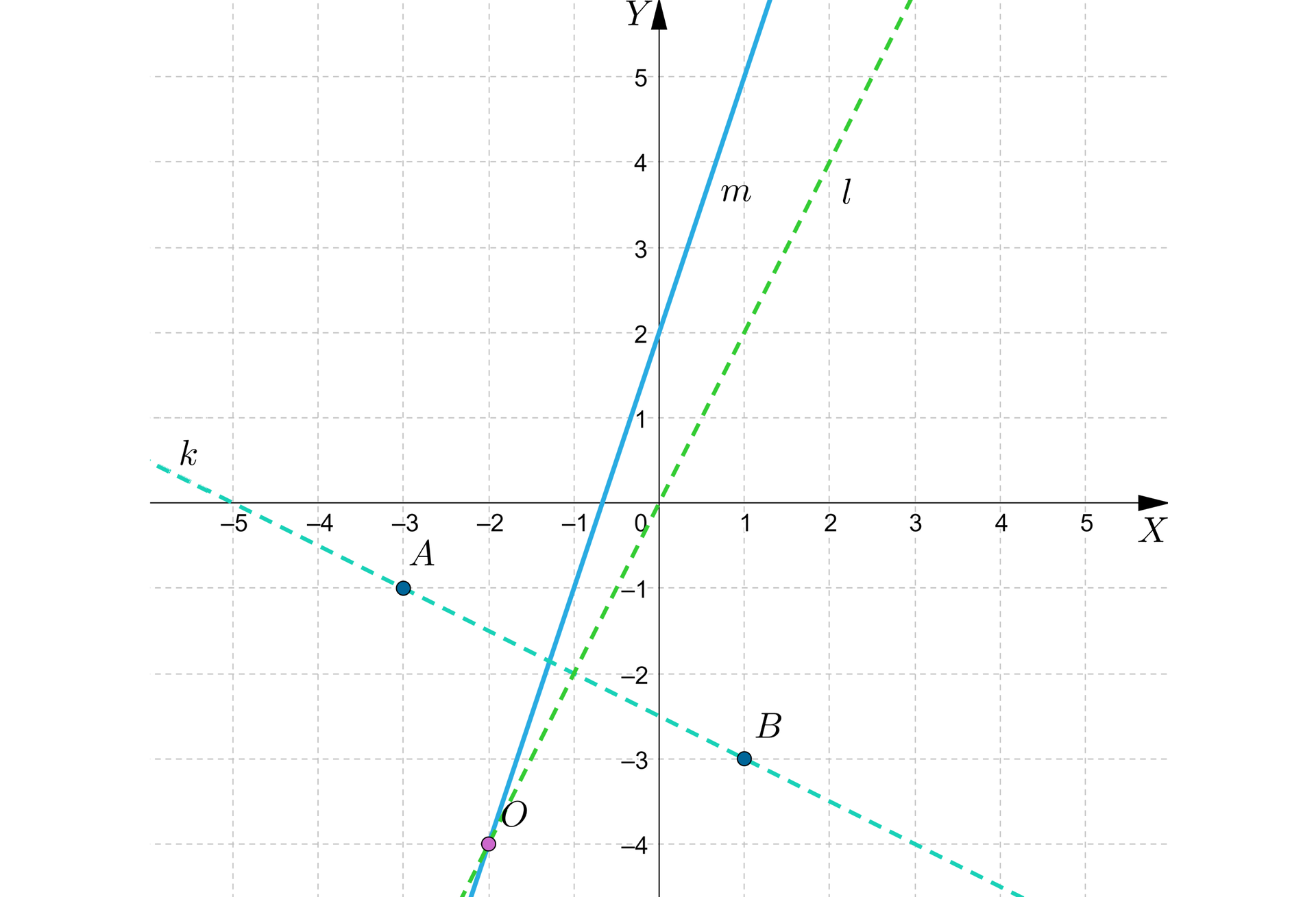
Rozważmy romb $A B C D$ , gdzie $A = (- 2, - 3)$ i $B = (3, - \frac{1}{2})$ . Wiedząc, że jedna z przekątnych rombu jest zawarta w prostej o równaniu $y = \frac{4}{3} x - \frac{1}{3}$ wyznaczymy współrzędne punktów $C$ i $D$ oraz środek symetrii tego rombu.

Rozwiązanie:

Zauważmy, że punkt $A$ leży na prostej $k$ danej równaniem $y = \frac{4}{3} x - \frac{1}{3}$ , ponieważ spełniona jest równość $- 3 = \frac{4}{3} \cdot (- 2) - \frac{1}{3}$ .

położenie przekątnych w rombie

Własność: położenie przekątnych w rombie

Przekątne w rombie przecinają się pod kątem prostym, punkt przecięcia przekątnych dzieli każdą z nich na pół.

Środek symetrii rombu (punkt przecięcia przekątnych) jest w tym przypadku punktem przecięcia prostej $k$ z prostą $l$ , która jest do niej prostopadła i przechodzi przez punkt $B$ .

Niech prosta $l$ określona równaniem $y = a_{2} x + b_{2}$ będzie prostą prostopadłą do prostej $k$ o równaniu $y = \frac{4}{3} x - \frac{1}{3}$ .

Z warunku prostopadłości prostych $a_{2} = - \frac{1}{a_{1}}$ . Ponieważ $a_{1} = \frac{4}{3}$ , więc $a_{2} = - \frac{1}{(\frac{4}{3})} = - \frac{3}{4}$ .

Zatem prosta $l$ przyjmuje postać $y = - \frac{3}{4} x + b_{2}$ .

Ponieważ prosta $l$ przechodzi przez punkt $B = (3, - \frac{1}{2})$ , możemy wyznaczyć $b_{2}$ .

Podstawiając współrzędne tego punktu do równania prostej $l$ otrzymujemy $- \frac{1}{2} = - \frac{3}{4} \cdot 3 + b_{2}$ , stąd $b_{2} = \frac{7}{4}$ . Ostatecznie otrzymujemy równanie prostej $y = - \frac{3}{4} x + \frac{7}{4}$ .

R6rTeNZ9QCMEY

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i osią y od minus 4 do pięciu. Na płaszczyźnie znajdują się 2 punkty A i B oraz dwie proste l i k. Współrzędne punktu A: początek nawiasu, minus 2, minus 3, zamknięcie nawiasu, punkt B znajduje się w czwartej ćwiartce układu współrzędnych, a jego pierwsza współrzędna jest równa 3. Ukośna prosta l namalowana linią przerywaną przechodzi przez punkt początek nawiasu, minus 3, 4, zamknięcie nawiasu oraz punkt początek nawiasu, 1, 1, zamknięcie nawiasu. Prosta l przechodzi przez punkt B. Ukośna prosta k przechodzi przez punkt początek nawiasu, 4, 5, zamknięcie nawiasu oraz punkt początek nawiasu, 1, 1, zamknięcie nawiasu.. Prosta k przechodzi przez punkt A. Proste l i k przecinają się w punkcie: początek nawiasu, 1, 1, zamknięcie nawiasu.

Punkt przecięcia prostej $k$ z prostą $l$ jest środkiem symetrii rombu, musimy rozwiązać układ równań:

$\{\begin{cases} y = \frac{4}{3} x - \frac{1}{3} \\ y = - \frac{3}{4} x + \frac{7}{4} \end{cases}$

Podstawiając stronami otrzymujemy $\frac{4}{3} x - \frac{1}{3} = - \frac{3}{4} x + \frac{7}{4}$ , a dalej $\frac{4}{3} x + \frac{3}{4} x = \frac{1}{3} + \frac{7}{4}$ . Po wykonaniu działań otrzymujemy $\frac{25}{12} x = \frac{25}{12}$ , a w rezultacie $x = 1$ .

Korzystając z pierwszego równania otrzymujemy $y = \frac{4}{3} \cdot 1 - \frac{1}{3}$ , a stąd $y = 1$ .

Otrzymaliśmy tym samym współrzędne punktu $O = (1, 1)$ , który jest środkiem symetrii danego rombu.

Wyznaczamy współrzędne pozostałych dwóch wierzchołków rombu, punktów $C$ i $D$ .

Z poznanych własności rombu wiemy, że punkt $O$ jest środkiem odcinka $A C$ . Znając współrzędne punktów $O = (1, 1)$ oraz $A = (- 2, - 3)$ otrzymujemy:

$x_{0} = \frac{x_{A} + x_{C}}{2}$ , a następnie $2 \cdot x_{0} = x_{A} + x_{C}$ . Otrzymujemy w ten sposób $x_{C} = 2 \cdot x_{0} - x_{A}$ .

Podobnie $y_{0} = \frac{y_{A} + y_{C}}{2}$ , następnie $2 \cdot y_{0} = y_{A} + y_{C}$ , a w rezultacie $y_{C} = 2 \cdot y_{0} - y_{A}$ .

Wykorzystując wyprowadzone równości otrzymujemy: $x_{C} = 2 \cdot 1 + 2 = 4$ i $y_{C} = 2 \cdot 1 + 3 = 5$ .

Wyznaczyliśmy tym samym współrzędne wierzchołka $C = (4, 5)$ .

Wykorzystując ponownie własności rombu, wiemy, że punkt $O$ jest środkiem odcinka $D B$ . Znając współrzędne punktów $O = (1, 1)$ , $B = (3, - \frac{1}{2})$ otrzymujemy:

$x_{0} = \frac{x_{D} + x_{B}}{2}$ , po przekształceniu $2 \cdot x_{0} = x_{D} + x_{B}$ , a w rezultacie $x_{D} = 2 \cdot x_{0} - x_{B}$ .

Podobnie, dla $y_{0} = \frac{y_{D} + y_{B}}{2}$ otrzymujemy $2 \cdot y_{0} = y_{D} + y_{B}$ , a w rezultacie $y_{D} = 2 \cdot y_{0} - y_{B}$ .

Wykorzystując wyprowadzone równości otrzymujemy: $x_{D} = 2 \cdot 1 - 3 = - 1$ i $y_{D} = 2 \cdot 1 + \frac{1}{2} = \frac{5}{2}$ .

Otrzymaliśmy w ten sposób współrzędne punktu $D = (- 1, \frac{5}{2})$ .

RB5lbu24sBjkp

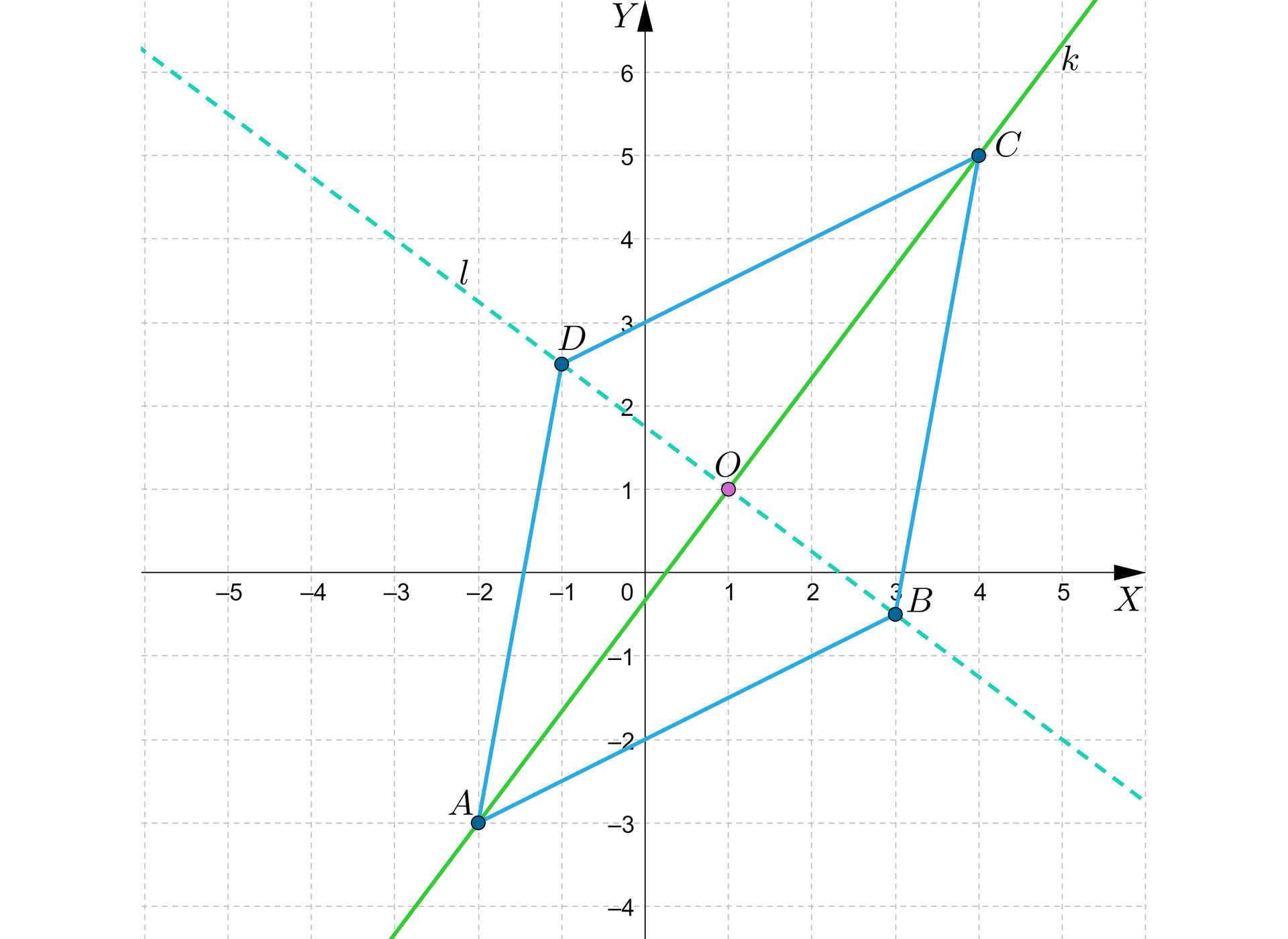
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i osią y od minus 4 do pięciu. Na płaszczyźnie znajdują się 4 punkty A, B, C, D, połączone ze sobą odcinkami oraz punkt O znajdujący się wewnątrz powstałego z odcinków równoległoboku. Na płaszczyźnie narysowane są również dwie proste. Ukośna prosta l namalowana linią przerywaną przechodzi przez punkt początek nawiasu, minus 3, 4, zamknięcie nawiasu oraz punkt początek nawiasu, 1, 1, zamknięcie nawiasu. Ukośna prosta k przechodzi przez punkt początek nawiasu, 4, 5, zamknięcie nawiasu oraz punkt początek nawiasu, 1, 1, zamknięcie nawiasu. Proste l i k przecinają się w punkcie: początek nawiasu, 1, 1, zamknięcie nawiasu. Punkt przecięcia prostych oznaczony jest literą O. Na prostej l znajdują się 2 punkty: punkt D o współrzędnej x równej minus 1 i punkt B o współrzędnej x równej 3. Na prostej k znajdują się punkty A i C. Punkt A ma współrzędne: początek nawiasu, minus 2, minus 3, zamknięcie nawiasu, Punkt C ma współrzędne: początek nawiasu, 4, 5, koniec nawiasu. Punkty A, B, C oraz D połączone są odcinkami i tworzą równoległobok.

Środkiem symetrii rombu jest punkt $O = (1, 1)$ , pozostałe wierzchołki to: $C = (4, 5)$ , $D = (- 1, \frac{5}{2})$ .

Słownik

środek symetrii figury

punkt $O$ nazywamy środkiem symetrii figury, jeśli symetria o środku $O$ przekształca tę figurę na nią samą

Wprowadzenie

Animacja

Słownik