Rozszerzanie i skracanie ułamków zwykłych
Równość ułamków

Film dostępny na portalu epodreczniki.pl
Animacja
Na każdym talerzu znajduje się taka sama część pizzy. Ułamki opisujące te części pizzy są równe.

Film dostępny na portalu epodreczniki.pl
Animacja
Rozszerzanie ułamków
Zauważ, że jeśli licznik i mianownik ułamka pomnożymy przez , to otrzymamy równy mu ułamek .

Film dostępny na portalu epodreczniki.pl
Animacja
Jeśli pomnożymy licznik i mianownik ułamka przez tę samą liczbę, różną od zera, to mówimy, że rozszerzyliśmy ułamek, a wartość ułamka się nie zmieni.
Podane ułamki rozszerz przez .
Rozszerz podane ułamki przez .
Uzupełnij.
Uzupełnij.
Skracanie ułamków

Film dostępny na portalu epodreczniki.pl
Animacja
Jeśli licznik i mianownik ułamka podzielimy przez tę samą liczbę, różną od zera, to wartość ułamka nie zmieni się. Mówimy, że skróciliśmy ułamek.
Na przykład
Skracając ułamek przez , otrzymujemy .

Skróć podane ułamki.
a) przez
b) przez
Uzupełnij brakujące liczniki i mianowniki tak, aby równości były prawdziwe.
a)
b)
Ułamki nieskracalne
Skróć ułamek przez największą możliwą liczbę.
Nieraz trudno jest znaleźć największą liczbę, przez którą można skrócić dany ułamek. Na przykład, aby skrócić ułamek możemy postąpić tak:
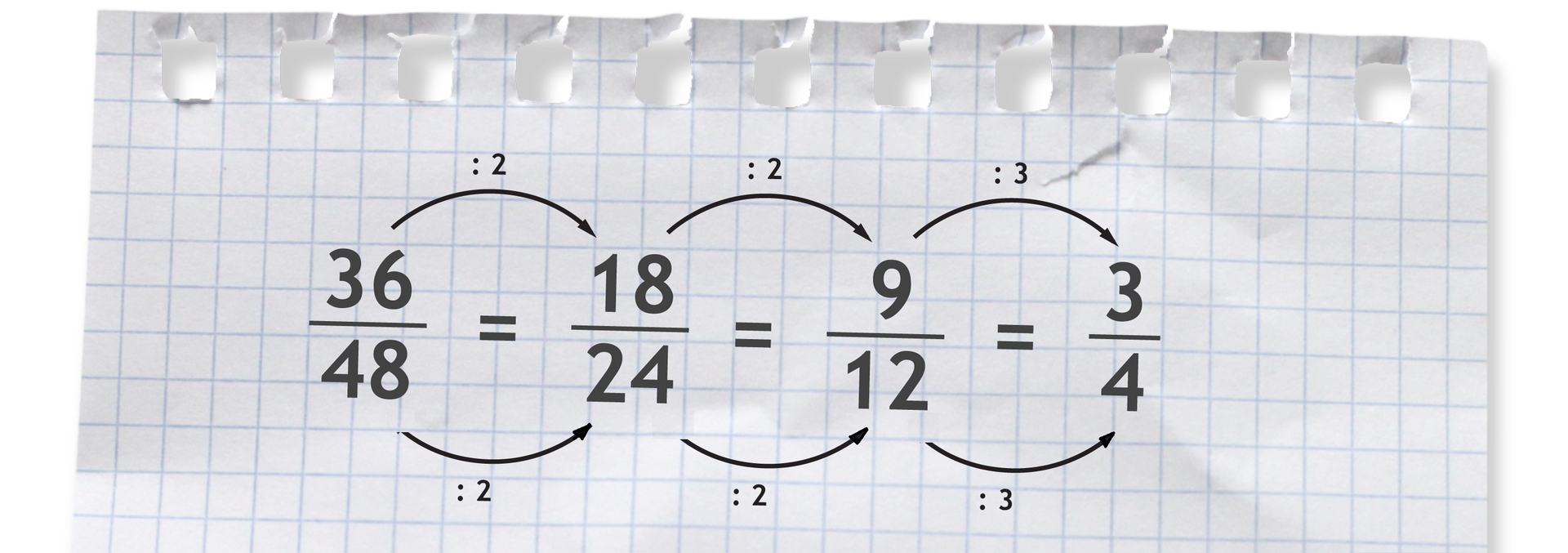
Ułamka nie można już skrócić.
Ułamek, którego nie można skrócić nazywamy ułamkiem nieskracalnym.
Podane ułamki zapisz w postaci ułamka nieskracalnego.
Podane ułamki zapisz w postaci ułamka nieskracalnego.
Przeciągnij i upuść.
, , ,
............
............
............
............
Połącz w pary tak, aby brakującym elementom ułamka przyporządkować odpowiednią liczbę.
<span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, sześćdziesiąt, mianownik, □, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mn>60</mn><mo>□</mo></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, dwadzieścia cztery, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>24</mn></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, szesnaście, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>16</mn></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, sto, mianownik, □, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mn>100</mn><mo>□</mo></mfrac></math></span>, <span aria-label="początek ułamka, pięć, mianownik, osiem, koniec ułamka, równa się, początek ułamka, □, mianownik, czterdzieści osiem, koniec ułamka" role="math"><math><mfrac><mn>5</mn><mn>8</mn></mfrac><mo>=</mo><mfrac><mo>□</mo><mn>48</mn></mfrac></math></span>
| 10 | |
| 15 | |
| 30 | |
| 96 | |
| 160 |
Jeśli ułamek rozszerzymy przez lub przez , to otrzymamy ułamek, którego licznik i mianownik mają ciekawą własność. Jeżeli licznik przeczytamy od prawej do lewej strony, otrzymamy mianownik. Oczywiście ten sam efekt otrzymamy, gdy postąpimy podobnie z mianownikiem.
i
Znajdź inne ułamki, które mają tę samą własność.