Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

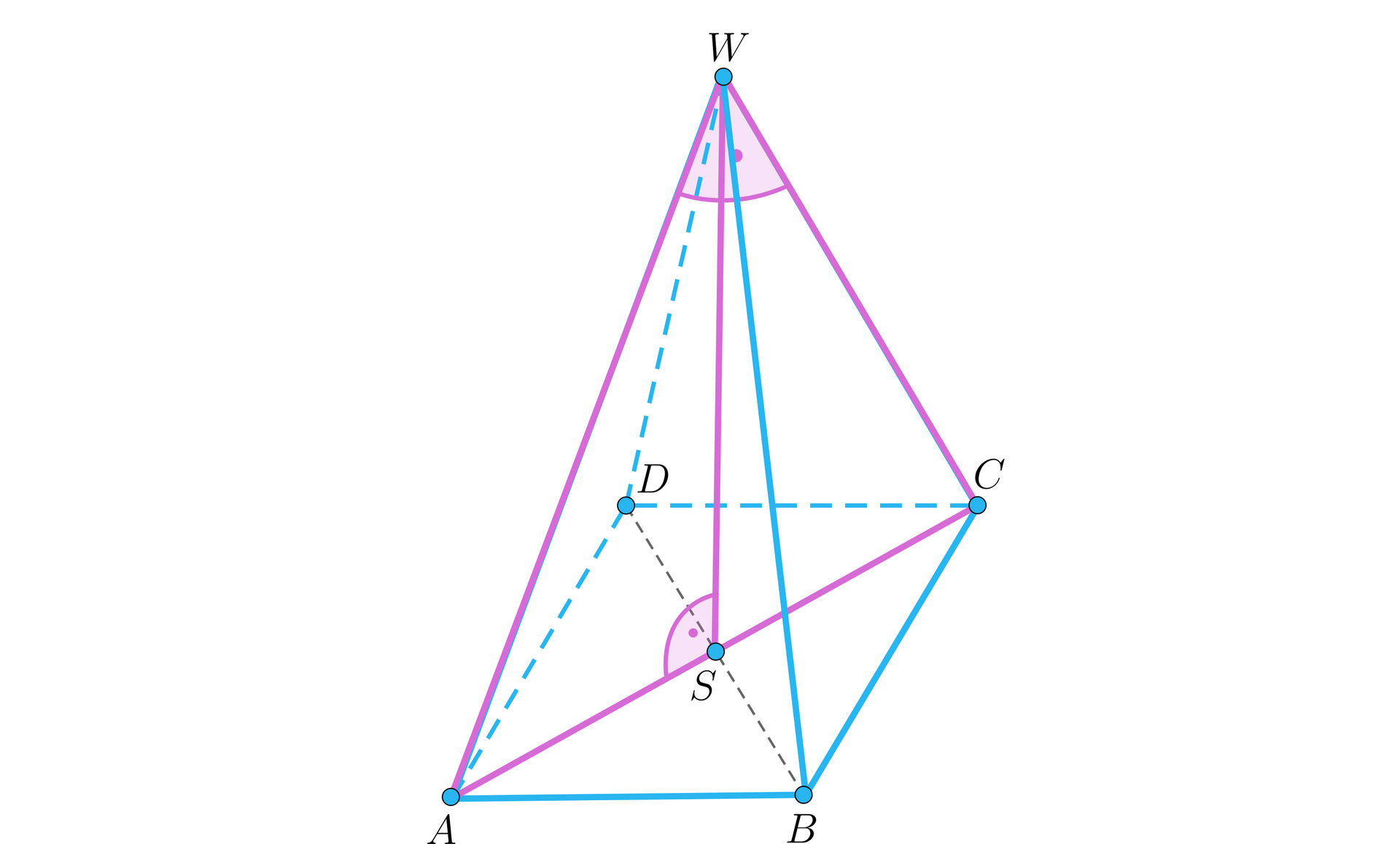
Na rysunku dany jest ostrosłup prawidłowy czworokątny.

R1R03E8TMCT2F

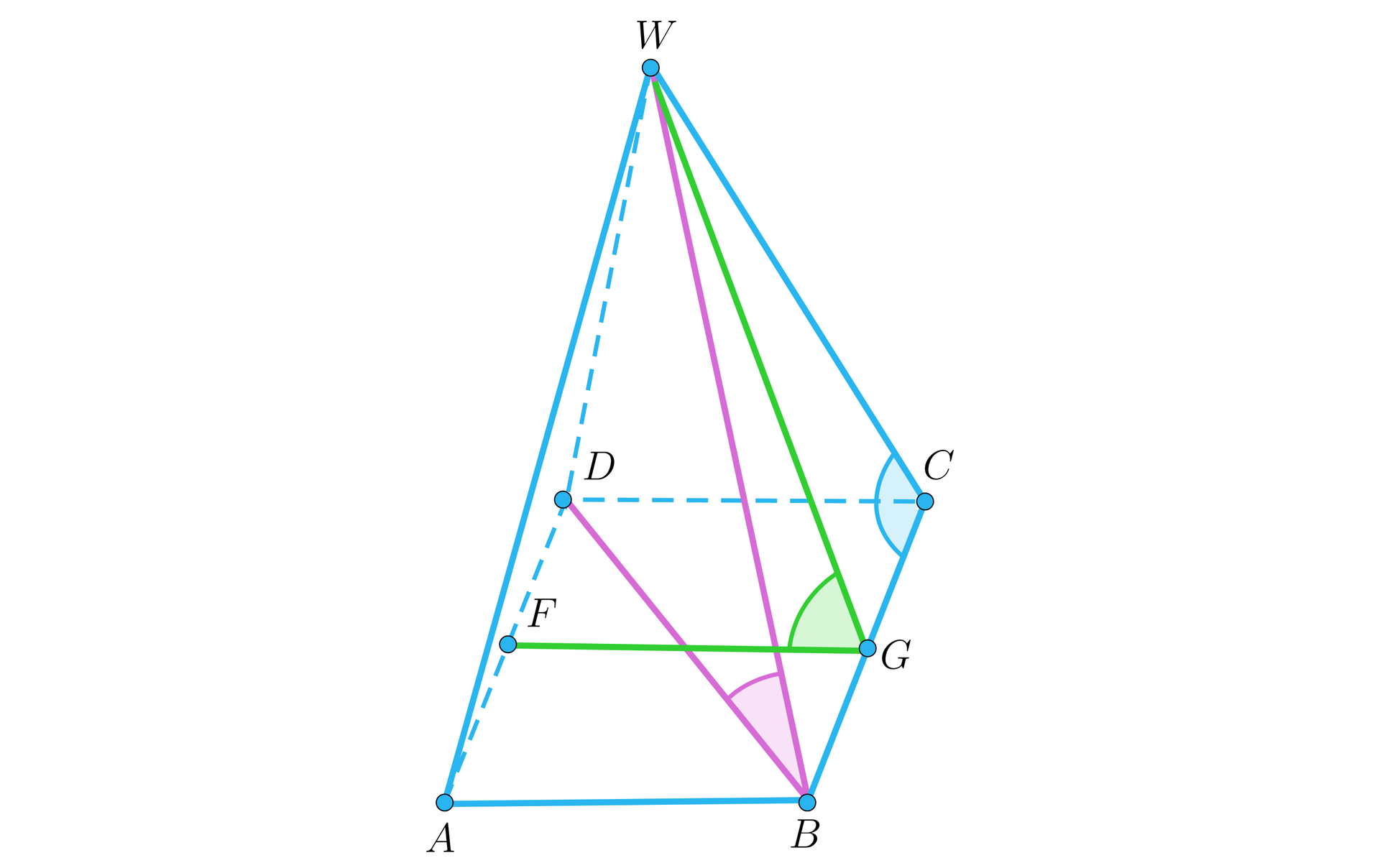
Ilustracja przedstawia ostrosłup prawidłowy czworokątny A B C D W. Z wierzchołka W poprowadzono wysokość ściany bocznej W B C upuszczonej na środek odcinka B C w punkcie G. Punkt G połączono z punktem F znajdującym się na środku przeciwległego odcinka A D. Zaznaczono kąt pomiędzy odcinkami W G i F G. Z wierzchołka B poprowadzono przekątną podstawy B D i tam także zaznaczono kąt pomiędzy odcinkami W B i B D.

R1GMeHQa32ygN

Który z wymienionych kątów jest kątem między krawędzią boczną i płaszczyzną podstawy? Zaznacz poprawną odpowiedź.

$∡ W B D$
$∡ W G F$
$∡ W C B$

Ćwiczenie 2

RzbbA1P3V4BoB

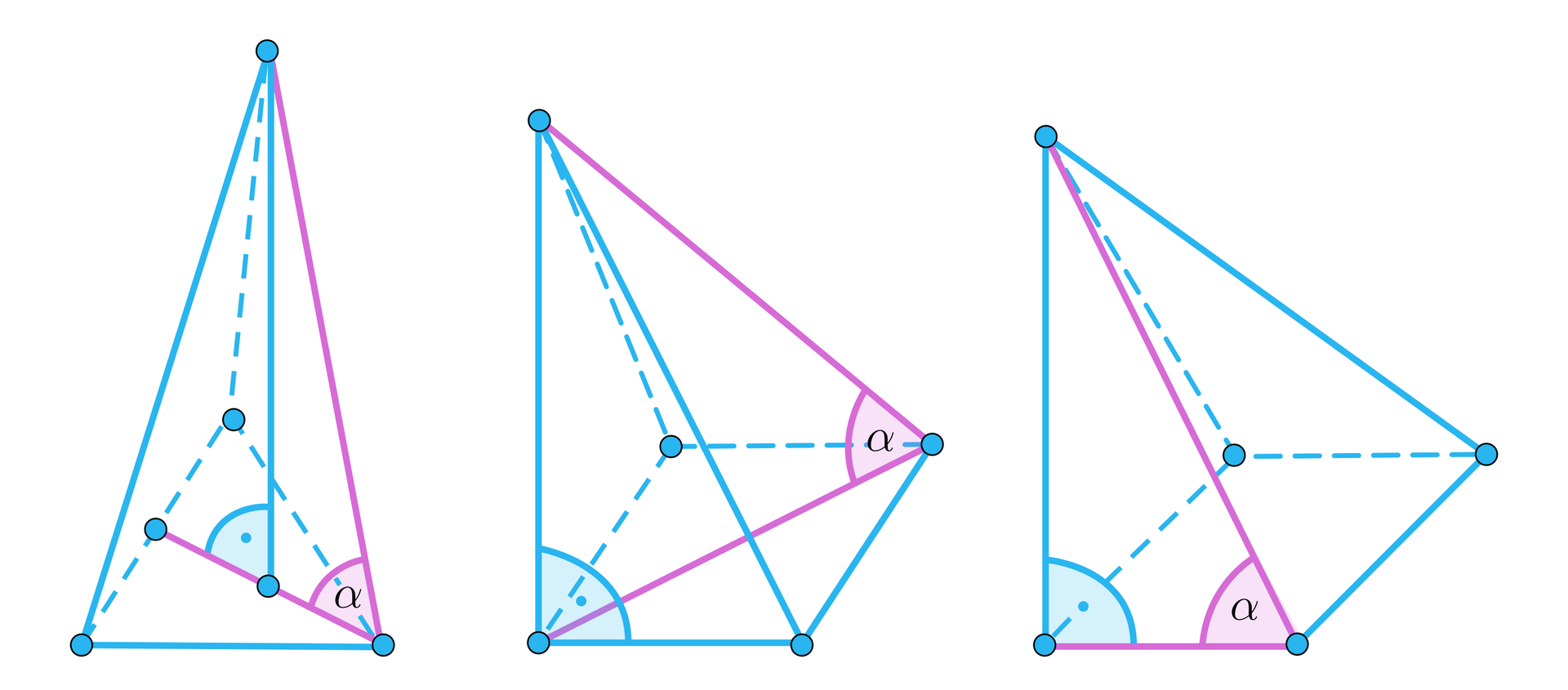
Grafika przedstawia trzy różne kąty w trzech różnych ostrosłupach. Ilustracja pierwsza przedstawia ostrosłup z narysowaną wysokością podstawy. Kąt alfa został zaznaczony pomiędzy wysokością podstawy a krawędzią ściany bocznej. Ilustracja druga przedstawia ostrosłup z narysowaną przekątną podstawy. Kąt alfa został zaznaczony pomiędzy przekątną podstawy a krawędzią boczną bryły. Ilustracja trzecia przedstawia ostrosłup z zaznaczonym kątem alfa pomiędzy krawędzią boczną bryły a krawędzią podstawy.

R1KUgJUiavoHV

Na których rysunkach zaznaczony kąt nie jest kątem między krawędzią boczną i płaszczyzną podstawy ostrosłupa? Zaznacz poprawną odpowiedź.

Tylko na rysunku 2.
Tylko na rysunku 1 oraz 2.
Tylko na rysunku 3.

RKraquUqJi32Q2

Ćwiczenie 3

Dostępne opcje do wyboru: krawędź boczna, odcinek, odcinek, krawędź boczna, odcinek, punkt, odcinek, prosta, prosta, prosta, prosta, punkt. Polecenie: Uzupełnij poniższy tekst wyrazami podanymi poniżej, aby otrzymać kompletny dowód twierdzenia. Rzutem prostokątnym prostej na płaszczyznę może być albo luka do uzupełnienia albo punkt. Jeżeli tym rzutem jest luka do uzupełnienia , to dana luka do uzupełnienia jest prostopadła do płaszczyzny. Wynika stąd, że rzutem prostokątnym krawędzi bocznej ostrosłupa na płaszczyznę jego podstawy może być albo luka do uzupełnienia albo punkt. Jeżeli tym rzutem jest luka do uzupełnienia , to dana luka do uzupełnienia jest prostopadła do płaszczyzny podstawy ostrosłupa. Ponieważ tylko jedna luka do uzupełnienia ostrosłupa może mieć taką własność, to prawdziwe jest twierdzenie:
"W każdym ostrosłupie

n

–kątnym rzutem prostokątnym co najmniej

n - 1

krawędzi bocznych na płaszczyznę podstawy są odcinki".

Uzupełnij poniższy tekst wyrazami podanymi poniżej, aby otrzymać kompletny dowód twierdzenia:

odcinek, krawędź boczna, prosta, prosta, odcinek, prosta, odcinek, punkt, prosta, krawędź boczna, punkt, odcinek

Rzutem prostokątnym prostej na płaszczyznę może być albo albo punkt. Jeżeli tym rzutem jest , to dana jest prostopadła do płaszczyzny. Wynika stąd, że rzutem prostokątnym krawędzi bocznej ostrosłupa na płaszczyznę jego podstawy może być albo albo punkt. Jeżeli tym rzutem jest , to dana jest prostopadła do płaszczyzny podstawy ostrosłupa. Ponieważ tylko jedna ostrosłupa może mieć taką własność, to prawdziwe jest twierdzenie:
"W każdym ostrosłupie $n$ –kątnym rzutem prostokątnym co najmniej $n - 1$ krawędzi bocznych na płaszczyznę podstawy są odcinki".

RmJAgRkTcKBIL2

Ćwiczenie 4

Zaznacz wszystkie poprawne odpowiedzi. Podstawą ostrosłupa jest prostokąt. Punkt przecięcia przekątnych podstawy jest spodkiem wysokości tego ostrosłupa. Wynika stąd, że:

Krawędzie boczne ostrosłupa są równej długości.
Krawędzie boczne ostrosłupa tworzą z podstawą równe kąty.
Ściany boczne ostrosłupa tworzą z podstawą równe kąty.

RfeD7faBVQWIq2

Ćwiczenie 5

Zaznacz poprawną odpowiedź. Punkt $S$ jest spodkiem wysokości ostrosłupa $A B C W$ , a krawędzie boczne $A W$ , $B W$ , $C W$ tworzą z podstawą kąty o równych miarach. Która własność musi być prawdziwa:

Punkt $S$ jest punktem przecięcia środkowych trójkąta $A B C$ .
Punkt $S$ jest środkiem okręgu wpisanego w trójkąt $A B C$ .
Punkt $S$ jest środkiem okręgu opisanego na trójkącie $A B C$ .

Ćwiczenie 6

W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy $a$ , wysokość ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem $45 °$ . Oblicz kąt nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny jego podstawy.

Oto szkic do zadania:

R1DbNRphuvEYh

Ilustracja przedstawia ostrosłup prawidłowy czworokątny A B C D W. Z wierzchołka W poprowadzono wysokość bryły padającej na środek podstawy w punkcie S. Z tego samego wierzchołka W poprowadzono również wysokość ściany bocznej upuszczonej na środek boku B C w punkcie E. Powstał nowy trójkąt prostokątny W S E z kątem prostym przy wierzchołku S oraz kątem alfa przy wierzchołku E. Zaznaczono również trójkąt S B W oraz kąt beta przy wierzchołku B.

Z trójkąta $W S E$ mamy:

$\frac{|W S|}{\frac{a}{2}} = tg 45 °$

$|W S| = \frac{a}{2}$

Z trójkąta $W S B$ mamy:

$\frac{|W S|}{\frac{a \sqrt{2}}{2}} = tg β$

$\frac{\frac{a}{2}}{\frac{a \sqrt{2}}{2}} = tg β$

$\frac{\sqrt{2}}{2} = tg β$

$35 ° \approx β$ .

Ćwiczenie 7

Podstawą ostrosłupa jest romb o boku długości $24$ i kącie rozwartym $120 °$ . Przeciwległe krawędzie boczne ostrosłupa są parami równe. Krótsza krawędź boczna jest dwa razy dłuższa od krawędzi podstawy bryły. Oblicz cosinusy kątów nachylenia krawędzi bocznych tego ostrosłupa do płaszczyzny jego podstawy.

Rozpatrzmy ostrosłup przyjmując następujące oznaczenia jego wierzchołków:

R62vNNPOMoNLd

Ilustracja przedstawia ostrosłup A B C D W z rombem w podstawie o długości boków równej dwadzieścia cztery. Z wierzchołka W poprowadzono wysokość bryły padającej na środek podstawy w punkcie S. Na ilustracji znajdują się także dwie przekątne podstawy, przekątna A C oraz przekątna B D. Odcinek A C ma długość dwadzieścia cztery pierwiastki z trzech, natomiast odcinek B D ma długość dwadzieścia cztery.

Ponieważ kąt rozwarty rombu jest równy $120 °$ , to romb ten jest zbudowany z dwóch trójkątów równobocznych o boku $24$ . Zatem krótsza przekątna rombu ma również długość $24$ a dłuższa przekątna rombu ma długość $24 \sqrt{3}$ . Jednocześnie z warunków zadania wynika, że krótsza krawędź boczna ostrosłupa ma długość $48$ .

Z twierdzenia Pitagorasa w trójkącie $W S B$ wyznaczamy wysokość ostrosłupa $|W S| = 12 \sqrt{15}$ .

Ponownie z tego twierdzenia w trójkącie $W S C$ wyznaczamy długość dłuższej krawędzi bocznej ostrosłupa $|W C| = 36 \sqrt{2}$ .

Ostatecznie cosinusy kątów nachylenia krawędzi bocznych do płaszczyzny podstawy są równe odpowiednio:

$\cos ∡ W B S = \frac{|B S|}{|W B|}$

$\cos ∡ W B S = \frac{12}{48}$

$\cos ∡ W B S = \frac{1}{4}$

Analogicznie:

$\cos ∡ W C S = \frac{|C S|}{|W C|}$

$\cos ∡ W C S = \frac{12 \sqrt{3}}{36 \sqrt{2}}$

$\cos ∡ W C S = \frac{\sqrt{6}}{6}$ .

Ćwiczenie 8

W ostrosłupie prawidłowym czworokątnym $A B C D W$ o podstawie $A B C D$ , trójkąt $A W C$ jest prostokątny. Udowodnij, że wszystkie krawędzie ostrosłupa są takiej samej długości i oblicz cosinus kąta nachylenia wysokości ściany bocznej do płaszczyzny podstawy ostrosłupa.

RTP0Bdl0Z2EIo

Skoro ostrosłup jest prawidłowy, to jego krawędzie boczne są równej długości. Przyjmijmy oznaczenie $a$ – długość krawędzi bocznej ostrosłupa. Wówczas z założenia zadania przekątna podstawy ostrosłupa ma długość $a \sqrt{2}$ . Konsekwentnie wykorzystując fakt, że podstawa ostrosłupa jest kwadratem, krawędź podstawy musi mieć długość $a$ . Oznacza to, że wszystkie krawędzie naszego ostrosłupa są równe.

Ściana boczna ostrosłupa jest zatem trójkątem równobocznym o wysokości $\frac{a \sqrt{3}}{2}$ . Cosinus kąta nachylenia tej wysokości do płaszczyzny podstawy ostrosłupa jest zatem równy: $\cos α = \frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}} = \frac{\sqrt{3}}{3}$ .

Animacja 3D

Dla nauczyciela