Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na rysunku przedstawiony jest wykres funkcji $y = f (x)$ . Dziedziną funkcji jest zbiór:

RoBsn0S4Ho8Q5

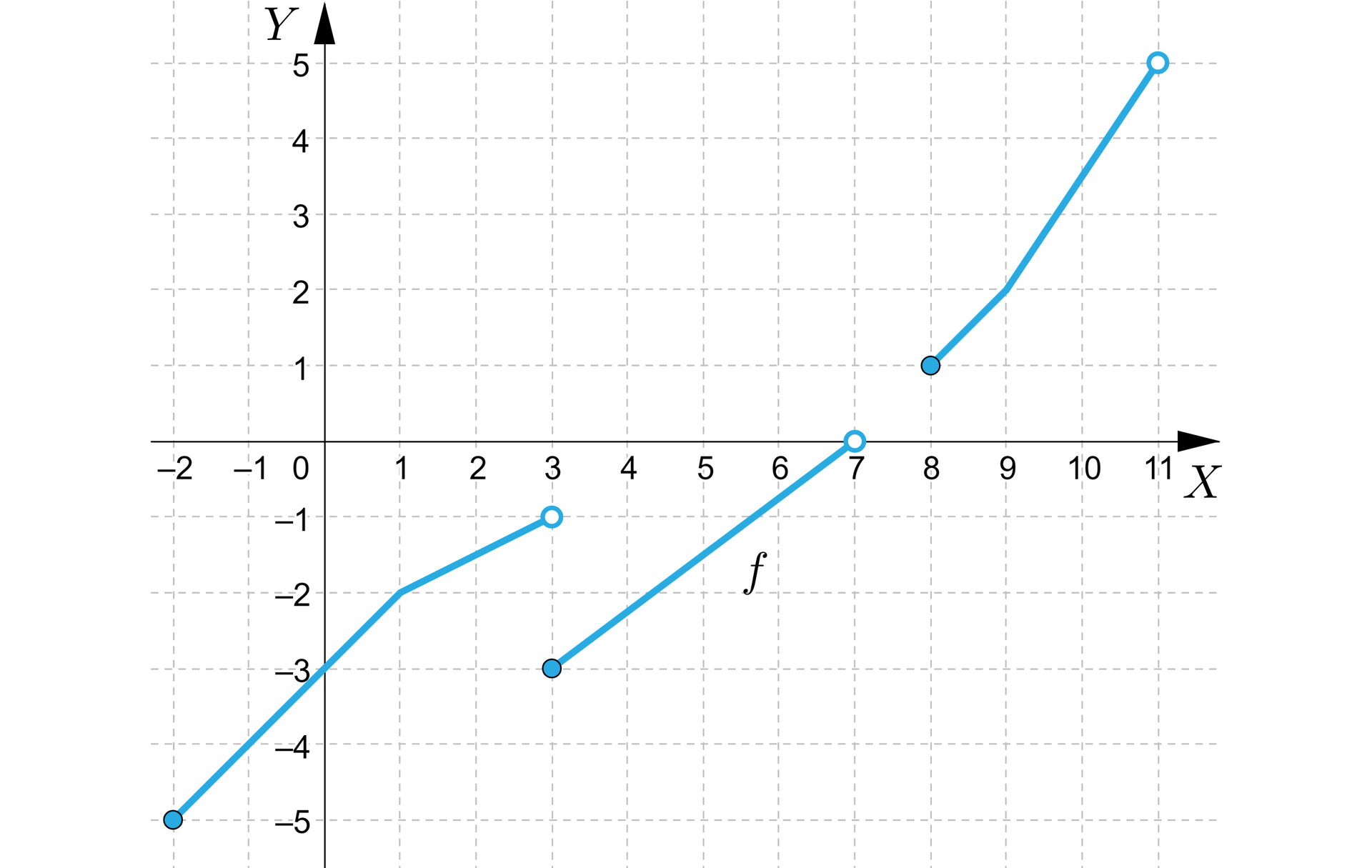
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 11 i pionową osią y od minus 5 do pięć. W układzie zaznaczono wykres f, który składa się z trzech fragmentów. Pierwsza część pojawia się w zamalowanym puncie o współrzędnych nawias minus dwa średnik minus pięć zamknięcie nawiasu, biegnie on ukośnie przecinając oś y w punkcie nawias zero średnik minus trzy zamknięcie nawiasu, do punktu nawias jeden średnik minus dwa zamknięcie nawiasu, gdzie zmienia swoje nachylenie i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias trzy średnik minus jeden zamknięcie nawiasu. Druga część zaczyna się w zamalowanym punkcie o współrzędnych nawias trzy średnik minus trzy zamknięcie nawiasu i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias siedem średnik zero zamknięcie nawiasu. Trzecia część rozpoczyna się w zamalowanym punkcie nawias osiem średnik jeden zamknięcie nawiasu i biegnie do punktu nawias dziewięć średnik dwa zamknięcie nawiasu, tam zmienia swoje nachylenie i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias jedenaście średnik pięć zamknięcie nawiasu.

RwmN7fPNGvBU6

Zaznacz poprawną odpowiedź.

$"⟨"- 2, 11"⟩"$
$"⟨"- 2, 7")" \cup "⟨"8, 11")"$
$"⟨"- 1, 3")" \cup "⟨"3, 11")"$
$"⟨"- 1, 7")" \cup "⟨"8, 11"⟩"$

Ćwiczenie 2

Na rysunku przedstawiony jest wykres funkcji $y = f (x)$ . Zbiorem wartości tej funkcji jest:

R1RVm0cIR1bbF

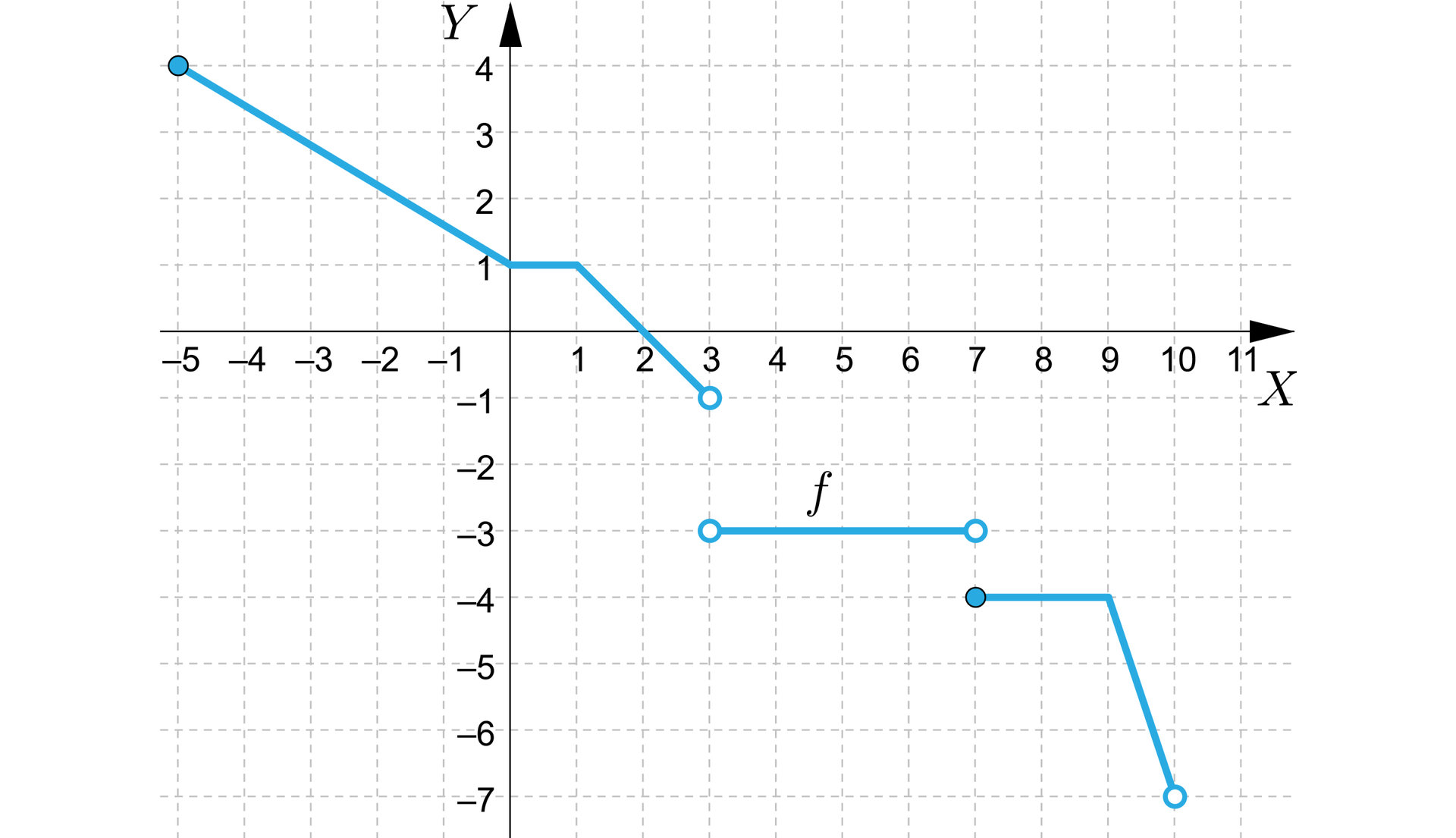
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 11 i pionową osią y od minus 7 do cztery. W układzie zaznaczono wykres f, który składa się z trzech fragmentów. Pierwsza część pojawia się w zamalowanym puncie o współrzędnych nawias minus pięć średnik cztery zamknięcie nawiasu, biegnie on ukośnie przecinając oś y w punkcie nawias zero średnik jeden zamknięcie nawiasu, tu zmienia swój bieg i biegnie poziomo do punktu nawias jeden średnik jeden zamknięcie nawiasu, gdzie zmienia swoje nachylenie i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias trzy średnik minus jeden zamknięcie nawiasu. Druga część zaczyna się w niezamalowanym punkcie o współrzędnych nawias trzy średnik minus trzy zamknięcie nawiasu i biegnie poziomo do niezamalowanego punktu o współrzędnych nawias siedem średnik minus trzy zamknięcie nawiasu. Trzecia część rozpoczyna się w zamalowanym punkcie nawias siedem średnik minus cztery zamknięcie nawiasu i biegnie poziomo do punktu nawias dziewięć średnik minus cztery zamknięcie nawiasu, tam zmienia swoje nachylenie i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias dziesięć średnik minus siedem zamknięcie nawiasu.

R1IwV42SoMHij

Zaznacz poprawną odpowiedź.

$"("- 7, 4"⟩"$
$(- 7, - 4) \cup (- 1, 4)$
$"("- 7, - 4"⟩" \cup "{"- 3"}" \cup "("- 1, 4"⟩"$
$"⟨"- 7, - 4")" \cup "{"- 3"}" \cup "("- 1, 4"⟩"$

Ćwiczenie 3

Na rysunku przedstawiono wykres funkcji $f$ .

R1HcWBL6Btb1g

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 10 i pionową osią y od minus 5 do pięć. W układzie zaznaczono wykres f, który jest krzywą zaczyna się on w zamalowanym puncie o współrzędnych nawias minus jeden średnik minus pięć zamknięcie nawiasu, dalej biegnie on ukośnie przecinając oś y w punkcie nawias zero średnik minus cztery zamknięcie nawiasu do punktu nawias jeden średnik minus trzy zamknięcie nawiasu, gdzie zmienia swoje nachylenie i biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias pięć średnik minus jeden zamknięcie nawiasu. Dalej wykres biegnie po łuku do punktu nawias siedem średnik zero zamknięcie nawiasu. Dalej biegnie on ukośnie do niezamalowanego punktu o współrzędnych nawias dziesięć średnik pięć zamknięcie nawiasu.

R1ONTL62xvdgq

Łączenie par. Rozstrzygnij, czy zdanie jest prawdziwe czy fałszywe, zaznaczając odpowiednie pole.. Funkcja jest rosnąca w całej dziedzinie, więc jest monotoniczna.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest różnowartościowa.. Możliwe odpowiedzi: Prawda, Fałsz. Wartość najmniejsza

y_{\min} = - 5

dla

x = - 1

.. Możliwe odpowiedzi: Prawda, Fałsz. Wartość największa funkcji

y_{\max} = 5

dla

x = 10

.. Możliwe odpowiedzi: Prawda, Fałsz

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

Zdanie	Prawda	Fałsz
Funkcja jest rosnąca w całej dziedzinie, więc jest monotoniczna.	□	□
Funkcja jest różnowartościowa.	□	□
Wartość najmniejsza $y_{\min} = - 5$ dla $x = - 1$ .	□	□
Wartość największa funkcji $y_{\max} = 5$ dla $x = 10$ .	□	□

Ćwiczenie 4

R1KuSXdvCfr5l

RrG1JLP6vK0Su

Ćwiczenie 5

RRiJchEMDCekk

R1HXHc1OqkbzN

Ćwiczenie 6

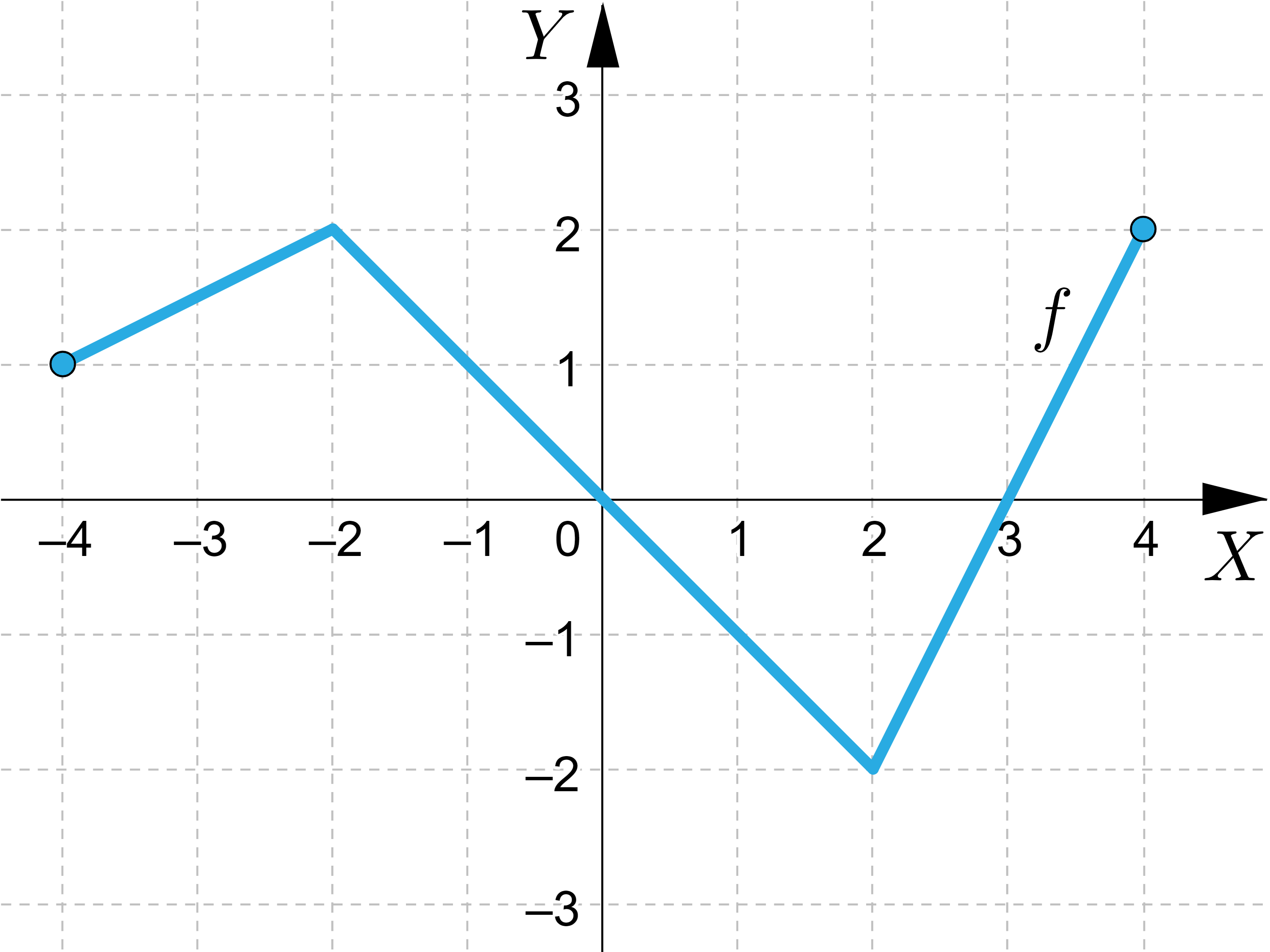
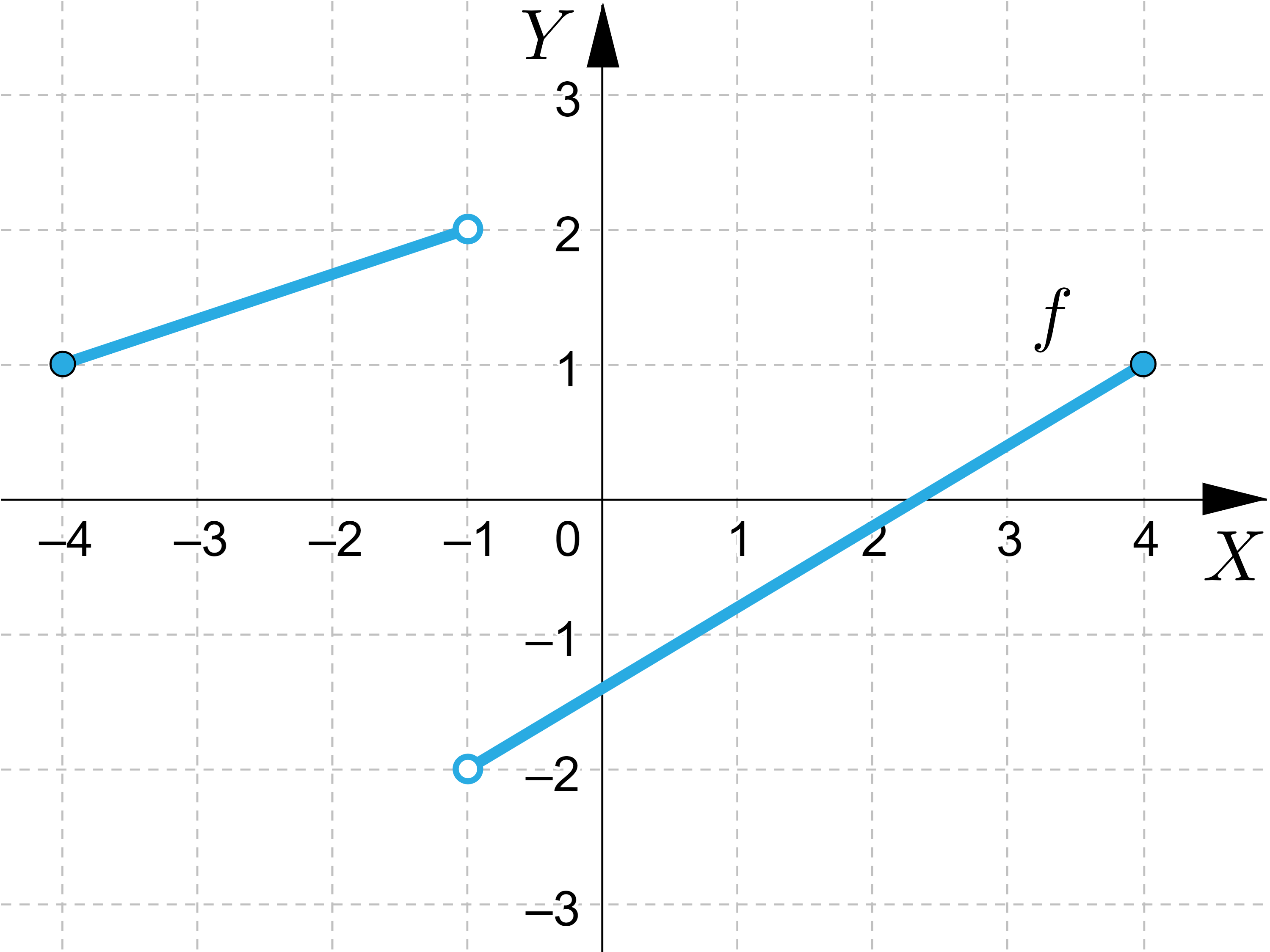
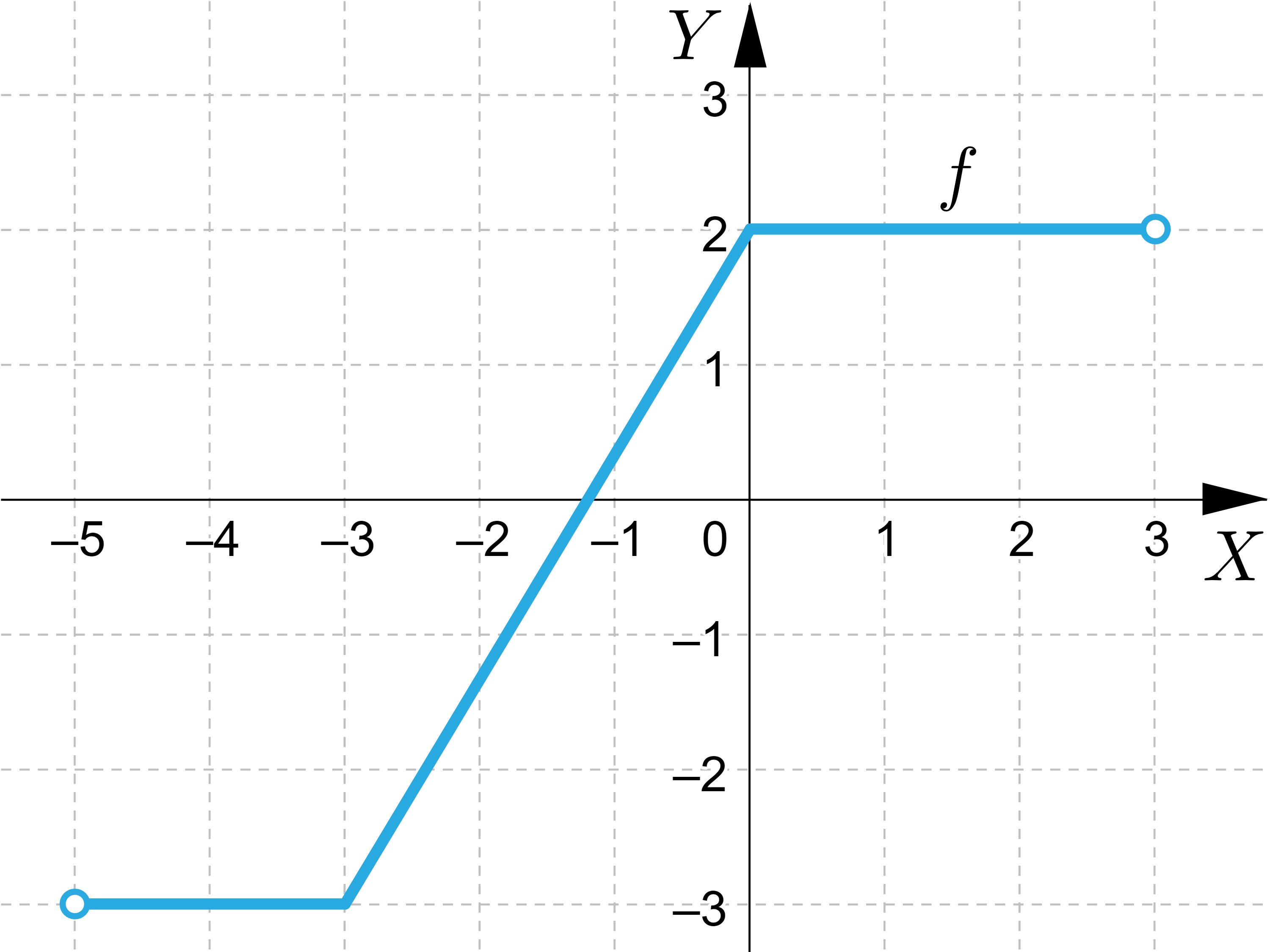
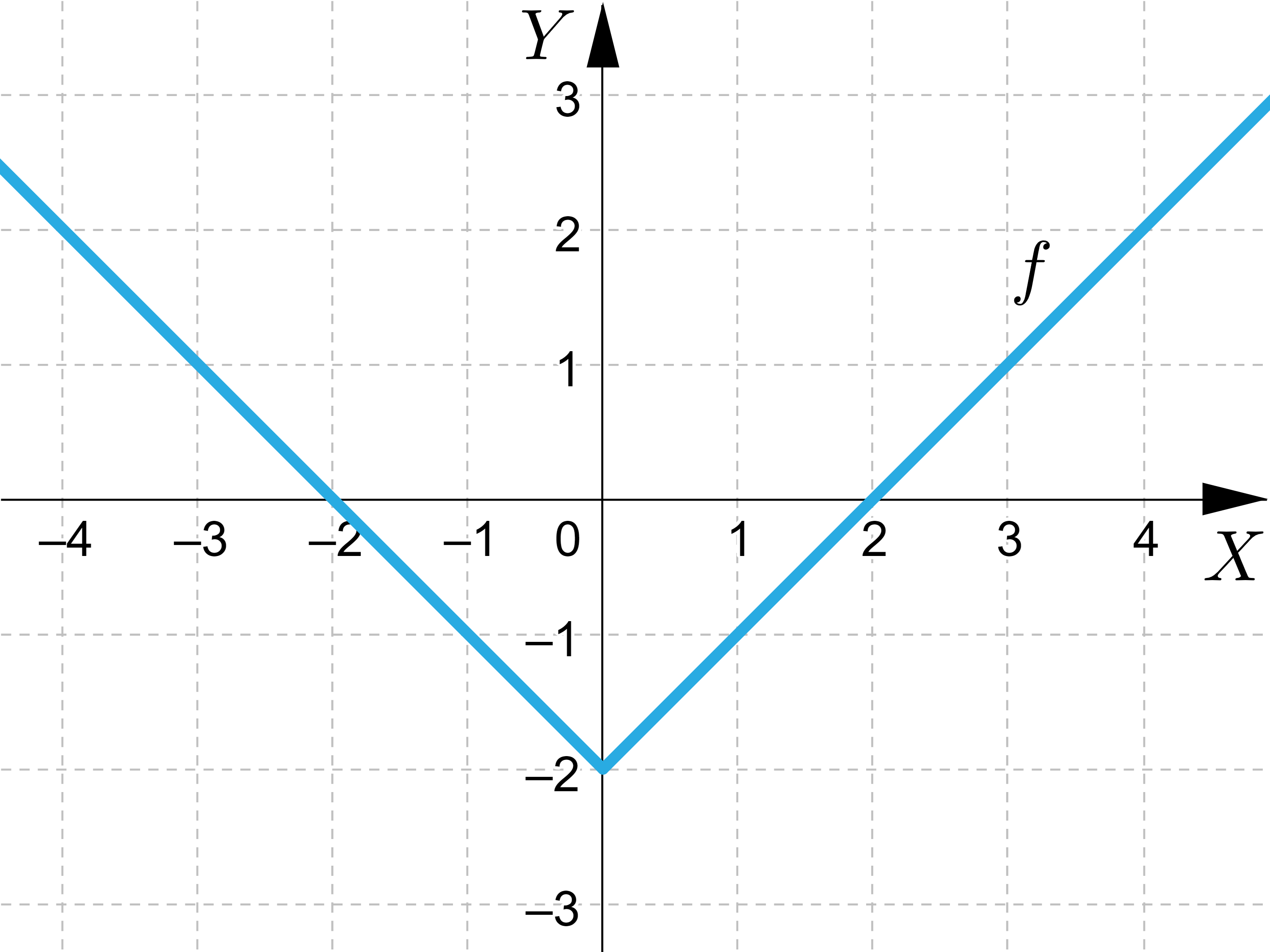
Na podstawie analizy przedstawionego na rysunku wykresu funkcji zaznacz poprawnie opisane własności funkcji:

R18YwB5wfQyY7

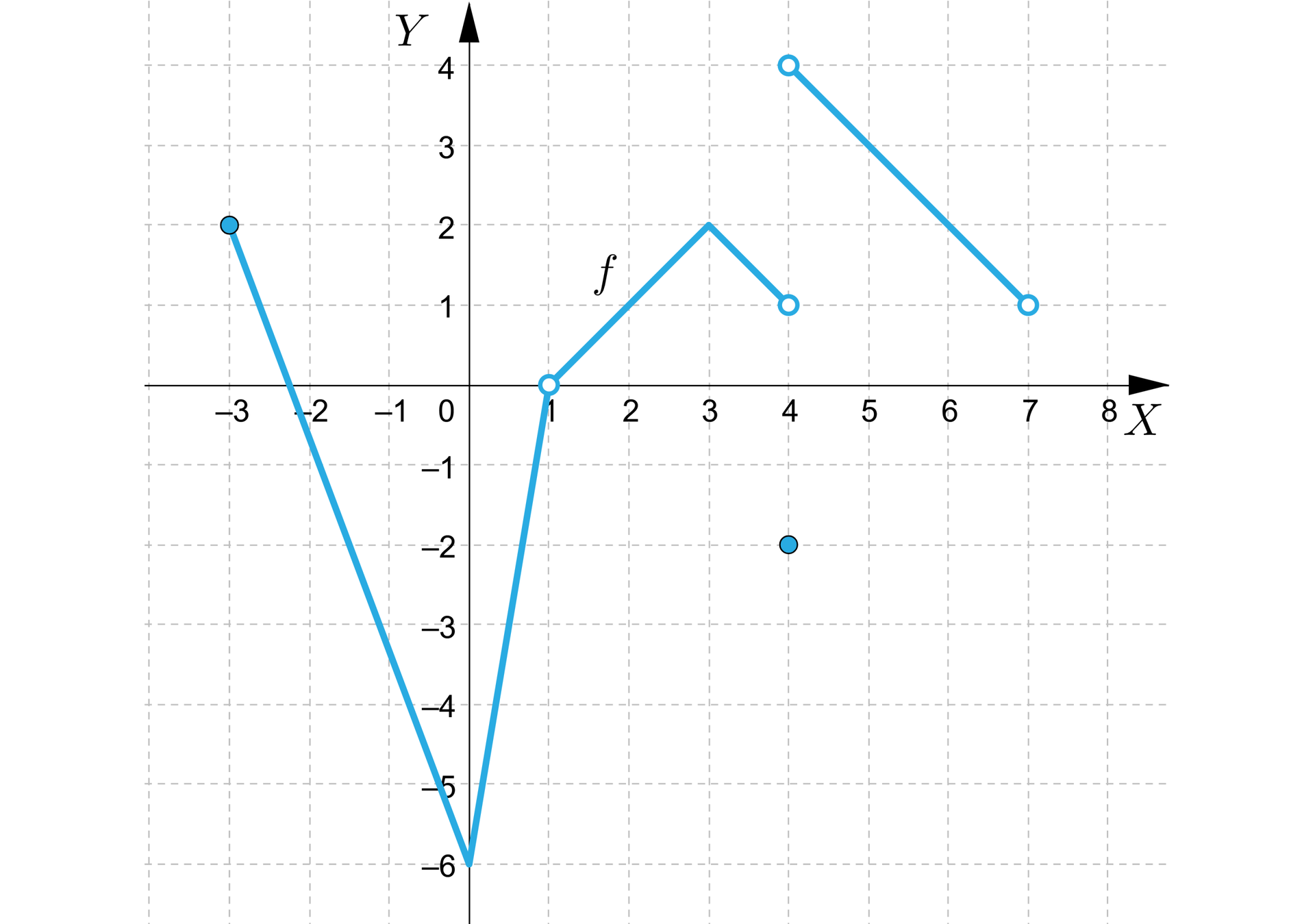
Ilustracja przedstawia układ współrzędnych z pozioma osią od minus 3 do 8 i pionową osią y od minus 6 do cztery. W układzie zaznaczono wykres funkcji f, który składa się z trzech części. Pierwsza część jest krzywą, która rozpoczyna się w zamalowanym punkcie nawiasu minus trzy średnik dwa zamknięcie nawiasu, skąd biegnie ukośnie do punktu nawias zero średnik minus sześć zamknięcie nawiasu, z tego punktu biegnie ukośnie do niezamalowanego punktu o współrzędnych nawias jeden średnik zero zamknięcie nawiasu. Dalej biegnie ukośnie do punktu nawias trzy średnik dwa zamknięcie nawiasu, skąd ukośnie biegnie do niezamalowanego punktu o współrzędnych nawias cztery średnik jeden zamknięcie nawiasu. Drugą częścią jest zamalowany punkt o współrzędnych nawias cztery średnik minus dwa zamknięcie nawiasu. Trzecia część rozpoczyna się w niezamalowanym punkcie o współrzędnych nawias cztery średnik cztery skąd biegnie ukośnie do niezamalowanego punktu nawias siedem średnik jeden zamknięcie nawiasu.

RGf5Y7TZwq93Z

Łączenie par. Wybierz prawda lub fałsz, zaznaczając odpowiednio przy każdym zdaniu.. Funkcja posiada dwa miejsca zerowe.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja nie przyjmuje wartości największej, wartość najmniejsza

y_{\min} = - 6

dla

x = 0

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest rosnąca tylko w przedziale

⟨0, 3⟩

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest malejąca w przedziałach:

⟨- 3, 0⟩

;

⟨3, 4)

;

(4, 7)

.. Możliwe odpowiedzi: Prawda, Fałsz.

f (x) = 0

dla

x = - 2,2

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest rosnąca w przedziałach:

⟨0, 1)

oraz

(1, 3⟩

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest różnowartościowa.. Możliwe odpowiedzi: Prawda, Fałsz

Zdanie	Prawda	Fałsz
Funkcja posiada dwa miejsca zerowe.	□	□
Funkcja nie przyjmuje wartości największej, wartość najmniejsza $y_{\min} = - 6$ dla $x = 0$ .	□	□
Funkcja jest rosnąca tylko w przedziale $"⟨"0, 3"⟩"$ .	□	□
Funkcja jest malejąca w przedziałach: $"⟨"- 3, 0"⟩"$ ; $"⟨"3, 4")"$ ; $(4, 7)$ .	□	□
$f (x) = 0$ dla $x = - 2,2$ .	□	□
Funkcja jest rosnąca w przedziałach: $"⟨"0, 1")"$ oraz $"("1, 3"⟩"$ .	□	□
Funkcja jest różnowartościowa.	□	□

Ćwiczenie 7

Na rysunku przedstawiono wykres funkcji $f$ .

R1ATcPASC9abo

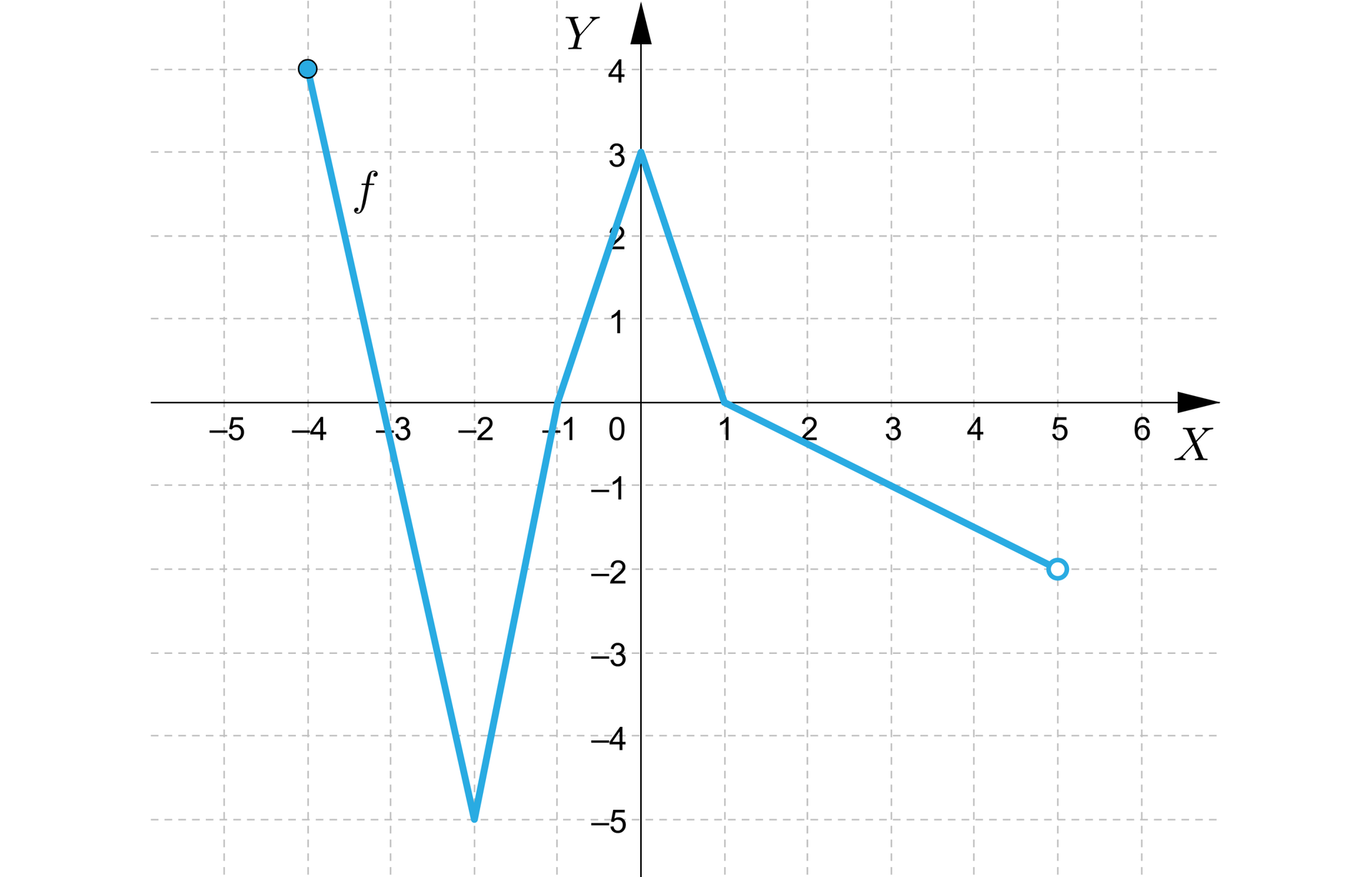
Ilustracja przedstawia układ współrzędnych z pozioma osią od minus 5 do 6 i pionową osią y od minus 5 do cztery. W układzie zaznaczono wykres funkcji f, który jest krzywą. Rozpoczyna się on w zamalowanym punkcie nawias minus cztery średnik cztery zamknięcie nawiasu, skąd biegnie ukośnie do punktu nawias minus dwa średnik minus pięć zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu o współrzędnych nawias minus jeden średnik zero zamknięcie nawiasu. Dalej biegnie ukośnie do punktu nawias zero średnik trzy zamknięcie nawiasu, skąd ukośnie biegnie do punktu o współrzędnych nawias jeden średnik zero zamknięcie nawiasu. Dalej biegnie do niezamalowanego punktu o współrzędnych nawias pięć średnik minus dwa zamknięcie nawiasu.

R1LqjlJi1hIo1

Dostępne opcje do wyboru:

⟨- 2, 0⟩

x = 1

⟨- 4, 5)

⟨0, 5)

x = - 4

x = - 2

y = - 5

(+ 1, 5)

(- 1, 1)

⟨- 4, - 2⟩

y = 4

⟨- 4, - 3)

x = - 1

⟨- 5, 4⟩

x = - 3

(- 3, - 1)

. Polecenie: Przeciągnij odpowiednie elementy, aby powstał poprawny opis własności funkcji. - dziedzina funkcji

D_{f} =

luka do uzupełnienia ,
- zbiór wartości

Z W_{f} =

luka do uzupełnienia ,
- miejsca zerowe funkcji luka do uzupełnienia , luka do uzupełnienia , luka do uzupełnienia ,
- funkcja przyjmuje wartości dodatnie dla

x \in

luka do uzupełnienia

\cup

luka do uzupełnienia ,
- funkcja przyjmuje wartości ujemne dla

x \in

luka do uzupełnienia

\cup

luka do uzupełnienia ,
- funkcja jest rosnąca w przedziale luka do uzupełnienia ,
- funkcja jest malejąca w przedziałach: luka do uzupełnienia oraz luka do uzupełnienia ,
- funkcja ma wartością najmniejszą luka do uzupełnienia dla luka do uzupełnienia , funkcja ma wartością największą luka do uzupełnienia dla luka do uzupełnienia .

Przeciągnij odpowiednie elementy, aby powstał poprawny opis własności funkcji:

$x = - 4$ , $(- 3, - 1)$ , $x = - 3$ , $"⟨"- 4, - 3")"$ , $y = 4$ , $"⟨"- 4, - 2"⟩"$ , $(+ 1, 5)$ , $(- 1, 1)$ , $"⟨"- 4, 5")"$ , $y = - 5$ , $"⟨"- 2, 0"⟩"$ , $x = - 2$ , $"⟨"- 5, 4"⟩"$ , $x = - 1$ , $x = 1$ , $"⟨"0, 5")"$

- dziedzina funkcji $D_{f} =$ ,
- zbiór wartości $Z W_{f} =$ ,
- miejsca zerowe funkcji , , ,
- funkcja przyjmuje wartości dodatnie dla $x \in$ $\cup$ ,
- funkcja przyjmuje wartości ujemne dla $x \in$ $\cup$ ,
- funkcja jest rosnąca w przedziale ,
- funkcja jest malejąca w przedziałach: oraz ,
- funkcja ma wartością najmniejszą dla , funkcja ma wartością największą dla .

Ćwiczenie 8

Na rysunku przedstawiono wykres funkcji $f$ .

R2UQQcL4Gn8bQ

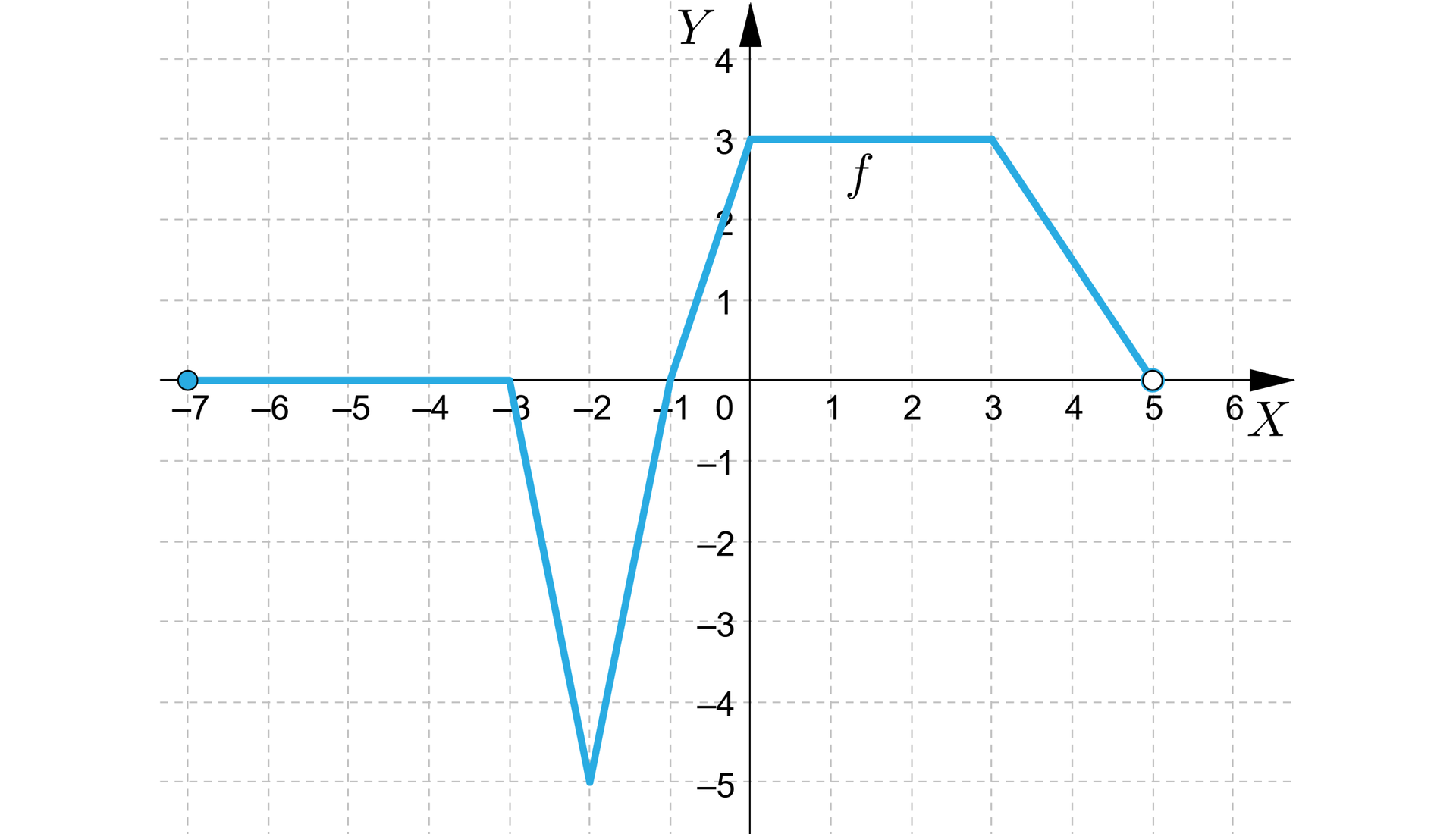
Ilustracja przedstawia układ współrzędnych z pozioma osią od minus 7 do 6 i pionową osią y od minus 5 do cztery. W układzie zaznaczono wykres funkcji f, który jest krzywą. Rozpoczyna się on w zamalowanym punkcie nawias minus siedem średnik zero zamknięcie nawiasu, skąd biegnie poziomo do punktu nawias minus trzy średnik zero zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu o współrzędnych nawias minus dwa średnik minus pięć zamknięcie nawiasu. Dalej znów biegnie ukośnie do punktu nawias minus jeden średnik zero zamknięcie nawiasu, skąd ukośnie biegnie do punktu o współrzędnych nawias zero średnik trzy zamknięcie nawiasu. Dalej biegnie poziomo do punktu o współrzędnych nawias trzy średnik trzy zamknięcie nawiasu i dalej biegnie ukośnie do niezamalowanego punktu nawias pięć średnik zero zamknięcie nawiasu.

Odczytaj z wykresu i zapisz:

dziedzinę funkcji,
zbiór wartości,
miejsca zerowe,
argumenty, dla których funkcja przyjmuje wartości ujemne,
argumenty, dla których funkcja przyjmuje wartości dodatnie,
maksymalne przedziały monotoniczności funkcji,
różnowartościowość funkcji,
najmniejszą i największą wartość funkcji oraz argumenty, dla których te wartości są przyjmowane.

$D_{f} = ⟨- 7, 5)$ ,

$Z W_{f} = ⟨- 5, 3⟩$ ,

$f (x) = 0$ dla $x \in ⟨- 7, - 3⟩ \cup \{- 1\}$ ,

$f (x) < 0$ dla $x \in (- 3, - 1)$ ,

$f (x) > 0$ dla $x \in (- 1, 5)$ ,

funkcja jest rosnąca w przedziale $⟨- 2, 0⟩$ ,
funkcja jest malejąca w przedziałach $⟨- 3, - 2⟩$ oraz $⟨3, 5)$ ,
funkcja jest stała w przedziałach $⟨- 7, - 3⟩$ oraz $⟨0, 3⟩$ ,

funkcja nie jest różnowartościowa, bo na przykład $f (0) = f (3)$ ,

wartość najmniejsza $y_{\min} = - 5$ dla $x = - 2$ ,
wartość największa funkcji $y_{\max} = 3$ dla $x \in ⟨0, 3⟩$ .

Aplet

Dla nauczyciela