Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na rysunku przedstawiony jest trójkąt prostokątny $A B C$ . Ile jest równa długość dwusiecznej $C D$ tego trójkąta?

RScTqffDSlgjJ

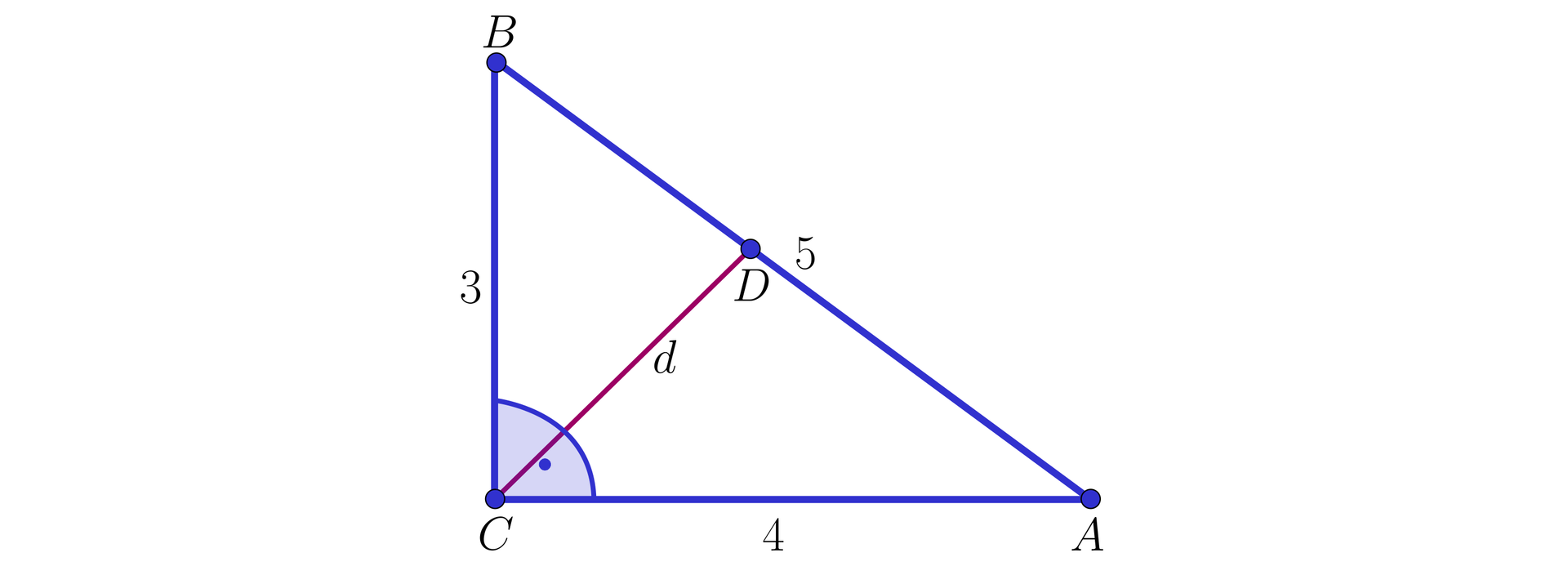
Ilustracja przedstawia trójkąt prostokątny A B C. Podstawa AC ma miarę 4 , bok CB ma miarę 3, a przeciwprostokątna długość pięć. Z wierzchołka C na przeciwprostokątną poprowadzono dwusieczną CD o mierze d.

RCUoia4LXw3hS

Zaznacz poprawną odpowiedź.

$\frac{12 \sqrt{2}}{7}$
$\frac{7 \sqrt{2}}{4}$
$\frac{5 \sqrt{2}}{3}$
$\frac{4 \sqrt{2}}{3}$

Ćwiczenie 2

Kąt ostry rombu jest równy $45 °$ . Ile jest równy stosunek długości przekątnych (dłuższej do krótszej)?

RoVXLiURjVGgo

Ilustracja przedstawia romb abcd długość krótszej przekątnej ma miarę a, a długość dłuższej ma miarę d. Kąt przy wierzchołku A wynosi 45 stopni

RDI1PZgfxGEJY

Zaznacz poprawną odpowiedź.

$\frac{2 + \sqrt{2}}{2 - \sqrt{2}}$
$\frac{\sqrt{2} + 1}{\sqrt{2} - 1}$
$\frac{2 \sqrt{2} + 1}{2 \sqrt{2} - 1}$
$\frac{2}{\sqrt{2}}$

Ćwiczenie 3

Punkt $D$ dzieli bok $A B$ trójkąta $A B C$ na odcinki $A D$ i $B D$ o długościach $4$ i $5$ , a boki $A C$ i $B C$ tego trójkąta mają długości $8$ i $7$ , jak na rysunku.

RpTZP9vA7tbaF

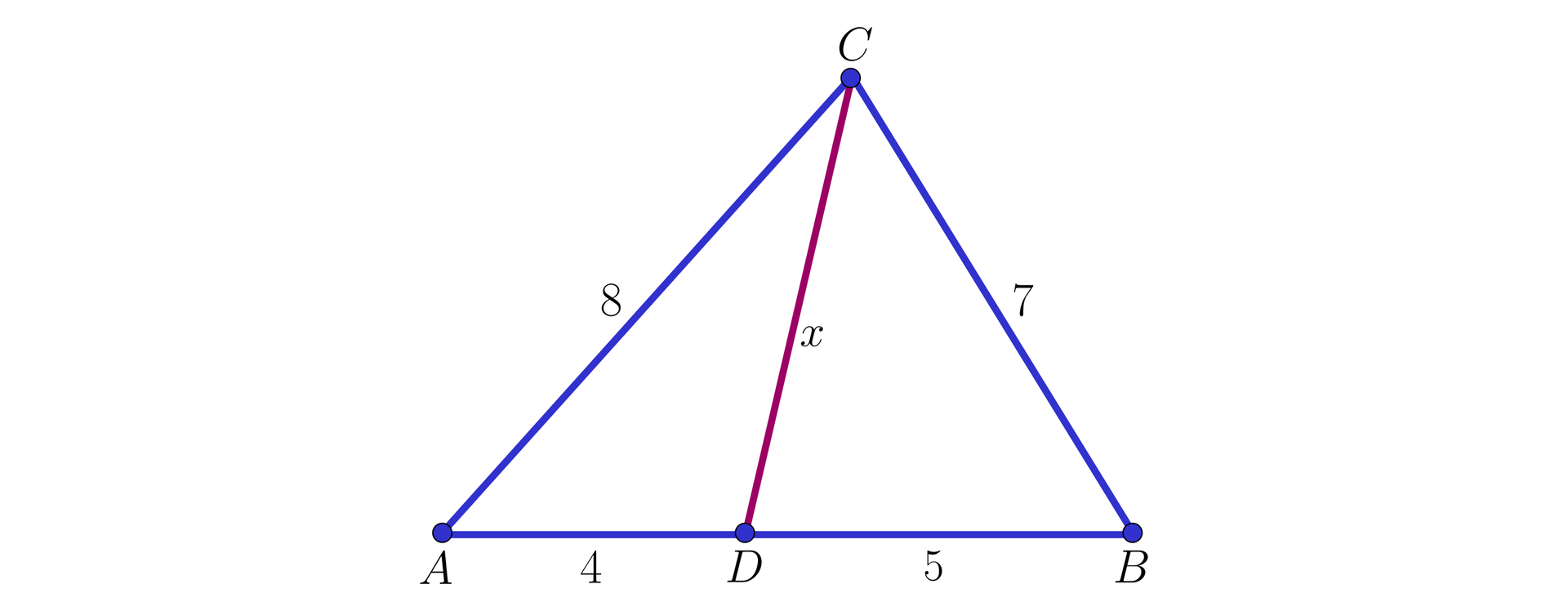
Ilustracja przedstawia trójkąt ABC, długość boku AC ma miarę 8, a długość boku BC ma miarę 7 z wierzchołka C poprowadzono prostą x na podstawę tworząc punkt D, który dzieli podstawę AB na odcinki AD równe 4 oraz BD równe 5

RKYHFh3yRAYxB

Dokończ zdanie przeciągając poprawną odpowiedź.

$\sqrt{56}$ , $\frac{4 \sqrt{21}}{3}$ , $\frac{68}{9}$ , $6$

Długość $x$ odcinka $C D$ jest równa .

Ćwiczenie 4

Boki trójkąta $A B C$ mają długości równe $|A B| = c$ , $|B C| = a$ i $|A C| = b$ . Punkt $D$ dzieli bok $A B$ trójkąta $A B C$ na odcinki $A D$ i $B D$ w stosunku $|A D| : |B D| = 1 : 2$ .

R1XZ5bgsJuNJW

Ilustracja przedstawia trójkąt ABC, długość boku AC ma miarę b, a długość boku BC ma miarę c z wierzchołka C poprowadzono prostą x na podstawę tworząc punkt D, który dzieli podstawę AB o długości c na odcinki AD oraz BD.

R1adtTfajAG7i

Wstaw brakującą liczbę tak, żeby otrzymać równość prawdziwą.

$3 a^{2} + 6 b^{2} =$ ............ $\cdot x^{2} + 2 c^{2}$

Ćwiczenie 5

Udowodnij, że jeżeli długości $a$ , $b$ , $c$ boków trójkąta $A B C$ spełniają równanie $\frac{a}{b + c} + \frac{c}{a + b} = 1$ , to kąt tego trójkąta między bokami o długościach $a$ i $c$ jest równy $60 °$ .

Przyjmijmy standardowe oznaczenia w trójkącie. Musimy wykazać, że $β = 60 °$ . Mnożąc obie strony równości $\frac{a}{b + c} + \frac{c}{a + b} = 1$ przez $(b + c) (a + b)$ , otrzymujemy równość równoważną
$a (a + b) + c (b + c) = (a + b) (b + c)$ . Stąd mamy $a^{2} + a b + b c + c^{2} = a b + a c + b^{2} + b c$ , czyli $a^{2} + c^{2} = b^{2} + a c$ .
Z twierdzenia cosinusów wiemy, że $b^{2} = a^{2} + c^{2} - 2 a c \cos β$ , więc otrzymaną równość możemy zapisać w postaci $a^{2} + c^{2} = a^{2} + c^{2} - 2 a c \cos β + a c$ .
Stąd dostajemy $2 a c \cos β = a c$ , skąd $\cos β = \frac{a c}{2 a c} = \frac{1}{2}$ . Ponieważ $β$ jest kątem trójkąta, więc $β = 60 °$ .
To kończy dowód.

Ćwiczenie 6

Długości dwóch sąsiednich boków równoległoboku $A B C D$ są równe $a$ i $b$ , a długości przekątnych tego równoległoboku są równe $c$ i $d$ .

R1WAWvUtK8xio

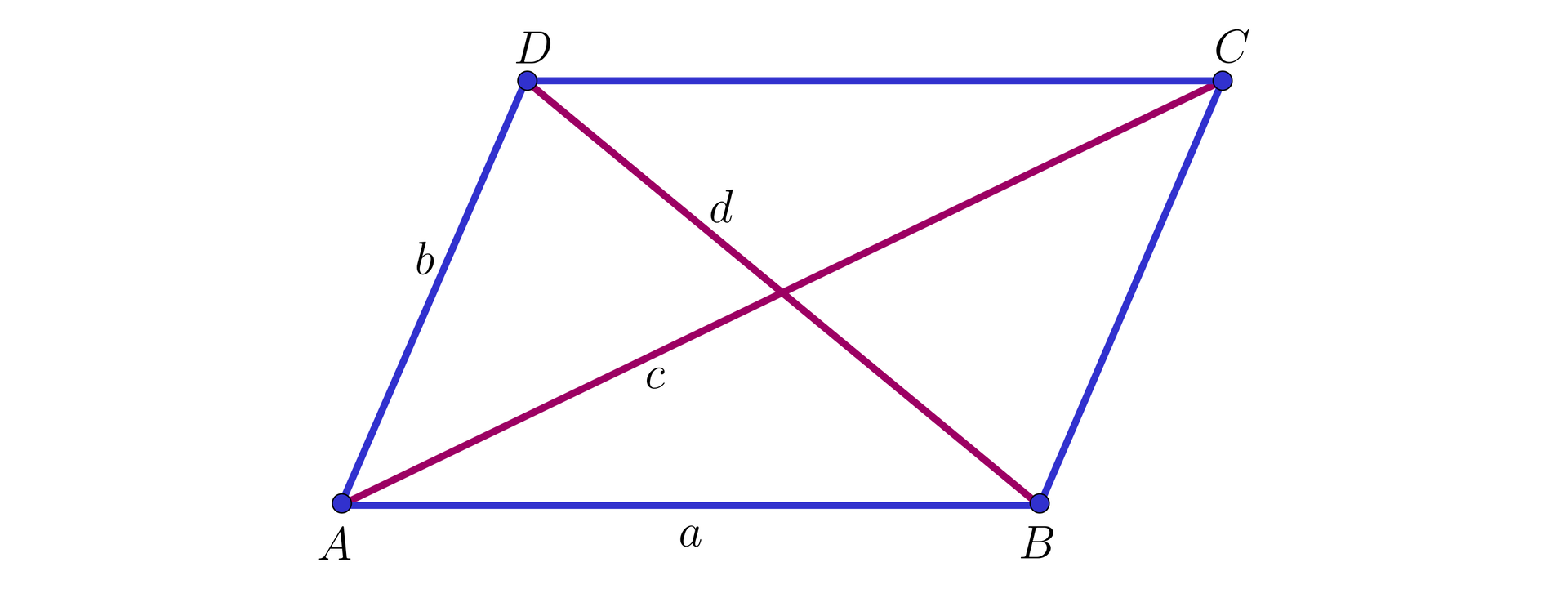
Ilustracja przedstawia równoległobok A B C D, w którym długości dwóch sąsiednich boków są równe a i b, a długości przekątnych tego równoległoboku są równe c i d.

Udowodnij, że $c^{2} + d^{2} = 2 a^{2} + 2 b^{2}$ .

Niech $|∢ B A D| = α$ . Wtedy $|∢ A B C| = 180 ° - α$ .

Rw8GhYQwSsW8O

Z twierdzenia cosinusów zastosowanego dla kąta $α$ w trójkącie $A B D$ i dla kąta $180 ° - α$ w trójkącie $A B C$ otrzymujmy
$d^{2} = a^{2} + b^{2} - 2 a b \cos α$ oraz $c^{2} = a^{2} + b^{2} - 2 a b \cos (180 ° - α)$ .
Ponieważ $\cos (180 ° - α) = - \cos α$ , więc możemy ten układ równań zapisać w postaci
$d^{2} = a^{2} + b^{2} - 2 a b \cos α$ oraz $c^{2} = a^{2} + b^{2} + 2 a b \cos α$ .
Sumując stronami otrzymane równości, otrzymujemy
$c^{2} + d^{2} = 2 a^{2} + 2 b^{2}$
To kończy dowód.

Ćwiczenie 7

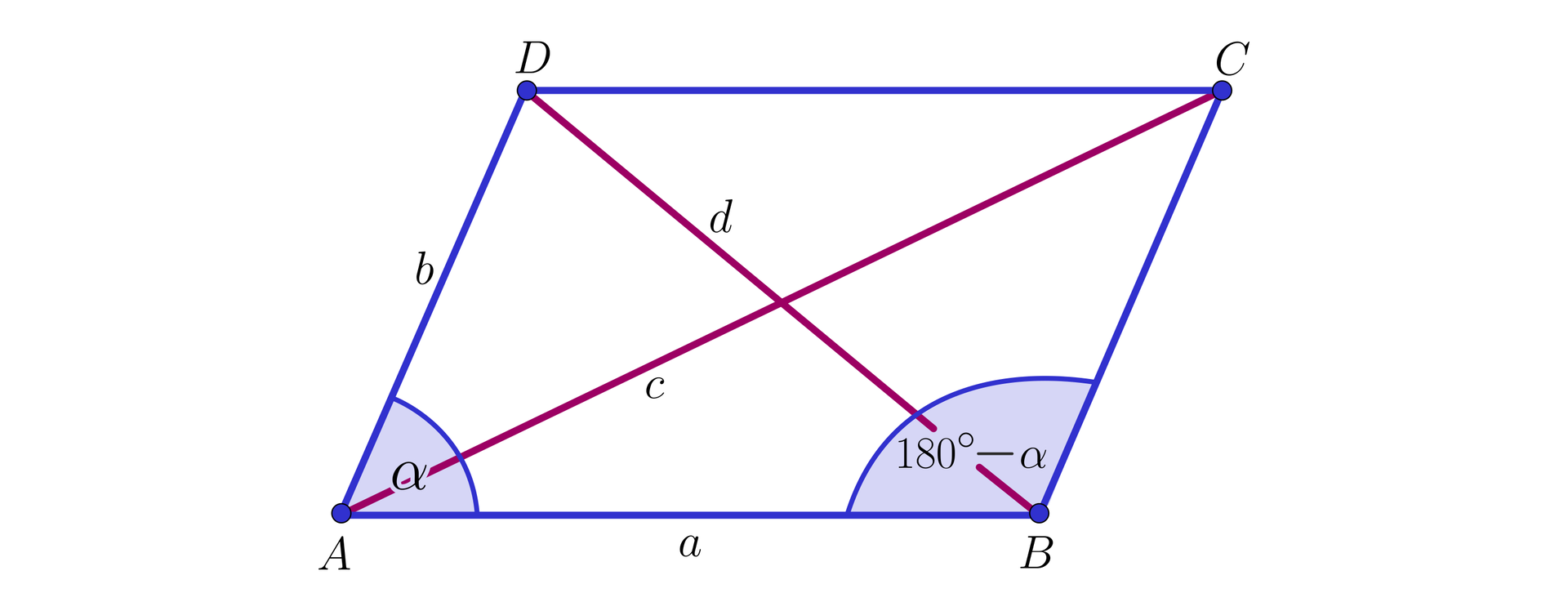
Czworokąt $A B C D$ o bokach długości $a$ , $b$ , $c$ , $d$ jest wpisany w okrąg, a jego przekątne mają długości $m$ i $n$ , jak na rysunku.

RXhVhKK9u8FPB

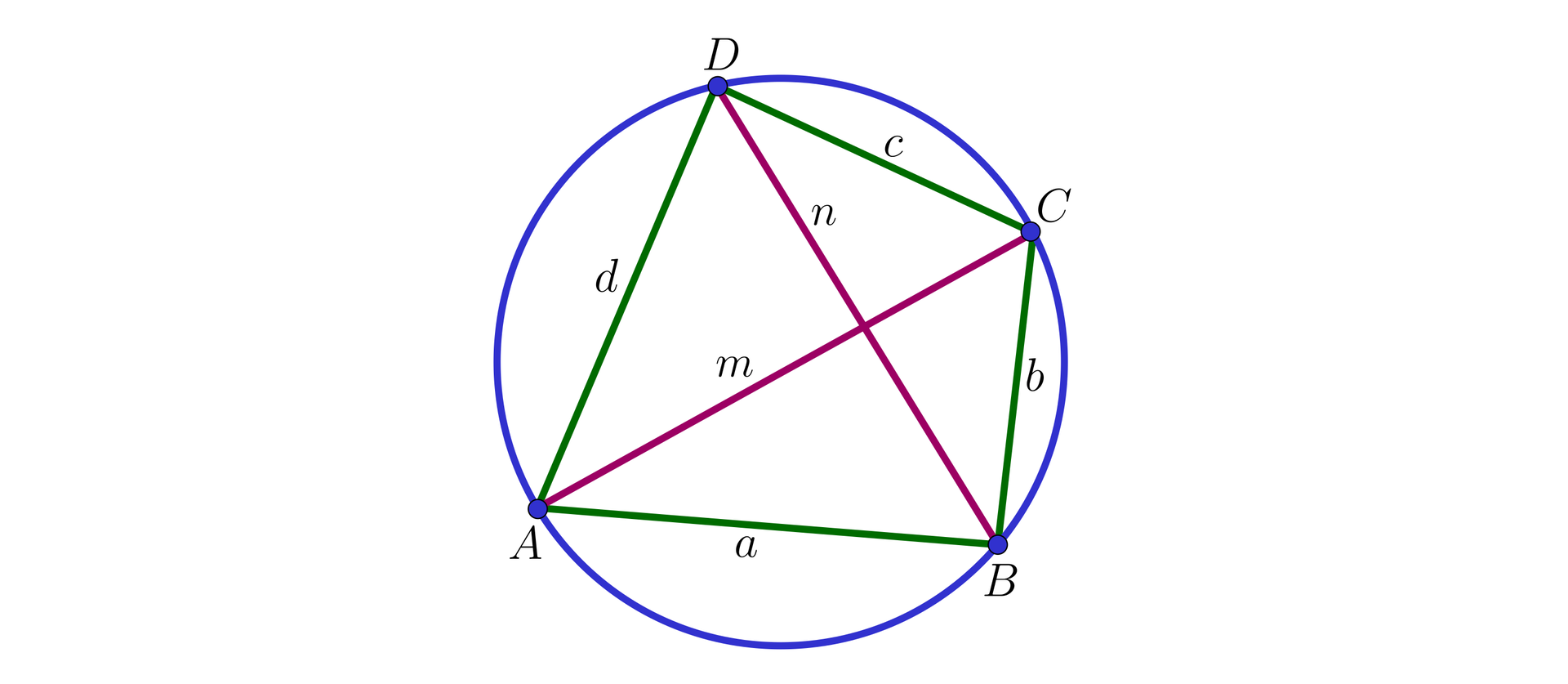
ilustracja przedstawia czworokąt abcd o bokach długości a,b,c,d wpisanych w okrąg. Jego przekątne mają długości m i n.

Udowodnij, że długość przekątnej tego czworokąta wyraża się wzorem
$m = \sqrt{\frac{(a d + b c) (a c + b d)}{a b + c d}}$ .

Niech $|∢ A B C| = β$ . Wtedy $|∢ A D C| = 180 ° - β$ , gdyż czworokąt $A B C D$ jest wpisany w okrąg.

RwMv7xsPxkOGT

ilustracja przedstawia czworokąt abcd o bokach długości a,b,c,d wpisanych w okrąg. Jego przekątne mają długości m i n. kąt przy wierzchołku B ma miarę beta, a kąt przy wierzchołku D ma miarę 180°-β

Z twierdzenia cosinusów zastosowanego dla kąta $β$ w trójkącie $A B C$ i dla kąta $180 ° - β$ w trójkącie $A D C$ otrzymujmy
$m^{2} = a^{2} + b^{2} - 2 a b \cos β$ oraz $m^{2} = c^{2} + d^{2} - 2 c d \cos (180 ° - β)$ .
Ponieważ $\cos (180 ° - β) = - \cos β$ , więc możemy ten układ równań zapisać w postaci
$m^{2} = a^{2} + b^{2} - 2 a b \cos β$ oraz $m^{2} = c^{2} + d^{2} + 2 c d \cos β$ .
Mnożąc obie strony pierwszego równania przez $c d$ , a drugiego przez $a b$ , otrzymujemy
$c d m^{2} = c d a^{2} + c d b^{2} - 2 a b c d \cos β$ oraz $a b m^{2} = a b c^{2} + a b d^{2} + 2 a b c d \cos β$ .
Stąd, po zsumowaniu tych równań stronami, otrzymujemy
$a b m^{2} + c d m^{2} = a b c^{2} + a b d^{2} + c d a^{2} + c d b^{2}$ ,
$(a b + c d) m^{2} = a c \cdot b c + a d \cdot b d + a c \cdot a d + b c \cdot b d$ ,
$(a b + c d) m^{2} = a c (b c + a d) + b d (a d + b c)$ ,
$m^{2} = \frac{(a d + b c) (a c + b d)}{a b + c d}$ .
Stąd $m = \sqrt{\frac{(a d + b c) (a c + b d)}{a b + c d}}$ .
To kończy dowód.

Ćwiczenie 8

Udowodnij twierdzenie Ptolemeusza:

W czworokącie wpisanym w okrąg iloczyn długości przekątnych jest równy sumie iloczynów długości przeciwległych boków. Przy oznaczeniach jak na rysunku

RvTqRFoCXWeR9

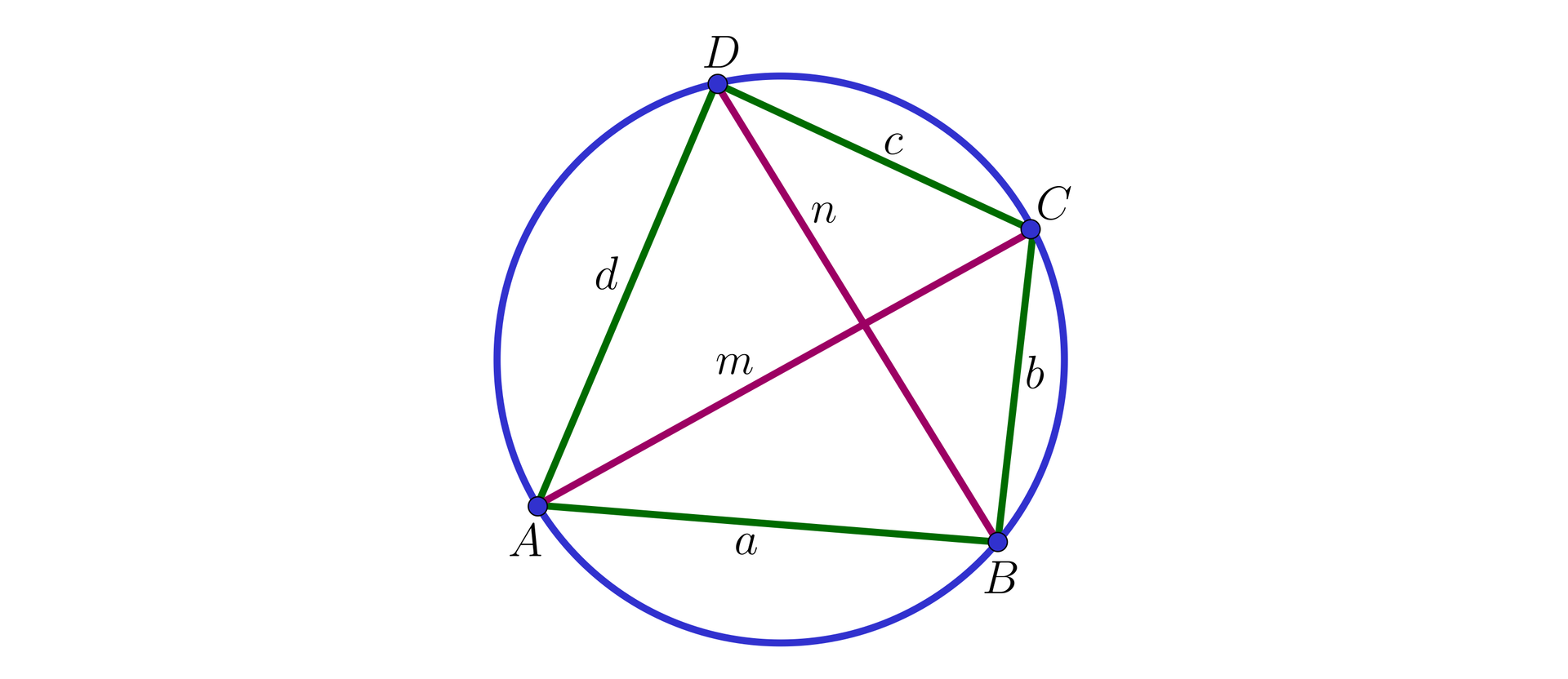
teza tego twierdzenia ma postać

$m n = a c + b d$ .

W dowodzie wykorzystaj wzór na długość przekątnej czworokąta wpisanego w okrąg z Ćwiczenia 7.

Przekątne czworokąta $A B C D$ o bokach długości $a$ , $b$ , $c$ , $d$ wpisanego w okrąg są równe
$m = \sqrt{\frac{(a d + b c) (a c + b d)}{a b + c d}}$ oraz $n = \sqrt{\frac{(a b + c d) (a c + b d)}{a d + b c}}$ .
Zatem
$m n = \sqrt{\frac{(a d + b c) (a c + b d)}{a b + c d}} \cdot \sqrt{\frac{(a b + c d) (a c + b d)}{a d + b c}} = \sqrt{\frac{(a d + b c) (a c + b d)}{a b + c d} \cdot \frac{(a b + c d) (a c + b d)}{a d + b c}} =$
$= \sqrt{{(a c + b d)}^{2}} = a c + b d$ .
To kończy dowód.

Animacja

Dla nauczyciela