Sprawdź się

Pokaż ćwiczenia:

RL3vHuJW8lQmz1

Ćwiczenie 1

Dziedziną funkcji $f$ jest zbiór $"{"- 3, - 2, 0, 1, 4"}"$ . Określamy funkcję $g (x) = f (- x)$ . Przyporządkuj liczby zgodnie z podanymi opisami.

Należą do dziedziny funkcji $g$ :
Nie należą do dziedziny funkcji $g$ :

ROijcPq3skQVq1

Ćwiczenie 2

Funkcja $f$ jest określona przez zbiór par $"{"(- 2, 4), (- 1, 5), (2, 3), (5, 0)"}"$ . Określamy funkcję $g$ wzorem $g (x) = f (- x)$ . Wówczas funkcja $g$ jest określona przez zbiór złożony z par:

$- 2$ , $- 1$ , $2$ , $5$ , $0$ , $- 5$ , $1$

$($ ............, $4)$ , $($ ............, $5)$ , $($ ............, $3)$ , $($ ............, $0)$ .

RRDDIAo0TL7DC2

Ćwiczenie 3

Dziedziną funkcji $f$ jest przedział $"("- 2, 3"⟩"$ . Określamy funkcję $g$ wzorem $g (x) = f (- x)$ . Dziedziną funkcji $g$ jest przedział:

$"⟨"- 3, 2")"$
$"("- 2, 3"⟩"$
$"⟨"- 2, 3")"$

Ćwiczenie 4

Na rysunku przedstawiono wykres funkcji $f$ określonej dla liczb nie mniejszych od $2$ .

RG27dKe7Grfdp

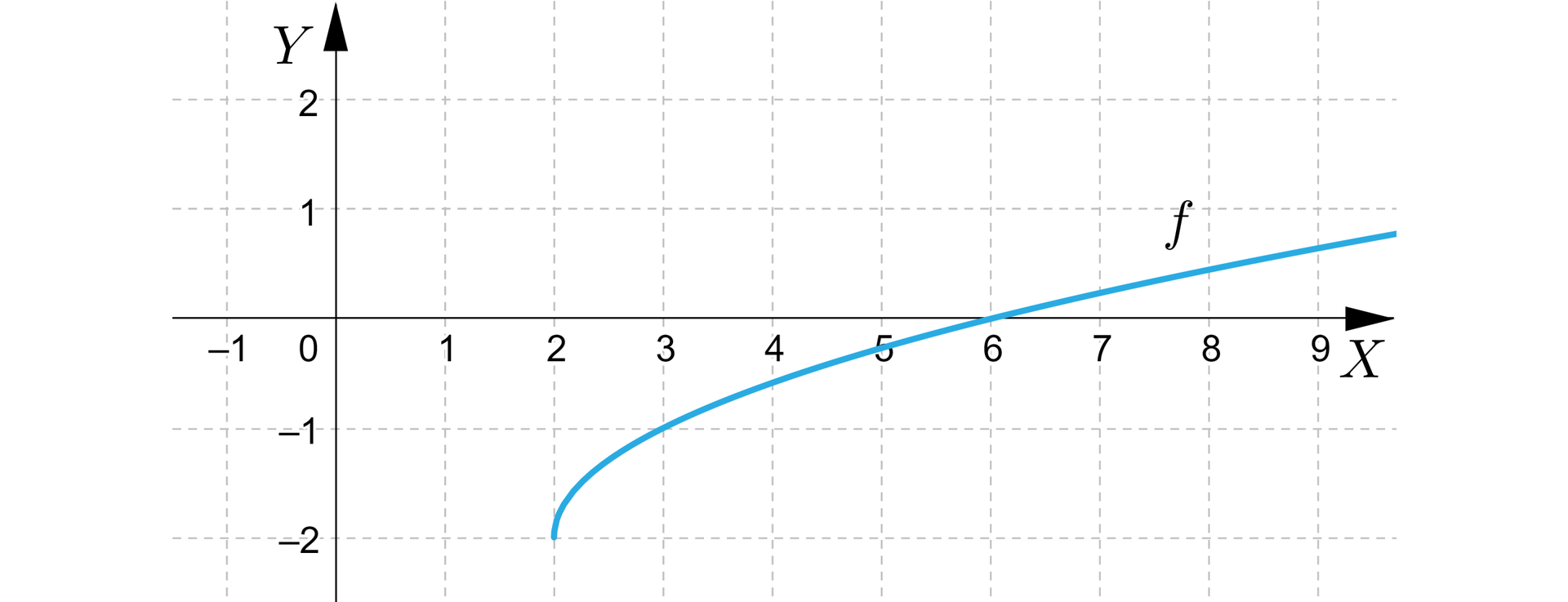
Ilustracja przedstawia układ współrzędnych z osią pionową Y od minus dwóch do dwóch oraz osią poziomą od minus 1 do dziewięciu. Zaznaczono wykres funkcji f zaczynający się od punktu 2;-2 rosnący do nieskończoności.

RlzieSQcX3EL9

Dziedziną funkcji określonej wzorem $g (x) = f (- x)$
jest przedział $(- \infty,$ ............ $⟩$ .
Zbiorem wartości funkcji określonej wzorem $g (x) = f (- x)$
jest przedział $⟨$ ............ $, \infty)$ .

R1NfrvVxrtouU2

Ćwiczenie 5

Uzupełnij:

$- 3$ , $- 4$ , $3$ , $4$ , $0$

Wiadomo, że $f (4) = 0$ oraz $f (0) = 3$ . Jeśli wykres funkcji $g$ jest symetryczny do wykresu funkcji $f$ względem osi $Y$ , to
$g (- 4) =$ ............,
$g (0) =$ .............

RPGTMvKzbS85n2

Ćwiczenie 6

Dana jest funkcja $f$ ; określamy funkcję $g$ wzorem $g (x) = f (- x)$ . Dopasuj wzór funkcji $g$ do wzoru funkcji $f$ , jeśli

$f (x) = x^{2} + 1$ , $f (x) = x^{3} + 1$ , $f (x) = \frac{x}{x + 1}$ , $f (x) = \frac{- x}{x - 1}$ , $g (x) = - x^{2} + 1$ , $g (x) = x^{3} - 1$ , $g (x) = \frac{x}{x + 1}$

$f$	$g$
$f (x) = x^{2} + 1$
$f (x) = x^{3} + 1$
$f (x) = \frac{x}{x + 1}$
$f (x) = \frac{- x}{x - 1}$

R1HG30QuyY3cf3

Ćwiczenie 7

Wykres funkcji $g$ jest symetryczny do wykresu funkcji $f$ w symetrii względem osi $Y$ . Wówczas:

funkcje mają te same zbiory wartości
wykresy funkcji są symetryczne względem prostej $y = 0$
funkcje mają te same dziedziny
funkcje mają jednakowe miejsca zerowe

Ćwiczenie 8

Na rysunku przedstawiono wykres funkcji $f$ .

RzdOuxv9EeeE0

Ilustracja przedstawia układ współrzędnych z osią pionową Y od minus 1 do sześciu oraz osią poziomą od minus 5 do pięciu. Zaznaczono parabolę z ramionami skierowanymi w górę oraz wierzchołkiem odbitym względem osi X. znajduję się on teraz w pierwszej ćwiartce.

RjB6KnhlUAXAW

Wykres funkcji $g$ jest symetryczny do wykresu funkcji $f$ z rysunku.

$- 8$ , $- 28$ , $28$

Wartość wyrażenia $9 g (- 1) + 12 g (0) - g (- 3)$ wynosi .............

Aplet

Dla nauczyciela